Vocking B., Alt H., Dietzfelbinger M., Reischuk R., Scheideler C., Vollmer H., Wagner D. Algorithms Unplugged

Подождите немного. Документ загружается.

270 Sigrid Knust

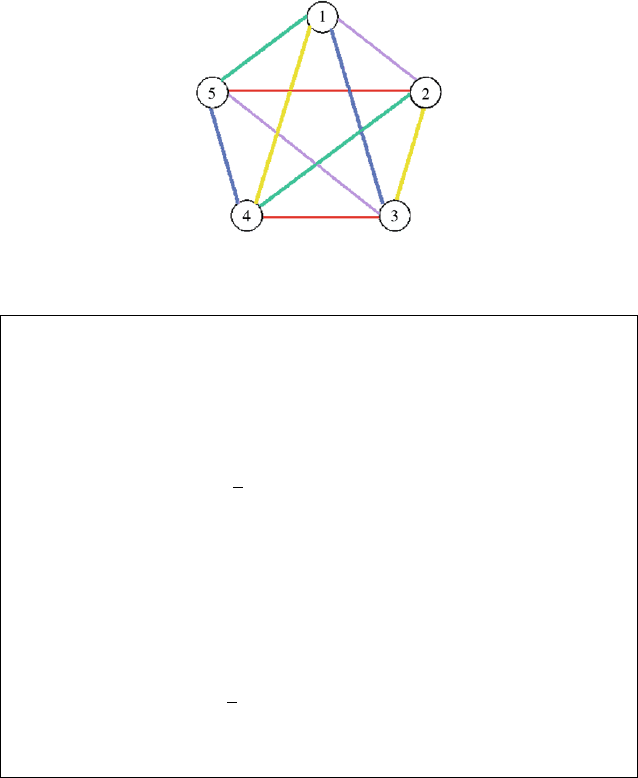
Fig. 27.3. Resulting pentagon

Algorithm Edge Coloring (geometrical version):

1. Build a regular polygon from the vertices 1, 2,...,n−1 and place

the vertex n to the top left side beside the polygon.

2. Connect vertex n with the “top” of the polygon.

3. Connect each of the remaining vertices with the opposite vertex

on the same height in the polygon.

4. Color the resulting

edges with the ﬁrst color (in the example

we color the edges 6-1, 5-2, 4-3).

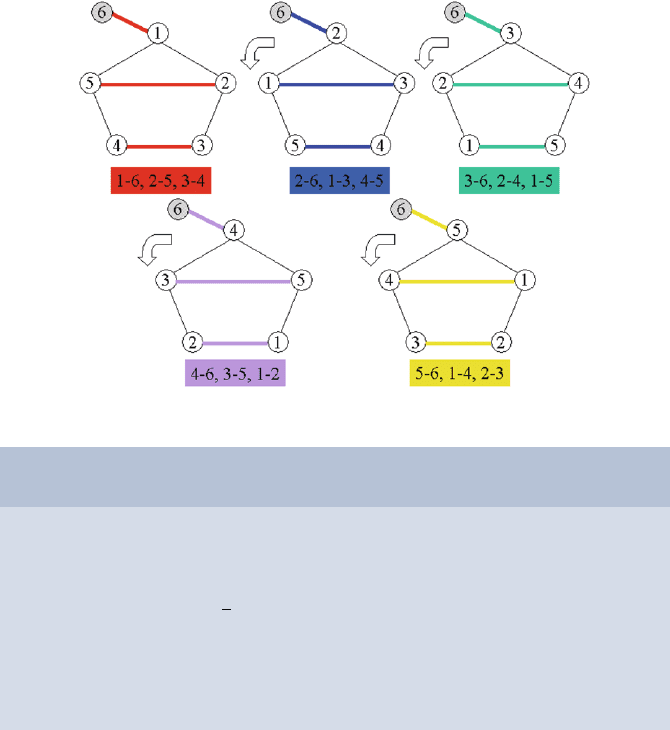
5. Rotate the vertices 1,...,n− 1 of the polygon cyclically anti-

clockwise by one position (i.e., vertex 2 is moved to the position

of vertex 1, vertex 3 replaces the old vertex 2, ..., vertex n − 1

replaces the old vertex n −2 and vertex 1 replaces the old vertex

n −1). Vertex n stays at the same place beside the polygon, and

the edges added in Steps 2 and 3 remain at their positions in the

polygon.

6. Color the resulting

edges with the second color (in the example

we color the edges 6-2, 1-3, 5-4).

7. Repeat Steps 5 and 6 for the remaining colors 3,...,n− 1.

of parallel edges in n − 1 iterations (see also Fig. 27.4). It can be shown that

this algorithm generates a feasible edge coloring for any even number n.

In order to implement the algorithm presented above using a computer, it

would be relatively costly to store polygons and rotate them cyclically in each

iteration. Using the division of integers with remainder (modulo operation,

see Chap. 12), the algorithm can simply be written as follows:

27 Scheduling of Tournaments or Sports Leagues 271

Fig. 27.4. Iterations of the procedure

The algorithm ColorEdges colors all edges of the complete graph with an

even number n of vertices with n − 1 colors.

1 procedure ColorEdges (n)

2 begin

3 for all colors i := 1 to n − 1 do

4 color edge [i, n] with color i

5 for k := 1 to

− 1

6 color all edges [(i + k)mod(n − 1), (i − k)mod(n − 1)]

7 with color i

8 endfor

9 endfor

10 end

In this algorithm a mod b denotes the remainder after dividing the integer

a by the integer b. For example,

• 14 mod 4 = 2, since 14 = 3 · 4+2,

• 9mod3=0, since 9=3·3+0and

•−1mod5= 4, since −1=(−1) · 5+4.

If we divide by the number n − 1 in Step 6, we get remainders from the set

0, 1,...,n− 2. Since our vertices are numbered by 1,...,n− 1 (and not by

0, 1,...,n−2), we identify the remainder 0 with n − 1.

In our example in Step 6 we get for i = 1 the edges

• [(1 + 1) mod 5, (1 − 1) mod 5] = [2, 5] for k =1,and

• [(1 + 2) mod 5, (1 − 2) mod 5] = [3, 4] for k =2.

The calculation of the values for i =2, 3, 4, 5 may be done by the reader.

272 Sigrid Knust

Schedules with Home–Away Assignments

Let us again consider a soccer league. In contrast to the table-tennis tourna-

ment, the matches are not performed at the same location, but in the stadi-

ums of the teams. If in the ﬁrst half series the match between teams i and j

is scheduled in the stadium of team i, then in the second half series team j

is the home team. Thus, in a schedule for such a league, in addition to the

pairings (who plays whom) per round, for each pairing a home team has to

be determined.

For various reasons (e.g., fairness, attractiveness for the spectators) for

each team home and away matches should alternate as much as possible. If a

team has two consecutive home or away matches, this is also called a break

(the alternating sequence of H- and A-matches is broken). When breaks are

undesirable, a schedule without any breaks would be the best. But, if we have

a closer look at the schedules of diﬀerent leagues in various sports disciplines

we see that in every season breaks occur. We may ask the question whether

breaks are unavoidable or whether better schedules (without any breaks) exist.

It is relatively easy to see that with respect to our constraints no schedule

without any breaks exists. If no team has a break, each team must have a

home–away sequence of the form HAHA. . . H or AHAH...A. On the other

hand, two teams with the same home–away sequence (e.g., HAHA. . . H) can

never play against each other (since always both teams play either home or

away). For this reason at most two teams can have a home–away sequence

without any break. Thus, the remaining n − 2 teams must have at least one

break, i.e., each schedule for a half series contains at least n − 2 breaks.

It can be shown that schedules with exactly n − 2 breaks exist which

can be generated with an extension of the algorithm described above. In this

extension additionally the home team has to be determined in Steps 4 and 6

of algorithm ColorEdges as follows:

• Any match [i, n] is a home match for team i if i is even; otherwise it is a

home match for team n.

• Any match [(i + k)mod(n − 1), (i − k)mod(n − 1)] is a home match for

team (i + k)mod(n −1) if k is odd; otherwise it is a home match for team

(i − k)mod(n − 1).

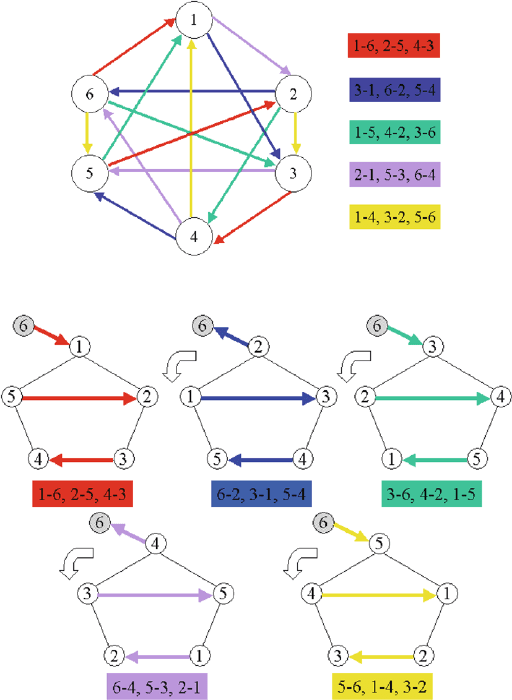
In our graph model, home and away matches can easily be integrated if the

edges are oriented. If the directed arc i → j means that the match between

teams i and j takes place at team j, then for our example with n = 6 teams,

using the extended algorithm we obtain the schedule from Fig. 27.5 with

n − 2

= 4 breaks (teams 1 and 6 have no break, teams 2, 3, 4, 5 each have

one break).

The

geometrical construction procedure based on the polygon can also be

extended by giving each edge an orientation. While the edges in the polygon

are always oriented in the same direction, the orientation of the edge to the

outer vertex n alternates in each iteration (see Fig. 27.6).

27 Scheduling of Tournaments or Sports Leagues 273

Fig. 27.5. Schedule with n − 2breaks

Fig. 27.6. Iterations of the extended procedure

Summarizing, we can state that for any even number n of teams a schedule

with n − 1 rounds and n − 2 breaks exists which can be constructed by the

described algorithm.

Finally, let us come back to the soccer league. Since there we have two

half series, in each half series at least n − 2 breaks occur. In the professional

German soccer league the matches of the second half series are scheduled in

the same sequence as in the ﬁrst half series (with exchanged home rights). For

such a system it can be shown that at least 3n − 6 breaks occur. A schedule

having 3n−6 breaks (n−2 in both half series and n −2 at the border between

ﬁrst and second half series) can easily be constructed with the above method.

Using a slight modiﬁcation, it can additionally be ensured that no team has

two consecutive breaks.

274 Sigrid Knust

Usually, scheduling of a sports league in practice is more diﬃcult since

additional constraints have to be respected. For example, if a league contains

teams which share the same stadium, two such teams cannot play at home

simultaneously. Thus, when one of these teams plays at home, the other must

play away. Furthermore, due to limited train or police capacities, not too

many matches should be played in a region at the same day. Additionally, it

may happen that in some rounds a stadium is unavailable since another event

(e.g., a concert or a fair) is already taking place. Then the corresponding team

has to play away in such a round. Finally, the media and spectators expect

a varied, eventful, and exciting season (e.g., top matches should be scheduled

at the end of a season) and attractive matches should be distributed evenly

over the season.

For now most sports leagues schedules are still constructed manually.

A scheduler generates a generic schedule for the corresponding league size

with the above algorithm where at ﬁrst the numbers 1,...,n are used as

placeholders for the teams. Afterwards, in a second step each speciﬁc team

is assigned to a number (e.g., 1 = Werder Bremen, 2 = Hamburger SV, 3 =

Bayern M¨unchen, etc.). In this step as many additional constraints are met as

possible (e.g., that two teams sharing the same stadium never play at home

simultaneously).

Let us now consider how many diﬀerent team assignments are possible for

a league with n = 18 teams. For the ﬁrst number we can choose among 18

teams, and for the second number we have 17 possible teams (since the ﬁrst

team is already chosen), then 16 possibilities for the third number, etc. Thus,

in total we get 18! = 18 · 17 · 16 ···· ·2 · 1 ≈ 6.4 · 10

possibilities. If we

assume that a computer can generate 10

solutions per second, we need 74

days in order to check all possibilities. This enormously huge number shows

that a human scheduler even with the help of a computer can only check a

very small number of possible schedules.

A further disadvantage of the described method is that only one speciﬁc

schedule is used as the foundation for the assignment. There are several other

schedules which cannot be generated with the above method. Thus, with

this procedure it cannot be guaranteed that good schedules (i.e., schedules

satisfying the given constraints as much as possible) are found. For this reason,

current research in the area of sports scheduling deals with the development

of new algorithms that try to calculate good schedules in a reasonable amount

of time.

Further Reading

1. Chapter 28 (Eulerian Circuits), Chap. 32 (Shortest Paths), Chap. 33 (Min-

imum Spanning Trees), Chap. 34 (Maximum Flows) and Chap. 40 (The

Travelling Salesman Problem).

27 Scheduling of Tournaments or Sports Leagues 275

Further models and algorithms based on graphs can be found in these

chapters.

2. J.M. Aldous and R.J. Wilson: Graphs and Applications. Springer, 2003.

An introduction to graphs and their applications.

3. Eric W. Weisstein: Kirkman’s Schoolgirl Problem. From MathWorld –

A Wolfram Web Resource:

http://mathworld.wolfram.com/KirkmansSchoolgirlProblem.html

An additional combinatorial problem where solutions can be represented

by graph colorings.

4. S. Knust: Construction Methods for Sports League Schedules

http://www.informatik.uos.de/knust/sportssched/webapp/index.

html

A website where diﬀerent construction methods for sports league schedules

are shown (e.g., the construction methods discussed above).

Eulerian Circuits

Michael Behrisch, Amin Coja-Oghlan, and Peter Liske

Humboldt-Universit¨at zu Berlin, Berlin, Germany

University of Warwick, Coventry, UK

Humboldt-Universit¨at zu Berlin, Berlin, Germany

Teasing your mates with riddles can be quite an amusing pastime

– provided that you know the answer already! The “House of

Santa Claus” provides a nice little teaser:

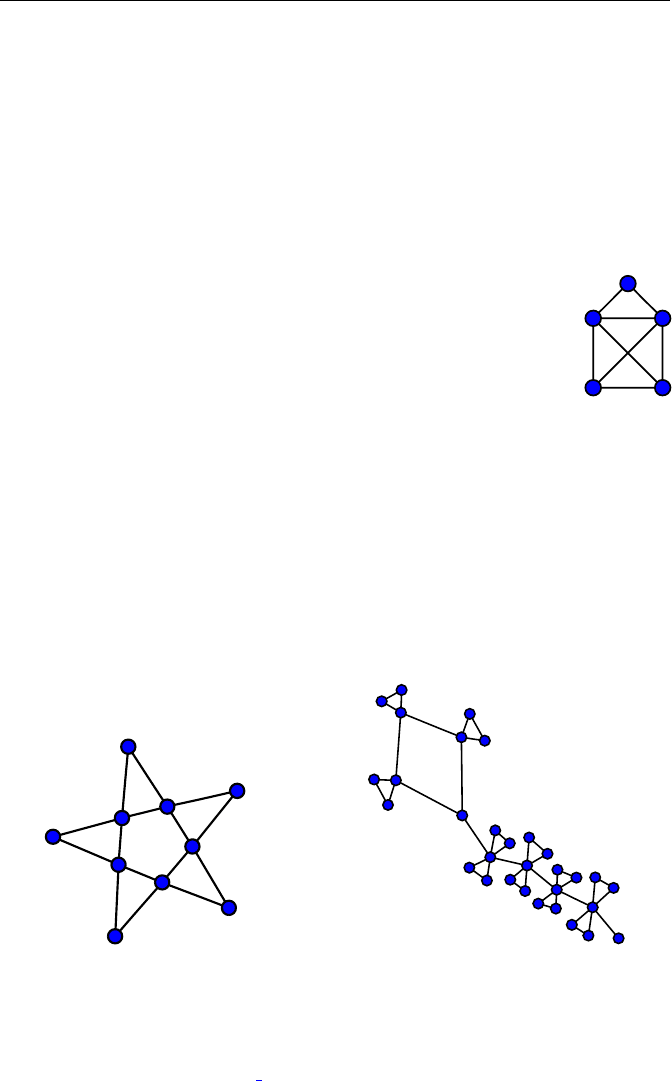
This ﬁgure consists of ﬁve nodes (the blue dots) and eight

edges (the lines that connect the nodes). Can you draw the House

of Santa Claus in one sweep, without lifting the pen and without

drawing any edge twice?

Of course, it won’t be long until all your friends know how to solve this

one (as there are actually 44 diﬀerent ways of drawing the House of Santa

Claus). But fortunately there are plenty of other ﬁgures that can be drawn in

one sweep as well, provided that you know how. In some other cases you may

end up trying for quite a while, just to realize that drawing the ﬁgure in one

go seems all but impossible.

In this chapter we present an algorithm that will always produce a way to

draw a given ﬁgure in one go if this is possible. To devise such an algorithm,

let us ﬁrst try to deal with ﬁgures that can be drawn in one sweep such that

Fig. 28.1. Try the star and the dragon!

B. V¨ocking et al. (eds.), Algorithms Unplugged,

DOI 10.1007/978-3-642-15328-0

28,

 Springer-Verlag Berlin Heidelberg 2011

278 Michael Behrisch, Amin Coja-Oghlan, and Peter Liske

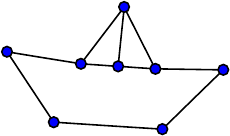
Fig. 28.2. The sailing boat provides a counterexample

the pen ends up at the same node where it started. The route that the pen

traverses is then called an Eulerian circuit. This is because the mathemati-

cian Leonhard Euler was the ﬁrst to ﬁnd out what ﬁgures can be sketched

in this way. (Actually Leonhard Euler was mostly interested in one partic-

ular ﬁgure, namely the roadmap of his home town of K¨onigsberg.) Follow-

ing Euler, we ﬁrst deal with the question of whether an Eulerian circuit ex-

ists. Later on we sort out how to ﬁnd an Eulerian circuit quickly if there is

one.

In what follows we are going to ﬁgure out why, for example, the star has

an Eulerian circuit, and why neither the House of Santa Claus nor the ship

admit one. Bizarrely, the House of Santa Claus can be drawn in one go if we

allow that the pen ends up at a diﬀerent node than where it started, whereas

even this is impossible in the case of the ship. To ﬁnd out why, we need to take

acloserlookatthenodes, i.e., the places where the pen can change direction.

(Recall that the nodes are just the blue dots in our ﬁgures.)

When Does an Eulerian Circuit Exist?

The degree of a node is the number of edges that pass through that node. For

instance, the degree of the mast top of the ship is three. If we draw a ﬁgure

in one sweep so that in the end the pen returns to the starting point, then

the pen leaves every vertex exactly as many times as it enters that vertex. In

eﬀect, the degree of each node is even.

Observe that the ship has four nodes of odd degree (namely, all the nodes

that belong to the sail). This shows that it is impossible to draw the ship in

one go such that the starting point and the endpoint coincide. The same is

true of the House of Santa Claus, because it has two nodes of degree three.

However, there is a little twist (to be revealed later) that enables us to draw

the ﬁgure in one sweep, but with diﬀerent starting point and endpoint. By

contrast, all nodes of the star have even degree. But does any ﬁgure with

this property feature an Eulerian circuit? And, if so, how do we actually ﬁnd

one?

28 Eulerian Circuits 279

Finding Eulerian Circuits

Suppose that all nodes have even degrees. In the absence of a better idea,

we could just start somewhere and go ahead drawing.Thatis,westartatan

arbitrary node and follow an arbitrary edge to another node. Once we get

there, we pick another edge that we haven’t used before arbitrarily, and so

on.

Each time we enter or leave a node, we use up two of its edges (because

we are not allowed to use an edge more than once). Hence, if the node had an

even degree initially, the number of available edges at that node will remain

even. As a consequence, we won’t get stuck in a dead end. In other words, our

“just go ahead” strategy will eventually lead us back to the node where we

started.

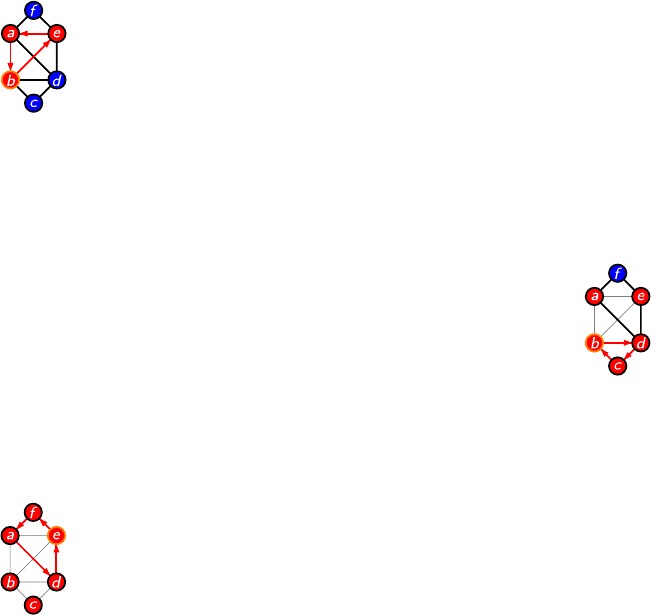
In the left ﬁgure a circuit (i.e., a route through several edges

that leads back to the origin) consisting of three edges has

emerged. The circuit passes through the vertices b, e,anda.

Yet following the above strategy (“start somewhere and keep

on going until you get back to the origin”) does not necessar-

ily yield a circuit that covers all edges. Namely, we could have

taken a “shortcut” at some node, thereby skipping a part of the

ﬁgure. If this happens, we will need to extend the circuit that we have con-

structed so far. Before we do this, we remove the edges that we have visited

already (because we are not allowed to pass through the same edges again

anyway).

For instance, in the above ﬁgure upon returning to the origin

b, we can repeat the same procedure to construct another circuit.

In the above example the second circuit is a triangle through the

nodes b, d,andc (right ﬁgure).

Linking the two circuits that we have obtained so far, we

obtain a longer circuit (b,e,a,b,d,c,b). Alas, even this circuit

does not comprise all the edges. Hence, we are in for another

extension. Of course, since all the edges that pass through the start vertex

b are already used up, we need to pick another vertex to construct the next

circuit.

Observe that removing all edges that our current circuit

(b,e,a,b,d,c,b) passes through leaves us with a ﬁgure in which

all nodes have even degrees. Hence, we can easily ﬁnd yet an-

other circuit as follows: Pick a node on the “old” circuit that

has an edge that we haven’t visited yet. Declare this node the

new starting vertex and proceed to ﬁnd another circuit by fol-

lowing the “just draw ahead” strategy. In the above example we

get the quadrangle with the corners a, d, e,andf as shown in the left ﬁg-

ure.

Thus, in addition to our “old” circuit we have got a new one that starts

and ends at some node of the old circuit. Now, the plan is to hook the new