Vilasi G. Hamiltonian Dynamics
Подождите немного. Документ загружается.



Chapter
3
Transformation
Theory
3.1
Canonical, Completely Canonical
and
Symplectic Trans-
format ions
3.1.1
Canonical transformations
The differential equations of motion have been brought into a particularly
desirable form, the
canonical
form:
However, no direct integration method of the canonical system is known. There
exist indirect methods which allow
to
highly simplify the integration problem.
One
of
them is the method
of
coordinate transformations, whose goal is to find
new coordinates, namely
(r,
x),
in which the characteristic function
%!
of the
canonical system is “more simple.” For a generic coordinate transformation,
the canonical system is not
form
invariant;
i.e., its form is not preserved.
Therefore, the interesting preliminary problem is to characterize the set
C
of
invertible differentiable transformations which preserve the canonical form of
65

66
hnsformation
Theory
equations of motion. Any transformation satisfying this requirement, will be
called a
canonical transformation.'
It
was
already clear from the Lagrangian form of dynamics that a proper
choice of coordinates
can
greatly faci~itate
the
search
for
the
solutio~
of
the
differential equations of motion.
For
instance, since a first integral of the
Lagrange equation
is
known whenever one
of
the Lagrangian coordinates is
cyclic, it is of great interest to produce cyclic coordinates
by
transforming the
original ones.
Let
be
an invertible differentiable tr~sformation from the coordinates
(~/p)
to
(x,n),
which may depend on time
t.
It was proven
by
Sophus Lie? that
A
suficient condition
for
Eq.
(3.1)
to define a canonical transformation
is
that there exist two functions
310
and
f
of
(q/p/x/~/t) such that the relation
h
h
identical@ holds. The new characteristic function
is
k;
=
(31
-
'?fo),*
where
the symbol
*
indicates that
all
coordinates
(p,q)
have been expressed
in
terms
of
(T/X).
*The theory
of
canonical transformations
is
essentially due to Jacobi whose efforts were
too much bent on the integration problem to which Hamilton was only incidentally interested.
The resulting integration theory played an important part in the modern development of
atomic physics.
tMarius Sophus Lie was born
at
Nordfjordeide (Norway) on
1842
and died in
Oslo
on
1899.
He was a professor at
Oslo
University from
1872
to
1885,
at
Lipsia University from
1866
to
1987
and again at
Oslo
University from
1898
to
1889.
It
is
difficult to illustrate,
in
a
short note,
its
enormous contribution to mathematics. He invented, in particular, the
theory of contact transformations, the theory of (finite and infinite) Lie groups, the theory
of
minimal surfaces, the theory of translation surfaces, the theory
of
surfaces with geodesical
groups,
the theory of surfaces with constant curvature. Many results
of
M.S.Lie have been
recovered, independently, by excellent modern mathematicians, after almost
100
years. We
just mention here the
Konstant-Kirillov-Souriau
symplectic structure.
*Here
identicalty
means that once the transformation
(3.1)
has been pedormed, the
relation
(3.2)
reduces to an identity.

Canonical, Completely Canonical and Symplectic hnsjonnations
67
It is a trivial exercise to verify that the transformation
is
a
canonical one; the new canonical system being
with
iC
=
a/3%!*,
but it does not satisfy the condition
(3.2).
We
can argue that the set
C
of canonical transformations is larger than the
one characterized by the Lie condition
(3.2).
It
was
later proven by Lee H~a-Chung~~ how the condition
(3.2)
can be
generalized, in order to express
a
necessary and sufficient condition
for
Eq.
(3.1)
to be
a
canonical transformation.
A
heuristic way to find a necessary and sufficient condition for a differen-
tiable invertible transformation to be canonical
is
the following.
By
using the variational principle, the Hamilton equations can be written
as
6S=O,
where
In this way, associated with the transformation
we
have the following picture:

68
‘lhnsfonation
Theoiy
$as=o
$as*
=o
Therefore, the necessary and sufficient condition
for
a
differentiable invert-
ible transformation to be canonical is that
where
S*[x/r/t]
is the transformed
of
S[q/p/t].
multiplicative constant
c,
differ by an exact differential
form
dF:
The above equivalence will be certainly true if differential
forms, up
to
a
h
\h
/
It
was
shown by Lee Hua-Chung that the condition is also necessary.
We can conclude that
A
necessary and su~c~ent condit~on for
a
di~e~e~tiab~e invert~b~e truns-
fo~ation
(3.1)
to be canon~cal
is
the existence
of
a
wnstant
c
and
of
two
functions,
3to
and
F,
of
(q/p/x/T/t),
such that the relation
phdqh
=
c
nhdXh
+
Xodt
+
df
(3.3)
h
h
ident~ca~l~
hold^.
The new charucte~stzc functzon
is
X:
=
l/c(%
-
?lo)*,
where
the
symbol
*
indicates that
all
coordinates (p,q) have been expressed
in
terns
A
simple example of canonical transformation, with
%O
=
0
and
F
=
pq,
of
(r/x).
is
given by
(3.4)
X
=
arctan(Aq/p).

Canonical,
Completely
Canonical and Symplectic lhnsformations
69
Indeed,
pdq
-
ndX
==
pdq
-
2x
1
(p2
-t
X2q2)d
(arctan
($)
)
3.1.2
A
particular class of canonical transformations is generated by an arbitrary
function
V
which depends on “one half” of original coordinates and on “one
half” of the new ones, for instance on
q’s
and
71%.
The
fmction
is
only required to satisfy the condition that the mixed hnc-
tional determinant
A
general ctase
of
canonical ~~ns~~~ut~on~
does not identically vanish
3
#
0.
It
is
easy to see that the relations
implicitly define an invertible differentiable coordinate transformation between
the
p,
q’s
and
r,
x’s.
In
fact, since
9
#
0,
by the implicit function theorem,
the second of relations
(3.5)
can
be solved in the form
qh qh(n/X/t)
and associated to the
first
one to give an explicit one-to-one transformation
between the coordinates
(p,
q)
and
(x,
x).
As
for the canonical character, it
is
enough to observe that Lie’s condition
is
satisfied:
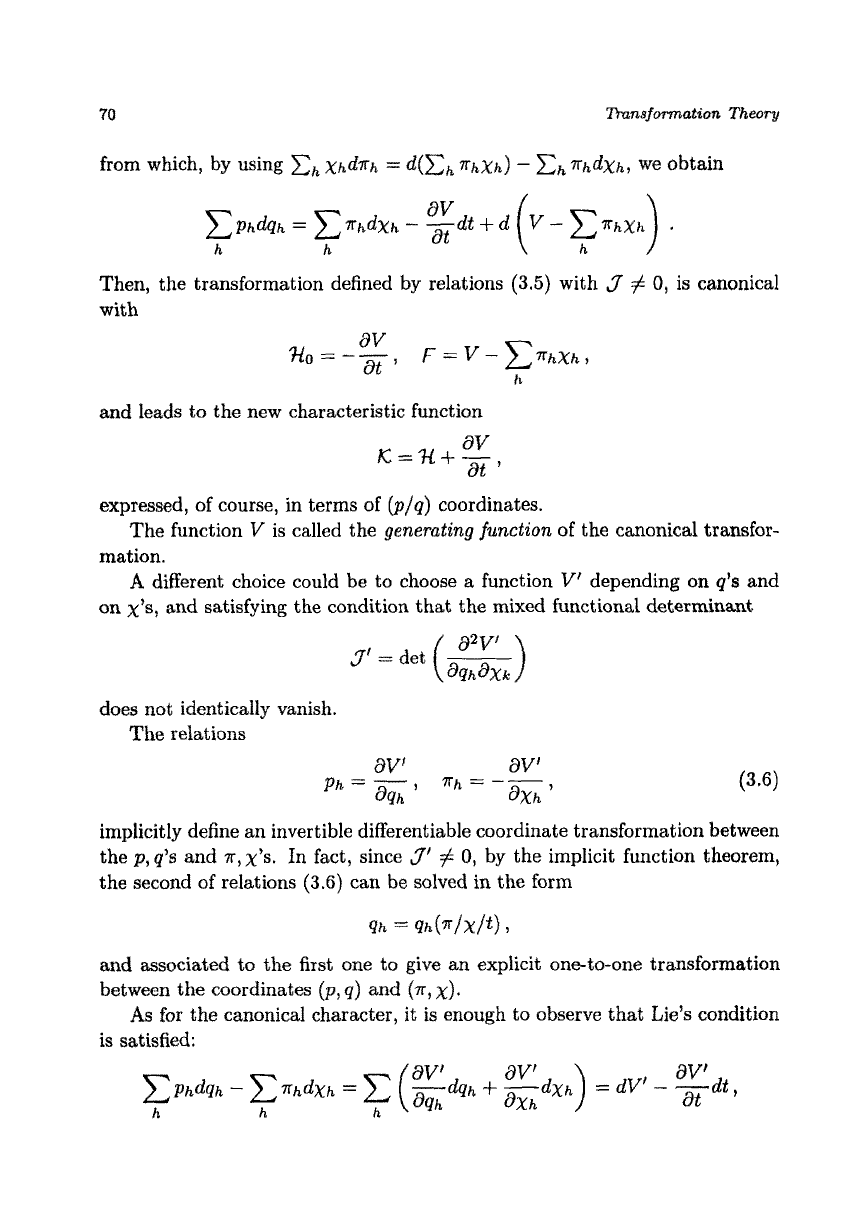
Then, the transformation defined
by
relations
(3.5)
with
3’
#
0,
is
canonical
with
and leads to the new characteristic function
aV
K=%+-,
at
expressed,
of
course, in terms of
Ip/q)
coordinates.
mation.
on
x’s,
and satisfying the condition that the mixed functional determinant
The function
V
is called the
generating
function
of the canonical transfor-
A
different choice could be to choose a function
V’
depending on
q’s
and
does not identically vanish.
The relations
(3.6)
implicitly define an invertible differentiable coordinate transformation between
the
p,
q’s
and
x,
x’s.
In fact, since
J’
#
0,
by the implicit function theorem,
the second of relations
(3.6)
can
be
solved
in
the form
qh
=
qh(~/X/~}
2
and associated
to
the first one
to
give an explicit one-to-one transformation
between the coordinates
(p,
q>
and
(T,
x).
As
for the canonical character,
it
is
enough to observe that Lie’s condition
is
satisfied:

Canonical, Completely Canonical and Symplectic 'Pransformations
71
from which we obtain
Then, the transformation defined by relations
(3.6)
with
3'
#
0,
is canonical
with
and leads to the new characteristic function
dV'
K:=x+-
at
'
expressed, of course, in terms of
(p/q)
coordinates.
transformation.
The function
V'
is
also called the
generating function
of the canonical
3.1.3
Completely canonical transformations
It has been shown that a canonical transformation
of
a given canonical sys-
tem with characteristic function
'fl
leads to
a
canonical system having
Ic
=
(l/c)(%
-
'?LO)*
as
characteristic function. When the function
K
=
(l/c)(%
-
?LO)*
reduces to
K:
=
(l/c)(%)* the transformation is called
a completely canon-
ical transformation.
Then, a necessary and sufficient condition for a canonical
transformation to be a completely canonical one is that
'tlo
=
0.
It
is
easy to see that
a
canonical transformation
which does not explicitly depend on time
t,
is a completely canonical one.
The Lie condition
(3.3)
for the transformation
(3.7)
gives
k
h

72
Runsfomation
Theory
or
equivalently,
[
(mk
f
~)
dpk
f
(@k
-b
2)
dql]
f
(..
4-
$)
dt
=
0,
where the functions
@k
and
ikk
are defined by
@k(P/Q)
=
cx
Pi-
a$Ji
apk
I
@k(P/q)=cc(oi~-Pk.
i
i
It
follows that
F
has to satisfy the following relations:
aF
No
+
at
=
0.
df
Moreover,
as
@k
and
ikk
do not explicitly depend on time
t,
we
&so
have
or
equivalently,
which implies that
dF/&
does not depend
on
the
p’s
and the
q’s
but only
on
t.
From
BF
dt
-
=
f(t>
,
it follows that
and
Therefore, Lie’s condition
(3.3)
becomes
so
that the new characteristic function is simply
Ic
=
(l/c)(N)*.

Canonicul, Completely Canonical and Symplectic Thnsformations
73
3.1.4
Sgmplectic transformatione
A
canonical transformation, which leads to a new characteristic function
K
of the form
K
=
(%)*,
is called a
symplectic transformation.
Therefore, a
symplectic transformation is a completely canonical transformation with
c
=
1.
The following picture summarizes all the cases well:
K
=
-(N
-
No)*
1
(canonical),
C
K:
=
-(N)*
1
(completely canonical)
,
(3.8)
C
K
=
(N)*
(symplectic)
.
The transformation
(3.4) of
the previous example is a symplectic transforma-
tion with
a
generating function given by
3.1.5
Area presenting transformations
An invertible differentiable map from
R2
to itself,
will transform
a
given Lebesgue measurable region
S
C
R2
in a measurable
region
C
2
R2,
The map will be said an
area-preserving transformation,
or
simply, an
equiv-
alent transformation,
if the measures of
S
and
C
coincide:
mz(S)
=
m2(C).
Theorem
13
A
necessary and suficient condition for an invertible
transformation on
R2,
to be symplectic
is
to
be
an area preserving transformation.
