Вестник Северо-Кавказского государственного технического университета 2011 №1 (26)
Подождите немного. Документ загружается.


Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
«Северо-Кавказский государственный технический университет»
ВЕСТНИК
Северо-Кавказского государственного
технического университета
№ 1 (26) Журнал основан в 1997 г. 2011
Выходит 4 раза в год
Главный редактор
Синельников Б. М. – доктор хим. наук, профессор,
действительный член Академии технических наук Российской Федерации.
Редакционная коллегия
Слюсарев Г. В. – доктор техн. наук, профессор, проректор по науке, информатизации и инновационной деятельности
(председатель); Бавижев М. Д. – доктор физ.-мат. наук, профессор; Бережной В. И. – доктор экон. наук, профессор;
Валюхов Д. П. – доктор хим. наук, профессор; Ветров Ю. П. – доктор пед. наук, профессор; Воробьев В
. А. – доктор
техн. наук, профессор; Галай Б. Ф. – доктор геол.-мин. наук, профессор, академик РАЕН; Горлов С. М. – доктор экон.
наук, профессор; Евдокимов И. А. – доктор техн. наук, профессор; Игропуло И. Ф. – доктор пед. наук, профессор;
Клушина Н. П. – доктор пед. наук, профессор; Кононов Ю. Г. – доктор
техн. наук, доцент; Куницына Н. Н. – доктор
экон. наук, профессор; Мартенс В. Я. – доктор техн. наук, доцент; Новожилов А. А. – доктор хим. наук, профессор;
Петренко В. И. – доктор геол.-мин. наук, профессор, академик РАЕН; Парахина В. Н. – доктор экон. наук, профессор;
Серов А. В.
– доктор техн. наук, доцент; Стоянов Н. И. – доктор техн. наук, доцент; Тагиров К. М. – доктор техн.
наук, профессор; Труфанов М. Е. – доктор юр. наук, доцент; Ушвицкий Л. И. – доктор экон. наук, профессор;
Храмцов А. Г. – доктор техн. наук, профессор, академик РАСХН; Шаповалов В. К. – доктор пед. наук
, профессор;
Шевчук С. С. – доктор юр. наук, профессор.
Учредитель
Государственное образовательное учреждение
высшего профессионального образования
«Северо-Кавказский государственный технический университет»
Научно-исследовательский журнал зарегистрирован в Министерстве Российской Федерации по делам печати,
телерадиовещания и средств массовых коммуникаций. Свидетельство о регистрации средства массовой информации
ПИ № 77-17070 от 26 ноября 2003 г.
Подписной индекс 20449 в федеральном каталоге периодических изданий ОАО Агентства «Роспечать».
Журнал включен в Перечень ведущих рецензируемых научных журналов и изданий, в которых
должны быть
опубликованы основные научные результаты диссертаций на соискание ученых степеней доктора и кандидата наук.
Адрес:
355028, г. Ставрополь, пр. Кулакова, 2
Телефон:
(8652) 94-42-01, (8652) 56-26-70
E-mail: rio@stv.runnet.ru
© Коллектив авторов, 2011
© ГОУ ВПО «Северо-Кавказский
государственный технический
университет», 2011

Вестник Северо-Кавказского государственного технического университета. 2011. № 1 (26)
3
СОДЕРЖАНИЕ
ФИЗИКА, ХИМИЯ
Голубин М. А., Дерябин М. И., Добровольская И. А., Шаповалова А. М., Беляева Е. Н.
Кинетика аннигиляционной замедленной флуоресценции изолированных пар и её
математическая модель……………………………………………………………………………..
6
Ратнер И. М. Двумерная модель изинга с тремя возможными состояниями узлов…………... 10
Сидоров К. И., Лисицын С. В., Зубрилов В. Г., Пигулев Р. В., Валюхов Д. П. Методика
исследования гидрогенизированного карбида кремния масс-спектрометрией вторичных
нейтральных частиц………………………………………………………………………………...
16
Шевченко Е. Ф., Мартенс В. Я. Ионная очистка подложек микроплат в установке
вакуумного напыления как альтернатива химической очистке…………………………………
19
ИНФОРМАЦИОННО-ТЕЛЕКОММУНИКАЦИОННЫЕ СИСТЕМЫ
Чипига А. Ф., Шевченко В. А., Сенокосова А. В., Дагаев Э. Х. Оценка влияния
поглощающих свойств ионосферы ее неоднородностей на среднюю энергию сигнала на
входе приемника спутниковой связи………………………………………………………………
24
Чипига А. Ф., Шевченко В. А., Сенокосова А. В., Дагаев Э. Х. Математическая
модель трансионосферного канала с учетом поглощения и многолучевости
принимаемого сигнала……………………………………………………………………………
32
УПРАВЛЕНИЕ, ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА
И ИНФОРМАТИКА
Маликов А. В., Сугаков М. И., Турьев А. А., Дроздова В. И. Проектирование баз данных
с использованием темпоральных деревьев……………………………………………………….
41
Подопригора Н. Б., Федоренко И. В. Особенности задач моделирования и оптимизации
многоканальных информационных систем методами теории игр……………………………...
46
Узденов А. А., Кочкаров Р. А. Алгоритм поиска центра предфрактального графа,
смежность старых ребер которого сохраняется………………………………………………….
50
ЭНЕРГЕТИКА
Демин М. С. Разработка и моделирование помехоустойчивого датчика тока с малыми
потерями для импульсного синхронного понижающего преобразователя напряжения……….
54
Седова И. Ю., Юдина О. И. Моделирование добавочных потерь в системе «двигатель
постоянного тока – силовой полупроводниковый преобразователь»……………………………
57
МАШИНОСТРОЕНИЕ И ТРАНСПОРТ
Сидоренко С. А., Лозовая Е. Б. Разработка импульсных вращателей для обработки
материалов повышенной прочности……………………………………………………………….
63
Сидоренко С. А., Мелихова М. С. Координатный метод определения профиля поверхности
при обработке тел вращения методом торцового фрезерования…………………………………
66
НАУКИ О ЗЕМЛЕ
Бурым Ю. В. Анализ временной структуры предгорных и среднегорных ландшафтов
Ставропольского края с использованием ГИС-технологий………………………………………
70
Витько Е. В., Кирвякова А. В. Современное состояние мирового и российского лесного фонда 75
Вобликов Б. Г., Стерленко З. В., Туманова Е. Ю., Филипович П. А. О метаморфизме
нижней части осадочного
чехла палеозойского возраста в разрезах скважин
Восточного Ставрополья……………………………………………………………………………
80
Гайрабеков И. Г. Определения деформационной поверхности, совпадающей с перекрытием
цокольного этажа……………………………………………………………………………………
84
Гайрабеков И. Г., Пимшин Ю. И. Особенности учета сверхнормативных неравномерных
кренов конструкций при подъеме и выравнивании многоэтажных зданий…………………………….
88
Петренко В. И., Чурсинов С. К. Масштабы
нарушения динамического и флюидального
равновесия в земной коре при разработке газовых и газоконденсатных месторождений
и их следствия……………………………………………………………………………………….
92
Вестник Северо-Кавказского государственного технического университета. 2011. № 1 (26)
4
Смольникова В. В. Выживание дождевых червей в условиях нефтяного загрязнения……… 95
Терехов В. И., Таранков В. И. Влияние экспозиции склона на углеродный и кислородный
баланс в байрачных дубравах Курской области…………………...................................................
100
Чурсинов С. К., Басов А. А., Тагиров О. О. Опыт газопескоструйной перфорации газовой
скважины с АНПД на депрессии…………………………………………………………………...
105
СТРОИТЕЛЬСТВО
Гутенева С. В., Гаврилова А. И. Причины аварий каменных зданий и элементов…………... 111
Стоян И. А., Пчелинцев С. Г., Рожков П. В., Чурин П. С. Выбор экономичной ширины
отводящего канала берегового водосброса………………………………………………………..
114
Скориков С. В., Лозикова Ю. Г. Изучение влияния добавок цемента на свойства
битумоминеральных композиций на эмульгированных битумах………………………………..
117
ИНЖЕНЕРНО-АГРОПРОМЫШЛЕННЫЕ СПЕЦИАЛЬНОСТИ
Грицаева М. В., Серов А. В., Храмцов А. Г. Перспективные направления использования
солей молочной кислоты (лактатов)……………………………………………………………….
120
Борисенко А. А., Борисенко Л. А., Моргунова А. В., Митякина Ю. В., Брацихин А. А.
Влияние активированной воды на функционально-технологические свойства белкового
препарата «Кат-гель 95»………………………………………………………………………….....
124
Смольникова В. В., Емельянов С. А. Применение молочной сыворотки при
компостировании растительного сырья……………………………………………………………
127
Остриков А. Н., Синюков Д. А. Исследование кинетики процесса вакуум-выпаривания
поликомпонентных фруктовых пюре………………………………………………………………
131
ФИЛОСОФИЯ И СОЦИОЛОГИЯ
Анисимова О. П. Теоретические подходы к последипломной подготовке специалистов
социальной сферы к первичной профилактике аддиктивного поведения подростков…………
136
Нижников С. А. Проблемность понятия красоты в творчестве Ф. М. Достоевского…………. 140
Пьянов А. И. Семья как объект социального познания (к методологии социологического
исследования)………………………………………………………………………………………..
146
ПЕДАГОГИКА И ПСИХОЛОГИЯ
Горлова Е. Б. Основные подходы к организации психосоциальной помощи гражданам,
пострадавшим в результате террористического акта……………………………………………..
151
Гришанина О. А., Махиня Л. Н. Основные виды учебной деятельности в сетевом
обучении общетехническим дисциплинам в СевКавГТУ………………………………………...
154
Ковалева О. И., Черепкова Н. В. Методологические и антрополого-гносеологические
основы средового развития личности подростка………………………………………………….
159
Коныгина М. Н. Историко-культурные ориентиры построения профессиограммы
специалиста социальной работы……………………………………………………………………
164
Найденова Г. И. Формирование мотивации самообразования в условиях проектной
деятельности студентов……………………………………………………………………………..
168
Савелло Е. В. К проблеме билингвальной подготовки будущих инженеров………………….. 173
Харченко Л. Н., Панова И. Е. Обоснование инновационного подхода к оценке
эффективности образовательного процесса……………………………………………………….
177
ПРАВО
Горбаруков В. А. О некоторых способах совершения преступлений против собственности с
использованием ЭВМ……………………………………………………………………………….
182
Динаев Р. Р. Особенности проведения осмотра места происшествия при расследовании
грабежей и разбойных нападений, совершенных в отношении малолетних……………………
184
Кормилина Е. В. Специфические обстоятельства, подлежащие установлению, и
особенности первоначального этапа расследования преступлений, связанных
с неисполнением обязанностей по воспитанию несовершеннолетних…………………………..
186
Лисин С. Н. Типичные ситуации первоначального этапа расследования преступлений,
связанных с незаконной добычей водных животных, растений и незаконной охотой…………
188

Вестник Северо-Кавказского государственного технического университета. 2011. № 1 (26)
5
Найманов Т. Ю. Особенности проведения проверки показаний на месте при расследовании
преступлений, связанных с криминальной деятельностью организованных преступных
групп и преступных сообществ в сфере грузоперевозок на автодорогах……………………….
191
Черников С. В. Нравственно-этические основы деятельности следователя…………………... 194
Чмелев А. А. Организация органов предварительного следствия в годы становления
Советского государства……………………………………………………………………………..
196
ЭКОНОМИКА
Бережной В. И., Зенченко С. В., Родченко А. М. конкурентные преимущества регионов
Северо-Кавказского федерального округа: возможности и угрозы ………………………...
201
Боташев А. Ю. Состояние и экономическая оценка деятельности агропромышленного
комплекса Карачаево-Черкесской республики………………………………………...………….
205
Бражников А. С. Методы сводной оценки качества кредитного портфеля коммерческого
банка………………………………………………………………………………………………….
210
Вержбицкая И. В. Становление судебно-бухгалтерской экспертизы. Ее предмет и объекты.. 215
Гладилин А. В., Боташев А. Ю. Методические подходы в организации информационно-
консультационного обеспечения регионального АПК……………………………………………
220
Говядовская О. В. Эволюционная основа сущности и функций стратегического управления
развитием сельскохозяйственного сектора………………………………………………………..
224
Грендач Е. А.
Совершенствование системы
VIP-обслуживания в коммерческом банке….…
228
Джавадова О. М. Проблемы развития туристического комплекса Ставропольского края…… 232
Кипа Е. Г. Применение аналитических процедур при экспертном исследовании
обязательств………………………………………………………………………………………….
236
Климова О. А. Рыночные риски коммерческих банков: МСФО и Базель II…………………... 240
Ковязина Е. В. Бюджетная самостоятельность как основа функционирования
муниципального образования………………………………………………………………………
242
Колесников А. А. Оптимизация организационной структуры службы финансового
мониторинга………………………………………………………………………………………….
247
Лазарева Н. В., Фурсов В. А. Формирование системы мониторинга предпринимательской
среды регионального рынка транспортных услуг…………………………………………………
251
Лобанова С. В. Реструктуризация как метод повышения инвестиционной
привлекательности сельхозпредприятий региона…………………………………………………
256
Мирюшкина Ю. В. Факторы и способы обеспечения развития современной инновационной
экономики……………………………………………………………………………………………
259
Мурадова Ю. А. Проблемы законодательного регулирования государственно-частных
партнерств……………………………………………………………………………………………
262
Сорокин А. А. К методике анализа результатов обследования пассажиропотоков…………… 267
Цыбульский А. И. Практическая реализация теории рефлексивного управления при оценке
конкурентных позиций субъектов транспортной деятельности………………………………….
272
Информация об авторах................................................................................................................... 278
К сведению авторов. Порядок рецензирования статей в журнале…………………….......... 281
Условия и требования к опубликованию в журнале…………………………………………. 282

Вестник Северо-Кавказского государственного технического университета. 2011. № 1 (26)
6
ФИЗИКА, ХИМИЯ
УДК 535.373.2
КИНЕТИКА АННИГИЛЯЦИОННОЙ ЗАМЕДЛЕННОЙ ФЛУОРЕСЦЕНЦИИ
ИЗОЛИРОВАННЫХ ПАР И ЕЁ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Голубин М. А., Дерябин
М. И.
*
, Добровольская И. А.
**
, Шаповалова А. М.
*
, Беляева Е. Н.
*
Ставропольский государственный университет,
**
ГОУ ВПО «Невинномысский государственный гуманитарно-технический институт»
Исследована кинетика затухания аннигиляционной замедленной флуоресценции (АЗФ) изолированных пар в
н.-парафиновых матрицах при 77 К. Показано, что в отсутствие статистического разброса констант скоростей
триплет-триплетной аннигиляции (ТТА), затухание АЗФ изолированных пар происходит по экспоненциальному закону.
The kinetics of delayed annihilation fluorescence (SAF) fading of isolated pairs in n.-paraffin matrices at 77 K has been
studied in this paper. It was shown that at the absence of rates constants statistic dispersion of triplet-triplet annihilation (TTA),
the SAF annihilation of isolated pairs is taken place according to exponential law.
Ключевые слова: триплет-триплетная аннигиляция (ТТА), замедленная флуоресценция (ЗФ), 1,2-бензпирен
(1,2-БП), коронен.
Key words: triplet-triplet annihilation (TTA), delayed fluorescence (DF), 1,2-banzpyrene, coronene.
Введение
В экспериментальных исследованиях природы излучающих центров и механизмов свечения
органолюминофоров важное место, наряду со спектральными, занимают кинетические методы
[1, 2], то есть изучение процессов разгорания и затухания люминесценции. Определённые
из кинетических экспериментов параметры являются характеристиками как самих центров [1], так
и их взаимодействия между собой и с матрицей [2]. По этой причине для изучения как
межмолекулярных взаимодействий [2], так и структурных особенностей окружения [3] широко
используется замедленная флуоресценция органических молекул, возникающая при аннигиляции
триплетных возбуждений. Возникновение возбуждённого синглетного состояния при аннигиляции
двух триплетных возбуждений требует эффективного сближения последних, чтобы
межмолекулярные обменные интегралы были достаточно велики [4]. Сближение триплетно-
возбуждённых молекул в жидких растворах органических соединений обусловлено их диффузией.
В результате этого АЗФ в жидких растворах органических соединений является результатом ТТА,
контролируемой диффузией [5].
В неупорядоченных твёрдых средах (активированных стёклах, полимерных матрицах и др.),
даже в отсутствие диффузии молекул люминофора, сближение триплетных возбуждений
с последующей аннигиляцией может происходить в результате их миграции по триплетным
уровням активатора [3, 6]. В данном случае
АЗФ является результатом ТТА контролируемой
миграцией возбуждений по триплетным уровням примесных центров. В обоих указанных выше
случаях между актами возникновения и аннигиляцией двух триплетных возбуждений существует
промежуточный процесс их эффективного сближения.
В поликристаллических н.-парафиновых растворах (матрицы Шпольского) и при малых
концентрациях примесных молекул в стеклообразных средах ТТА может происходить
в
изолированных (невзаимодействующих) парах. Здесь отсутствует промежуточный процесс
их сближения. Следствием отсутствия процесса сближения является то, что в изолированных парах
не все триплетные возбуждения могут участвовать в процессе ТТА. При наличии же процесса
сближения все триплетные возбуждения участвуют в процессе ТТА. Несмотря на столь очевидное
различие, считается, что в обоих случаях аннигиляция триплетных возбуждений [3, 6, 7] протекает
согласно формальному кинетическому уравнению:
2
1
T
T ан T
dn
kn k n
dt
−=+
, (1)
где
T
n – концентрация молекул в триплетном состоянии;
1
k – мономолекулярная константа
скорости дезактивации триплетно-возбуждённых молекул, связанная с временем жизни триплетного
состояния соотношением
1
1T
k
τ
−
= ;
ан
k – бимолекулярная константа скорости аннигиляции.

Вестник Северо-Кавказского государственного технического университета. 2011. № 1 (26)
7
Считается, что в однородных средах
ан
k не зависит от времени [6], а в дисперсной среде
скоростной коэффициент ТТА становится зависящим от времени [8]. Предполагается,
что интенсивность АЗФ прямо пропорциональна квадрату концентрации триплетных возбуждений
АЗФ
I
~
2
T
n . (2)
Согласно известному решению (1), с учётом (2) затухание АЗФ в однородных средах должно
описываться уравнением:
1
2
1
0
() [(1 ) 1]
kt
ан
k
It I e
k
−
=+ −, (3)
где
0
I
– интенсивность АЗФ в начальный момент времени. В случае дисперсной среды кинетика
затухания АЗФ имеет более сложную временную зависимость.
Таким образом, согласно существующим моделям затухание АЗФ в общем случае должно
иметь неэкспоненциальный характер. Только при
1ан
kk
<
< , когда дезактивацией триплетных
возбуждений в результате аннигиляции можно пренебречь, затухание АЗФ как в однородной, так
и в дисперсной среде, становится экспоненциальным с характерным временем
1
12k
τ
= .
С помощью выражения (3) не удаётся описать кинетику затухания АЗФ изолированных пар
на всех её стадиях [5, 7] при
1ан
kk≥ . На наш взгляд, это связано с тем, что уравнение (1)
и соотношение (2) справедливы только при наличии промежуточного процесса сближения
возбуждений между актами возникновения триплетных возбуждений и их аннигиляцией.
Для изолированных пар, где процесс сближения возбуждений отсутствует, уравнение (1)
и соотношение (2) применять нельзя.
Критический анализ существующей модели
Уравнение (1) и соотношение (2) основываются на двух предположениях. Во-первых,
считается, что квант излучения АЗФ возникает за счёт объединения двух триплетных возбуждений.
Во-вторых, считается, что все триплетные возбуждения могут участвовать в процессе ТТА. Однако
эти два условия выполняются одновременно только для АЗФ контролируемой диффузией (жидкие
растворы) и для АЗФ контролируемой миграцией
триплетных возбуждений (твёрдые растворы).
В случае изолированных пар второе условие не выполняется, на что не обращается внимание при
использовании выражения (2) в этих условиях. Действительно, для осуществления триплет-
триплетной аннигиляции необходимо, чтобы обе молекулы в изолированной паре находились
в триплетном состоянии. В дальнейшем такую пару будем называть триплетно-возбуждённой.
Триплетно-возбуждённая
пара может исчезнуть как в результате триплет-триплетной аннигиляции,
так и в результате внутримолекулярной дезактивации триплетного возбуждения одной из молекулы.
В последнем случае, после внутримолекулярной дезактивации возбуждения одной молекулы,
вторая остаётся в триплетном состоянии и в отсутствие возбуждения не может принимать участие
в процессе излучения замедленной флуоресценции. Однако выражение (2), как и
(1), включают
в себя эти молекулы. Именно поэтому уравнение (3), полученное на основании решения (1)
с учётом (2), не может адекватно описывать кинетику затухания аннигиляционной замедленной
флуоресценции изолированных пар в общем случае.
Новая модель кинетики ТТА и АЗФ изолированных пар
Поскольку для излучения АЗФ необходимо, чтобы обе молекулы в паре находились
в возбуждённом триплетном стоянии, то её интенсивность должна быть прямопропорциональна
концентрации триплетно-возбуждённых пар N, т. е. удовлетворять соотношению
АЗФ
I
~N
T
, (4)
а не соотношению (2). Впервые на это было обращено внимание в работе [7].
Если константы скорости
ан
k
1
k одинаковы для всех триплетно-возбуждённых пар, то их
убыль после прекращения возбуждения протекает согласно кинетическому уравнению:
1
2
T
T ан T
dN
kN k N
dt
−= + . (5)
Здесь
1
2k – константа скорости распада триплетного возбуждённых пар в результате
перехода одной из молекул в основное состояние. Решение (5) хорошо известно и имеет вид:
0
1
( ) exp[ (2 ) ]
TT ан
Nt N k k t=−+. (6)

Вестник Северо-Кавказского государственного технического университета. 2011. № 1 (26)
8
Таким образом, в отсутствие статистического разброса констант скоростей
ан
k
ан
k
ан
k
и
1
k ,
убыль триплетно-возбуждённых пар происходит по экспоненциальному закону (6) с характерным
временем
1
1
(2 )
Зан
kk
τ
−
=+ . (7)
Следовательно, с учётом соотношения (4) затухание АЗФ изолированных пар происходит по
экспоненциальному закону:
0
3
( ) exp( )
АЗФ АЗФ
ItI t
τ
=−, (8)
где
0
АЗФ
I
– интенсивность АЗФ в начальный момент времени.
В предельном случае при
1ан
kk<< затухание АЗФ происходит с характерным временем
1
12
З
k
τ
= , что совпадает с предельным случаем для выражения (6).
Очевидно, что при наличии случайного распределения пар по константам скоростей
31
2
ан
kkk=+ кинетика затухания АЗФ изолированных пар представляет собой сумму бесчисленного
числа экспонент. В этом случае, как было показано в [7], затухание люминесценции протекает
согласно формальному уравнению:
0
12
21
( ) [exp( ) exp( )]
()
I
I
ttt
t
αα
αα
=−−−
−
. (9)
Здесь
2
α
соответствует наибольшему значению
3
k , а
1
α
– наименьшему.
Наличие статистического распределения пар по межмолекулярному расстоянию в них
и взаимной ориентации молекул приводит к статистическому разбросу
ан
k , вследствие чего
характер кинетики АЗФ становится многоэкспоненциальным и, как показано в [7],
удовлетворительно описывается уравнением (9).
В н.-парафиновых матрицах (системах Шпольского) часть молекул может внедряться
в кристаллическую решётку растворителя по принципу замещения, а часть вытесняться в различного
рода деффекты. Можно ожидать, что для аннигилирующих пар, внедрённых в решётку растворителя,
функция распределения
по межмолекулярному расстоянию близка к дельта-фукции. Следовательно,
затухание излучения АЗФ данных пар должно быть близко к зависимости (8), что позволяет
с использованием выражения (7) определять для них значение
ан
k .
Экспериментальные методы
1,2-БП марки «ХЧ» не подвергался дополнительной очистке. Растворитель додекан марки
«ХЧ» дополнительно очищался методом фракционной перегонки. Исходная концентрация молекул
1,2-БП в жидком додекане при комнатной температуре была 10
-4
моль/л. Измерения производились
при 77 К. В качестве источника фотовозбуждения использовалась ксеноновая лампа ДКСШ-1000
с фильтром, пропускающим излучение с
340 нм
λ
> . Задержка между прекращением возбуждения
и началом регистрации составляла 0,01 с и осуществлялась с помощью электромеханических
затворов. Интенсивность АЗФ измерялась на
409
λ
=
нм.
Коронен также использовался марки «ХЧ» и не подвергался дополнительной очистке. В этом
случае в качестве растворителя использовался н.-октан марки «ХЧ», который дополнительно
очищался методом фракционной перегонки.
Результаты эксперимента и их обсуждения
Первая серия экспериментов проводилась по изучению кинетики затухания АЗФ 1,2-БП
в додекане при Т = 77 К. Временной интервал затухания АЗФ лежал в диапазоне 0 – 0,6 с. На рис. 1
представлена экспериментальная кривая затухания АЗФ 1,2-БП в додекане при 77 К. Анализ
показал, что 80 % интенсивности АЗФ затухает по экспоненте (сплошная линия) с характерным
временем 0, 22
З
τ
= с.
Такому значению соответствует константа скорости убыли триплетно- возбуждённых пар
3
4,54k = с
-4
. Учитывая, что
1
0,51k = с
-1
, для константы скорости
ан
k триплетных молекул 1,2-БП
ответственных за данную интенсивность АЗФ, имеем 2, 02
ан
k
=
с
-1
. Хорошее совпадение
экспериментальных значений с экспоненциальной зависимостью при 0, 22
З
τ
=
с позволяет судить
о возможности применения выражения (8), полученного на основании решения модели (5) с учётом
(4) и (6), для описания кинетики АЗФ. Отклонение экспериментальной точки, соответствующей
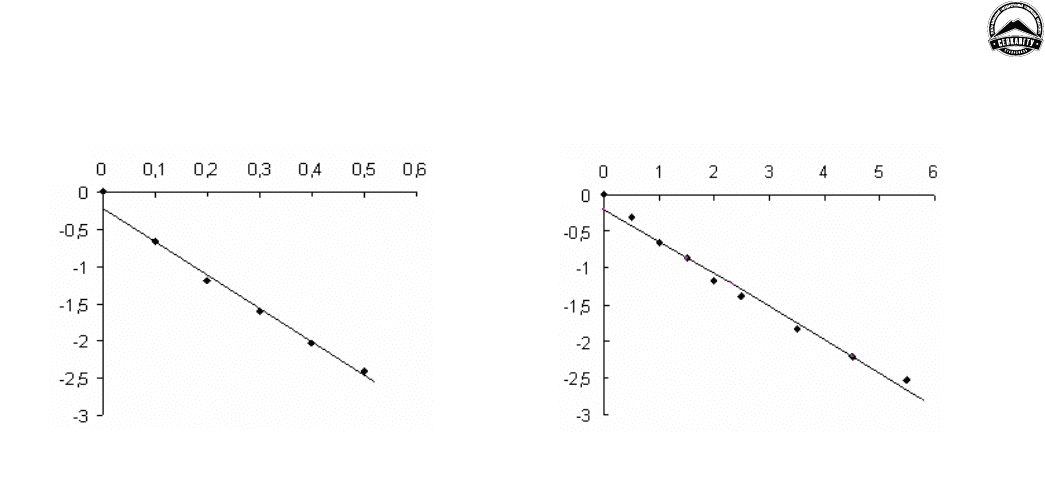
Вестник Северо-Кавказского государственного технического университета. 2011. № 1 (26)
9
начальному моменту времени, от экспоненты может быть обусловлено как сложностью
определения начальной интенсивности, так и наличием пар с другими значениями
ан
k .
Следующая серия экспериментов проводилась по изучению кинетики затухания АЗФ коронена в
н.-октане при 77 К. Временной интервал затухания АЗФ коронена лежал в диапазоне 0 – 6 с. На рис. 2
представлена экспериментальная (точки) кривая затухания АЗФ коронена в н.-октане при 77 К. Как и в
случае 1,2-бензпирена около 80 % интенсивности АЗФ коронена затухает по экспоненте (сплошная
линия). При этом время затухания равно 2, 3
З
τ
=
с. Этому значению
З
τ
соответствует константа
скорости убыли триплетно-возбужденных пар
3
0,435k
=
с
-1
. Для коронена в н.-октане
1
0,120k
=
с
-1
. С
учётом этого определённое нами 0,158
ан
k = с
-1
, что на порядок меньше, чем для 1,2-БП. На наш взгляд,
такое различие в значениях
ан
k для 1,2-БП и коронена может быть связано как с особенностями
образования аннигилирующих пар, участвующих в Т-Т аннигиляции, в матрицах Шпольского, так и
со структурой энергетических уровней молекул. Этот вопрос требует более детального изучения
в дальнейшем.
Заключение
Интенсивность АЗФ изолированных пар прямопропорциональна числу пар, в которых
обе молекулы находятся в триплетном состоянии и могут участвовать в Т-Т аннигиляции.
Моделью, основанной на пропорциональности интенсивности АЗФ квадрату концентрации
молекул в триплетном стоянии, можно пользоваться только в том случае, если между актом
возникновения триплетных возбуждений и аннигиляцией есть процесс их
сближения.
В отсутствие статистического распределения молекул по константам скоростей аннигиляции
их триплетных возбуждений затухание АЗФ изолированных пар происходит по экспоненциальному
закону. Характерное время затухания АЗФ изолированных пар позволяет определять константу
скорости аннигиляции их триплетных возбуждений.
Литература
1. Лёвшин, Л. В. Люминесценция и её измерения. Молекулярная люминесценция / Л. В. Лёвшин,
А. М. Салецкий. – М. : МГУ, 1989. – 272 с.
2. Паркер, С. Фотолюминесценция растворов / С. Паркер. – М. : Мир, 1972. – 511 с.
3. Багнич, С. А. Кинетика аннигиляции триплетных возбуждений в органических стёклах / С. А. Багнич,
А. В. Конаш // Оптика и спектроскопия. 2002. Т
. 92. № 4. С. 356 – 363.
4. Безызлучательный перенос энергии электронного возбуждения / В. Л. Ермолаев, Е. Н. Бодунов,
Е. Б. Свешников, Т. И. Шахвердов. – Ленинград : Наука, 1977. – 311 с.
5. Сапунов, В. В. О кинетике триплет-триплетной аннигиляции в жидких растворах / В. В. Сапунов // Оптика
и спектроскопия. 1995. Т. 79. № 4. С. 606 – 612.
6. Брюханов, В. В. Влияние температуры
на скорость триплет-триплетной аннигиляции 1,2-бензантрацена
в полимерной матрице / В. В. Брюханов, И. Г. Самусев, С. Г. Карстина // Журнал прикладной спектроскопии. 2004.
Т. 71. № 1. С. 49 – 53.
7. Куликова, О. И. Кинетика замедленной флуоресценции органических молекул в н.-парафиновых матрицах
и её математическая модель / О. И. Куликова, Т. В. Желудкова, В. В. Солодунов // Известия
высших учебных заведений.
Физика. 2007. № 12. С. 3 – 8.
8. Harmon, L. A. Triplet excitation transport kinetics in vapor-deposited naphthalene / L. A. Harmon, R. Kopelman //
J. Phys. Chem. 1990. Vol. 94. № 9. P. 3454 – 3461.
lnI/I
0
lnI/I
0
t, с
t, с
Рисунок 1– Экспериментальная кривая
затухания АЗФ 1, 2-БП в додекане при 77 К
Рисунок 2 – Экспериментальная (точки) кривая
затухания АЗФ коронена в н.-октане при 77 К

Вестник Северо-Кавказского государственного технического университета. 2011. № 1 (26)
10
References
1. Levshin, L. V. Luminescence and its measure. Molecular luminescence / L. V. Levshin, A. M. Saletskiy. – M. :
MGU, 1989. – 272 p.
2. Parker, C. Photoluminescence of solutions / C. Parker. – M. : Mir, 1972. – 511 p.
3. Bagnich, V. V. Kinetics of triplet excitation annihilation in a organic glasses / V. V. Bagnich, A. V. Konash // Optic
and spectroscopy. 2002. Vol. 92. № 4. P. 556 – 563.
4. Nonradiative transfer of electronic excitation energy / V. L. Ermolaev, E. N. Bodunov, E. B. Sveshnikova,
T. I. Shakhverdov. – Leningrad : Nauka, 1977. – 311 p.
5. Sapunov, V. V. On triplet-triplet annihilation kinetics in liquid solutions / V. V. Sapunov // Optic and spectroscopy.
1995. Vol. 79. № 4. P. 606 – 612.
6. Bryukhanov, V. V. Temperature effect on triplet-triplet annihilation rate of 1, 2-benzantracene in polymeric matrix /
V. V. Bryukhanov, I. G. Samusev, S. G. Karstina // Journal of Applied Spectroscopy. 2004. Vol. 71. № 1. P. 49 – 53.
7. Kulikova, O. I. Kinetics organic molecules delayed fluorescence in n-paraffin matrices and its mathematical model /
O. I. Kulikova, T. V. Zheludkova, V. V. Solodunov // News of HEI. Phusics. 2007. № 12. P. 3 – 8.
8. Harmon, L. A. Triplet excitation transport kinetics in vapor-deposited naphthalene / L. A. Harmon, R. Kopelman //
J. Phys. Chem. 1990. Vol. 94. № 9. P. 3454 – 3461.
УДК 537.612:519.6
ДВУМЕРНАЯ МОДЕЛЬ ИЗИНГА
С ТРЕМЯ ВОЗМОЖНЫМИ СОСТОЯНИЯМИ УЗЛОВ
Ратнер И. М.
НОУ «Ставропольский институт управления»
Разработан алгоритм и программа на языке Паскаль для вычисления элементов и собственных значений
трансфер-матрицы решетки Изинга с тремя возможными состояниями узлов. Приводятся результаты расчетов
собственных значений решетки без учета и с учетом внешнего магнитного поля. Результаты могут служить для
проверки моделей диагонализации трансфер-матрицы решетки подобного типа.
The algorithm and program on Pascal language to calculate elements and proper values of Easing transfer-matrix
lattice with three possible cross-points conditions have been developed. The results of lattice proper values calculations are
given without taking and with taking into consideration the external magnetic field. The results can be used to check models of
transfer-matrix lattice diagonalization of such type.
Ключевые слова: алгоритм на языке Паскаля, двумерная модель Изинга, трансфер-матрицы решетки.
Key words: algorithm on Pascal language, Easing two-dimensional model, transfer-matrix lattices.
Двумерная модель Изинга без магнитного поля была точно решена в работах Онсагера –
Кауфман [1, 2]. Предполагалось, что каждый узел решетки имеет два возможных состояния,
нумеруемых как +1 и –1. Это соответствует утверждению, что источником ферромагнетизма
является взаимодействие спинов атомов.
Представляет значительный интерес исследование возможности фазового перехода
в системе, узлы которой обладают тремя возможными состояниями. Это
может быть либо система
спаренных электронов, либо система взаимодействующих орбитальных моментов атомов.
В настоящей работе рассматривается двумерная решетка, узлы которой имеют три
возможных состояния
s, нумеруемых как s={+1, 0, –1}. Параметры взаимодействия по горизонтали
J
1
и по вертикали J
2
считаем различными. Для вычисления статистической суммы модели найдем
элементы матрицы взаимодействия (трансфер-матрицы), которую представим в симметричной
форме [3]:
)exp()
2
(exp)
2
exp(,...,,...,
!
2
!
1
!
1
1
1
!
!!
11 kk
kkkk
n
k
kk
nn
ss
ssssss
ssPss
θθβ
++
=
++
=
∏
, (1)
где
T
B
=
β
,
T
J
1
1
=
θ
,
2
2
J
T
θ
= , 2)
и
T абсолютная температура в энергетических единицах: n – число атомов в ряду, B – величина
магнитного поля, последний атом в ряду взаимодействует с первым (циклические граничные
условия Борна – Кармана [4]):
s
n+1
≡
s
1
. (3)
Форма записи матричных элементов в (1) такая же, как и для решетки с с двумя состояниями
узлов, отличие в том, что величины
s
k
могут принимать три значения, так что члены статистической
суммы образуют матрицу третьего порядка:

Вестник Северо-Кавказского государственного технического университета. 2011. № 1 (26)
11
,
ее
М
ее
θ−θ
−θ θ
⎛⎞
1
⎜⎟
=1 1 1
⎜⎟
⎜⎟
1
⎝⎠
(4)
причем под θ понимается либо θ
1
, либо θ
2
, в зависимости от направления взаимодействия.
Трансфер-матрицу P можно рассматривать как произведение трех матриц порядка 3
n
:
P = V
3
⋅V
2
⋅V
1
, (5)
где матрица V
3
описывает взаимодействие узлов решетки с магнитным полем, матрица V
2
описывает взаимодействие между рядами, матрица V
1
– взаимодействие в ряду.
По-видимому, для нахождения собственных значений трансфер-матрицы P следует каким-то
образом модифицировать метод Онсагера-Кауфман. До тех пор, пока этого не сделано для решетки
из узлов с тремя состояниями, большую помощь в поиске направления модификации метода может
оказать численное нахождение собственных значений трансфер-матрицы.
В
настоящей работе выполнен первоначальный этап решения задачи: разработан алгоритм
нахождения собственных значений и программа на языке Паскаль, а также приведены результаты
численных расчетов собственных значений для определенных значений параметров взаимодействия
и магнитного поля.
Чтобы иметь возможность изменять число атомов в ряду, был использован алгоритм
с задаваемым числом вложенных циклов [5]. Т. к
. трансфер-матрица задавалась в симметричной форме,
для диагонализации матрицы был использован метод вращений Якоби [6].
Детерминанты матриц V
3
и V
1
равны 1, детерминант матрицы V
2
, определяющей
взаимодействие между рядами, равен (2 sh 2θ
2
– 4 sh θ
2
)
n
. Поэтому имеет смысл нормировать
собственные значения, вынеся из каждого из них множитель (2 sh 2θ
2
– 4 sh θ
2
)
1/3
, тогда
произведение нормированных собственных значений будет равно 1, а сумма их логарифмов равна
нулю. Этот множитель равен кубическому корню из детерминанта матрицы (4), если в ней заменить
θ
на
θ
2
.
Программа нахождения собственных значений трансфер-матрицы P на языке Паскаль:
program Ising3sf; {Запись в файл}
{$S+,F-,I+,N-,R+,V-,D-}
Uses Crt,Dos;
type pp=array[1..9510] of real;
var nc2,ij,
nc,kpech,i,j,n,b,h,k:integer;
w,v,d,ik,i1,km :integer;
te1,te2,abeta,b1,b2,
s,b3,b4,e,mn :real;
k1 :array[1..18] of integer;
a :pp;
lst:text;
fgh:string;
label m1,m2,m3,m4,m5;
procedure formatr(te1,te2,abeta,b1,b2,b3,b4:real; var s:real);
begin
s:=s+0.5*abeta*(b1+b3);
s:=s+0.5*te1*(b1*b2+b3*b4);
s:=s+te2*b1*b3;
end{formatr};
procedure formatr3(te1,te2,te3,abeta,b1,b2,b3,b4,
b5,b6:real; var s:real);
begin
s:=s+0.5*abeta*(b1+b4);
s:=s+0.5*te1*(b1*b2+b4*b5);
s:=s+0.5*te2*(b1*b3+b4*b6);
