Вестник Северо-Кавказского государственного технического университета 2011 №1 (26)

Подождите немного. Документ загружается.

Вестник Северо-Кавказского государственного технического университета. 2011. № 1 (26)

s:=s+te3*b1*b4;

end{formatr3};

procedure sob_zn(n,kpech,km:word;e:real;var a:pp);

var k2,b,i,j,w,v,d :word;

ab,sr,c,l,f,p,r:real;

label m1,m2;

begin

w:=n*(n+1) div 2; v:=w+n;

writeln(lst);

if km<>0 then begin

for b:=1 to w do write(lst,a[b]:10:6); writeln(lst);

end;

for b:=1 to n do begin

for i:=1 to n do begin

a[w+i]:=1;

end;

f:=0;

m1:for i:=1 to n do begin

a[v+i]:=0;

for j:=1 to i do begin

k2:=i*(i-1) div 2;

a[v+i]:=a[v+i]+a[k2+j]*a[w+j];

end;

for j:=1 to n-1 do begin

for i:=j+1 to n do begin

k2:=i*(i-1) div 2;

a[v+j]:=a[v+j]+a[k2+j]*a[w+i];

end;

p:=0;r:=0;

for i:=1 to n do begin

p:=p+a[v+i]*a[v+i];

r:=r+a[w+i]*a[v+i];

end;

l:=p/r;c:=sqrt(p);p:=0;

for i:=1 to n do begin

a[w+i]:=a[v+i]/c;

if abs(a[w+i])>=p then p:=abs(a[w+i]);

end;

if abs(p-f)>e then begin f:=p; goto m1; end;

writeln(lst,'L[',b:2,']=',l:14:7);

sr:=0;

for i:=1 to n do begin

ab:=a[w+i]; sr:=sr+ab*ab;

end;

sr:=sqrt(abs(l/sr));

for i:=1 to n do begin

a[w+i]:=sr*a[w+i];

end;

for i:=1 to n do begin

if kpech <> 0 then

write(lst,' Y[',i:3,']=',a[w+i]:12:7);

Вестник Северо-Кавказского государственного технического университета. 2011. № 1 (26)

a[w+i]:=a[w+i]/sr;

end;

if kpech <> 0 then writeln(lst);

if b=n then goto m2;

for i:=1 to n do begin

for j:=1 to i do begin

d:=i*(i-1) div 2;

d:=d+j;

a[d]:=a[d]-l*a[w+i]*a[w+j];

end;

m2:end;

end;

procedure sob_zn3(n,kpech,km:word;e,mn:real;var a:pp);

var k2,b,i,j,w,v,d :word;

ab,sr,c,l,f,p,r:real;

label m1,m2;

begin

w:=n*(n+1) div 2; v:=w+n;

writeln(lst);

if km<>0 then begin

for b:=1 to w do write(lst,a[b]:10:6); writeln(lst);

end;

for b:=1 to n do begin

for i:=1 to n do begin

a[w+i]:=1;

end;

f:=0;

m1:for i:=1 to n do begin

a[v+i]:=0;

for j:=1 to i do begin

k2:=i*(i-1) div 2;

a[v+i]:=a[v+i]+a[k2+j]*a[w+j];

end;

for j:=1 to n-1 do begin

for i:=j+1 to n do begin

k2:=i*(i-1) div 2;

a[v+j]:=a[v+j]+a[k2+j]*a[w+i];

end;

p:=0;r:=0;

for i:=1 to n do begin

p:=p+a[v+i]*a[v+i];

r:=r+a[w+i]*a[v+i];

end;

l:=p/r;c:=sqrt(p);p:=0;

for i:=1 to n do begin

a[w+i]:=a[v+i]/c;

if abs(a[w+i])>=p then p:=abs(a[w+i]);

end;

if abs(p-f)>e then begin f:=p; goto m1; end;

if mn > 0 then

Вестник Северо-Кавказского государственного технического университета. 2011. № 1 (26)

writeln(lst,'L[',b:2,']=',l:14:7,l/mn:14:7,ln(l/mn):14:7)

else

writeln(lst,'L[',b:2,']=',l:14:7);

sr:=0;

for i:=1 to n do begin

ab:=a[w+i]; sr:=sr+ab*ab;

end;

sr:=sqrt(abs(l/sr));

for i:=1 to n do begin

a[w+i]:=sr*a[w+i];

end;

for i:=1 to n do begin

if kpech <> 0 then

write(lst,' Y[',i:3,']=',a[w+i]:12:7);

a[w+i]:=a[w+i]/sr;

end;

if kpech <> 0 then writeln(lst);

if b=n then goto m2;

for i:=1 to n do begin

for j:=1 to i do begin

d:=i*(i-1) div 2;

d:=d+j;

a[d]:=a[d]-l*a[w+i]*a[w+j];

end;

m2:end;

end;

begin

writeln('Введите имя файла');

readln(fgh);

assign(lst,'Ising'+fgh+'.txt');

rewrite(lst);

writeln('Введите NC,E,KPECH,KM,TE1,TE2,ABETA');

writeln;

WRITELN('NC-число узлов в ряду,E-точность,kpech,km-печ.соб.век.и матр.');

writeln('TE1,TE2,ABETA-пар.вз.верт.и гориз.и магн.поле');

read(nc,e,kpech,km,te1,te2,abeta);

writeln(lst,'Ising3sf.PAS');

writeln(lst,'Вычисление соб.зн.2-мерн.матр.Онсагера 3 сост.в магн.поле');

writeln(lst,'NC,E,KPECH,KM,TE1,TE2,ABETA=');

writeln(LST,NC:3,E:12:9,KPECH:3,km:3,TE1:8:3,TE2:8:3,ABETA:8:3);

writeln(lst);

writeln(lst,' N соб.зн. соб.зн/m ln(соб.зн./m)');

s:=exp(2*te2)-exp(-2*te2)-2*exp(te2)+2*exp(-te2);

s:=exp(ln(s)/3);mn:=1;

n:=1;

for i:=1 to nc do begin n:=n*3; mn:=mn*s;end;

h:=0;nc2:=2*nc;

for ij:=1 to nc2 do k1[ij]:=-1;

m3:i:=0;j:=0;

for ij:=1 to nc do begin

i:=3*i+k1[ij];j:=3*j+k1[ij+nc];

end;

Вестник Северо-Кавказского государственного технического университета. 2011. № 1 (26)

if j>i then goto m1;

h:=h+1;s:=0;

for ik:=1 to nc-1 do begin

b1:=k1[ik];b2:=k1[ik+1];

b3:=k1[ik+nc];b4:=k1[ik+nc+1];

formatr(te1,te2,abeta,b1,b2,b3,b4,s);

end;

b1:=k1[nc];b2:=k1[1];

b3:=k1[nc2];b4:=k1[nc+1];

formatr(te1,te2,abeta,b1,b2,b3,b4,s);

a[h]:=exp(s);

m1:i1:=nc2+1;

m4:i1:=i1-1;

if i1<1 then begin

sob_zn3(n,kpech,km,e,mn,a); goto m5;

end;

k1[i1]:=k1[i1]+1; if k1[i1]>1 then goto m2;

goto m3;

m2:k1[i1]:=-1; goto m4;

m5: close(lst);

end.

Таблица 1 – Натуральные логарифмы собственных значений матрицы взаимодействия, θ

=0,652; θ

=0,273

Магнитное поле β

Номер

0,000 0,001 0,01 0,1

1 4,7454529 4,7454557 4,7457317 4,7727283

2 3,6825049 3,6825026 3,6822813 3,6607612

3 1,9676520 1,9676524 1,9676902 1,9714734

4 1,1145562 1,1145562 1,1145495 1,1138727

5 -0,4682897 -0,4682898 -0,4683062 -0,4699381

6 -0,9415406 -0,9415406 -0,9415384 -0,9413215

7 -1,9102152 -1,9102155 -1,9102421 -1,9129009

8 -2,8033623 -2,8033625 -2,8033840 -2,8055353

9 -5,3867582 -5,3867585 -5,3867821 -5,3891399

1 6,9462240 6,9462302 6,9468440 7,0050067

2 6,0681345 6,0681298 6,0676650 6,0244868

3 4,5003035 4,5003047 4,5004230 4,5122006

4 4,5003035 4,5003047 4,5004230 4,5122006

5 4,0022270 4,0022269 4,0022223 4,0016623

6 2,8883432 2,8883428 2,8883016 2,8842346

7 2,8883432 2,8883428 2,8883016 2,8842346

8 1,6741387 1,6741384 1,6741112 1,6715436

9 1,6506744 1,6506751 1,6507415 1,6573544

10 1,6506744 1,6506751 1,6507415 1,6573544

11 1,5462800 1,5462806 1,5463351 1,5516123

12 0,3113154 0,3113150 0.3112715 0,3069458

13 0,3113154 0,3113150 0.3112715 0.3069458

14 0,1495554 0,1495550 0,1495080 0,1448484

15 -0,3454997 -0,3454998 -0,3455090 -0,3464280

16 -0,3454997 -0,3454998 -0,3455090 -0,3464281

17 -0,6520000 -0,6520000 -0,6520000 -0,6520000

18 -1,2816822 -1,2816826 -1,2817235 -1,2858214

19 -1,9772891 -1,9772895 -1,9773294 -1,9813190

20 -1,9772891 -1,9772895 -1,9773294 -1,9813190

21 -3,2137285 -3,2137287 -3,2137408 -3,2149602

22 -3,2137285 -3,2137287 -3,2137408 -3,2149602

23 -3,3192828 -3,3192828 -3,3192909 -3,3201005

24 -4,5309596 -4,5309600 -4,5309998 -4,5349810

25 -5,1181192 -5,1181196 -5,1181583 -5,1220282

26 -5,1181192 -5,1181196 -5,1181583 -5,1220282

27 -7,9946351 -7,9946354 -7,9946714 -7,9982572

Внимательное изучение таблицы результатов позволяет сделать заключение о существовании

для решетки с тремя возможными состояниями узлов формул, аналогичных формулам решетки с

двумя возможными состояниями.

Вестник Северо-Кавказского государственного технического университета. 2011. № 1 (26)

Литература

1. Onsager, L. Crystal statistics. I. A two-dimensional model with an order-disorder transition / L. Onsager // Phys.

Rev. 1944. Vol. 65. P. 117 – 149.

2. Kaufman, B. Crystal statistics. II. Partition function evaluated by spinor analysis / B. Kaufman // Phys. Rev. 1949.

Vol. 76. P. 1232 – 1243.

3. Ратнер, И. М. Математическое моделирование двумерной решетки Изинга в магнитном поле / И. М. Ратнер

// Инфотелекоммуникационные технологии в науке, производстве и образовании / Первая международная научно-техн.

конф. Ставрополь, 2004. С. 507 – 514.

4. Займан, Дж. Принципы теории твердого тела / Дж. Займан. – М. : Мир, 1974. – 472 с.

5. Ратнер, И. М. Алгоритм с задаваемым

числом вложенных циклов / И. М. Ратнер // Материалы V регион.

научно-техн. конф. Вузовская наука – Северо-Кавказскому региону ; ч. II. Ставрополь : СевКавГТУ 2001, С. 26 – 27.

6. Фаддеев, Д. К. Вычислительные методы линейной алгебры / Д. К. Фаддеев, В. Н. Фаддеева. – М. – Ленинград :

ФИЗМАТГИЗ, 1963. – 736 с.

References

1. Onsager, L. Crystal statistics. I. A two-dimensional model with an order-disorder transition / L. Onsager // Phys.

Rev. 1944. Vol. 65. P. 117 – 149.

2. Kaufman, B. Crystal statistics. II. Partition function evaluated by spinor analysis / B. Kaufman // Phys. Rev. 1949.

Vol. 76. P. 1232 – 1243.

3. Rathner, I. M. Mathematical modeling of two-dimensional Easing’s lattice in magnetic field / I. M. Ratner //

Infotelecommunication technologies in science, production and education / The first international scientific-practical conference,

Satvropol, 2994. P. 507 – 514.

4. Zaiman, J. Princicples of solid theory / J. Zaiman. – М. : Mir, 1974. – 472 p.

5. Rathner, I. M. Algorithm with enclosed cycles set numbers / I. M. Rathner // Materials of the V-th regional

scientific-practical conference. Higher education institute’s science for North Caucasus region ; part II. Stavropol : NCSTU,

2001. P. 26 – 27.

6. Faddeev, D. K. Calculation methods of linear algebra / D. K. Faddeev, V. N. Faddeeva. – M. – Leningrad :

FIZMATGIZ, 1963. – 736 p.

УДК 54.06

МЕТОДИКА ИССЛЕДОВАНИЯ ГИДРОГЕНИЗИРОВАННОГО КАРБИДА КРЕМНИЯ

МАСС-СПЕКТРОМЕТРИЕЙ ВТОРИЧНЫХ НЕЙТРАЛЬНЫХ ЧАСТИЦ

Сидоров К. И., Лисицын С. В., Зубрилов В. Г., Пигулев Р. В., Валюхов Д. П.

Представлена методика исследования гидрогенизированного карбида кремния (α-SiC:H) методом масс-

спектрометрии вторичных нейтральных частиц (SNMS) и обработки полученных спектров. Установлено кластерное

строение плёнки, соотношение между основными элементами образца и распределение водорода среди его

компонентов.

The technique of hydrogenated silicon carbide (α-SiC:H) study by a method of secondary neutral particles (SNMS)

mass spectrometry and processing of obtained spectra is presented. It was proved cluster film structure, ratio between sample

basic elements and hydrogen distribution among its components.

Ключевые слова: плёнка, аморфные полупроводники, карбид кремния, масс-спектрометрия вторичных

нейтральных частиц.

Key words: thin film, amorphous semiconductors, silicon carbide, mass spectrometry of secondary neutral particles.

В последние годы всё больший интерес проявляется к аморфным материалам в связи

с возможностью их использования при изготовлении солнечных батарей, датчиков давления

и температуры, элементов силовой и СВЧ-электроники. Данные материалы обладают ближним

порядком, поэтому способны обладать более разнообразными свойствами, чем монокристаллические

материалы. Однако описание их свойств в зависимости от состава

и структуры является более

сложным. В общем случае строение такого материала можно представить как совокупность хаотично

расположенных кластеров различного состава и структуры [1].

В работе представлена методика исследования аморфных полупроводников на примере

карбида кремния методом масс-спектрометрии вторичных нейтральных частиц. Измерения

проводились на спектрометре Micromass PC-100 при давлении порядка 5·10

-5

торр. Величина

ускоряющего напряжения ионного пучка Ar

была постоянна и составляла 4 кВ [2]. Для

исследования был выбран образец, синтезированный при температуре T = 950 °C

из триметилхлорсилана (ТМХС), методом химического осаждения из газовой фазы (ХОГФ).

Анализ результатов предварительных исследований показал, что карбид кремния распыляется

либо в виде отдельных атомов составляющих элементов, либо в виде целой молекулы SiC, а также в

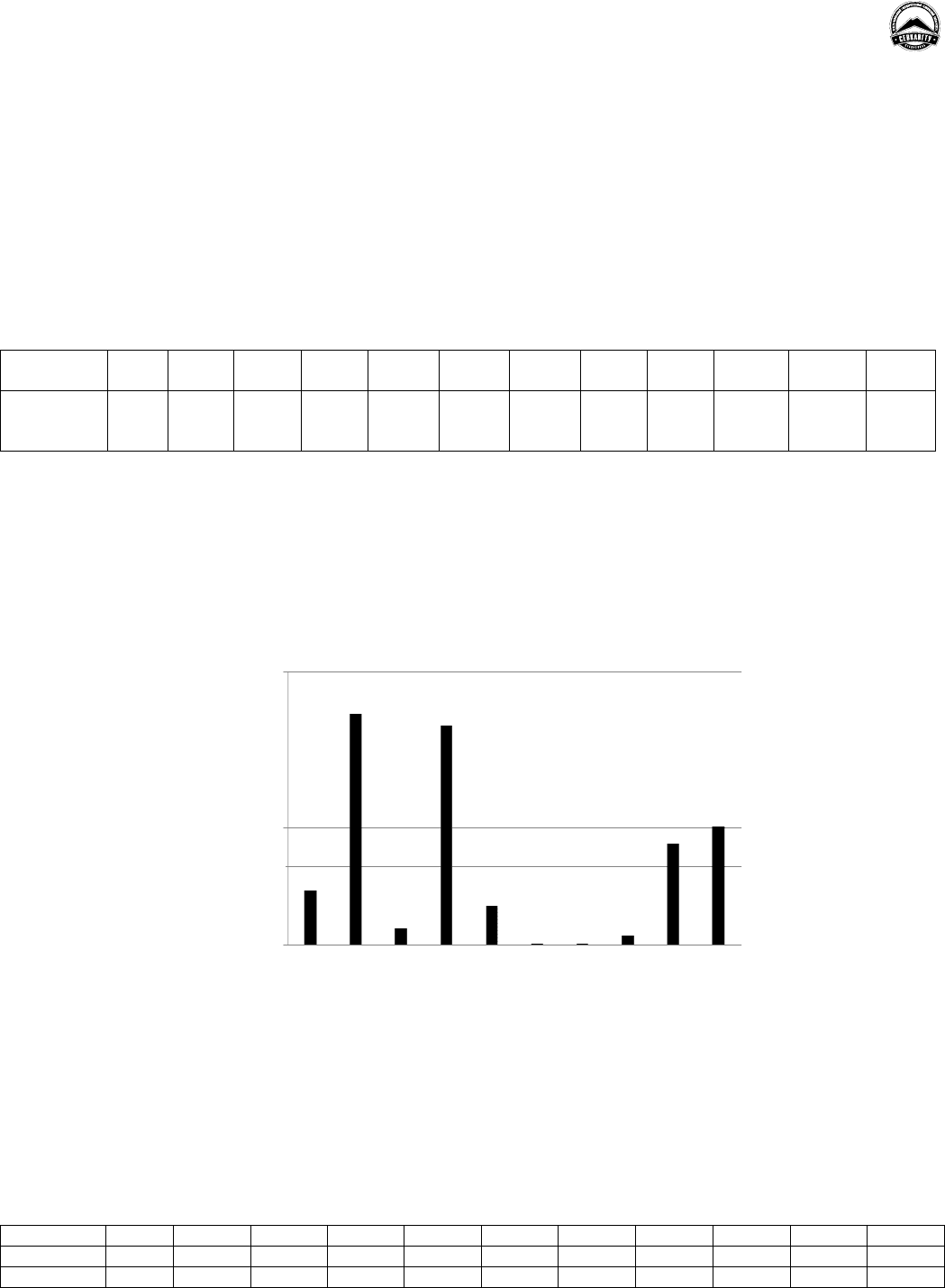
Вестник Северо-Кавказского государственного технического университета. 2011. № 1 (26)

виде кластеров типа SiCH

, C

, где n – число атомов водорода от одного до семи, q – число атомов

углерода в кластере от одного до трёх. Поэтому производился ионный мониторинг по каждому из

данных компонентов плёнки. Так как поток атомов, выбиваемых из образца, на три порядка больше

величины натекания газов из атмосферы, то их вклад в масс-

спектре можно не учитывать.

Основная сложность при обработке результатов заключалась в том, что атомная масса

кремния (Si) совпадает с молекулярной массой кластера С

, а молекулярная масса карбида

кремния (SiC) – с атомной массой аргона (Ar). Для решения этой проблемы, помимо основных

элементов, отслеживались их стабильные изотопы, а затем производился перерасчёт необходимых

элементов с учётом количественных соотношений между изотопами.

В таблице 1 представлены удельные массы, по которым производился ионный мониторинг,

и соответствующие им комбинации кластеров.

Таблица 1 – Удельные массы и соответствующие им компоненты плёнки

Удельная

масса

12 13 14 15 28 29 30 36 40 41 42 43

Компонент

плёнки

СН,

СН

Si,

SiH,

Si,

SiH

SiC,

SiCH,

SiCH

Как видно из таблицы 1, на некоторые удельные массы приходится до трёх вариантов

интерпретации возможных компонентов плёнки. Травление образца происходит послойно, поэтому

закономерности распыления монослоев углерода в плёнке SiC будут схожи с закономерностями

распыления углеродной плёнки при одинаковых условиях исследования (рабочий газ, параметры

первичного ионного пучка). Применяя поправочный коэффициент, учитывающий влияние кремния

на углеродные компоненты в SiC, можно оценить долю кластеров типа C

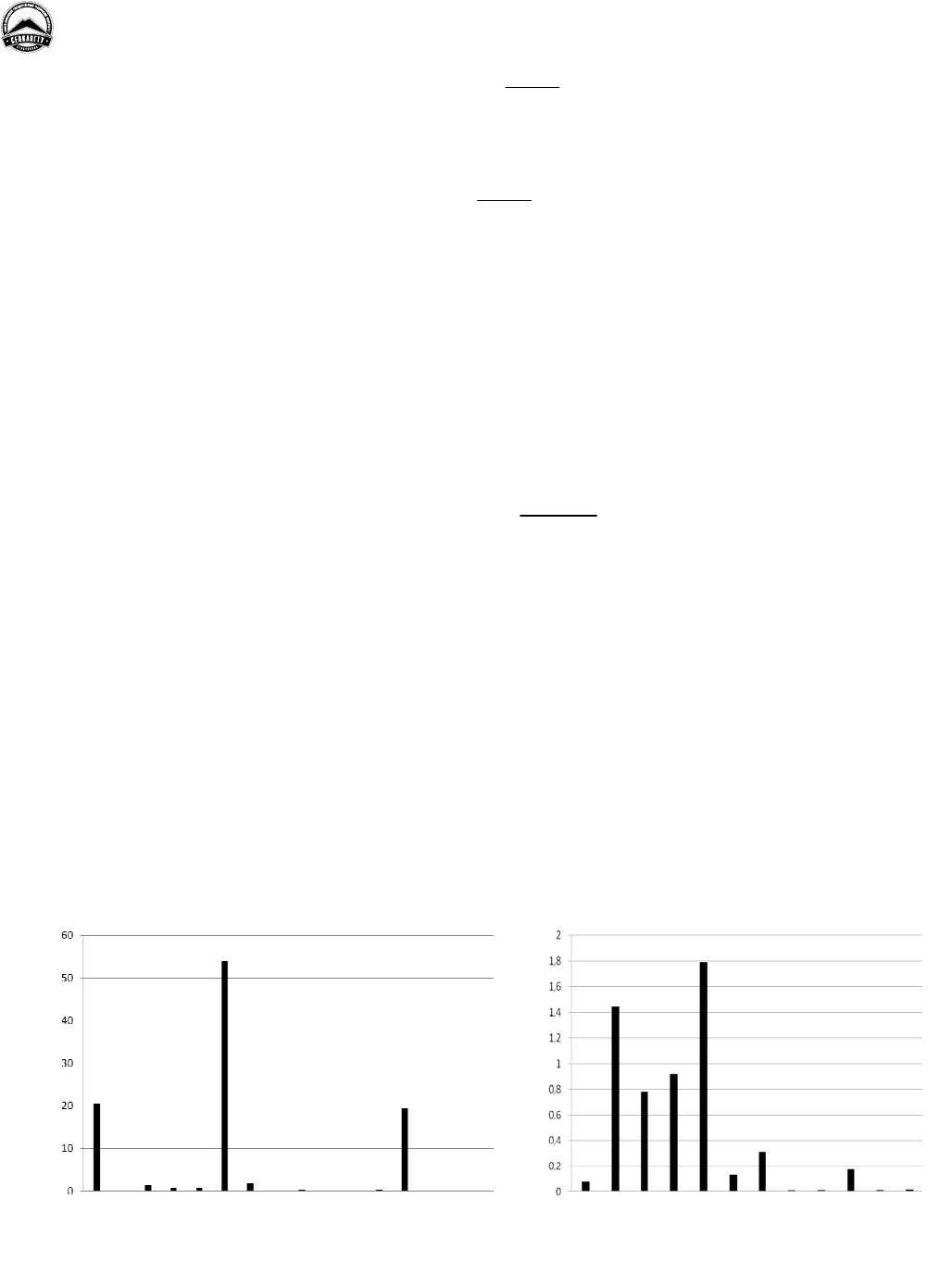
в масс-спектре. На рис.

1 представлена гистограмма гидрогенизированной плёнки углерода.

Рисунок 1 – Гистограмма компонентов плёнки α-С:Н

Помимо атомарного углерода происходит также распыление кластеров типа C

, с

преобладанием С

(порядка 90 %, для удобства оценки других компонентов не указан на

рисунке). Значения величин C

/С для гидрогенизированного углерода и карбида кремния

представлены в таблице 2.

Таблица 2 – Отношение C

/С для α-С:Н и α-SiC:H

Компонент C CH CH

α-С:Н 1 0,047

0,46 0,54 31,8 1,05 0,078 0,18 0,007 0,008 0,25

α-SiС:Н 1 0,055 0,54 0,63 37,4 1,24 0,092 0,21 0,008 0,01 0,29

Количество атомарного углерода в распыляемом потоке определяется согласно формуле:

Компоненты плёнки

Со

жание в об

аз

3,5

2,5

1,5

0,5

Вестник Северо-Кавказского государственного технического университета. 2011. № 1 (26)

0,989

C =

, (1)

где

S – величина сигнала с удельной массой равной 12.

Зная содержание C, можно рассчитать содержание кластеров C

по следующим формулам:

0,011

0,989

CH S=− ⋅

qn i

С HkC

, (2, 3)

где k

– соответствующий коэффициент из таблицы 2.

Далее производим расчёт по Si:

Si S C H=− . (4)

После определения доли кремния и зная соотношения между его изотопами, рассчитаем

содержание кластеров SiH, SiH

по следующим формулам:

SiHCSSiH ⋅−−= 045,0

; (5)

226

0,031SiH S C H Si

−−⋅. (6)

Для распыления плёнок используется Ar, который имеет стабильный изотоп с атомной массой

36, соответственно появляется возможность определения из сигнала

S доли молекулярного SiC:

0,00337

SiC S=−

. (7)

Последним этапом определяем содержание кластеров SiCH, SiCH

, SiCH

по следующим

формулам:

SiCH S C H=− ; (8)

236

SiCH S C H=− ; (9)

337

SiCH S C H=−

. (10)

Результаты расчёта представлены на рис. 2. К основным частям распыляемой плёнки

относится кластер C

, молекулярный SiC и Si. На все остальные компоненты плёнки приходится

чуть более 6 % от общего количества.

Для наглядности, неосновные компоненты вынесены на отдельную гистограмму (рис. 2 б).

В рисунок не были включены сведения о кластерах SiH и SiH

в виду их малого содержания

относительно других компонентов.

а б

Рисунок 2 – Гистограмма плёнки α-SiC:H общая (а), компоненты с малой долей в образце (б)

Таким образом, большая часть водорода содержится в углеродной части плёнки

гидрогенизированного карбида кремния. При данных условиях синтеза доля углерода в образце

преобладает над кремнием, значение, полученное в результате расчета C/Si = 3,4. Соотношение C/Si

можно оценить по следующей формуле:

SiC CH C CH

Si SiCH SiCH

SiCH

Компоненты плёнки

CH C CH

SiCH SiCH

SiCH

Соде

жание в об

азце

Соде

жание в об

азце

Вестник Северо-Кавказского государственного технического университета. 2011. № 1 (26)

CSi

∑

, (11)

где k – количество углеродсодержащих компонентов образца, m – количество

кремнийсодержащих компонентов образца, n

и n

– количество атомов углерода и кремния

в соответствующих компонентах с долями X

и Y

Таким образом, в данной работе была рассмотрена методика исследования α-SiC:H методом

масс-спектрометрии вторичных нейтральных частиц. Были получены следующие результаты

выводы:

−

разработана методика исследования плёнок гидрогенизированного карбида кремния

методом SNMS, показана возможность использования данных о содержании изотопов

контролируемых элементов в плёнке при обработке масс-спектров;

−

основными элементами образца являются Si и C с преобладанием последнего, отношение

C/Si = 3,4;

−

помимо основных элементов, в составе плёнки наблюдаются кластеры вида C

, SiCH

либо их комбинации;

−

водород практически полностью находится в кластерах углеродных компонентов.

Литература

. Аморфные полупроводники и приборы на их основе / под общ. ред. Й. Хамакавы ; пер. с англ. – М. :

Металлургия, 1986. – 376 с.

2. Изучение свойств алюминийсодержащих гетероструктур на основе соединений A

III

/ С. В. Лисицын,

Д. П. Валюхов, И. М. Хабибулин, А. В. Благин // Вестник Северо-Кавказский государственный технический

университет. Сер. Физико-химическая. 2003. № 1. С. 72.

References

1. Amorphous semiconductors and devices on their basis / edited by I. Khamakava ; translated from English. – M. :

Metalurgy, 1986. – 376 p.

2. Study of aluminium content heterostructures properties on the basis of A

III

combination / S. V. Lisitsyn,

D. P. Valyukhov, I. M. Khabibulin, A. V. Blagin // Bulletin of NCSTU. Physico-chemical series. 2003. № 1. P. 72.

УДК 621.387.143

ИОННАЯ ОЧИСТКА ПОДЛОЖЕК МИКРОПЛАТ В УСТАНОВКЕ

ВАКУУМНОГО НАПЫЛЕНИЯ КАК АЛЬТЕРНАТИВА ХИМИЧЕСКОЙ ОЧИСТКЕ

Шевченко Е. Ф., Мартенс В. Я.

Плазменный эмиттер с улучшенным управлением распределения плотности тока по поверхности эмиттера

разработан и применен для ионной очистки подложек микроплат в установке вакуумного напыления на

производственном предприятии микроэлектроники. Отдельная группа подложек была подвергнута многостадийной

химической очистке согласно действующему на производстве технологическому процессу. Проведено сравнение

показателей эффективности ионной и химической очистки. Выполнены испытания

на гидрофильность и адгезионную

прочность пленок для всех очищенных подложек. Разработана улучшенная методика определения адгезионной

прочности пленок. Сделаны выводы о целесообразности использования ионной очистки подложек в процессе

производства микроплат в качестве альтернативы химической очистке.

It was designed a plasma emitter with improved control of current density distribution on emitter’s surface and it was

used for ion cleaning of microplates substrates in vacuum sputtering at manufacturing plant of microelectronics. A separate

group of substrates were subjected to multistage chemical cleaning according to technological process at this plant. It was

carried out the comparison of ion and chemical cleaning efficiency indices and tests on water receptivity and films adhesive

durability for all cleaned substrates have been done. The improved method system for film adhesion durability definition was

developed. Some conclusions concerning the substrate ion cleaning use expediency during the process of microplates production

as an alternative to a chemical cleaning were drawn by authors in this paper.

Ключевые слова: плазма газового разряда, плазменный эмиттер, очистка подложек, напыление

пленок,

тонкопленочные микроплаты.

Key words: gas discharge plasma, plasma emitter, substrate cleaning, film sputtering, thin-film microplates.

Введение

Известно использование газоразрядной плазмы и ионных пучков для очистки подложек [1, 2].

Замена химических реактивов, предназначенных для очистки, плазмой позволяет получить высокую

степень чистоты, сократить затраты реактивов и рабочего времени. Предпочтительна очистка

подложек в установке вакуумного напыления непосредственно перед напылением пленок в одном

Вестник Северо-Кавказского государственного технического университета. 2011. № 1 (26)

вакуумном цикле, что позволяет получить наилучшую адгезионную прочность пленок. Кроме того,

в этом случае нет необходимости приобретения автономной установки плазмохимического

травления и строгого соблюдения правил вакуумной гигиены при выгрузке/загрузке очищенных

подложек. Для проведения очистки непосредственно перед напылением пленок в установке

вакуумного напыления могут использоваться плазменные эмиттеры большой площади [3, 4].

Обычно в

процессе очистки плазменные эмиттеры работают в режиме эмиссии ионов, так как

в этом случае можно использовать как физическое распыление поверхности ионами, так

и химическое воздействие ионов (реактивная ионно-плазменная обработка [2]).

Цель настоящей работы состоит в проведении исследований, направленных на выявление

показателей эффективности ионной и химической очисток и обосновании целесообразности

использования

на производственном предприятии того или иного вида очистки.

Техника и методика эксперимента

Исследования проводились на производственном предприятии «ОАО Ставропольский

радиозавод «Сигнал». Использовались подложки микроплат СВЧ ГИС [5] «Поликор» размером

60 × 48 мм. Одна группа подложек микроплат прошла многостадийную химическую очистку

согласно действующему на производстве технологическому процессу, включающему спиртовое

обезжиривание, промывку в ультразвуковой ванне, нагревание в соляной кислоте и хромовом

растворе, промывку деионизованной водой и сушку

в центрифуге. Общее время технологического

процесса химической очистки составляет 180 мин. Другая группа подложек была подвергнута

ионной очистке в установке вакуумного напыления УВН-75 с помощью разработанного авторами

плазменного эмиттера ионов большой площади с улучшенным управлением распределением

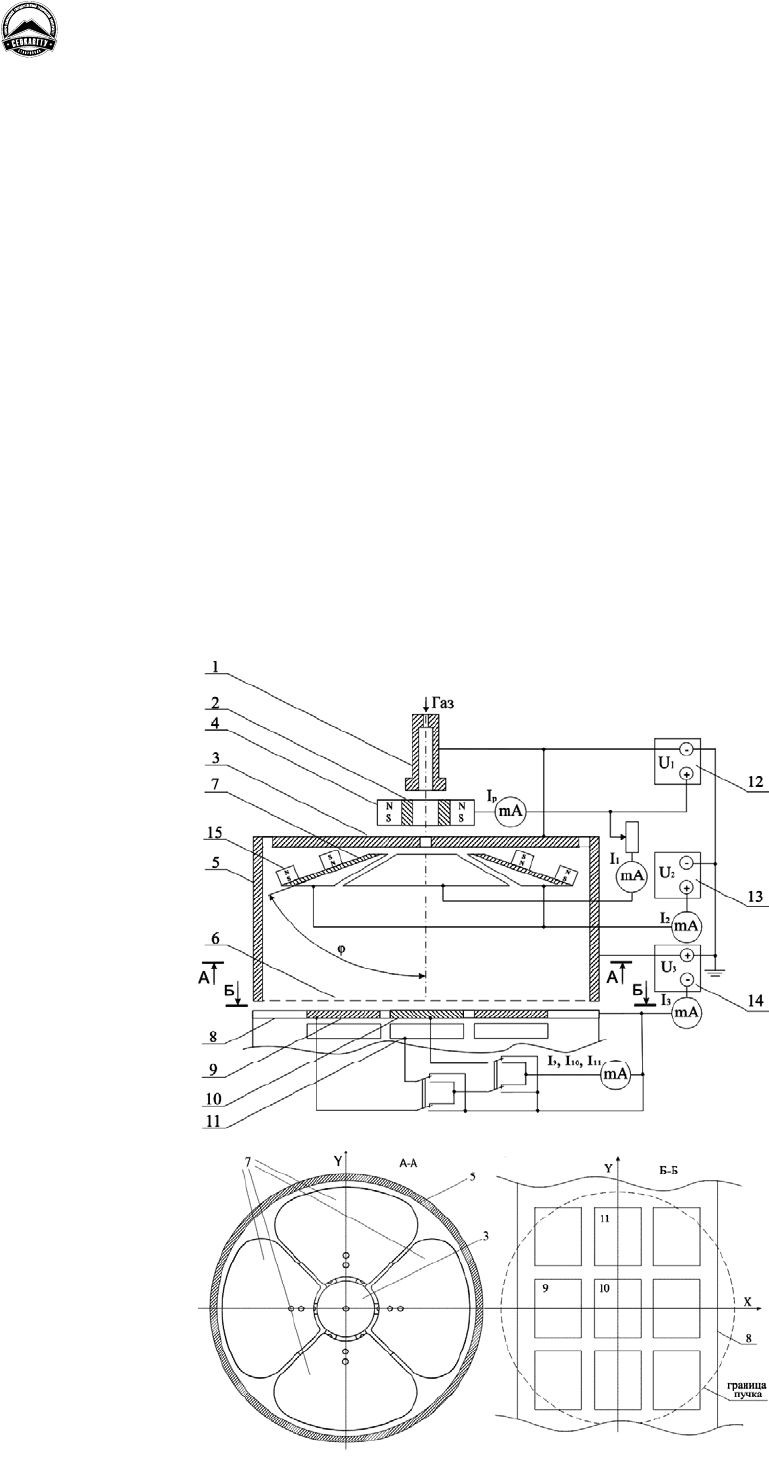
плотности тока по поверхности эмиттера (рис. 1).

______

Рисунок 1 – Схема плазменного эмиттера большой площади: 1 – полый катод, 2 – анод, 3 – катод-отражатель,

4 – кольцевой магнит, 5 – расширитель, 6 – эмиссионный электрод, 7 – электроды, 8 – карусель-подложкодержатель,

9, 10, 11 – подложки, 12, 13, 14 – источники электропитания, 15 – магниты

Вестник Северо-Кавказского государственного технического университета. 2011. № 1 (26)

Благодаря возможности управления распределением плотности тока по поверхности

эмиттера как по радиусу, так и по полярному углу, предложенный эмиттер позволяет формировать

пучки как круглого поперечного сечения диаметром 300 мм, так и пучки с другой формой сечения,

например, прямоугольного сечения без снижения энергетической эффективности. Это позволяет

эффективно использовать данный эмиттер в УВН-75 как

при вращающейся каруселе-

подложкодержателе 8 (пучок прямоугольного сечения), так и при неподвижной (пучок круглого

сечения), а также обеспечивает равномерную эмиссию ионов (неравномерность не превышала

± 10 %) и существенное уменьшение потери ионов на непрозрачном участке эмиссионного

электрода 6 (стальной пластине).

Технологическая операция ионной очистки проводилась ионным пучком прямоугольного

поперечного сечения размерами 220×60 мм в течении 10 мин

при напуске воздуха в полый катод

1 (рис. 1) и давлении в вакуумной камере 50 мПа. При этом электроды 7 устанавливались под углом

= 70º, ток вспомогательного разряда I

составлял 150 мА, токи на пары противоположных

электродов 7 составляли 150 и 350 мА, ток эмиссии ионов – 50 мА при ускоряющем напряжении

= 560 В.

Известно, что гидрофильность поверхности подложек – это важный критерий при оценке

степени чистоты, который позволяет получить информацию о присутствии на поверхности

гидрофобных органических загрязнителей [6]. Для теста на гидрофильность деионизованную воду

марки «А» распыляли над поверхностью подложек, прошедших различные виды очистки

и фиксировали растекаемость пленки воды на подложках через 60 с после

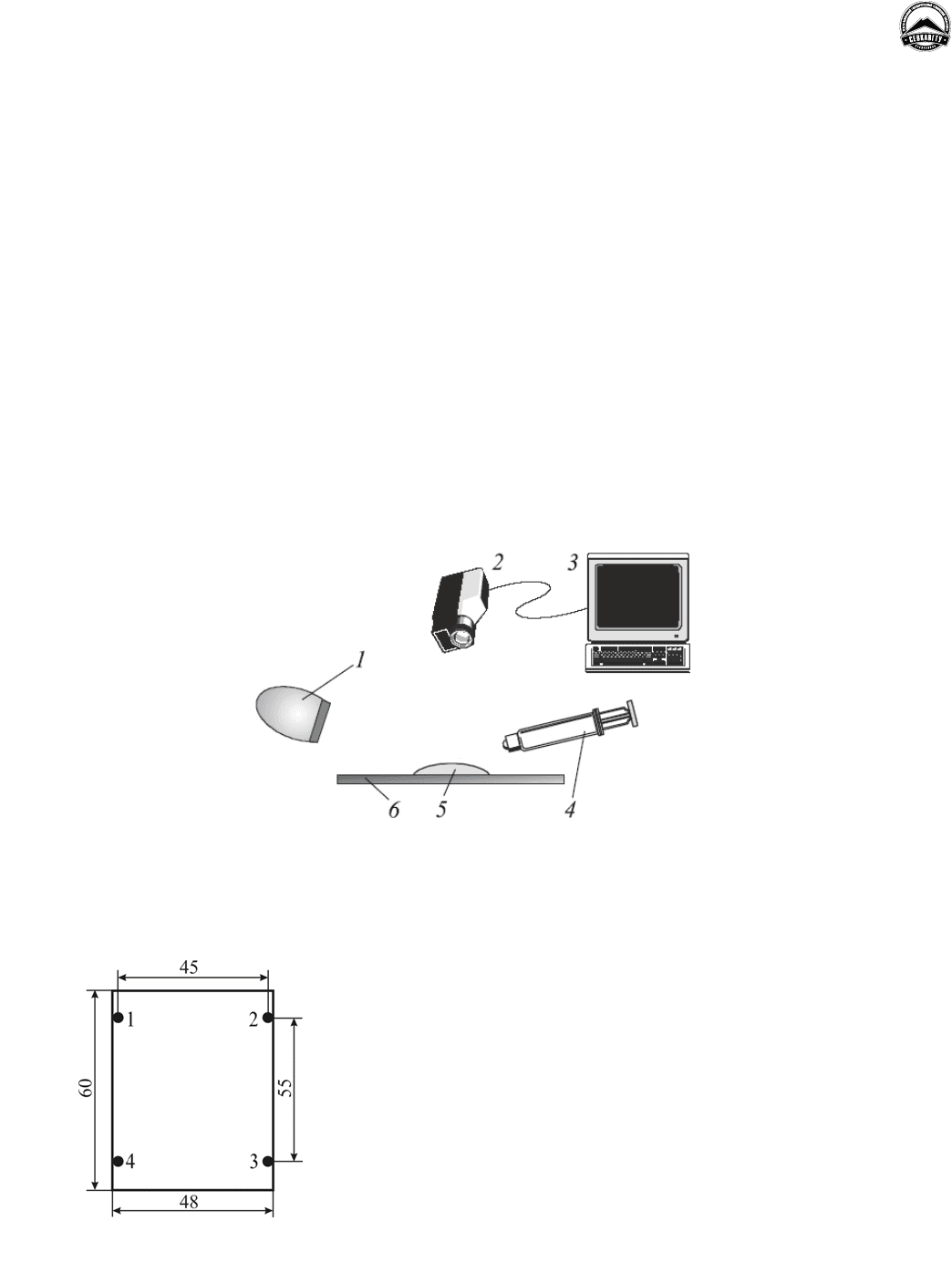
распыления воды (рис. 2).

Рисунок 2 – Схема проведения теста на гидрофильность: 1 – источник света, 2 – фотокамера, 3 – ПК для вывода

фотоснимков, 4 – распылитель воды, 5 – растекающаяся вода, 6 – подложки

На подложки, прошедшие очистку, производили напыление тонкопленочной структуры

микроплат РС3710-Сu методом магнетронного распыления. Пленка РС3710 играет роль

адгезионного и резистивного подслоя микроплаты.

Испытания адгезионной прочности пленок проводили

по разработанной нами методике, так как стандартные

методики, основанные на скрайбировании [7] или

нормальном отрыве заданного шаблоном участка пленки

известной площади, оказались неприменимы ввиду

очень

высокой адгезионной прочности пленок и твердости

подслоя РС-3710. В этих случаях получить эффект

скрайбирования не удавалось, а отрыв пленки с заданной

шаблоном площадью в ряде опытов оказывался

неполным, так как на подложке оставались неоторванные

«островки» покрытия. Разработанная нами методика для

определения высоких значений адгезионной прочности

сводилась к следующему. К

медному покрытию

на четырех краевых участках подожки (рис. 3) припаивали торцом отрезки провода и измеряли силу

нормального отрыва провода с участком тонкой пленки от подложки на динамометре МИП-10.

Использовались краевые участки покрытия, так как адгезионная прочность на них обычно меньше,

чем в центре. Данные, полученные в результате четырех опытов, усреднялись.

Рисунок 3 – Точки отрыва пленки 1 – 4

на краевых участках микроплаты