Вестник отделения строительных наук РААСН 2011 №15

Подождите немного. Документ загружается.

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

140

_________________________________________________________________________________________________________________

–

достижение

нормальными

напряжениями

осевого

направления

бетоне

ядра

значе

ния

прочности

бетона

при

трехосном

сжатии

= R

;

–

достижение

интенсивности

напряжений

наиболее

сжатом

волокне

стальной

обо

лочки

предельной

величины

соответствующей

критерию

Генки

Мизеса

(

pspi

);

–

достижение

нормальными

напряжениями

осевого

направления

наиболее

растяну

том

волокне

стальной

оболочки

расчетного

сопротивления

растяжению

Учитывая

внутреннюю

статическую

неопределимость

трубобетонной

конструкции

первое

условие

наступления

предельного

состояния

должно

выполняться

совместно

со

вто

рым

или

третьим

целью

обеспечения

эксплуатационной

пригодности

ТБК

при

действии

на

них

рас

четных

нагрузок

величины

деформаций

стальной

оболочки

(

наиболее

сжатом

волокне

–

интенсивность

деформаций

pi,

наиболее

растянутом

волокне

–

осевая

деформация

также

осевые

деформации

бетонного

ядра

bzu

должны

ограничиваться

соответствующими

значениями

Предельные

относительные

деформации

сжатого

бетона

при

двузначной

однознач

ной

неравномерной

эпюрах

деформаций

нормальном

сечении

принимаются

соответствии

методикой

СНиП

52-01-03.

Для

исключения

чрезмерных

деформаций

ТБК

предельные

от

носительные

деформации

bzu

во

всех

случаях

рекомендуется

ограничивать

величиной

0,006.

Предельное

значение

интенсивности

относительных

деформаций

наиболее

сжатого

участка

стальной

оболочки

относительной

деформации

удлинения

растянутого

участка

стальной

оболочки

max,pz

рекомендуется

назначать

следующим

образом

для

сталей

физической

площадкой

текучести

015,0

pspspu

;

для

сталей

условной

площадкой

текучести

025

,0=

Предложенная

универсальная

методика

расчета

позволяет

оценивать

не

только

проч

ность

но

напряженно

деформированное

состояние

ТБК

на

любом

уровне

их

загружения

Данная

методика

учитывает

физическую

нелинейность

компонентов

неоднородность

напряженного

состояния

процессы

перераспределения

усилий

между

стальной

оболочкой

ядром

Предложенный

подход

позволяет

достаточно

просто

учитывать

расчетах

колонн

стадии

возведения

несущих

конструкций

что

достаточно

важно

при

проектировании

высот

ных

зданий

Также

здесь

имеется

возможность

учета

практически

любого

варианта

армиро

вания

бетонного

ядра

ТБК

Основные

положения

этой

методики

могут

быть

использованы

при

расчете

различ

ных

конструкций

сжатых

элементов

косвенным

армированием

Библиографический список

KRISHAN, A L, Steel pipe-concrete columns with preliminary pressed core // Appli-

cations. Opportunities: Proceedings of the International Conference held at the University of Dun-

dee, Scotland, UK on 5-7 July 2005, pp 725-733.

Ильюшин

Пластичность

[

Текст

] /

Ильюшин

. –

Москва

Ленинград

Гос

техиздат

, 1948. – 372

Карпенко

Общие

модели

механики

железобетона

[

Текст

] /

Карпенко

. –

Стройиздат

, 1996. – 416

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

_________________________________________________________________________________________________________________

141

УДК

539.384.6

САМСОНЕНКО

ТРЕЩЕВ

(

Тульский

государственный

университет

Тула

)

ТЕРМОУПРУГИЙ ИЗГИБ КРУГЛЫХ ПЛАСТИН СРЕДНЕЙ

ТОЛЩИНЫ, ВЫПОЛНЕНЫХ ИЗ АН ИЗОТРОПНЫХ

РАЗНОСОПРОТИВЛЯЮЩИХСЯ МАТЕРИАЛОВ

Зависимость

деформационных

характеристик

от

вида

напряженного

состояния

для

конструкционных

материалов

достаточно

сложна

не

сводится

только

неодинаковому

их

поведению

при

одноосных

растяжении

сжатии

Экспериментально

установлено

что

жест

кость

большинства

анизотропных

разносопротивляющихся

материалов

может

зависеть

не

только

от

знаков

возникающих

напряжений

но

от

их

количественных

соотношений

тем

пературных

факторов

Классические

теории

базирующиеся

на

гипотезах

единых

кривых

»,

очевидно

не

мо

гут

правильно

оценить

напряженно

деформированные

состояния

пластин

средней

толщины

обладающих

указанными

особенностями

Полноценный

учет

свойств

разносопротивляемо

сти

анизотропии

знание

величины

характера

действия

температурных

напряжений

необ

ходимы

для

всестороннего

анализа

прочности

конструкции

Температурные

напряжения

сами

по

себе

сочетании

силовыми

напряжениями

от

внешней

нагрузки

могут

вызвать

появление

трещин

разрушение

конструкций

из

материа

лов

повышенной

хрупкостью

Из

всего

выше

сказанного

можно

сделать

вывод

том

что

учет

явления

разносопро

тивляемости

материалов

также

исследование

влияния

температуры

на

деформирование

пластин

является

актуальной

задачей

Предлагается

новая

математическая

модель

изгиба

пластин

средней

толщины

выпол

ненных

из

анизотропных

разносопротивляющихся

материалов

которая

учитывает

влияние

температуры

на

общее

напряженно

деформированное

состояние

Рассматривается

несвязан

ная

задача

термоупругости

вследствие

этого

задача

термоупругом

изгибе

пластин

распа

дается

на

две

независимые

задачи

механики

сплошной

среды

термодинамики

Такой

под

ход

позволяет

исследовать

температурное

поле

твердом

теле

соответствующее

определен

ным

условиям

теплопередачи

независимо

от

деформированного

состояния

тела

Однако

следует

заметить

что

влиянием

деформаций

тела

на

распределение

нем

температуры

мож

но

пренебречь

при

рассмотрении

материалов

для

которых

эффект

связанности

полей

де

формаций

температур

мал

Основываясь

на

работах

Матченко

Трещева

[2],

также

классических

со

отношениях

механики

были

получены

определяющие

соотношения

описывающие

поведе

ние

конструкционных

анизотропных

разносопротивляющихся

материалов

условиях

тер

момеханического

загружения

Полученные

соотношения

были

конкретизированы

для

задачи

термоупругого

изгиба

тонких

круглых

пластин

что

дальнейшем

позволило

сформулиро

вать

разрешающие

уравнения

изгиба

пластин

перемещениях

Рассмотрим

упругое

равновесие

круглой

пластины

средней

толщины

радиусом

r a

под

действием

поперечной

равномерно

распределенной

нагрузки

разницы

темпе

ратур

по

границам

пластинки

∆

Рассмотрим

случай

когда

пластинка

нагревается

по

верхностей

внутри

пластины

отсутствует

источник

тепла

температура

изменяется

только

по

ее

толщине

Положим

что

пластина

выполнена

из

анизотропных

разносопротивляющихся

материалов

обладающих

цилиндрической

ортотропией

Ввиду

осевой

симметрии

задачи

для

ее

решения

удобно

воспользоваться

цилиндрической

системой

координат

При

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

142

_________________________________________________________________________________________________________________

этом

функции

характеризующие

напряженно

деформированное

состояние

пластины

будут

зависеть

только

от

радиальной

координаты

Для

пластинки

средней

толщины

применим

гипотезы

Тимошенко

нормальное

срединной

плоскости

пластины

перемещение

(

прогиб

пластины

)

не

зависит

от

координаты

(

);

нормаль

срединной

плоскости

после

деформации

поворачивается

на

угол

от

носительно

оси

относительно

оси

;

при

определении

параметров

напряженного

состояния

влиянием

нормальных

на

пряжений

пренебрегаем

Используя

гипотезы

Тимошенко

учитывая

что

рассматривается

геометрически

ли

нейные

задачи

общем

случае

загружения

круглой

пластины

произвольной

нагрузкой

для

перемещений

деформаций

получим

( , ) ( ) ( )

u r z u r z r

= +

;

( , ) ( )

u r z w r

;

, ,

r r r

e u z

= +

;

/ /

e u r z r

θ θ

= +

;

,rz r

γ ψ

= +

. (1)

Уравнения

связи

деформаций

напряжениями

учетом

температурного

воз

действия

общем

случае

для

ортотропных

разносопротивляющихся

материалов

можно

при

нять

виде

[2],

добавив

температурные

компоненты

( )

ij ijkm qp km ij ij

e C T

ω σ α δ

= + ∆

, , , , , 1,2,3

i j k m q p

, (2)

где

kkkkkkkkkkkkkk

BAC

;

)(

jjiiiijjiijjiijj

BAC

ωω

++=

при

≠

, (

здесь

по

индексам

не

суммировать

);

)2(

ijiiiiijiiijiiij

BAC

ωω

++=

при

≠

;

ijijijijijijij

BAC

2+=

при

≠

;

)2(

jkiiiijkiijkiijk

BAC

ωω

++=

при

≠

;

)2(2

kmijijkmijkmijkm

BAC

ωω

++=

при

≠

;

kmijijkm

CC =

;

ij ij ij ij

= /

ω σ σ σ

;

∆

–

разность

температур

;

–

коэффициент

линейного

рас

ширения

материала

;

–

символ

Кронекера

ijkm

–

константы

подлежащие

определе

нию

из

экспериментов

по

деформированию

образцов

материала

Неизвестные

параметры

ijkm

следует

определять

через

технические

констан

ты

по

формулам

[2]:

2/)/1/1(

−+

kkkkkk

EEA

;

2/)/1/1(

−+

−=

kkkkkk

EEB

;

2/)//(

−−++

+−=

jijjijiijj

EEA

νν

;

2/)//(

−−++

−−=

jijjijiijj

EEB

νν

;

)]//(2)/1/1/1/1[(25,0)/1/1(

−−++−−++−+

+−+++−+=

ijiijijijiijijijij

EEEEEEEEA

νν

; (3)

)]//(4)/1/1/1/1[(2125,0)/1/1(2

−−++−−++−+

−−−−+−−=

ijiijijijiijijijij

EEEEEEEEB

νν

;

++++

ijijij

νν

;

−−−−

ijijij

νν

где

–

модули

упругости

при

растяжении

сжатии

направлениях

соответст

вующих

главных

осей

анизотропии

;

–

коэффициенты

поперечной

деформаций

при

растяжении

сжатии

соответствующие

главным

осям

анизотропии

;

–

модули

упругости

при

растяжении

сжатии

направлениях

под

углом

45°

соответствующим

главным

осям

анизотропии

Перепишем

уравнения

связи

деформаций

напряжений

учетом

температурных

де

формаций

для

рассматриваемой

пластинки

принятой

радиальной

системе

координат

TCCe

rrr

∆

11221111

;

TCCe

∆

θθθ

22221122

;

rzrz

1313

, (4)

где

–

коэффициент

линейного

расширения

материала

направлениях

Разрешим

зависимости

между

деформациями

напряжениями

(2)

относительно

на

пряжений

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

_________________________________________________________________________________________________________________

143

rrTrr

ReCeC

−

1211

;

θθθθ

ReCeC

−

2212

;

rzrzrz

ReC

−

, (5)

где

∆

222211

;

∆

111122

;

∆

−

112212

;

131313

/1 AC

;

12121111

TCTCR

;

11122222

TCTCR

;

1313

TCR

;

112222221111

AAA −=∆

;

)(

2211112211111111

BBT

;

BBT

)(

2211112222222222

;

τω

13131313

;

TCTC

rrT

∆

1211

;

TCTC

∆

θθ

2212

Таким

образом

зависимость

между

напряжениями

перемещениями

учетом

(5)

(1)

можно

представить

следующем

виде

rrTrrr

RrzruCzuC −−+++=

θψψσ

θθ

)//()(

12,,11

;

θθθθθ

θψψσ

RrzruCzuC

Trr

−−+++= )//()(

22,,12

; (6)

rzrrz

RwC −+= )(

,13

ψτ

Приведем

напряжения

(6)

их

интегральным

характеристикам

по

тради

ционным

формулам

[3]:

∫

−

dzN

;

∫

−

dzN

θθ

;

∫

−

zdzM

;

∫

−

zdzM

θθ

;

∫

−

rzr

dzQ

(7)

получим

rrTrr

IrhuChuCN −−+=

12,11

;

θθθ

IrhuChuCN

−−+= /

22,12

;

rrTrr

CM −−+=

χψψ

θθ

12,

;

θθθθθ

χψψ

−−+=

22,

; (8)

rzrr

IwhCQ −+= )(

,13

где

∫

−

dzRI

;

∫

−

dzRI

θθ

;

∫

−

zdzRJ

;

∫

−

zdzRJ

θθ

;

∫

−

rzrz

dzRI

;

∫

−

rTrT

θε

;

∫

−

θθ

θε

;

∫

−

rTrT

zdz

θχ

;

∫

−

zdz

θθ

θχ

Условия

равновесия

принимаются

виде

[3]:

0/)(

=−+ rNNN

rrr

;

qrQQ

rrr

−=+ /

;

0/)(

=−−+

rrrr

QrMMM

. (9)

Используя

эти

зависимости

(9)

выражения

для

усилий

моментов

(8),

получим

сис

тему

трех

нелинейных

дифференциальных

уравнений

относительно

функций

rrrTrTrrr

IrIIrrhuCrhuChuC

22,11,11

/)(/)(// +−=−−−+

θθ

εε

;

rrzrzrrrr

IrIqrrwwhC

,,,,13

/)//( ++−=+++

θθ

ψψ

; (10)

rzrrrTrTrrrr

IJrJJrhwChC

C −+−=−−−+−+

,,1313

22,

11,

/)(/)()

θθθθθ

χχψψψ

уравнениям

(10)

следует

присоединить

граничные

условия

при

(

)

виде

)

для

варианта

жесткого

защемления

;

; (11)

)

для

варианта

шарнирного

закрепления

;

rrTr

C =−+

χψψ

θθ

12,

; (12)

)

для

варианта

скользящей

заделки

;

rrTr

IrhuChuC =−+

12,11

; (13)

)

для

варианта

свободного

опирания

;

rrTr

C =−+

χψψ

θθ

12,

;

rrTr

IrhuChuC =−+

12,11

; (14)

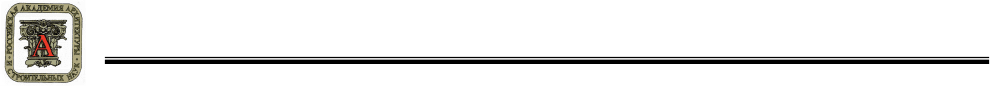
РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

144

_________________________________________________________________________________________________________________

Кроме

контурных

необходимо

также

привлекать

граничные

условия

центре

пласти

ны

при

;

. (15)

Для

определения

температурных

компонентов

из

уравнений

(10)

необходимо

решить

отдельно

задачу

передачи

тепла

через

поверхность

пластины

Процесс

теплопередачи

можно

описать

классическим

уравнением

теплопроводности

Для

одномерного

случая

уравнение

теплопроводности

можно

записать

виде

zzt

TaT

)()( ∂=∂

, (16)

где

–

ось

системы

координат

перпендикулярная

поверхности

пластины

;

–

темпера

турное

поле

;

a c

–

коэффициент

температуропроводности

характеризирующий

тепло

инерционные

свойства

тела

;

–

удельная

объемная

теплоемкость

тела

Для

однозначности

решения

уравнения

теплопроводности

необходимо

его

дополнить

начальными

граничными

условиями

качестве

начального

условия

задается

распределение

температуры

тела

момент

времени

Это

распределение

зачастую

принимается

равномерным

constTzT

)0,(

. (17)

уравнению

теплопроводности

(16)

следует

присоединить

граничные

условия

Гра

ничные

условия

связаны

со

сложным

теплообменом

на

поверхности

тела

где

могут

иметь

место

различные

способы

теплопередачи

одновременно

Наиболее

просто

эффективно

качестве

граничных

условий

можно

задать

распре

деление

температуры

по

поверхности

пластинки

),(),( tzftzT

, (18)

где

),( tzf

–

заданная

функция

распределения

температурного

поля

Таким

образом

уравнения

(10)

(16)

представляют

собой

полную

разрешающую

сис

тему

уравнений

достаточную

для

исследования

напряженно

деформированного

состояния

круглых

пластин

средней

толщины

выполненных

из

ортотропных

разносопротивляющихся

материалов

при

термоупругом

изгибе

Полученные

уравнения

изгиба

круглых

анизотропных

пластин

средней

толщины

вы

полненных

из

материалов

чувствительных

виду

напряженного

состояния

широким

диа

пазоном

изменения

механических

характеристик

температурных

градиентов

могут

быть

использованы

для

прочностных

жесткостных

расчетов

широкого

круга

конструктивных

элементов

химической

промышленности

авиастроительной

машиностроительной

строи

тельной

отраслях

Библиографический список

Коваленко

Термоупругость

[

Текст

Коваленко

;

Издательское

объедине

ние

Вища

школа

», 1975. – 216

Матченко

Теория

деформирования

разносопротивляющихся

материалов

Оп

ределяющие

соотношения

[

Текст

] /

Матченко

Трещев

;

Тула

ТулГУ

, 2000. – 149

Тимошенко

Пластинки

оболочки

[

Текст

] /

Тимошенко

Войнвский

Кригер

. –

Наука

, 1966. – 636

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

_________________________________________________________________________________________________________________

145

УДК

624.042.12

ТАМРАЗЯН

(

Московский

государственный

строительный

университет

Москва

)

ОСОБЕННОСТИ РЕОЛОГИЧЕСКОГО МОДЕЛИРОВАНИЯ ДЛЯ

РАСЧЕТА КОНСТРУКЦИЙ ИЗ ВЫСОКОПРОЧНЫХ БЕТОНОВ

Современные

тенденции

изменения

или

придания

тех

или

иных

свойств

бетонам

без

учета

их

пригодности

адекватной

оценки

при

различных

режимах

нагружения

от

мгновен

но

динамического

до

длительных

требует

также

разработки

адекватных

моделей

учиты

вающих

эти

изменения

Исследованию

реологических

свойств

высокопрочных

бетонов

(

классов

выше

)

при

длительном

нагружении

посвящено

мало

работ

их

еще

предстоит

изучить

Быстрый

набор

прочности

смеси

довольно

высокой

подвижностью

дальнейшее

старение

сопрово

ждающееся

изменением

вязкостных

свойств

модулей

упругости

является

одной

из

особенностей

высокопрочных

бетонов

качестве

основных

решений

для

таких

бетонов

мо

жет

быть

использовано

реологическое

моделирование

вязко

упругих

тел

наследственного

старения

[1].

Вязкоупругое

деформирование

под

длительно

действующими

внешнесиловыми

воз

действиями

является

основной

реологической

природой

бетонов

частности

для

расчета

железобетонных

конструкций

разработаны

разные

теории

вязкоупругости

(

ползучести

ко

торые

развиваются

трех

основных

направлениях

теория

упругой

наследственности

теория

старения

наследственная

теория

старения

Теория

упругой

наследственности

своей

основе

имеет

интегральное

уравнение

Вольтерра

второго

рода

ядро

которого

представляет

аналитическую

функцию

разности

ар

гументов

времени

)(

),(

τα

ατ

−−

ECetK

, (1)

где

–

момент

наблюдения

процесса

;

–

начало

процесса

Тот

факт

что

основных

интегро

дифференциальных

уравнениях

состояния

фигури

рует

разность

−

говорит

том

что

оценка

процесса

имеет

инвариантный

характер

по

от

ношению

началу

времени

отчета

Это

значит

что

явление

характеризуется

своей

наследст

венностью

значение

возраста

материала

как

один

из

определяющих

факторов

игнориру

ется

Очевидно

что

такая

теория

на

феноменологическом

уровне

может

отражать

поведение

лишь

только

тех

материалов

физико

механические

свойства

которых

со

временем

не

пре

терпевают

изменений

не

стареющих

материалов

либо

достаточно

взрослых

материалов

Однако

известно

что

вязкостные

свойства

наиболее

ярко

проявляются

именно

стареющих

материалах

особенно

молодом

возрасте

что

делает

теорию

упругой

наследственности

наиболее

уязвимой

для

приложения

Математический

аппарат

теории

упругой

наследственности

обоснован

нестареющей

реологической

моделью

Кельвина

[2, 3].

отличие

от

теории

упругой

наследственности

основу

вязкоупругой

теории

старения

составляют

исключительно

возрастные

характеристики

бетонов

вовсе

отсутствуют

на

следственные

признаки

Это

приводит

тому

что

кривые

вязкоупругости

(

ползучести

)

для

разных

возрастов

начала

загружений

одного

того

же

материала

согласно

этой

теории

па

раллельны

Такая

трактовка

явления

ползучести

приводит

другой

крайности

Согласно

тео

рии

старения

вполне

взрослые

(

старые

)

бетоны

не

проявляют

вязко

ползучие

свойства

что

не

соответствует

действительности

Математический

аппарат

теории

старения

своей

основе

не

имел

реологическую

мо

дель

старения

тел

что

не

позволило

оценить

диссипативные

процессы

определить

динами

−

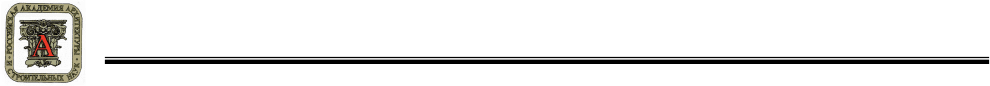
РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

146

_________________________________________________________________________________________________________________

ческие

характеристики

стареющих

сред

на

основе

этой

теории

Для

устранения

этого

пробе

ла

была

предложена

вязкоупруго

стареющая

модель

которая

полностью

отражает

механиче

ское

поведение

взрослеющих

материалов

на

основе

теории

старения

[4, 5].

Синтезом

теории

упругой

наследственности

теории

старения

является

наиболее

строгая

феноменологическая

теория

вязкоупругости

–

наследственная

теория

старения

Ос

новные

интегро

дифференциальные

уравнения

этой

теории

на

должном

уровне

отражают

как

наследственные

так

возрастные

признаки

материалов

Поэтому

наследственная

теория

старения

является

наиболее

приемлемой

феноменологической

теорией

для

оценки

поведения

вязкоупруго

стареющих

сред

Основы

наследственной

теории

старения

положены

Масловым

[6]

Арутю

няном

[2].

Она

получила

свое

развитие

трудах

Александровского

[7],

Бондаренко

[8],

Гвоздева

Галустов

[9],

.A.

Карапетяна

[10]

других

Математический

аппарат

теории

упруго

ползучего

тела

Маслова

Арутюняна

также

не

имел

адекватную

реологическую

модель

Отсутствие

соответствующей

механической

моде

ли

затрудняло

внедрение

этой

теории

динамику

сооружений

для

оценок

упругой

неупру

гой

энергии

деформирования

диссипативных

составляющих

вообще

неотрицательной

ско

рости

рассеивания

энергии

частности

Начиная

момента

приготовления

высокопрочных

бетонах

происходит

непрерыв

ный

процесс

старения

–

возрастом

меняются

модуль

упругости

модуль

сдвига

коэффици

ент

вязкости

чтобы

адекватно

отражать

старение

(

взросление

)

их

реологическую

мо

дель

необходимо

собрать

из

стареющих

со

временем

упругих

вязких

элементов

тем

самым

создавая

вязкоупругие

стареющие

модели

Для

использования

упругой

пружины

модели

вязко

упруго

стареющего

материала

коэффициент

упругости

ставим

зависимость

от

времени

)(tE

Очевидно

что

для

взрос

леющего

бетона

функция

)(tE

должна

быть

возрастающей

удовлетворяющей

условию

0)(

′

Поскольку

активность

процесса

взросления

возрастом

стареющего

бетона

падает

то

)(tE

′

ростом

времени

асимптотически

стремится

нулю

Это

значит

что

вторая

произ

водная

от

функции

)(tE

по

времени

должна

удовлетворять

условию

0)(

′

Таким

усло

виям

удовлетворяет

эмпирическая

формула

)1()(

eaEtE

−

∞

−=

, (2)

где

,, aaE

∞

–

опытные

параметры

Эта

формула

для

взрослеющих

со

временем

упругих

пружин

имеет

простой

удобный

для

применения

аналитических

расчетах

экспоненциальный

вид

Однако

на

наш

взгляд

ее

недостатком

является

то

что

значение

модуля

упругости

данный

момент

наблюдения

связывается

величиной

которую

примет

при

∞

→

∞

Очевидно

что

будет

гораз

до

удобнее

обоснованнее

если

)(

связывать

не

неизвестным

∞

)(

со

зна

чением

начале

рассматриваемого

процесса

Величину

)(

легко

определить

опытным

способом

самом

начале

внешне

силового

воздействия

Поэтому

мы

будем

поль

зоваться

формулой

])1()[()(

)(

111

−−

−+=

ebbEtE

, (3)

которая

имеет

все

достоинства

формулы

(2),

удовлетворяет

вышеуказанным

условиям

сво

бодна

от

вышеотмеченного

недостатка

)(

поддается

непосредственному

определению

самом

начале

рассматриваемого

процесса

, bb

–

для

данных

стареющих

материалов

известные

опытные

константы

Когда

напряжение

постоянно

то

деформация

из

за

роста

модуля

упругости

пружины

будет

изменяться

(

падать

)

)(/)()(

tEt

τσε

Если

деформацию

пружины

фиксировать

на

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

_________________________________________________________________________________________________________________

147

начальном

уровне

сonstt == )()(

τεε

то

опять

же

из

за

изменения

)(

напряжение

будет

меняться

)(/)(/)()()()(

111

ττστεσ

EtEtEt ==

Рост

)(

приводит

тому

что

для

поддержания

постоянной

деформации

требуется

процесс

обратный

релаксации

–

не

спад

напряжения

его

рост

Это

необходимо

учесть

при

анализе

длительных

релаксационных

процессов

выделяя

ту

часть

изменения

напряжения

которая

вызвана

сугубо

изменением

)(

Вызванное

переменным

напряжением

)(

изме

нение

деформации

при

этом

по

принципу

суперпозиции

будет

)(

)()(

)(

),(

tEtE

τστσ

τε

∂

∫

. (4)

Формула

)(/)(),(

tEtt

στε

позволяет

сделать

вывод

рассмотренном

промежутке

времени

−t

какая

бы

не

была

закономерность

изменения

напряжения

модуля

деформа

ции

окончательное

значение

упругой

деформации

однозначно

зависит

от

конечного

значе

ния

)(

Это

значит

что

длительно

накопленная

промежутке

времени

−t

упру

гая

деформация

),(

τε

равняется

упруго

мгновенной

деформации

),(

),(),(

ttt

ετε

≡

целью

применения

элемента

вязкости

стареющей

модели

необходимо

величину

вязкости

ставить

зависимость

от

возраста

Для

этого

возьмем

простую

экспоненциаль

ную

зависимость

изменения

)(

ηη

)( =

, (5)

где

–

коэффициент

вязкости

начальный

момент

при

=0,

. )0(

ηη

Согласно

зависимости

(5),

начиная

возраста

=0,

коэффициент

)(

при

∞

→

∞

→

)(

при

этом

теряя

свою

подвижность

вязкостной

элемент

взросления

выходит

из

строя

переставая

участвовать

процессе

деформации

что

соответствует

полному

старению

(

взрослению

)

материала

Связь

между

напряжением

деформацией

для

взрослеющего

элемента

вязкости

εησ

)(

(6)

При

постоянном

напряжении

)(

τσσ

интегрирование

этого

выражения

пределами

дает

).()(

eet

γγτ

γη

−−

−=

(7)

Очевидно

что

момент

начала

загружения

для

стареющих

моделей

(

как

вязкости

так

упругих

пружин

них

)

является

определяющим

фактором

Мерой

вязкости

здесь

как

следует

из

(7),

является

аналитическая

функция

γητ

γγτ

/)(),(

eetC

−−

−=

. (8)

Как

видно

если

возраст

элемента

момент

загружения

достаточно

велик

то

мера

вязкости

близка

нулю

из

за

чего

поршень

не

может

двигаться

Когда

напряжение

со

временем

изменяется

)(t

то

интегрирование

формулы

вяз

кости

(6)

дает

∫ ∫

−

t t

ded

1 1

.)(

1)(

)(

τ τ

γτ

ττσ

τσ

(9)

Заметим

что

из

(9)

следует

γτ

ητ

−

−=

∂

tC 1),(

. (10)

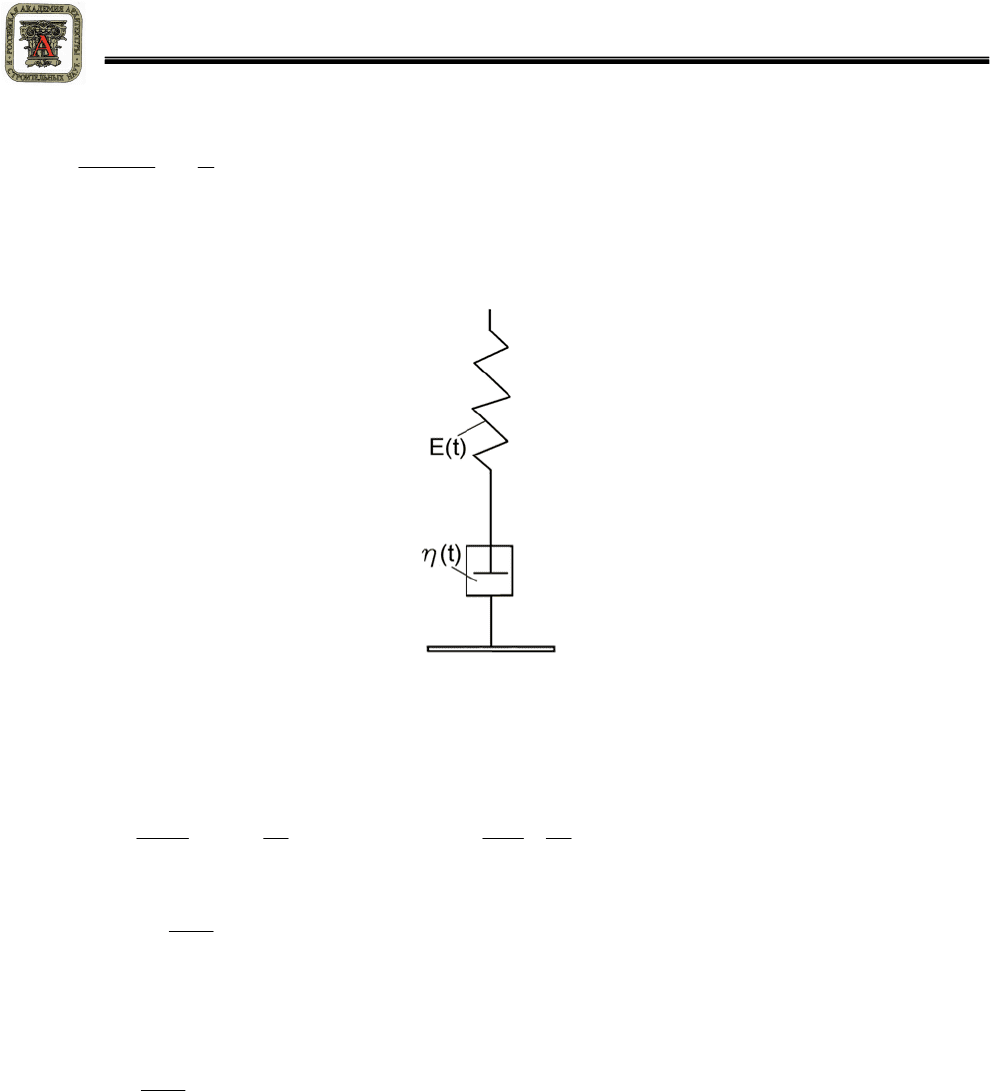
148

____________________________________________

Тогда

учитывая

(10),

(9)

видоизменится

γτ

ητ

−

−=

∂

tC 1),(

Если

рассмотренный

упруго

следовательно

то

получится

модель теории старения

Рисунок

Величиной

общей

деформации модели будет сумма деформаций составляющих м

дель

элементов

)()(

εεε

−

(

)(

γτ

γη

τσ

Величина

удельной

деформации и меры вязкости как следует из

(

)(

),(

γτ

τδ

−

−+=

где

целью

приведения

соответствие с теорией старения бетонов обозначено

Когда

напряжение

со

вр

соотношение

∫

−

)(

γτ

τσγ

Чтобы

уравнение

(14)

представить как интегральное уравнение Вольтерра второго р

да

явном

виде

введе

ядро

вязкости

τσσε

tttE

)()()()(

∫

где

γτ

−

= AetEtK

)(),( .

Сравнивая

ядро

вяз

кости модели вязкоупругого старения с моделью Кельвина зам

чаем

что

влияние

вязкого

элемента в отражается не возрастом

(16),

продолжительностью

силового воздействия

вх

одит

постоянным

коэффициентом упругости

вый

возрастом

модели

параметр Ядро вязкости представляет функционал влияния

ликом

построенный

на

процессе наследственности а аналитическая функция отражает

исключительно

процесс

взросления модели В отрезок времени

нии

вязкого

элемента

игнорируется в то время как построено только на продолжительн

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ И СТРОИТ

МОСКВА

____________________________________________

_____________________________________________________________________

(9)

видоизменится

Если рассмотренный упруго

стареющий

вязко

стареющий

элементы соединить п

следовательно то получится

модель

теории

старения

–

стареющих

бетонов рисунок

Рисунок 1

– Модель теории старения

общей деформации

модели

будет

сумма

деформаций составляющих м

)(

При

постоянном

напряжении













−+=−

−−−

)(

)()

γγτγ

γτ

γη

τσ

Величина удельной деформации

меры

вязкости

как

следует

из

(12)

)(),( );

eeAtCe

γγτγ

−−−

−=

, (13)

где с целью приведения в соответствие

теорией

старения

бетонов

[11]

обозначено

Когда напряжение со

вр

еменем

изменяется

то

учитывая

(9),

получим интегральное

γτ

Чтобы уравнение

(14)

представить

как

интегральное

уравнение

Вольтерра второго р

м ядро

вязкости

),(

ττ

),(

кости

модели

вязкоупругого

старения

моделью Кельвина зам

чаем что влияние вязкого элемента

(1)

отражается

не

возрастом

как это наблюдается в

а продолжительностью

силового

воздействия

−t

Влияние

упругого элемента в

одит постоянным коэффициентом

упругости

то

время

как

(16)

входит как изменч

вый с возрастом модели параметр

Ядро

вязкости

(1)

представляет

функционал влияния

ликом построенный на процессе

наследственности

аналитическая

функция отражает

исключительно процесс взросления

модели

(16)

отрезок

времени

−t

нии вязкого элемента игнорируется

то

время

как

(1)

построено

только

на продолжительн

АРХИТЕКТУРЫ

СТРОИТ

ЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

_____________________________________________________________________

(11)

стареющий элементы

соединить

стареющих бетонов

(

рисунок

1).

общей деформации модели будет сумма деформаций

составляющих

(12)

Величина удельной деформации и меры вязкости как следует из

(12)

, (13)

где с целью приведения в соответствие с теорией старения бетонов

[11]

обозначено

γη

получим

интегральное

(14)

Чтобы уравнение представить как интегральное уравнение

Вольтерра

второго

(15)

(16)

кости модели вязкоупругого старения с моделью

Кельвина

зам

как

это

наблюдается

Влияние упругого

элемента

(1)

в то время как в

(16)

входит

как

изменч

вый с возрастом модели параметр Ядро вязкости представляет функционал

влияния

–

це

ликом построенный на процессе наследственности а аналитическая функция

(16)

отражает

функционирова

нии вязкого элемента игнорируется в то время как построено только

на

продолжительн

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ И СТРОИТ

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

_____________________________________

_______________________________________________

сти

воздействия

усилия

Следовательно было бы корректно ядро вязкости нестареющих вя

оупругих

моделей

представить как

Текущее

время

наблюдения

пределе

∞→t

растет

то

время как по формуле

ному

нулевому

значению

γτ

−

∞=∞ AeEK

)(),(

Характерная

особенность формулы заключается еще и в том что

ле

убывает

экспоненциальной

закономерностью

Этим

отражается

главная реологическая природа

возрастом

их

вязкостные

показатели убывают

Если

εεε

дифференцировать по времени и

)

(

;

εσ

=−=

то

получим

дифференциальное

уравнение деформации модели ВУС

)

(

−+=

Уравнение

(19)

можно

получить и дифференцированием по

шения

(14):

′

−

′

)(

Если

упругостареющей пружиной последовательно соединить не один элемент вя

костарения

элементов

разными коэффициентами вязкости

формация

модели

будет

суммой деформаций составляющих ее элементов

=−=

tttt )()()()(

εεεε

Во

всех

последовательно соединенных элементах действует одинаковое

всех

напр

яжение

если

оно

постоянно то

τσ

−

)(

интегрирование

которого

учетом

(

)(

вi

eet

γτγ

γη

τσ

−−

−=

Тогда

общая

деформация

АРХИТЕКТУРЫ

СТРОИТ

ЕЛЬНЫХ

НАУК

_______________________________________________

_____________________________

сти воздействия усилия Следовательно

было

бы

корректно

ядро

вязкости нестареющих вя

оупругих моделей представить

как

)(

−tK

Текущее время наблюдения

(16)

учитывается

только

через

параметр упругости и в

растет в то время

как

по

формуле

(1)

–

убывает

стремясь к своему предел

Характерная особенность

формулы

(16)

заключается

еще

том

что

ле убывает экспоненциальной

закономерностью

–

ростом

начала

наблю

дения

главная

реологическая

природа

высокопрочных

стареющих бетонов

вязкостные показатели

убывают

дифференцировать

по

времени

учитывая

что

)

то получим дифференциальное

уравнение

деформации

модели

ВУС

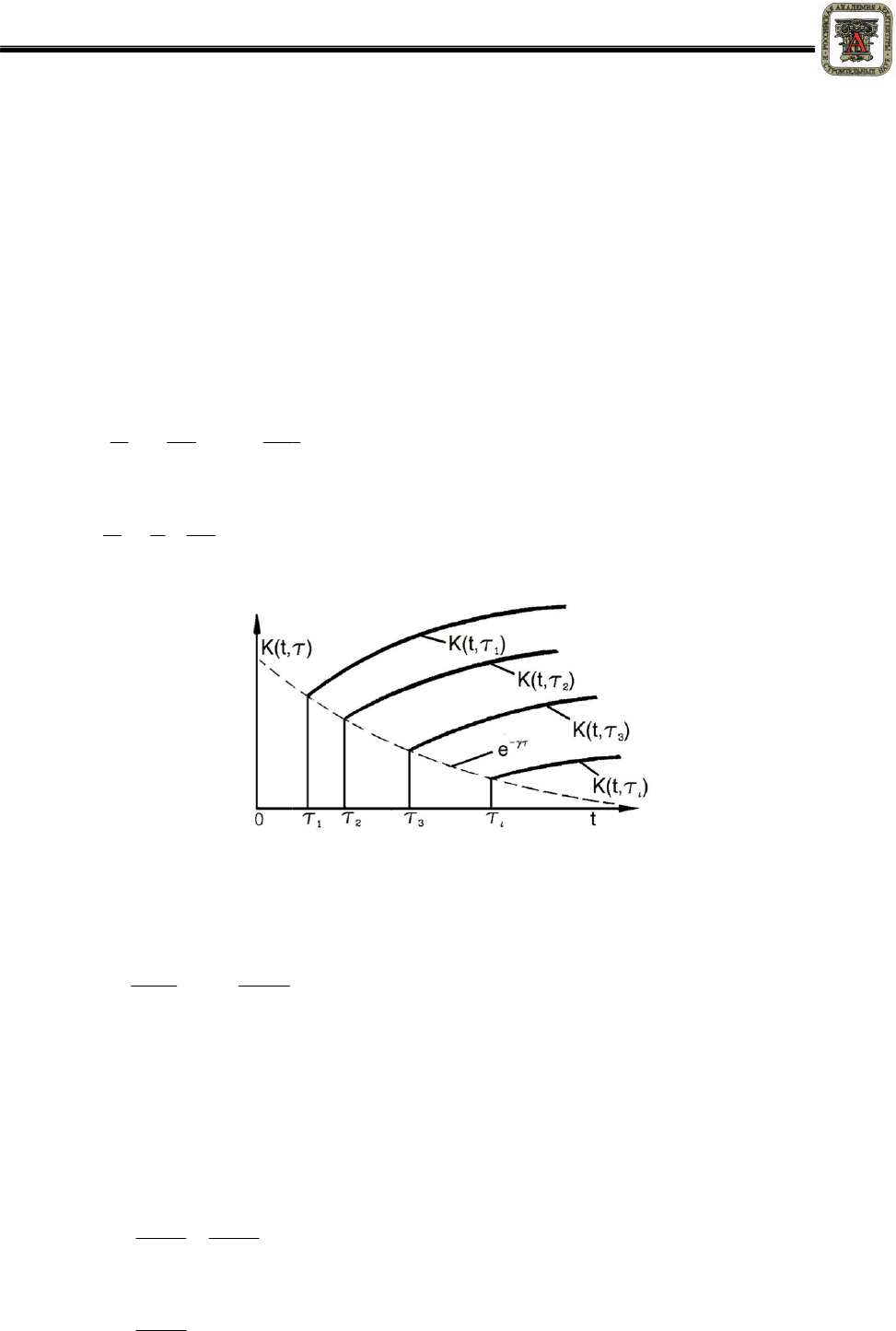
Рисунок – 2

Уравнение можно

получить

дифференцированием

по

интегрального соотн

etA

σγ

−

+ )(

Если с упругостареющей

пружиной

последовательно

соединить

не один элемент вя

элементов с

разными

коэффициентами

вязкости

)(

модели будет суммой

деформаций

составляющих

ее

элементов

∑

+=+++

iym

ttttt

)()()(...)()(

εεεεε

Во всех последовательно

соединенных

элементах

действует

одинаковое

яжение и если оно постоянно

то

интегрирование которого с учетом

0)(

τε

будет

)()()

eeA

γτγ

τσ

−−

−=

Тогда общая деформация

_____________________________

149

сти воздействия усилия Следовательно было бы корректно ядро вязкости

нестареющих

вя

в учитывается только через параметр

упругости

убывает стремясь

своему

предел

(17)

Характерная особенность формулы заключается еще и в том

что

по

этой

форму

дения

(

рисунок

2).

высокопрочных

стареющих

бетонов

–

(18)

(19)

интегрального

соотн

(20)

Если с упругостареющей пружиной последовательно соединить

не

один

элемент

вя

то

общая

де

модели будет суммой деформаций составляющих ее элементов

(21)

Во всех последовательно соединенных элементах действует одинаковое

общее

для

(22)

(23)