Вестник отделения строительных наук РААСН 2011 №15

Подождите немного. Документ загружается.

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

150

_________________________________________________________________________________________________________________













−+=−+=

−−

∑∑

)(

)()()(

)(

iiii

eeA

γτγγτγ

τστσ

τσ

. (24)

Из

(24)

следует

что

мера

вязкости

удельная

деформация

для

такой

модели

будут

)(

),();(),(

iiii

eeA

teeAtC

γτγγτγ

τδτ

−−

−+=−=

∑∑

. (25)

Если

напряжение

модели

)(t

представить

(25),

получим

дифференциальное

уравнение

деформации

модели













−

′

−

′

∑

−

)(

. (26)

интегральное

уравнение

будет

иметь

вид

∫

∑

−

.)(

)(

τγ

τσ

(27)

Для

этой

модели

ядро

вязкости

∑

−

tEtK

.)(),(

τγ

(28)

Так

как

модель

старения

создана

только

на

основе

процесса

взросления

ее

ядро

вяз

кости

убывая

возрастом

модели

становится

незначительным

теряя

ценные

демпферные

свойства

При

расчете

зданий

сооружений

этот

эффект

необходимо

учитывать

особенно

при

динамических

воздействиях

Библиографический список

Тамразян

Реологические

показатели

структурообразования

бетонной

смеси

[

Текст

] /

Тамразян

Бетон

железобетон

, 1998. –

№

Арутюнян

Об

одном

классе

ядер

ползучести

стареющих

материалов

[

Текст

] /

Арутюнян

Зевин

Прикл

мех

, 1982. –

. 18. –

№

4. –

. 14-21.

Малмейстер

Упругость

неупругость

бетона

[

Текст

] /

Малмейстер

Изд

АН

Лат

ССР

, 1957.

Гениев

Метод

определения

динамических

пределов

прочности

бетона

[

Текст

] /

Гениев

Бетон

железобетон

, 1989. –

№

Тамразян

теории

расчета

по

предельным

состояниям

на

основе

реологиче

ской

механики

железобетона

[

Текст

] /

Тамразян

Бетон

железобетон

. – 1999. –

№

Маслов

Термическое

напряженное

состояние

бетонных

массивов

при

учете

ползучести

бетона

[

Текст

] /

Маслов

Известия

НИИГ

Госэнергоиздат

, 1941. –

. 28. –

. 175-188.

Александровский

Расчет

бетонных

железобетонных

конструкций

на

изме

нение

температуры

влажности

учетом

ползучести

[

Текст

] /

Александровский

Стройиздат

, 1973. –

. 432.

Бондаренко

Некоторые

вопросы

нелинейной

теории

железобетона

[

Текст

] /

Бондаренко

. –

Харьков

, 1968. –

. 324.

Галустов

вопросу

нелинейной

теории

ползучести

при

сжатии

[

Текст

] /

Галустов

Гвоздев

Механика

твердого

тела

. – 1972. –

№

1. –

. 85-92.

10.

Карапетян

Ползучесть

весьма

старого

бетона

при

постоянных

ступенчато

возрастающих

нагрузках

[

Текст

] /

Карапетян

Механика

(

НАН

РА

), 1999. –

№

4. –

. 68-74.

11.

Улицкий

Теория

расчет

железобетонных

стержневых

конструкций

уче

том

длительных

процессов

[

Текст

] /

Улицкий

. –

Киев

Будивельник

, 1967. –

. 347.

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

_________________________________________________________________________________________________________________

151

УДК

539.3:624.04

ТРЕЩЕВ

РОМАШИН

(

Тульский

государственный

университет

Тула

)

ОПРЕДЕЛЯЮЩИЕ СООТНОШЕНИЯ ДЛЯ ОРТОТРОПНЫХ

НЕЛИНЕЙНО-УПРУГИХ РАЗНОСОПРОТИВЛЯЮЩИХСЯ

МАТЕРИАЛОВ

Во

многих

отраслях

промышленности

особенно

строительстве

настоящее

время

получили

широкое

применение

конструкционные

материалы

механические

свойства

кото

рых

не

соответствуют

классическим

представлениям

об

упругопластическом

деформирова

нии

твердых

тел

Построение

новой

математической

модели

состояния

конструкционных

материалов

универсально

работающей

при

любых

условиях

нагружения

представляет

собой

одно

из

важнейших

направлений

механики

деформированного

твердого

тела

Требуется

установить

взаимно

однозначные

соотношения

между

компонентами

напряженного

деформированно

го

состояния

указанием

системы

экспериментов

достаточных

для

определения

констант

входящих

уравнения

состояния

характеризующие

механические

свойства

рассматривае

мого

материала

Определяющие

соотношения

для

нелинейно

упругих

структурно

ортотропных

мате

риалов

представим

следующим

образом

[1, 2]:

(1)

где

Функции

определяющих

соотношений

будем

вычислять

по

результатам

простейших

экспериментов

Принимая

нелинейную

зависимость

представим

материальные

функции

зависимости

от

отношения

интенсивности

напряжений

интенсивности

деформаций

помощью

программы

Microcal Origin 6.0 (Microcal Software Inc.)

выводится

зависимость

для

функций

1/[

(

)

], 1/[

(

)

]

(

)

(

)

]

для

каждого

эксперимента

По

лученные

выражения

подставляются

формулы

(1)

для

определения

функций

определяю

щих

соотношений

Рассмотрим

композит

–

углеродное

волокно

–

углерод

AVCO Mod 3a [3, 4].

При

одноосном

растяжении

сжатии

направлении

главной

оси

ортотропии

11 1111 1111 11 11 1122 1122

11 22 22 1133 1133 11 33 33

[ ( ) ( ) ] [ ( ) ( )

( )] [ ( ) ( ) ( )] ;

i i i i

i i

e A B A B

A B

ε ε α σ ε ε

α α σ ε ε α α σ

= + + + ×

× + + + ⋅ +

22 1122 1122 11 22 11 2222

2222 22 22 2233 2233 22 33 33

[ ( ) ( )( )] [ ( )

( ) )] [ ( ) ( ) ( )] ;

i i i

e A B A

B A B

ε ε α α σ ε

ε α σ ε ε α α σ

= + + + +

+ + + ⋅ +

33 1133 1133 11 33 11 2233 2233

22 33 22 3333 3333 33 33

[ ( ) ( )( )] [ ( ) ( )

( )] [ ( ) ( ) ] ;

i i i i

i i

e A B A B

A B

ε ε α α σ ε ε

α α σ ε ε α σ

= + + + + ×

× + + +

12 1212 1212 12 12 1212 12

( ( ) ( ) 2 ) ( ) ;

i i i

e A B C

ε ε α τ ε τ

= + =

23 2323 2323 23 23 2323 23

( ( ) ( ) 2 ) ( ) ;

i i i

e A B C

ε ε α τ ε τ

= + =

31 3131 3131 31 31 3131 31

( ( ) ( ) 2 ) ( ) ,

i i i

e A B C

ε ε α τ ε τ

= + =

2 2 2 2 2 2

11 22 22 33 33 11 12 23 31

2 2

( ) ( ) ( ) 3 / 2( )

3 3

/ , ,

i ij ij

ij ij ij ij i ij ij

S S

ε ε ε ε ε ε ε ε ε ε ε ε

α σ σ σ ε ε ε

⋅

= = − + − + − + + +

= = = ×

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

152

_________________________________________________________________________________________________________________

(2)

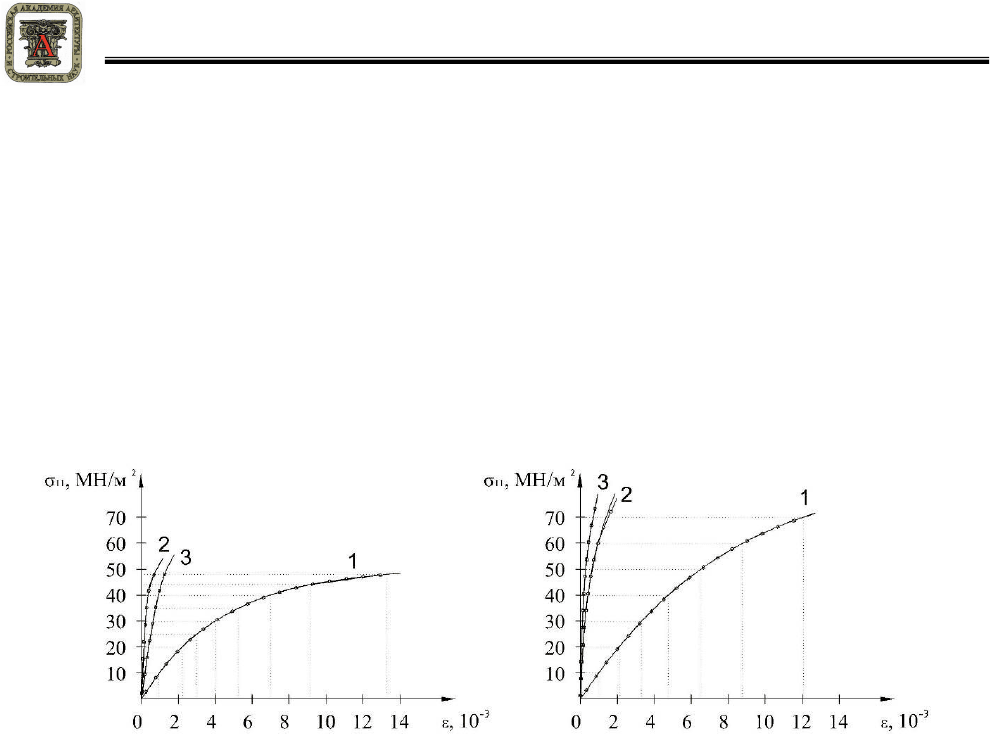
Графическая зависимость напряжений от деформаций при нелинейной аппроксима-

ции для осевых растяжения/сжатия вдоль главной оси анизотропии х

представлена на ри-

сунке 1.

Рисунок 1 – Кривые напряжение-деформация в направлении оси х

: а – растяжение;

б – сжатие; 1 – продольная деформация ε

; 2, 3 – поперечные деформации ε

и ε

;

–––– – экспериментальные данные, ––□–– – нелинейные аппроксимации.

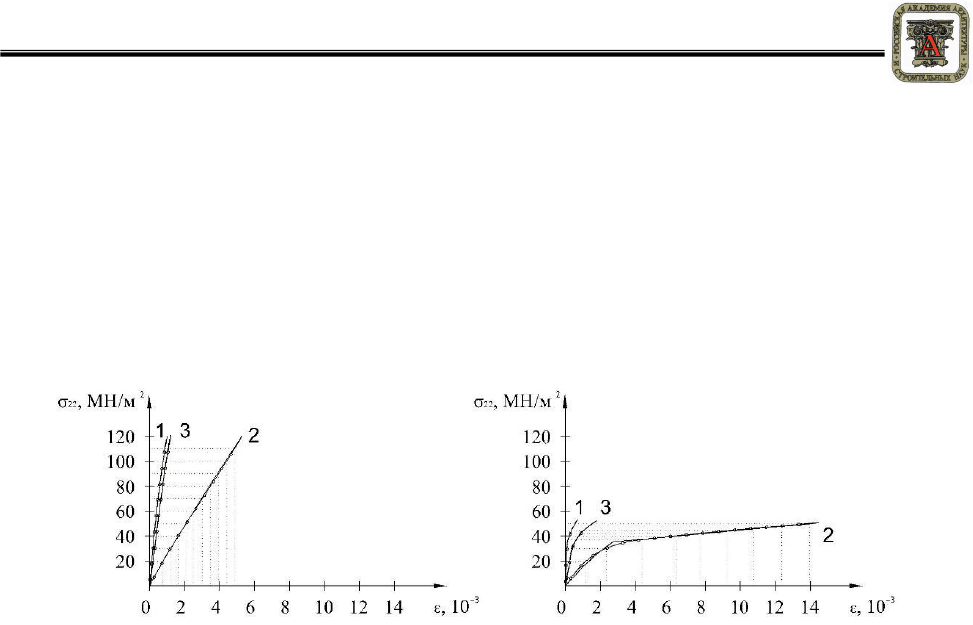
При одноосном растяжении-сжатии в направлении главной оси ортотропии Х

(3)

Графическая зависимость напряжений от деформаций при нелинейной аппроксима-

ции для осевых растяжения/сжатия вдоль главной оси анизотропии х

представлена на ри-

сунке 2. Таким образом, деформации и напряжения достаточно точно связываются зависи-

мостями:

(4)

-4 2 -4 2

1111

-4 2 -4 2

1111

-4 -5 2

1122

( ) 0,5[0,085+0,0146 +5,9 10 (0,094+0,0066 +2,74 10 )];

( ) 0,5[0,006+2,84 10 +6,26 10 (

i i i i i

i i i

ε ε ε ε ε

ε ε ε

= ⋅ ⋅ ⋅ + ⋅ ⋅ ⋅

= ⋅ ⋅ ⋅ − ⋅ ⋅ ⋅

= ⋅ ⋅ ⋅ ⋅ +

-4 -6 2

-4 -5 2 -4 -6 2

1122

-5 2 -5 2

1133

0,0016+8,8 10 +7,2 10 )];

( ) 0,5[0,006+2,84 10 +6,26 10 (0,0016+8,8 10 +7

,2 10 )];

( ) 0,5[0,018+0,0011 -2,54 10 (0,005+0,0013 +6,8 10 )];

(

i i

i i i i i

ε ε

ε ε ε ε ε

⋅ ⋅ ⋅ ⋅

= ⋅ ⋅ ⋅ ⋅ − ⋅ ⋅ ⋅ ⋅

= ⋅ ⋅ ⋅ + ⋅ ⋅ ⋅

-5 2 -5 2

) 0,5[0,018+0,0011 -2,54 10 (0,005+0,0013 +6,8 10 )].

i i i i

ε ε ε ε

= ⋅ ⋅ ⋅ − ⋅ ⋅ ⋅

-4 -5 2 -4 -6 2

2211

-4 -5 2 -4 -6 2

2211

2222

( ) 0,5[0,006+2,9 10 +6,16 10 (0,0016+8,8 10 +7,

25 10 )];

( ) 0,5[0,006+2,9 10 +6,16 10 (0,0016+8,8 10 +7,

25 10 )];

( ) 0,5[0,037+0,0038 -5,1 10

i i i i i

i i

ε ε ε ε ε

ε ε

= ⋅ ⋅ ⋅ ⋅ + ⋅ ⋅ ⋅ ⋅

= ⋅ ⋅ ⋅ ⋅ − ⋅ ⋅ ⋅ ⋅

= ⋅ ⋅

-4 2 -4 2

2222

-4 2 -5 2

2233

(0,03+0,03 -5,4 10 )];

( ) 0,5[0,037+0,0038 -5,1 10 (0,03+0,03 -5,4 10 )];

( ) 0,5[0,011-0,0014 +2,88 10 (0,011+0,0016 +3,74 10 )];

( ) 0,5[0

i i i

i i i i i

ε ε ε

ε ε ε ε ε

⋅ + ⋅ ⋅ ⋅

= ⋅ ⋅ ⋅ − ⋅ ⋅ ⋅

= ⋅ ⋅ ⋅ + ⋅ ⋅ ⋅

-4 2 -5 2

,011-0,0014 +2,88 10 (0,011+0,0016 +3,74 10 )].

i i i i

ε ε ε ε

⋅ ⋅ ⋅ − ⋅ ⋅ ⋅

-4 2 -4 2

11 11

-4 -5 2 -4

[0,5[0,085+0,0146 +5,9 10 (0,094+0,0066 +2,74 10 )]

0,5[0,085+0,0146 +5,9 10 (0,094+0,0066 +2,74 10 )] ]

[0,5[0,006+2,84 10 +6,26 10 (0,0016+8,8 1

i i i i

i i

ε ε ε ε

ε ε ε ε α σ

ε ε

= ⋅ ⋅ ⋅ + ⋅ ⋅ ⋅ +

+ ⋅ ⋅ ⋅ − ⋅ ⋅ ⋅

+ ⋅ ⋅ ⋅ ⋅ + ⋅ ⋅

-6 2

-4 -5 2 -4 -6 2

-5 2

11 22 22

-5 2

+7,2 10 )]

0,5[0,006+2,84 10 +6,26 10 (0,0016+8,8 10 +7,2

10 )]

( )] [0,5[0,018+0,0011 -2,54 10 (0,005+0,0013 +

+6,8 10 )] 0,5[0,018+0,0011 2,54 1

i i

i i i i

i i i

i i

ε ε

ε ε ε ε

α α σ ε ε ε

ε ε

⋅ ⋅ +

+ ⋅ ⋅ ⋅ ⋅ − ⋅ ⋅ ⋅ ⋅ ×

× + + ⋅ ⋅ ⋅ + ⋅

⋅ ⋅ + ⋅ − ⋅

-5 2

11 33 33

0 (0,005+0,0013 +

+6,8 10 )]( )] ;

i i

ε ε

ε α α σ

⋅ − ⋅

⋅ ⋅ +

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

_________________________________________________________________________________________________________________

153

(5)

Рисунок 2 – Кривые напряжение-деформация в направлении оси х

: а – растяжение;

б – сжатие; 2 – продольная деформация ε

; 1, 3 – поперечные деформации ε

и ε

;

–––– – экспериментальные данные, ––□–– – нелинейные аппроксимации

Из анализов проведенных исследований можно утверждать, что нелинейная аппрокси-

мация кривых деформирования дает результаты, максимально приближенные к эксперимен-

там. Поэтому очевидно, что предложенная модель ортотропных нелинейно-упругих разносо-

противляющихся материалов наиболее предпочтительна в случае расчета конструкций, ра-

ботающих при сложных напряженных состояниях.

Библиографический список

1. Амбарцумян, С.А. Общая теория анизотропных оболочек [Текст] / С.А. Амбарцу-

мян. – М.: Наука, 1974. – 446 с.

2. Трещев, А.А. Теория деформирования разносопротивляющихся материалов. Тон-

кие пластины и оболочки [Текст] / А.А. Трещев, Н.М. Матченко. – Москва – Тула: РААСН

ТулГУ, 2005. – 186 с.

3. Jones R.M. Theoretical-experimental correlation of material models for non-linear de-

formation of graphite / R.M. Jones, D.A.R. Nelson // AIAA Journal. – 1976. – Vol. 14. – № 10. –

P. 1427-1435.

4. Jones R.M. Further characteristics of a nonlinear material model for ATJ-S Graphite /

R.M. Jones, D.A.R. Nelson // Journal Composit Materials – 1975. – Vol. 9. – №7. – P. 251-265.

-4 -5 2 -4 -6 2

-4 2

11 22 11

[0,5[0,006+2,84 10 +6,26 10 (0,0016+8,8 1 +7,2 10 )]

0,5[0,006+2,84 10 +6,26 10 (0,0016+8,8 10 +7,2 10 )]

( )] [0,5[0,037+0,0038 -5,1 10 (0

i i i i

i i

ε ε ε ε

α α σ ε ε

= ⋅ ⋅ ⋅ ⋅ + ⋅ ⋅ ⋅ ⋅ +

+ ⋅ ⋅ ⋅ ⋅ − ⋅ ⋅ ⋅ ⋅ ×

× + + ⋅ ⋅ ⋅ +

-4 2

-4 2 -4 2

22 22

-4 2 -5 2

-4

,03+0,03 -5,4 10 )]

0,5[0,037+0,0038 -5,1 10 (0,03+0,03 -5,4 10 )] )] 0,5

[0,011-0,0014 +2,88 10 (0,011+0,0016 +3,74 10 ) 0,5

[0,011-0,0014 +2,88 10

i i

i i i i

i i

ε ε

ε ε ε ε α σ

ε ε ε ε

ε ε

⋅ ⋅ ⋅ +

+ ⋅ ⋅ ⋅ − ⋅ ⋅ ⋅ + ×

× ⋅ ⋅ ⋅ + ⋅ ⋅ ⋅ + ×

× ⋅ ⋅ ⋅

2 -5 2

22 33 33

(0,011+0,0016 +3,74 10 )] ( )] ;

i i

ε ε α α σ

− ⋅ ⋅ ⋅ ⋅ +

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

154

_________________________________________________________________________________________________________________

УДК 624.012.4: 624.042.5:614.841.33

ФЕДОРОВ В.С., ЛЕВИТСКИЙ В.Е., ГРАМИНОВСКИЙ Н.А.

(Московский государственный университет путей сообщения, г. Москва)

АНАЛИЗ ДИАГРАММ «МОМЕНТ-КРИВИЗНА» НЕРАВНОМЕРНО

НАГРЕТОГО ЖЕ ЛЕЗОБЕТОННОГО ЭЛЕМЕНТА, ПОЛУЧЕННЫХ

ИЗ РАСЧЕТА ПО ДЕФОРМАЦИОННОЙ МОДЕЛИ

Традиционные методы расчета железобетонных элементов предполагают раздельное

определение несущей способности по предельным усилиям, а кривизны изогнутой оси – по

сложным полуэмпирическим формулам. Устранение указанного недостатка достигается ис-

пользованием деформационной модели сопротивления нормальных сечений, получившей в

последнее время широкое распространение в научных исследованиях и в новых норматив-

ных документах [1].

Деформационная модель позволяет на единой методологической основе определить

напряженное и деформированное состояние элемента на всех стадиях его работы, что обоб-

щенно отражается в виде диаграммы «момент-кривизна». Расчетное построение такой диа-

граммы дает возможность обоснованно оценить влияние трещинообразования и нелинейных

деформаций (физической нелинейности) железобетона на механизм перераспределения уси-

лий в статически неопределимых системах; проанализировать степень проработки нисходя-

щей ветви диаграммы деформирования бетона при исчерпании несущей способности эле-

мента; выявить отклонения значений несущей способности, найденных с применением де-

формационной модели, и из традиционного расчета по предельным усилиям.

Анализ рассматриваемых в данной работе диаграмм «момент-кривизна» неравномер-

но нагретого железобетонного элемента, полученных из расчета по деформационной модели,

позволяет также оценить развитие температурной кривизны, снижение изгибной жесткости с

ростом температуры, различия в работе элемента при изменении знака момента.

Вначале кратко остановимся на содержании применяемой деформационной модели

сопротивления нормальных сечений. Модель относится к дискретным, то есть для расчета

сечение элемента необходимо разбить на участки, в пределах которых напряжения, дефор-

мации и температура нагрева считаются постоянными. Далее, как и в любой модели сопро-

тивления, следуя В.М. Бондаренко, вполне закономерно выделить три основные составляю-

щие – физическая модель (описание процесса в физически содержательных терминах), рас-

четная модель (исходные предпосылки и упрощающие гипотезы), математическая модель

(разрешающие уравнения).

Не отвлекаясь на описание физической модели, которое достаточно полно представ-

лено в [2], отметим, что расчетная деформационная модель состоит из трех общих для ме-

ханики деформируемого твердого тела групп условий, а математическая модель – соответ-

ственно, из трех групп определяющих соотношений, которые применительно к плоскому из-

гибу в условиях температурного воздействия приобретают следующий вид:

Статические соотношения (уравнения равновесия):

tjsib

tib

AAN

,,,,

∑

σσ

; (1)

jsjs

tjsibib

tib

AyAyM

,,,,,,

∑

σσ

, (2)

где N, M – продольная сила и изгибающий момент от внешней нагрузки; σ

b,ti

, σ

s,tj

– напряже-

ния на элементарных участках бетона и арматуры; A

b,i

, A

s,j

– площади элементарных участ-

ков; y

b,i

, y

s,j

– координаты центров тяжести элементарных участков относительно выбранной

моментной оси.

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

_________________________________________________________________________________________________________________

155

Геометрические соотношения (уравнения совместности деформаций в соответствии с

гипотезой плоских сечений):

ibtt

tem

tibtib

)(

⋅+=+

χεεε

, (3)

jstt

tem

tjstjs

)(

⋅+=+

χεεε

, (4)

где ε

b,ti

, ε

s,tj

)(

tem

tib

)(

tem

tjs

– соответственно силовые и температурные деформации бетона и

арматуры; ε

– обобщенная линейная деформация элемента, выражает удлинение (или укоро-

чение) продольной оси; χ

– обобщенная угловая деформация, выражает кривизну продоль-

ной оси (угол поворота торцевых сечений).

Физические соотношения (уравнения состояния):

b,ti

= ε

b,ti

, (5)

s,tj

= ε

s,tj

, (6)

где E

b,ti

, E

s,tj

– секущие модули деформаций соответственно бетона и арматуры; ν

b,ti

, ν

s,tj

–

коэффициенты секущих модулей (по Н.И. Карпенко) или коэффициенты упругости (по

В.И. Мурашеву); E

b,ti

, E

– начальные модули деформаций бетона (при данной температуре

нагрева) и арматуры.

Для диаграммы деформирования бетона:

])([exp

,,,

tib

titibtib

ην

−=

; (7)

b,ti

= – ln (ν

bu,ti

); (8)

tibu

tib

, (9)

где k

b,ti

– параметр нелинейности диаграммы; η

,ti

– уровень деформаций бетона, равный от-

ношению силовых деформаций ε

b,ti

к их предельной величине при данной температуре ε

bu,ti

;

bu,ti

– предельный коэффициент секущего модуля при данной температуре:

bu,ti

= ε

bu,0

/ β

b,ti

, (10)

bu,ti

= ν

bu,0

⋅ γ

b,ti

, (11)

где ε

bu,0

и ν

bu,0

– соответственно предельные деформации и предельный коэффициент секу-

щего модуля бетона до нагрева; ν

bu,0

= σ

bu,0

/(E

⋅ε

bu,0

); σ

bu,0

и E

– прочность и начальный мо-

дуль деформаций бетона до нагрева; γ

b,ti

и β

b,ti

– коэффициенты снижения соответственно

прочности и начального модуля деформаций бетона при нагреве:

























−

⋅−=

tib

0001

exp

γγ

;

























−

⋅−=

tib

0001

exp

ββ

, (12)

где t

b,i

– температура нагрева бетона, °С; γ, β, m, n –

опытные параметры.

Температурные деформации бетона:





































−

⋅−−⋅=

tem

tib

0001

exp1

)(

αεε

, (13)

где ε

– предельное значение температурных деформаций, к которому они асимптотически

приближаются; α, p – опытные параметры.

В случае растяжения температурная зависимость прочности бетона принимается та-

кой же, как и при сжатии, а исходные характеристики σ

bu,0

и ε

bu,0

заменяются на σ

btu,0

и ε

btu,0

Для диаграммы деформирования арматуры:

в стадии линейно-упругой работы (ε

s,tj

≤ ε

se,tj

) ν

s,tj

= 1;

в стадии нелинейной работы (ε

se,tj

< ε

s,tj

< ε

su,t

tjstjs

tjs

tjse

tjs

)1(

∆∆

+−⋅=

νν

; (14)

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

156

_________________________________________________________________________________________________________________

se,tj

= σ

se,tj

/ E

; (15)

])([exp

,,,

tjs

tjtjstjs

∆

ε∆∆∆

η⋅−=ν

; (16)

tjsetsu

tjsetjs

εε

−

∆

; (17)

∆

s,tj

= – ln (ν

∆

su,tj

); (18)

)(

tjsetsus

tjsetjsu

tjsu

εε

−⋅

−

∆

; (19)

где ν

∆

s,tj

– локальный коэффициент секущего модуля на нелинейном участке, определяется

по аналогии с диаграммой деформирования бетона; η

∆ε

,tj

– уровень приращения деформаций

арматуры по отношению к деформациям предела упругости ε

se,tj

; k

∆

s,tj

– параметр нелинейно-

сти деформирования; ν

∆

su,tj

– предельный локальный коэффициент секущего модуля на нели-

нейном участке диаграммы; σ

se,tj

и σ

su,tj

– соответственно предел упругости и предел текуче-

сти арматуры при данной температуре нагрева:

se,tj

= σ

se,0

⋅ γ

se,tj

; (20)

su,tj

= σ

su,0

⋅ γ

su,tj

, (21)

где σ

se,0

и σ

su,0

– предел упругости и предел текучести арматуры до нагрева; γ

se,tj

и γ

su,tj

– ко-

эффициенты снижения предела упругости и предела текучести при нагреве:

























−

⋅−=

etjse

0001

exp

ωγ

;

























−

⋅−=

utjsu

0001

exp

ωγ

, (22)

где t

s,j

– температура нагрева арматуры, °С; ω

, ω

, c, d – опытные параметры.

В стадии текучести (ε

s,tj

≥ ε

su,t

) диаграмма имеет неограниченный горизонтальный

участок и σ

s,tj

= σ

su,tj

tjss

tjsu

tjs

. (23)

Температурные деформации арматуры определяются при помощи коэффициента тем-

пературного расширения α

s,t

)20(

)(

−⋅=

jsts

tem

tjs

αε

. (24)

При выводе физических соотношений (уравнений связи напряжений и деформаций)

бетона и арматуры при нагреве были приняты следующие исходные предпосылки и упро-

щающие гипотезы:

- нагрев осуществляется по стандартному температурному режиму, принятому для

испытаний конструкций на огнестойкость;

- температурные зависимости механических свойств бетона и арматуры определяются

по результатам нагрева до разрушения нагруженных образцов (при постоянных уровнях на-

гружения);

- деформирование бетона и арматуры условно принимается равновесным на всех ста-

диях работы (не зависящим от времени совместного воздействия температуры и нагрузки);

- деформирование бетона и арматуры условно принимается нелинейно-упругим (де-

формации при нагружении и разгрузке совпадают);

- силовые и температурные деформации материалов развиваются независимо друг от

друга и к ним применим принцип аддитивности (сложения);

- предельные структурные напряжения в бетоне принимаются независящими от темпе-

ратуры нагрева (температурные зависимости для коэффициентов γ

b,ti

и ν

bu,ti

/ν

bu,0

совпадают);

- температурная зависимость прочности бетона принята одинаковой при сжатии и

растяжении;

- взрывообразного разрушения бетона при нагреве не происходит;

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

_________________________________________________________________________________________________________________

157

- максимальные деформации сжатия бетона и растяжения арматуры условно прини-

маются неограниченными, а при растяжении бетона ограничиваются точкой, соответствую-

щей максимальным напряжениям;

- деформации ε

su,t

, соответствующие началу текучести арматуры, приняты не завися-

щими от температуры нагрева;

- температурные деформации арматуры развиваются линейно (коэффициент темпера-

турного расширения α

s,t

принят постоянным);

- модуль упругости арматуры принят не зависящим от температуры нагрева;

- восходящий участок на диаграмме деформирования арматуры, соответствующий ее

упрочнению после достижения предела текучести, не учитывается;

- при выводе математических соотношений для основных параметров, отражающих

состояние материала при изменении температуры и нагрузки, использовано единое кинети-

ческое уравнение нелинейного накопления повреждений при воздействии активного фактора

)(

−

⋅−⋅−=

ау

, (25)

где у, а – соответственно текущее и предельное значения исследуемой характеристики; t –

параметр активного воздействия (температура или деформации); k – параметр затухания

процесса; m – показатель интенсивности.

Решение этого уравнения при граничных условиях a = 0 и y

(t = 0)

= А имеет вид

Aey

−

, на основе которого построены выражения (6), (11), (15) и (21), а при a ≠ 0 и

(t = 0)

= 0 – вид

)1(

eay

−

−⋅=

, на основе которого построено выражение (12).

Не отрицая условности отдельных допущений (в особенности это касается равновес-

ности и нелинейной упругости деформирования), отметим, что результаты расчета огнестой-

кости конструкций по предложенной методике в условиях нагрева по стандартному темпера-

турному режиму удовлетворительно соответствовали опытным данным [2]. Вместе с тем,

принятые предпосылки дают возможность анализировать состояние элемента в любой мо-

мент времени нагрева независимо от его состояния в другие моменты времени.

Решение нелинейной системы (1)-(5) осуществляется методом последовательных при-

ближений, который может быть реализован как в форме метода переменных параметров упру-

гости (последовательно уточняются коэффициенты секущего модуля), так и в форме непо-

средственного подбора значений ε

и χ

, соответствующим условиям равновесия. Результаты,

естественно, должны быть одинаковыми независимо от выбранной формы проведения расчета.

Метод переменных параметров упругости в большинстве случаев позволяет доста-

точно быстро решить конкретную задачу определения кривизны при заданном моменте. Од-

нако на этапах, непосредственно предшествующих исчерпанию несущей способности, ите-

рационный процесс сходится очень медленно, а определять величину несущей способности

по критерию полной потери сходимости итерационного процесса крайне нерационально.

Кроме того, на участках диаграммы «М-χ», где в силу особенностей развития трещин возни-

кают локальные максимумы, метод переменных параметров упругости дает различные ре-

зультаты в зависимости от заданного начального приближения. Указанных недостатков ли-

шен метод непосредственного подбора, где каждому значению кривизны соответствует

только одно значение момента.

Параметры деформированного состояния (кривизны, деформации), найденные в ре-

зультате решения нелинейной системы (1)-(5), справедливы для сечения с трещиной, или для

элемента стержня, у которого сцепление бетона и арматуры обеспечено лишь по торцам, а по

длине отсутствует. В действительности усилия сцепления по длине элемента, сохраняющие-

ся в первые 40…60 мин. нагрева, несколько уменьшают деформации растянутой арматуры и

кривизну элемента. Этот эффект легко учесть традиционным для теории железобетона ко-

эффициентом В.И. Мурашева ψ

s,t

, обеспечивающим переход от деформаций арматуры в се-

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

158

_________________________________________________________________________________________________________________

чении с трещиной к деформациям арматуры в составе железобетонного элемента (к так на-

зываемым средним деформациям). Далее по средним деформациям растянутой арматуры

s,t

и крайнего сжатого волокна бетона ε

b,t1

с применением гипотезы плоских сечений оп-

ределяется кривизна элемента:

1,,,

tbtsts

; (26)

crcs

tts

βψ

⋅−=

, (27)

где σ

s,t

и σ

s,crc

– напряжения в растянутой арматуре соответственно действующие в рассмат-

риваемый момент и действовавшие сразу после образования трещины; β

– коэффициент,

учитывающий неразрывность функции деформаций элемента до и после трещинообразова-

ния, а также снижение сцепления арматуры с бетоном при нагреве:

tsu

crcs

crcsm

⋅













−=

, (28)

где ε

sm,crc

и ε

s,crc

– деформации арматуры непосредственно до и после образования трещины

(резкое приращение деформаций в момент трещинообразования происходит в результате пе-

редачи усилия на арматуру с треснувшего бетона).

В качестве объекта исследований был выбран железобетонный элемент прямоугольно-

го сечения, нагреваемый с одной стороны. Эта схема соответствует работе плит перекрытий.

Исходные данные для расчета приняты следующие: высота сечения плиты 200 мм, ши-

рина 1 м. Армирование двойное (нижнее и верхнее), класс арматуры А400, диаметр 12 мм, шаг

200 мм, расстояние от центра тяжести до ближайшей грани сечения а = а′ = 35 мм. Бетон тя-

желый, на силикатном (гранитном) заполнителе, класс бетона В40.

Предполагая, что расчет проводится на стадии проектирования, используем норма-

тивные сопротивления бетона и арматуры, принятые по СП 52-101-2003 (при эксперимен-

тальных исследованиях для лучшей сходимости с опытными данными следует использовать

средние характеристики): σ

bu,0

= 29,0 МПа; ε

bu,0

= 0,2%; σ

btu,0

= 2,1 МПа; ε

btu,0

= 0,015%; E

36⋅10

МПа; σ

su,0

= 40 МПа; σ

se,0

/ σ

su,0

= 0,975; E

= 200⋅10

МПа. Параметры, характеризую-

щие изменение механических свойств бетона и арматуры при нагреве, приняты по [2]: для

бетона γ = 2,6; β = 3,0; m = 4; n = 0,6; α = 4,4; p = 2,5; ε

= 2,3%; для арматуры ω

= 13,25; ω

12,42; c = 5; d = 3; ε

su,t

= 1,25 %; α

s,t

= 15⋅10

-6

1/°С.

Дискретная расчетная схема сечения представлена в виде набора участков бетона

толщиной 2 мм, расположенных перпендикулярно направлению теплового потока и парал-

лельно моментной оси; арматура задана в виде двух участков – нижнего и верхнего. Мо-

ментная ось принята проходящей на уровне центра тяжести наименее прогретого участка бе-

тона. Температурное поле по сечению определялось по кривым прогрева, представленным в

[1]. Исследуемые моменты времени выбраны с интервалом в 30 мин. При расчете для каждо-

го момента времени задавали ряд значений кривизны, и подбирали соответствующее значе-

ние продольной деформации на уровне моментной оси, при котором выполняется условие

равенства нулю проекций всех сил в сечении на продольную ось элемента (1). Иными слова-

ми, из всех кинематически возможных деформированных состояний выбиралось статически

допустимое. Соответствующий этому состоянию изгибающий момент от внешней нагрузки

определялся из условия (2). В итоге получилась диаграмма, показанная на рисунок 1.

Несущая способность сечения исчерпана, когда кривизна начинает расти без увеличе-

ния нагрузки, то есть в сечении образуется пластический шарнир. Количественное значение

несущей способности – это ордината горизонтального участка на диаграмме. При отсутствии

ограничения максимальных деформаций бетона на нисходящей ветви диаграммы «напряже-

ния-деформации» протяженность горизонтального участка на диаграмме «момент-кривизна»

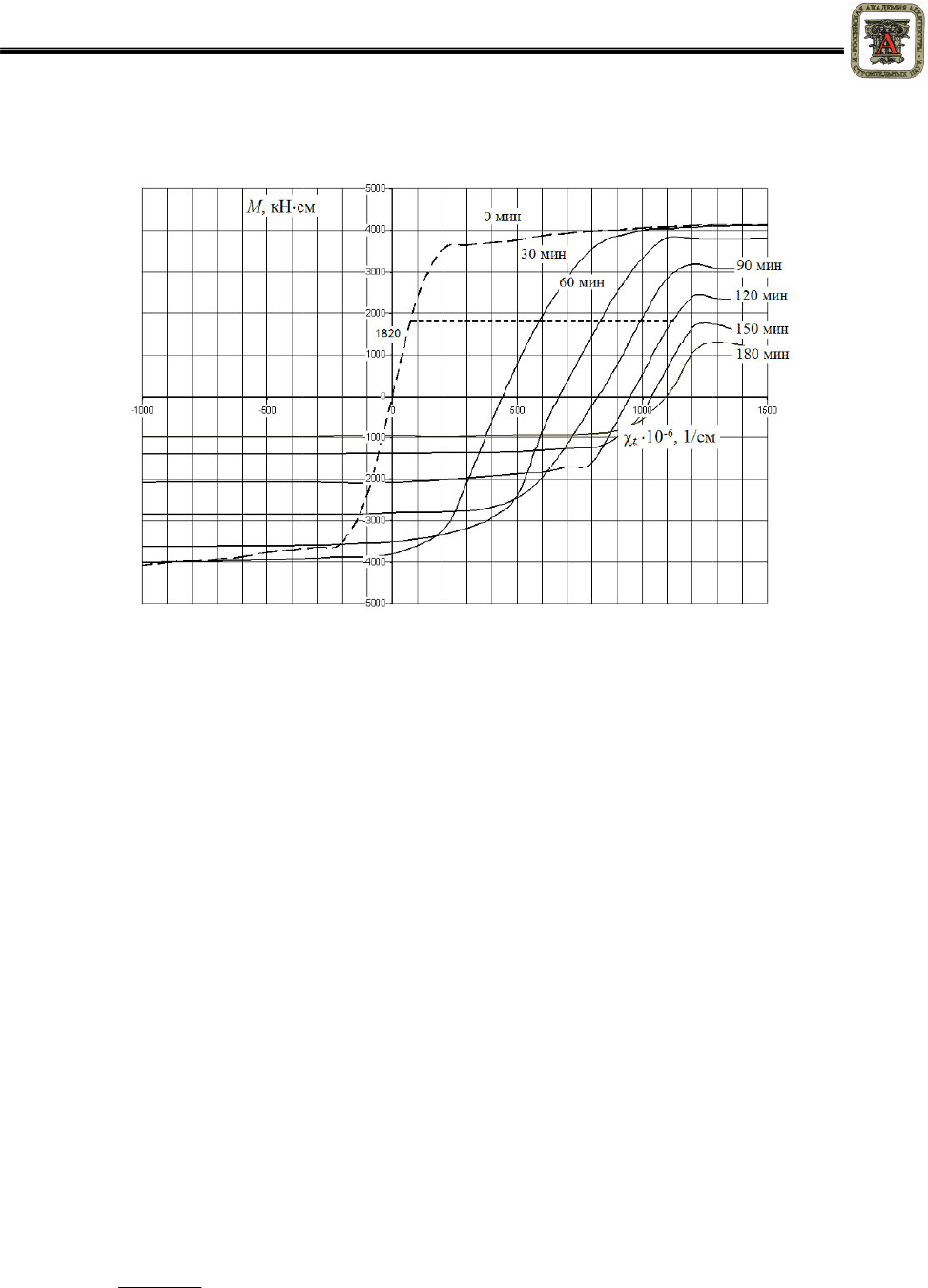
РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ И СТРОИТ

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

_____________________________________

_______________________________________________

получается очень большой.

В конце этого участка происходит снижение момента что связ

но с нарушением внутреннего

силового равновесия в сечении

Рисунок 1 –

Диаграмма момент

Расче

т показал также наличие нескольких локальных максимумов на горизонтальном

участке диаграммы, что связано с особенностями развития трещин перед началом продв

жен

ия трещины несущая способность немного возрастает а после е

затем расте

т вновь). Эти максимумы появляются в связи с принятой предпосылкой о равн

весности деформирования бетона в действительности они не будут наблюдаться поскольку

непрекращающееся развитие деформаций бетона во времени даже при отсутствии роста н

грузки начинается уже после того как напряжения превысили верхнюю параметрическую

точку О.Я. Берга.

Уровни деформаций крайнего волокна сжатого бетона при которых кривизна

ет расти без увеличения нагрузки снижаются по мере прогрева сечения Например при п

ложительном знаке момента максимальный уровень деформаций сжатого бетона в момент

образования пластического шарнира составлял до нагрева примерно через мин

ва он снизился до 0,8, а через 150 мин

лось более значительное снижение до и соответственно Таким образом при нагреве

начало образования пластического шарнира в основном происходит когда сж

работает на восходящей ветви диаграммы напряжения

Как видно из диаграмм «момент

образования пластического шарнира физическая нелинейность деформирования проявляется

не столь сущ

ественно, чтобы вызвать заметное искривление диаграмм не считая стадии

близкие к исчерпанию несущей способности Тангенс угла наклона этих почти линейных

участков диаграмм к оси ординат представляет собой изгибную ж

temt

χχ

−

где М и χ

–

текущее значение момента и соответствующая ему кривизна

ная кривизна, возникающая вследствие неравномерного нагрева и определяемая при

Сохранение параллельности наклонных прямых с течением времени нагрева свид

тельствует о незначительном снижении ж

развит

ия температурной кривизны На рис

АРХИТЕКТУРЫ

СТРОИТ

ЕЛЬНЫХ

НАУК

_______________________________________________

_____________________________

В конце этого участка происходит снижение момента что связ

силового равновесия в сечении.

Диаграмма «момент

кривизна» неравномерно нагретого

железобетонного элемента

т показал также наличие нескольких локальных максимумов на горизонтальном

участке диаграммы что связано с особенностями развития трещин (перед началом продв

ия трещины несущая способность немного возрастает, а после е

образования

т вновь Эти максимумы появляются в связи с принятой предпосылкой о равн

весности деформирования бетона; в действительности они не будут наблюдаться поскольку

непрекращающееся развитие деформаций бетона во времени даже при отсутствии роста н

грузки начинается уже после того, как напряжения превысили верхнюю параметрическую

Уровни деформаций крайнего волокна сжатого бетона, при которых кривизна

ет расти без увеличения нагрузки, снижаются по мере прогрева сечения Например при п

ложительном знаке момента максимальный уровень деформаций сжатого бетона в момент

образования пластического шарнира составлял до нагрева примерно 1,4, через мин

ва он снизился до а через 150 мин

–

до 0,4. При отрицательном знаке момента наблюд

лось более значительное снижение: до 0,4 и 0,2 соответственно. Таким образом при нагреве

начало образования пластического шарнира в основном происходит, когда сж

работает на восходящей ветви диаграммы «напряжения

-деформации».

Как видно из диаграмм «момент

кривизна» в различные моменты времени нагрева до

образования пластического шарнира физическая нелинейность деформирования проявляется

ественно чтобы вызвать заметное искривление диаграмм не считая стадии

близкие к исчерпанию несущей способности). Тангенс угла наклона этих почти линейных

участков диаграмм к оси ординат представляет собой изгибную ж

сткость элемента

текущее значение момента и соответствующая ему кривизна

ная кривизна возникающая вследствие неравномерного нагрева и определяемая при

Сохранение параллельности наклонных прямых с течением времени нагрева свид

тельствует о незначительном снижении ж

есткости, то есть прогиб раст

ия температурной кривизны. На рис

унке

2 показан график развития температурной

_____________________________

159

В конце этого участка происходит снижение момента, что связ

а-

кривизна неравномерно нагретого

т показал также наличие нескольких локальных максимумов на горизонтальном

участке диаграммы что связано с особенностями развития трещин перед началом продв

и-

образования

– падает,

т вновь Эти максимумы появляются в связи с принятой предпосылкой о равн

о-

весности деформирования бетона в действительности они не будут наблюдаться, поскольку

непрекращающееся развитие деформаций бетона во времени даже при отсутствии роста н

а-

грузки начинается уже после того как напряжения превысили верхнюю параметрическую

Уровни деформаций крайнего волокна сжатого бетона при которых кривизна

начина-

ет расти без увеличения нагрузки снижаются по мере прогрева сечения. Например, при п

о-

ложительном знаке момента максимальный уровень деформаций сжатого бетона в момент

образования пластического шарнира составлял до нагрева примерно 1,4, через 90 мин

. нагре-

до При отрицательном знаке момента наблюд

а-

лось более значительное снижение до и соответственно Таким образом, при нагреве

начало образования пластического шарнира в основном происходит когда сж

атый бетон еще

кривизна в различные моменты времени нагрева, до

образования пластического шарнира физическая нелинейность деформирования проявляется

ественно чтобы вызвать заметное искривление диаграмм (не считая стадии,

близкие к исчерпанию несущей способности Тангенс угла наклона этих почти линейных

сткость элемента

(29)

текущее значение момента и соответствующая ему кривизна;

tem

– температур-

ная кривизна возникающая вследствие неравномерного нагрева и определяемая при

М = 0.

Сохранение параллельности наклонных прямых с течением времени нагрева свид

е-

т в основном за счет

показан график развития температурной