Вестник отделения строительных наук РААСН 2011 №15

Подождите немного. Документ загружается.

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

170

_________________________________________________________________________________________________________________

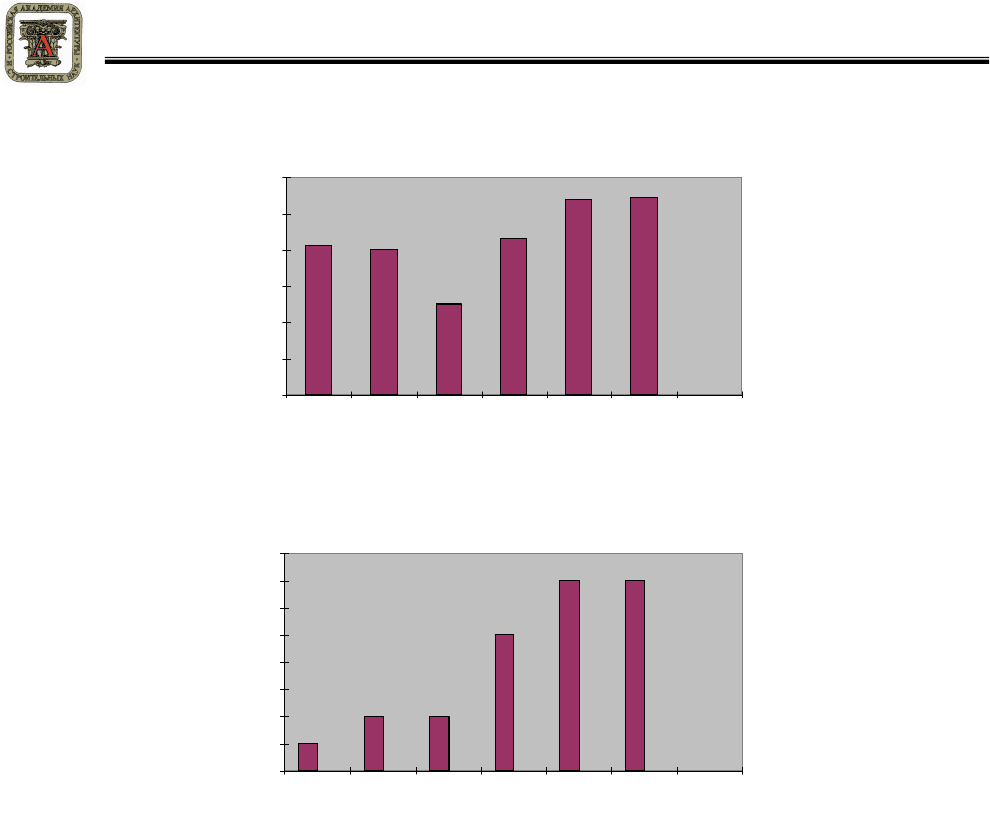
Рисунок 5 – Изменение прочности при сжатии образцов

от содержания МАШ в бетоне

Рисунок 6 – Изменение термической стойкости образцов

от содержания МАШ в бетоне

Разработка и внедрение эффективных, ресурсосберегающих технологий производства

с максимальным использованием местного сырья и техногенных отходов промышленности

является актуальной задачей промышленности строительных материалов.

Библиографический список

1. Деркаченко, Л.И. Минералогия карбида кремния / [Текст] Л.И. Деркаченко. – Л.:

Наука, 1972.

2. Тараканов, О.В. Расширение области применения минеральных шламов в произ-

водстве строительных материалов [Текст] / О.В. Тараканов, Т.В. Пронина // Популярное Бе-

тоноведение, 2006. – №6 . – С. 1-7.

3. Домокеев, А.Г. Строительные материалы [Текст] / А.Г. Домокеев. – М., 1989.

4. Грушко, И.М. Влияние комплексных добавок на прочность бетона [Текст] /

И.М. Грушко, Э.В. Дегтярева // Строительные материалы и конструкции, 1985. – №3. – С. 33-35.

Изменение предела прочности на сжатие от

содержания наполнителей в составе бетона

1 2 3 4 5 6 7

№ состава бе тона

Предел прочности на сжатие, МПа

1 2 3 4 5 6 7

№ состава бе тона

Термическая стойкость

(количество теплосмен)

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

_________________________________________________________________________________________________________________

171

УДК 666.3

АКЧУРИН Т.К., КРУТИЛИН А.А.

(ВолгГАСУ, г. Волгоград)

ПОРИЗАЦИЯ КЕРАМИЧЕСКОЙ МАССЫ НА ОСНОВЕ

ГЛИНИСТОГО СЫРЬЯ ВОЛГОГРАДСКОЙ ОБЛАСТИ

ОТХОДАМИ МЕТАЛЛООБРАБОТКИ

Большим резервом экономии материальных и энергетических ресурсов является ис-

пользование в технологии строительной керамики рядового местного глинистого сырья и во-

влечения в производство техногенных отходов, что позволяет расширить сферу полезного

использования вторичного сырья и снизить себестоимость готовой продукции.

Вопросы использования в технологии строительной керамики местного глинистого сы-

рья и отходов металлообработки при наименьших экономических затратах и сохранении

свойств готовой продукции являются актуальными. Целью исследования является получение

эффективной строительной керамики путем поризации керамической массы отходами металло-

обработки (ОМО) при использовании глинистого сырья Волгоградской области, определение

влияния отходов металлообработки на процессы структурообразования поризованной керамики.

Авторами статьи выдвигается рабочая гипотеза – из глинистого сырья Волгоградской

области при модификации сырьевых шихт железосодержащей выгорающей добавкой метал-

лообработки может быть получена пористая керамика со средней плотностью 600-1000 кг/м

при сохранении технических характеристик готовой продукции.

Месторождения глин Волгоградской области разнообразны и многочисленны (всего

более 50), но разрабатывается их около половины. Глины и суглинки для кирпичного произ-

водства представлены среди четвертичных отложений, покрывающих около трех четвертей

территории Волгоградской области, а также среди неогеновых и юрских отложений. Наи-

большее количество месторождений сосредоточено в пределах г. Волгограда, Урюпинском и

Николаевском районах. Значительные по запасам месторождения сосредоточены в Светло-

ярском и Среднеахтубинском районах.

Химический анализ глинистого сырья проводился в соответствии с требованиями

ГОСТ 2642.3-97÷ГОСТ 2642.5-97 и ГОСТ 2642.7-97 (таблица 1). Химический состав глин

представлен в таблице 1.

Таблица 1 – Химический состав глин месторождений Волгоградской области

Содержание компонентов, масс. %.

SiO

CaO MgO K

O Na

O TiO

п.п.п.

55,61-

72,58

20,36-

10,2

9,80-

3,56

1,08-

4,36

0,76-

1,3

0,58-

0,38

1,75-

2,49

0,56-

0,70

0,08-

0,023

9,81-

5,06

Минералогический состав исследуемых глинистых пород изучался методом рентге-

нофазового анализа (РФА).

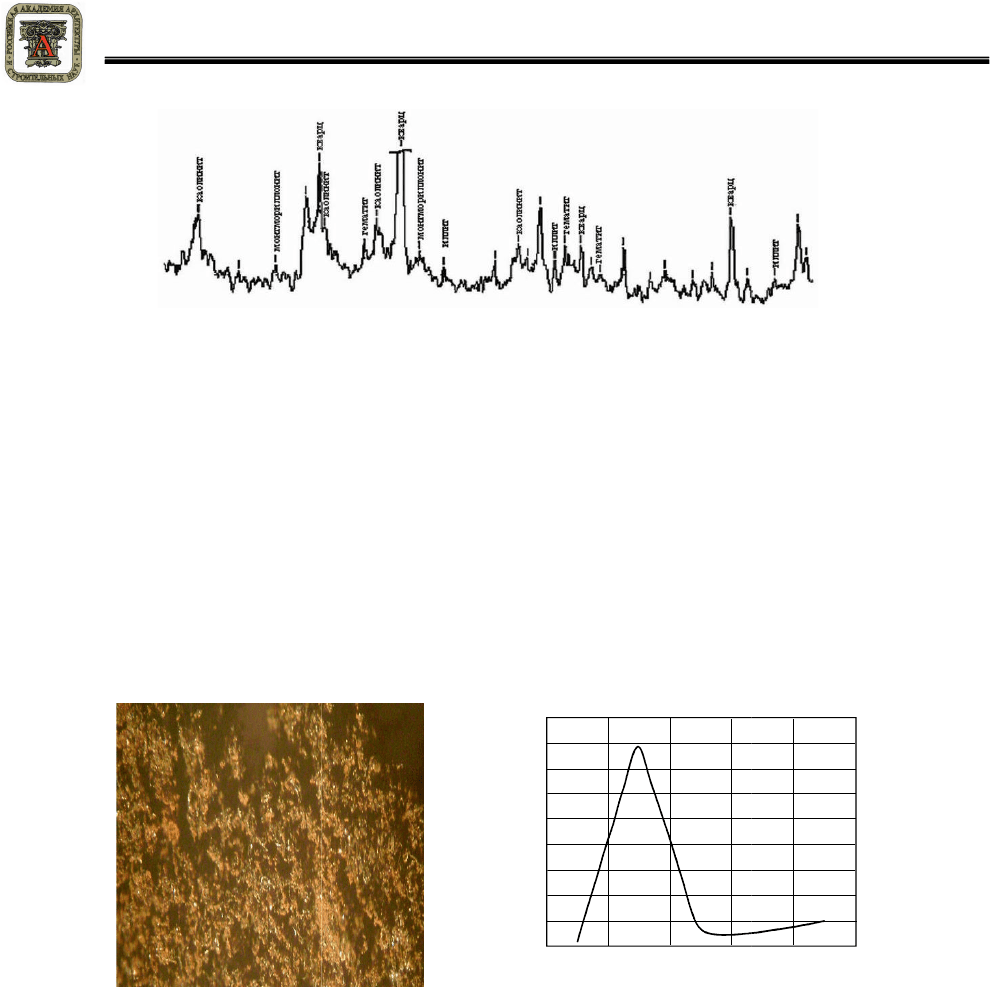
По данным рентгенофазового анализа (рисунок 1) глинистая составляющая средней

пробы глин месторождений Волгоградской области представлена: каолинитом (d/n, Å – 7,225;

4,201; 3,583; 2,567), иллитом (d/n, Å – 3,013; 2,398; 1,723), монтмориллонитом (d/n, Å – 5,011;

3,192), оксиды железа – гематитом (d/n, Å – 3,708; 2,522; 2,214); кремнезем – кварцем (d/n, Å –

4,270; 3,351; 2,2874; 1,822). Выбранный материал глин удовлетворяет основному критерию

пригодности глинистого сырья для производства пористой керамики – способность вспучи-

ваться при термической обработке в пределах 1050-1250°С и образовывать при этом материал,

имеющий ячеистое строение с плотностью в куске в пределах 200-1350 кг/м

172

____________________________________________

Рисунок 1 –

Рентгенофаз

Для модификации глин использована добавка отходов металлообработки ОМО На

металлургических и металлообрабатывающих заводах Волгоградской области скопилось

значительное количество техногенных отходов

ем только на ГПЗ –

15 г. Волжского составлял более тыс т в год

Шлам представляет собой смесь полученную в результате опиловки и шлифования

деталей подшипников качения, обкатки и доводки шаров а также других операций подши

никового произ

водства. Предварительно высушенный до постоянной массы и измельченный

шлам представлен на рисунке 2 (

а)

Рисунок 2 – Шлам: а –

б –

фракционный состав измельченного отхода

По данным химического анализа содержание металла в виде

до 70%, 10

% неметаллических фракций продуктов разрушения абразивного и

при шлифовании) и 20

% смазочно

став шлама предста

влен в таблице Более

представляют собой окисленные металлические и неметаллические частицы сцементир

ванные СОЖ (рисунок 2, а).

Хроматографический анализ отходящих газов при высокотемпературной

шлама показал (хроматограф цвет детектор по теплопроводности детектор ионизации

пламени), что при нагревании до

вергается конверсии водяным паром или кислородом В результате образуется паро

смесь, состоящая из неуглеводородной и углеводородной составляющих а также паров ост

точной влаги (рисунок 3 а, б).

Термодинамический анализ ОМО обосновал возможность практической реализации

процесса газификации углеводородной части ОМО рисунок

материалов. Экспериментально доказано что в газовой фазе присутствуют

, H

, CH

, которые образуются при нагревании ОМО с преобладанием первых трех

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ И СТРОИТ

МОСКВА

____________________________________________

_____________________________________________________________________

Рентгенофаз

овый

анализ средней пробы глин месторождений

Волгоградской области

Для модификации глин использована добавка отходов металлообработки ОМО На

металлургических и металлообрабатывающих заводах Волгоградской области скопилось

значительное количество техногенных отходов

–

шлама металлообработки

г Волжского составлял более 2 тыс. т. в год.

Шлам представляет собой смесь, полученную в результате опиловки и шлифования

деталей подшипников качения, обкатки и доводки шаров, а также других операций подши

водства Предварительно высушенный до постоянной массы и измельченный

шлам представлен на рисунке 2 (

а, б).

б)

измельченный шлам ВПЗ –

15 (увеличение микроскопа х

фракционный состав измельченного отхода

По данным химического анализа содержание металла в виде

окислов железа составляет

неметаллических фракций (продуктов разрушения абразивного и

смазочно

охлаждающей жидкости (СОЖ). Минералогический с

влен в таблице 2. Более 10

-15% объема шлама –

конгломераты которые

представляют собой окисленные металлические и неметаллические частицы сцементир

Хроматографический анализ отходящих газов при высокотемпературной

шлама показал хроматограф цвет 500, детектор по теплопроводности, детектор ионизации

пламени что при нагревании до 800

-900°

С и выше органическая составляющая СОЖ по

вергается конверсии водяным паром или кислородом. В результате образуется паро

смесь состоящая из неуглеводородной и углеводородной составляющих, а также паров ост

Термодинамический анализ ОМО обосновал возможность практической реализации

процесса газификации углеводородной части ОМО (рисунок 3

, б

) при обжиге керамических

материалов Экспериментально доказано, что в газовой фазе присутствуют

которые образуются при нагревании ОМО с преобладанием первых трех

0,02 0,025 0,05 0,75 1,25

Размер отверстий контрольных сит см

Полные остатки на контрольных ситах, %

АРХИТЕКТУРЫ

СТРОИТ

ЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

_____________________________________________________________________

анализ средней пробы глин месторождений

Для модификации глин использована добавка отходов металлообработки (ОМО). На

металлургических и металлообрабатывающих заводах Волгоградской области скопилось

шлама металлообработки,

ежегодный объ-

Шлам представляет собой смесь полученную в результате опиловки и шлифования

деталей подшипников качения обкатки и доводки шаров а также других операций подши

п-

водства Предварительно высушенный до постоянной массы и измельченный

увеличение микроскопа 40х);

окислов железа составляет

неметаллических фракций продуктов разрушения абразивного и

нструмента

охлаждающей жидкости СОЖ Минералогический с

о-

конгломераты, которые

представляют собой окисленные металлические и неметаллические частицы, сцементир

о-

Хроматографический анализ отходящих газов при высокотемпературной

обработке

шлама показал хроматограф цвет детектор по теплопроводности, детектор ионизации

С и выше органическая составляющая СОЖ по

д-

вергается конверсии водяным паром или кислородом В результате образуется паро

газовая

смесь состоящая из неуглеводородной и углеводородной составляющих, а также паров ост

а-

Термодинамический анализ ОМО обосновал возможность практической реализации

при обжиге керамических

материалов Экспериментально доказано что в газовой фазе присутствуют

CO, CO

, H

O, N

которые образуются при нагревании ОМО с преобладанием первых трех.

0,02 0,025 0,05 0,75 1,25

Размер отверстий контрольных сит, см

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ И СТРОИТ

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

_____________________________________

_______________________________________________

Таблица 2 –

Минералогический состав шламов металлообработк

Абразивное зерно (25А,14А минимальная доля С и С

Металлическая стружка

Сколотые абразивные з

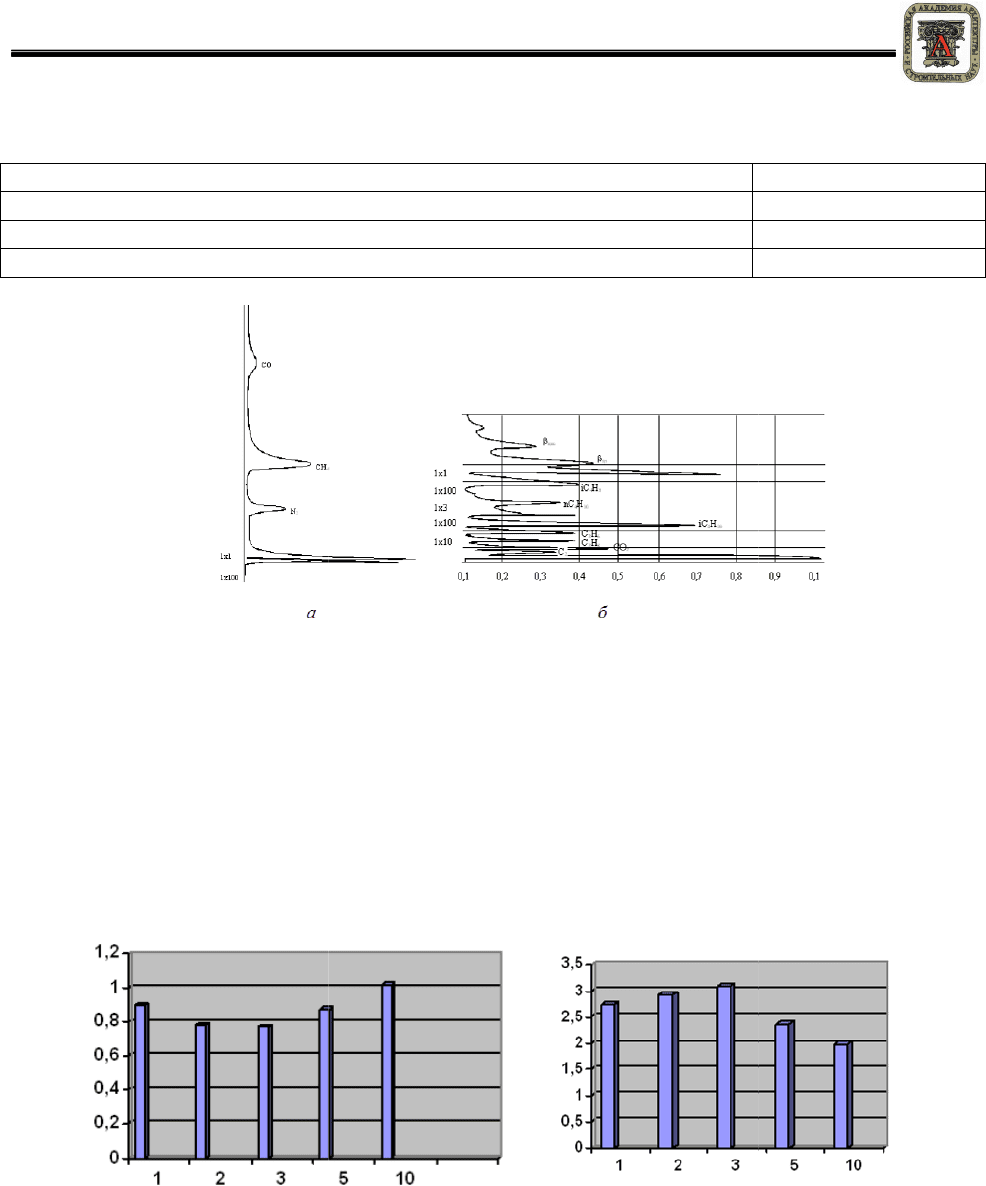
Рисунок 3 –

Неуглеводородная

отходящих

Лабораторные исследования показали что ОМО в исходном состоянии хорошо смеш

вается с замоченной глиной. При этом их содержание в смеси можно доводить до и в

ше. Степень вспучиваемости шихты определялась

объема вспученной массы к объему абсолютно сухого сырца для выбранного материала

глин максимальная величина в шихте составляет

а) б

Рисунок 4 –

Средняя плотность

после обжига в зависимости от содержания шлама в процентах

Как видно из рисунка 4

происходит при добавлении ОМО в количе

зец, в состав которого введен ОМО представлен пористой структурой рисунок Размер

пор колеблется от 100 до 500 мкм имеющих явное вулканическое происхождение на что

указывает форма поры, бо

лее мелкие поры округлой формы

Нау

чной базой получения керамического черепка из предлагаемого глинистого сырья

с добавкой ОМО являются основные положения физической химии законы фазовых пр

вращений в силикатных системах

АРХИТЕКТУРЫ

СТРОИТ

ЕЛЬНЫХ

НАУК

_______________________________________________

_____________________________

Минералогический состав шламов металлообработк

Материал

Абразивное зерно А,14А, минимальная доля 54С и 63С)

Металлическая стружка (

)

Сколотые абразивные з

ерна (обточка)

Неуглеводородная (

а) и углеводородная (а

) составляющ

отходящих

газов

высокотемпературной обработки ОМО

Лабораторные исследования показали, что ОМО в исходном состоянии хорошо смеш

вается с замоченной глиной. При этом их содержание в смеси можно доводить до и в

ше Степень вспучиваемости шихты определялась

коэффициентом, выражающим отношение

объема вспученной массы к объему абсолютно сухого сырца, для выбранного материала

глин максимальная величина в шихте составляет 4.

а) б)

Средняя плотность (

) и коэффициенты вспучивания (

после обжига в зависимости от содержания шлама в процентах

Как видно из рисунка 4

, б

максимальное вспучивание глинисто

происходит при добавлении ОМО в количе

стве 3% по объему от

всей массы Опытный обр

зец в состав которого введен ОМО, представлен пористой структурой (рисунок Размер

пор колеблется от до 500 мкм, имеющих явное «вулканическое» происхождение на что

лее мелкие поры округлой формы.

чной базой получения керамического черепка из предлагаемого глинистого сырья

с добавкой ОМО являются основные положения физической химии, законы фазовых пр

вращений в силикатных системах [1

-3].

_____________________________

173

Содержание, %

составляющ

ие

высокотемпературной обработки ОМО

Лабораторные исследования показали что ОМО в исходном состоянии хорошо смеш

и-

вается с замоченной глиной При этом их содержание в смеси можно доводить до 50% и в

ы-

коэффициентом выражающим отношение

объема вспученной массы к объему абсолютно сухого сырца для выбранного материала

и коэффициенты вспучивания (

б) образцов

после обжига в зависимости от содержания шлама в процентах

максимальное вспучивание глинисто

-шамотной шихты

всей массы. Опытный обр

а-

зец в состав которого введен ОМО представлен пористой структурой (рисунок 5). Размер

пор колеблется от до мкм имеющих явное вулканическое происхождение, на что

чной базой получения керамического черепка из предлагаемого глинистого сырья

с добавкой ОМО являются основные положения физической химии, законы фазовых пр

е-

174

____________________________________________

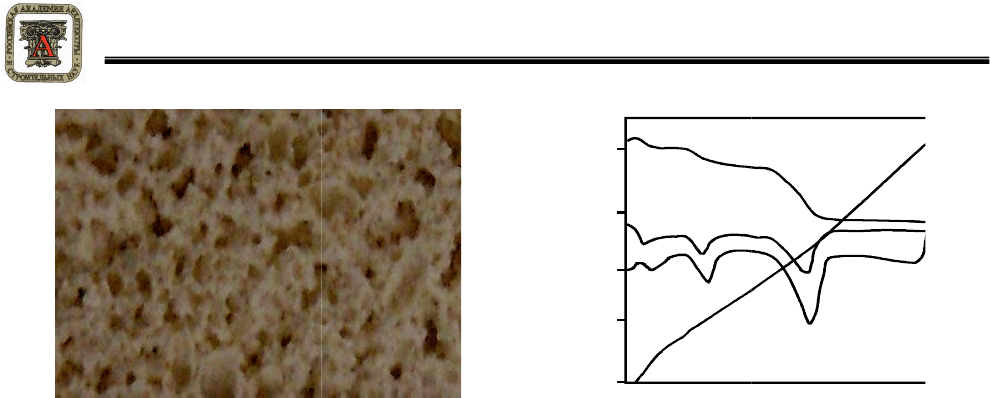
Рисунок 5 – Структура глинисто-

шамотной

с 3%

содержанием добавки

ОМО увеличение х

При высокотемпературном обжиге глинистого сырья с добавкой ОМО содержащего

значительное количество полевошпатных пород и железосодержащих

фицируется процесс спекания керамического черепка за счет образования легкоплавкой э

тектики и растворения в ней других компонентов шихты что способствует жидкофазному

спеканию, образованию новых фаз и получению материала с высокими физ

механическими характеристиками

Источниками газовыделения при спекании керамической шихты являются реакции

разложения и восстановления окислов железа при их взаимодействии с органическими пр

месями ОМО, а также химически связанная вода глинистых минера

тельных реакций пред

ставлена следующими уравнениями

6Fe

→ 4Fe

+ O

; 2

+ С = 2FeO

+ СО;

Влияние этих реа

кций на вспучивание подкрепляет

тельное

количество железистых и органи

керамическую шихту ОМО, состоящую из металлической стружки и СОЖ увеличивает сп

собность глины вспучиваться. Газообразная фаза при вспучивании глин образуется за счет

дегидрата

ции слюдистых минералов которые присутствуют в глинах в качестве примесей и

распадаются с выделением водяных паров Железистым окислам по мнению авторов статьи

отводится не вспомогательная, а приоритетная роль

стых ми

нералов, дегидратацию монтмориллонитовых и гид

Закисное железо интенсифицирует развитие пиропластического состояния глины а о

ганические примеси обусловливают возникновение во

каталитическое действие

на распад слюдистых минералов Восстановительные реакции в

опытных образцах являются источником дополнительного газовыделения в шихте глина

ОМО, не смотря на то, что указанные восстановительные реакции развиваются при температ

рах 750-900°С, что подтвер

ждается дифференциально

ким образом, добавка ОМО в керамическую шихту на основе глин месторождений Волгогра

ской области способствует формированию пористой структуры керамики

1. Будников, П.П. Хи

мическая технология керамики и огнеупоров Текст

Будникова П.

П., Полубояринова Д

Канаев, В.К. Новая технология строительной керамики Текст В К Канаев

Стройиздат, 1990. – 264 с.

3. Таммов, М.

Ч. Моделиро

М.

Ч. Таммов // Строительные материалы

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ И СТРОИТ

МОСКВА

____________________________________________

_____________________________________________________________________

шамотной

керамики

ОМО (увеличение 60х)

Рисунок 6 –

Термограмма

Средне

ахтубинской глины с добавкой

При высокотемпературном обжиге глинистого сырья с добавкой ОМО содержащего

значительное количество полевошпатных пород и железосодержащих

материалов интенс

фицируется процесс спекания керамического черепка за счет образования легкоплавкой э

тектики и растворения в ней других компонентов шихты, что способствует жидкофазному

спеканию образованию новых фаз и получению материала с высокими физ

механическими характеристиками.

Источниками газовыделения при спекании керамической шихты являются реакции

разложения и восстановления окислов железа при их взаимодействии с органическими пр

месями ОМО а также химически связанная вода глинистых минера

лов Схема восстанов

ставлена следующими уравнениями

; 2

→ 6FeO + O

СО;

+ СО = 2FeO + СO

кций на вспучивание подкрепляет

ся тем, что глины содержат знач

количество железистых и органи

ческих примесей, хорошо вспучиваются Добавка в

керамическую шихту ОМО состоящую из металлической стружки и СОЖ увеличивает сп

собность глины вспучиваться. Газообразная фаза при вспучивании глин образуется за счет

ции слюдистых минералов, которые присутствуют в глинах в качестве примесей и

распадаются с выделением водяных паров. Железистым окислам, по мнению авторов статьи

отводится не вспомогательная, а приоритетная роль

–

облегчить и ускорить распад слюд

нералов дегидратацию монтмориллонитовых и гид

рослюдистых минералов

Закисное железо интенсифицирует развитие пиропластического состояния глины а о

ганические примеси обусловливают возникновение во

сстановительной среды оказываю

на распад слюдистых минералов. Восстановительные реакции в

опытных образцах являются источником дополнительного газовыделения в шихте глина

ОМО не смотря на то что указанные восстановительные реакции развиваются при температ

ждается дифференциально

термическим анализом

ким образом добавка ОМО в керамическую шихту на основе глин месторождений Волгогра

ской области способствует формированию пористой структуры керамики.

Библиографический список

мическая технология керамики и огнеупоров Текст

П Полубояринова Д.

Н. – М.: Стройизд, 1972. – 552 с.

Канаев В К Новая технология строительной керамики [Текст] / В К Канаев

Ч Моделиро

вание кинетики вспучивания пористой керамики Текст

Ч Таммов Строительные материалы

, 200. – №10. – С. 25-27.

100100

300

500

700

900

TГ

ДTГ

ДTА

120

310

АРХИТЕКТУРЫ

СТРОИТ

ЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

_____________________________________________________________________

Термограмма

образца

ахтубинской глины с добавкой 3

% ОМО

При высокотемпературном обжиге глинистого сырья с добавкой ОМО, содержащего

материалов, интенс

и-

фицируется процесс спекания керамического черепка за счет образования легкоплавкой э

в-

тектики и растворения в ней других компонентов шихты что способствует жидкофазному

спеканию образованию новых фаз и получению материала с высокими физ

ико-

Источниками газовыделения при спекании керамической шихты являются реакции

разложения и восстановления окислов железа при их взаимодействии с органическими пр

и-

лов. Схема восстанов

и-

ся тем что глины содержат знач

и-

ческих примесей хорошо вспучиваются. Добавка в

керамическую шихту ОМО состоящую из металлической стружки и СОЖ, увеличивает сп

о-

собность глины вспучиваться Газообразная фаза при вспучивании глин образуется за счет

ции слюдистых минералов которые присутствуют в глинах в качестве примесей, и

распадаются с выделением водяных паров Железистым окислам по мнению авторов статьи,

облегчить и ускорить распад слюд

и-

рослюдистых минералов.

Закисное железо интенсифицирует развитие пиропластического состояния глины, а о

р-

сстановительной среды, оказываю

щей

на распад слюдистых минералов Восстановительные реакции в

опытных образцах являются источником дополнительного газовыделения в шихте глина +

ОМО не смотря на то что указанные восстановительные реакции развиваются при температ

у-

термическим анализом

(рисунок 6). Та-

ким образом добавка ОМО в керамическую шихту на основе глин месторождений Волгогра

д-

мическая технология керамики и огнеупоров [Текст] /

Под ред.

Канаев В К Новая технология строительной керамики Текст] / В.К. Канаев,

– М.:

вание кинетики вспучивания пористой керамики [Текст]

ДTА

750

900

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

_________________________________________________________________________________________________________________

175

УДК 691.539.216

БЕЛОВ В.В., СМИРНОВ М.А.

(Тверской государственный технический университет, г. Тверь)

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ МЕТОДИКИ ОПТИМИЗАЦИИ

ГРАНУЛОМЕТРИЧЕСКОГО СОСТАВА КОМПОЗИЦИЙ ДЛЯ

ИЗГОТОВЛЕНИЯ БЕЗОБЖИГОВЫХ СТРОИТЕЛЬНЫХ

КОНГЛОМЕРАТОВ

Существует много предложений по назначению оптимального зернового состава ком-

позиций для изготовления безобжиговых строительных конгломератов, в частности, тяже-

лых бетонов, который должен обеспечивать их минимальную пустотность, определяемую

возможностью плотной укладки зерен материала. По аналогии с плоской задачей при про-

странственном расположении зерен одинакового размера и шарообразной формы за наибо-

лее плотную упаковку без строгого математического обоснования принимают гексагональ-

ную упаковку, для которой характерны 12 контактов у частицы. В то же время отмечается

[1], что до сих пор математически не доказано, что это максимально достижимая плотность.

Из верхних оценок плотности максимальная была найдена в 1958 году К.А. Роджерсом из

Бирмингемского университета; он доказал, что никакая упаковка шаров не может иметь

плотность большую чем ~0,7796. В доказательстве Роджерса не предлагается никакой упа-

ковки шаров, плотность которой была бы близка к найденной оценке. Наиболее плотная упа-

ковка для ограниченного набора фракций шарообразных частиц достигается при плотной

гексагональной упаковке с 4-модальным распределением зерен с размерами D, (√2-1)D,

((√6/2)-1)D, ((2√3/3)-1)D в количественном соотношении 1:1:1:1. При этом пустотность со-

ставит 0,188 или 18,8%. При этом также следует считать, что с точки зрения статики гекса-

гональная упаковка частиц крайне неустойчива, и технологическая ее реализация крайне за-

труднена. Более устойчивой является гексагонально-призматическая упаковка частиц, и наи-

более вероятными и технологически осуществимыми являются многомодальные кубическая

или гексагонально-призматическая упаковки [2].

Показано, что заметное снижение пустотности происходит при переходе от 1-

модальной к 2-модальной упаковке, а дальнейшее увеличение модальности не приводит к

ощутимому результату. Пустотность при плотной кубической упаковке с 2-модальным рас-

пределением зерен по размерам составляет 27,06% в количественном соотношении 1 : 1 и

21,84% – при плотной гексагонально-призматической упаковке с 2-модальным распределе-

нием зерен по размерам в количественном соотношении 1 : 2. Эти данные объясняют акту-

альность современного опыта широкого применения различных микронаполнителей, в част-

ности, в цементных бетонах. Эффект упрочнения вяжущего наполнителем существует при

определенных соотношениях размеров частиц цемента и наполнителя, и частицы последнего

надо также учитывать в общем гранулометрическом составе минеральной части бетона [3].

Если зерна смешиваемых фракций не очень отличаются размером (в заполнителе с

непрерывной гранулометрией), то в случае отклонения его зернового состава от так назы-

ваемой «идеальной» кривой просеивания размер и количество мелких зерен могут оказаться

меньше или больше, чем размер и объем пустот между крупными зернами. В первом случае

мелкие зерна не заполнят полностью объем пустот между крупными зернами, и останется

дополнительная остаточная пористость. Во втором случае мелкие зерна, не умещаясь в пус-

тотах, несколько раздвинут крупный заполнитель. В результате пустотность всей системы

может не только уменьшиться, но даже увеличиться. Такое явление может иметь место при

заполнителе с непрерывной гранулометрией, даже в случае ее соответствия «идеальной»

кривой просеивания, поскольку мелкие зерна в процессе перемешивания и, особенно, при

уплотнении не всегда способны занять свои выгодные позиции. Поэтому считается, что для

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

176

_________________________________________________________________________________________________________________

заполнителя с прерывистой гранулометрией легче реализуется принцип наиболее плотной

упаковки зерен. Причем для этого необходимо, чтобы средний размер зерен каждой фракции

был как минимум в 6,5 раза меньше среднего размера зерен соседней большей фракции.

Тем не менее, многие исследователи считают более эффективным непрерывный зерно-

вой состав заполнителей, так как хотя смеси с прерывистым составом при исключении фрак-

ций средних размеров и обеспечивают меньшую пустотность смеси, однако, в них подвиж-

ность мелких зерен, защемленных между крупными, ограничена и для получения определен-

ной подвижности бетонной смеси толщина обмазки зерен цементным тестом должна быть

больше, чем в смесях с непрерывным зерновым составом, причем это происходит в условиях,

когда возрастает объем мелкой фракции, а, следовательно, и удельная поверхность заполните-

ля. В результате увеличивается расход цемента на обмазку зерен и уменьшается возможность

экономии цемента за счет уменьшения пустотности заполнителя. Кроме того, смеси с преры-

вистым зерновым составом склонны к расслоению, что отрицательно сказывается на однород-

ности бетона. Особенное значение непрерывная оптимальная гранулометрия смеси заполните-

лей приобретает при получении современных самоуплотняющихся высокопрочных бетонов.

В экспериментах по проверке моделей упаковки зернистых сыпучих систем с непре-

рывной гранулометрией [4] находили зависимости насыпной плотности при свободной за-

сыпке и засыпке в условиях встряхивания для многофракционных смесей кварцевого песка.

Сравнение результатов эксперимента и расчетов оптимального состава сыпучей системы по

известным моделям упаковки показало, что наибольшее приближение к экспериментальному

оптимальному зерновому составу из критерия максимальной насыпной плотности по резуль-

татам планированного эксперимента получено по расчетам на основе формулы Фун-

ка/Дингера с коэффициентом распределения n, равным 0,5:

minmax

min

пр

100

−

где

пр

– проход частиц, %, через сито размером Х, мм;

max

– наибольшая крупность зерна

в смеси, мм;

min

– наименьшая крупность зерна в смеси, мм.

По результатам выполненных экспериментов [4] можно сделать вывод, что уравнения

оптимальных кривых просеивания дают только приблизительный состав максимальной упа-

ковки зерен заполнителя, что можно объяснить различной формой зерен реальной сыпучей

системы. Указанные уравнения описывают «идеальную» кривую просеивания для систем с

шарообразной формой зерен и не учитывают возможных отклонений от этой формы для ре-

альных систем. Считается, что учет данного фактора может быть выполнен с помощью ко-

эффициента формы зерна, который определяется как отношение площади поверхности шара

шар

к площади поверхности зерна Ф

равного объема [5]. Коэффициент формы шара равен

единице. При этом, чем сильнее форма зерен отличается от идеальной сферической формы,

тем большую долю в зерновом составе должна занимать меньшая фракция [5]. Тогда уравне-

ние, описывающее «идеальную» кривую просеивания по Фуллеру с учетом коэффициента

формы зерен, может выглядеть следующим образом [6]:

[

]

,100)/)(1(

maxпр

⋅−+=

αα

где

1 К−=α

(коэффициент α для реальных частиц сыпучих систем по данным многих ис-

следователей может изменяться в пределах от 0,08 до 0,14.

Однако кривые просеивания, построенные по уравнению Фуллеру с учетом коэффици-

ента формы, показывают еще большее расхождение с результатами экспериментов. Расчет-

ные методики можно приблизить к реальным условиям и сделать более точными путем вве-

дения коэффициентов формы зерен в уравнение Функа/Дингера, учитывающее как макси-

мальный, так и минимальный размеры зерен.

Экспериментальная проверка моделей упаковки реальных дисперсных систем, наряду с

теоретическим анализом и обобщением, позволила в данной работе предложить усовершенст-

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

_________________________________________________________________________________________________________________

177

вованную формулу «идеальной» или эталонной кривой просеивания, полученную на основе

формулы Функа/Дингера с учетом коэффициента формы частиц. Эта формула имеет вид:

5,0

min

5,0

max

5,0

min

5,0

)1(

100

DХ

пр

−

α−+α=

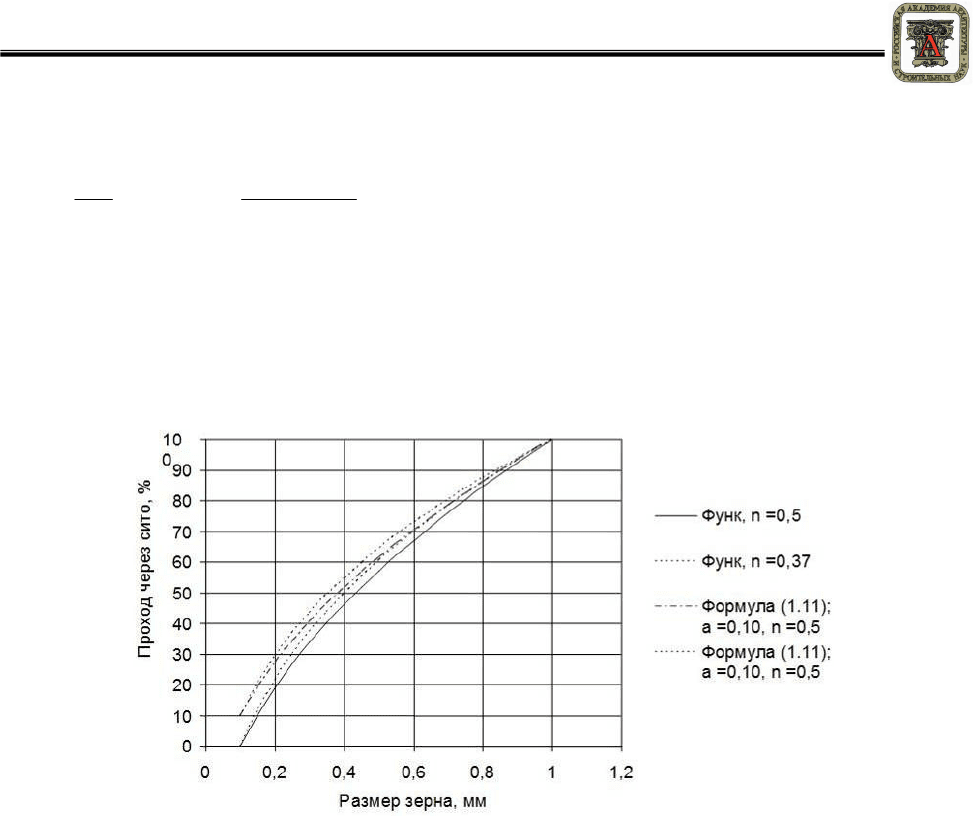
На рисунке 1 показаны графики зависимостей эталонных кривых просеивания, по-

строенные как по уравнению Функа/Дингера при двух значениях коэффициента распределе-

ния (0,5 и 0,37), так и по предлагаемому уравнению также при этих двух значениях коэффи-

циента распределения. Видно, что коэффициент п оказывает влияние в основном на содер-

жание средних фракций, и на основании экспериментов можно утверждать, что более точные

результаты получаются при использовании этого коэффициента, равного 0,5.

Рисунок 1 – Сравнение расчетов оптимального состава сыпучей системы

по известным моделям упаковки и предложенным в работе

Кроме того, для оптимизации упаковок минеральных частиц сырьевых композиций

может быть использована компьютерная программа для моделирования случайных упаковок,

дающая количественную оценку параметров полученной упаковки [7]. В данной программе

использован алгоритм перекатывающихся частиц, который относится к типу “drop and roll”

[8]. С помощью разработанной программы, задавая начальные параметры, можно получить

количественную оценку упакованного массива сферических частиц. Таким образом, про-

грамма позволяет исследовать процесс упаковки двухфракционной системы частиц, с воз-

можностью задания их размеров, количества в пределах своей фракции, а также параметров

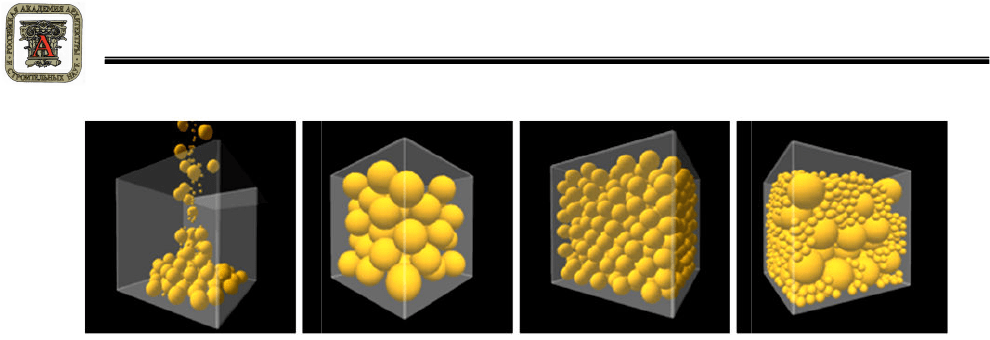
уплотнения, что позволяет добиться более плотных структур. После установки начальных

параметров в режиме построения трехмерной модели можно регулировать процесс заполне-

ния бункера частицами, задавая очередность засыпки фракций, а также включая и отключая

уплотнение (рисунок 2).

Результатом работы программы являются построенная трехмерная модель упаковки

частиц, рассчитанный объем засыпанных частиц, а также пустотность. Использование алго-

ритма, описанного выше, оказывается недостаточно для реконструкции пространственных

свойств материалов, поскольку истинная форма частиц отличается от идеальной (сфериче-

ской). Однако данная идеализированная модель в первом приближении дает количественную

оценку полученной упаковки. Возможность регулирования параметров модели способствует

получению различных типов упаковок, что в свою очередь демонстрирует влияние подбора

состава на структуру композита.

178

____________________________________________

Рисунок

варьирования параметров построения модели

Высоким потенциалом в области усовершенствования составов строительных кон

ломератов обладает комбинированное применение вяжущего и тонкодисперсного наполн

теля. Добавки-

наполнители тонкой например зола

ка, базальтовая мука) и сверхтонкой дисперсности например микрокремнезем позволяют

значительно увеличить плотность упаковки и прочность материалов При этом важне

ше

й задачей является установление границ применимости известных моделей упаковки с

пучих дисперсных

систем по отношению к минимальному критическому размеру зерна

минерального материала, ниже которого происходит изменение баланса поверхностных сил

к действи

ю сил гравитации и следует ожидать принципиальной невозможности плотной

упаковки частиц вследствие образования арочных и мостиковых структур Результаты

экспериментов [10] показали, что при постепенном увеличении содержания тонкодиспер

ной части насыпн

ая плотность бинарной системы резко увеличивается достигая максимал

ного значе

ния при ее содержании

тремум насыпной плотности свидетельствует о достижении состояния когда тонкодиспер

ные частицы располагаю

тся между грубодисперсными не раздвигая их При дальнейшем

увеличении тонкодисперсной части происходит уменьшение насыпной плотности системы

следовательно, в системе начинается явление раздвижки т е частицы меньших размеров

вклиниваются в промежутки ме

которое расстояние. Таким образом на нисходящей части кривых объем тонкодисперсной

части превышает объем межзерновых пустот грубодисперсной части Показано что наиб

лее плотная упаковка частиц в пол

чающихся от расчетных по известным методикам соотношениях тонкой и грубой фракций

что объясняется участием поверхностных сил в законах упаковки полидисперсных систем

При этом возникают новые системы гло

окружены оболочками из частиц мелких фракций за счет проявления поверхностных сил на

межфазной границе раздела грубо

частиц вяжущего вещества на поверхность

глобулированием [11], является полезным и ведущим к повышению плотности и прочности

контактных зон и композита в целом и этот процесс надо усиливать в том числе за счет в

бора оптимальной влажности сырьевой сме

Представленные основы разрабатываемой методики определения оптимальной гран

лометрии полидисперсных систем позволяют обосновать научные предпосылки проектир

вания оптимальных составов строительных смесей

Слоэн, Н.Дж.А. Упаковка шаров

American. Издание на русском языке

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ И СТРОИТ

МОСКВА

____________________________________________

_____________________________________________________________________

– Различные типы

упаковок, полученные вследствие

варьирования параметров построения модели

Высоким потенциалом в области усовершенствования составов строительных кон

ломератов обладает комбинированное применение вяжущего и тонкодисперсного наполн

наполнители тонкой (например, зола

унос, кварцевая мука известняковая м

ка базальтовая мука и сверхтонкой дисперсности (например, микрокремнезем позволяют

значительно увеличить плотность упаковки и прочность материалов [9]. При этом важне

й задачей является установление границ применимости известных моделей упаковки с

систем по отношению к минимальному (критическому размеру зерна

минерального материала ниже которого происходит изменение баланса поверхностных сил

ю сил гравитации и следует ожидать принципиальной невозможности плотной

упаковки частиц вследствие образования «арочных» и «мостиковых» структур Результаты

экспериментов показали, что при постепенном увеличении содержания тонкодиспер

ая плотность бинарной системы резко увеличивается, достигая максимал

ния при ее содержании 5…25

%, а затем вновь уменьшается. Наблюдаемый эк

тремум насыпной плотности свидетельствует о достижении состояния, когда тонкодиспер

тся между грубодисперсными, не раздвигая их При дальнейшем

увеличении тонкодисперсной части происходит уменьшение насыпной плотности системы

следовательно в системе начинается явление раздвижки, т.е. частицы меньших размеров

вклиниваются в промежутки ме

жду крупными частицами, отодвигая их друг от друга на н

которое расстояние Таким образом, на нисходящей части кривых объем тонкодисперсной

части превышает объем межзерновых пустот грубодисперсной части. Показано что наиб

лее плотная упаковка частиц в пол

идисперсной системе достигается при значительно отл

чающихся от расчетных по известным методикам соотношениях тонкой и грубой фракций

что объясняется участием поверхностных сил в законах упаковки полидисперсных систем

При этом возникают новые системы гло

булярного типа, в которых зерна крупной фракции

окружены оболочками из частиц мелких фракций за счет проявления поверхностных сил на

межфазной границе раздела грубо

и тонкодисперсной частей. Процесс налипания мелких

частиц вяжущего вещества на поверхность

крупных частиц заполнителя названный нами

глобулированием является полезным и ведущим к повышению плотности и прочности

контактных зон и композита в целом, и этот процесс надо усиливать, в том числе за счет в

бора оптимальной влажности сырьевой сме

си [12].

Представленные основы разрабатываемой методики определения оптимальной гран

лометрии полидисперсных систем позволяют обосновать научные предпосылки проектир

вания оптимальных составов строительных смесей.

Библиографический список

Слоэн Н Дж А Упаковка шаров

[Текст] / Н.Дж.А. Слоэн

// В мире науки

Издание на русском языке, 1984.

– №3. – С. 72-82.

АРХИТЕКТУРЫ

СТРОИТ

ЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

_____________________________________________________________________

упаковок полученные вследствие

Высоким потенциалом в области усовершенствования составов строительных кон

г-

ломератов обладает комбинированное применение вяжущего и тонкодисперсного наполн

и-

унос кварцевая мука, известняковая м

у-

ка базальтовая мука и сверхтонкой дисперсности например микрокремнезем) позволяют

значительно увеличить плотность упаковки и прочность материалов [9]. При этом важне

й-

й задачей является установление границ применимости известных моделей упаковки с

ы-

систем по отношению к минимальному критическому) размеру зерна

минерального материала ниже которого происходит изменение баланса поверхностных сил

ю сил гравитации и следует ожидать принципиальной невозможности плотной

упаковки частиц вследствие образования арочных и мостиковых» структур. Результаты

экспериментов показали что при постепенном увеличении содержания тонкодиспер

с-

ая плотность бинарной системы резко увеличивается, достигая максимал

ь-

а затем вновь уменьшается. Наблюдаемый эк

с-

тремум насыпной плотности свидетельствует о достижении состояния, когда тонкодиспер

с-

тся между грубодисперсными не раздвигая их. При дальнейшем

увеличении тонкодисперсной части происходит уменьшение насыпной плотности системы,

следовательно в системе начинается явление раздвижки т е частицы меньших размеров

жду крупными частицами отодвигая их друг от друга на н

е-

которое расстояние Таким образом на нисходящей части кривых объем тонкодисперсной

части превышает объем межзерновых пустот грубодисперсной части. Показано, что наиб

о-

идисперсной системе достигается при значительно отл

и-

чающихся от расчетных по известным методикам соотношениях тонкой и грубой фракций,

что объясняется участием поверхностных сил в законах упаковки полидисперсных систем.

булярного типа в которых зерна крупной фракции

окружены оболочками из частиц мелких фракций за счет проявления поверхностных сил на

и тонкодисперсной частей Процесс налипания мелких

крупных частиц заполнителя, названный нами

глобулированием является полезным и ведущим к повышению плотности и прочности

контактных зон и композита в целом и этот процесс надо усиливать в том числе за счет в

ы-

Представленные основы разрабатываемой методики определения оптимальной гран

у-

лометрии полидисперсных систем позволяют обосновать научные предпосылки проектир

о-

В мире науки: Scientific

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

_________________________________________________________________________________________________________________

179

2. Мамыркулов, М.И. Математическое моделирование структуры пористых материа-

лов [Текст] / М.И. Мамыркулов, Ю.А. Мамонтов, К.М. Абдугаппаров, А. Дауренбаев // По-

пулярное бетоноведение, 2008. – №4. – С. 77-78.

3. Хархардин, А.Н. Краевые задачи строительного материаловедения. Часть I. Об оп-

тимальной толщине цементной оболочки на зернах заполнителя в строительных композитах

[Текст] / А.Н. Хархардин // Изв. вузов. Строительство, 2006. – №5. – С. 24-30.

4. Белов, В.В. Оптимизация гранулометрического состава композиций для изготовле-

ния безобжиговых строительных конгломератов [Текст] / В.В. Белов, М.А. Смирнов // Вест-

ник Центрального регионального отделения РААСН. – Воронеж: РААСН, ВГАСУ, 2010. –

Вып. 9. – С. 65-72.

5. Удодов, С.А. Применение пористого заполнителя в отделочных составах для ячеи-

стого строительного композита. Часть 1 [Текст] / С.А. Удодов, В.Ф. Черных // Сухие строи-

тельные смеси, 2008. – №2. – С. 68-70.

6. Стрелов, К.К. Теоретические основы технологии огнеупорных материалов [Текст] /

Стрелов К.К., Кащеев И.Д. М.: Металлургия, 1996. – 608 с.

7. Патент 201610796 РФ. Программа для моделирования хаотичной упаковки 2х-

фракционной смеси гранул [Текст] / Белов В.В, Образцов И.В., Реунов А.Г.; заявитель и па-

тентообладатель Тверской гос. тех. университет – №2009616803, зарегистрировано 25.01.10.

8. Волошин, В.П. Исследование структуры пор в компьютерных моделях плотных и

рыхлых упаковок сферических частиц [Текст] / В.П. Волошин, Н.Н. Медведев, В.Б. Фенело-

нов, В.Н. Парман // Журнал структурной химии, 1999. – Т. 40. – №4. – С. 46-60.

9. Bornemann, R., Schmidt, M.: Grundlagen und Strategien zur Verbesserung erdfeuchter

Betone, Teil I. Betonwerk + Fertigteil-Technik, Heft 8, 2005, pp. 44-51.

10. Белов, В.В. Формирование оптимальной макроструктуры строительной смеси

[Текст] / В.В. Белов, М.А. Смирнов // Строительные материалы. – 2009. – №9. – С. 88-90.

11. Белов, В.В. Капиллярное структурообразование в дисперсных системах, применяе-

мых для производства строительных материалов // Известия вузов. Строительство. – 2002. –

№9. – С. 46-51.

12. Белов, В.В. Оптимизация гранулометрического состава сырьевых смесей для по-

лучения прессованных бетонов на цементной связке [Текст] / В.В. Белов, М.А. Смирнов //

Нанотехнологии в строительстве: научный Интернет-журнал, 2010. – №2(6). – С. 7-18.