Вестник отделения строительных наук РААСН 2011 №15

Подождите немного. Документ загружается.

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

200

_________________________________________________________________________________________________________________

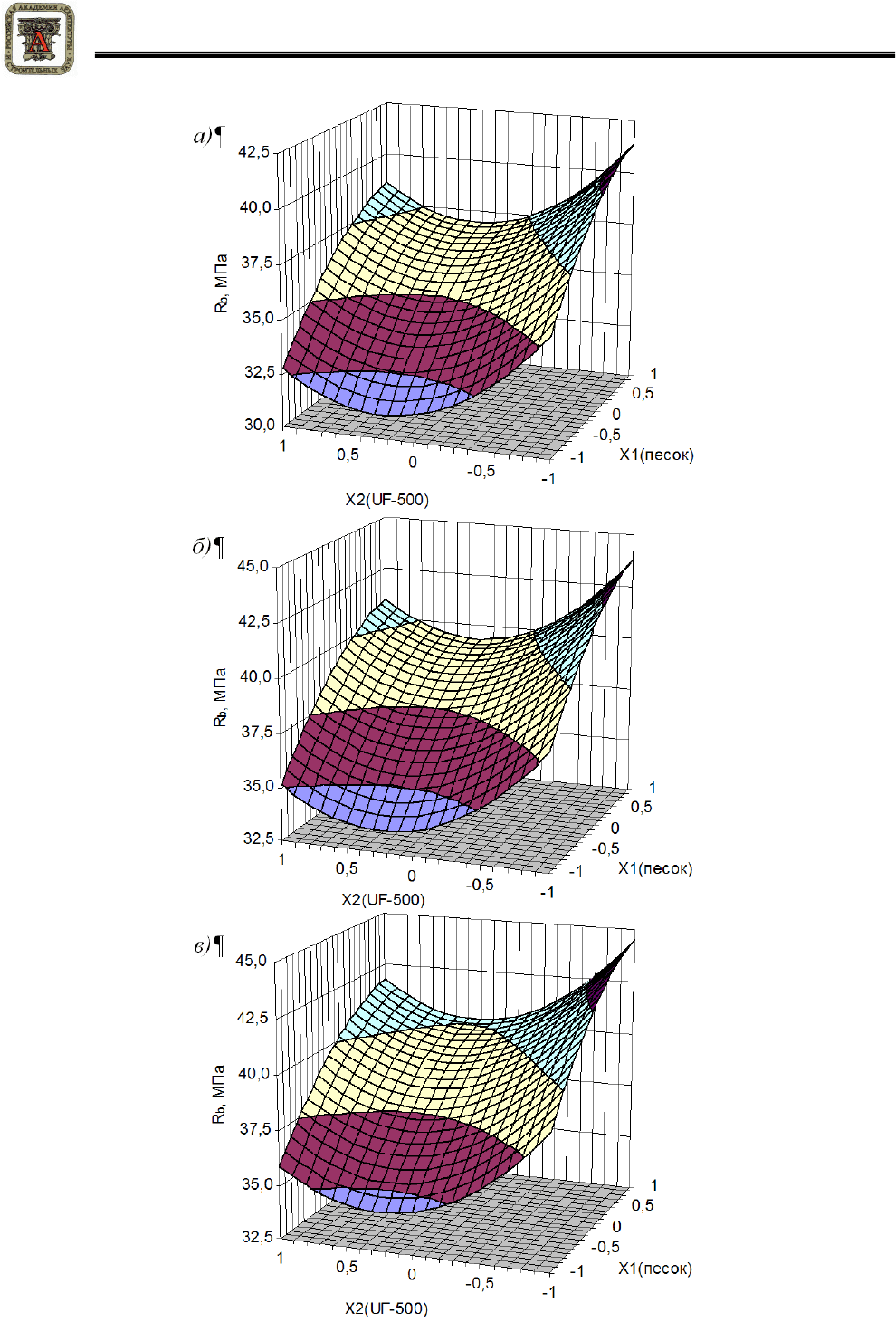
Рисунок 2 – Прочность композиций при сжатии: а – при Х

−−−−

1; б

−−−−

= 0; в

−−−−

= 1

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

_________________________________________________________________________________________________________________

201

На втором уточняющем этапе составы готовили по матрице полнофакторного плана

эксперимента ПФЭ 2

. Ошибку эксперимента определяли по нулевой точке, в которой вы-

полняли 3-и замеса.

В качестве изменяемых факторов на кодированных уровнях −1, 0 и +1 приняли: со-

держание песка Х

= 100, 130 и 160 мас. ч.; количество дисперсной арматуры UF-500 Х

= 1,2,

1,8 и 2,4 мас. ч. Время перемешивания смеси и количество отвердителя (лимонная кислота)

были постоянными и равными соответственно 6 мин и 3 мас. ч. на 100 мас. ч. связующего.

Технология приготовления и условий твердения составов описана выше.

Были получены следующие математические модели физико-механических характери-

стик клеевых и матричных составов:

bti

= 6,61 + 1,96Х

+ 0,67Х

– 0,79Х

= 50,69 + 1,12Х

– 1,73Х

– 2,84Х

– 3,15Х

Графические зависимости прочностных характеристик уточненных составов показаны

на рисунки 3-4.

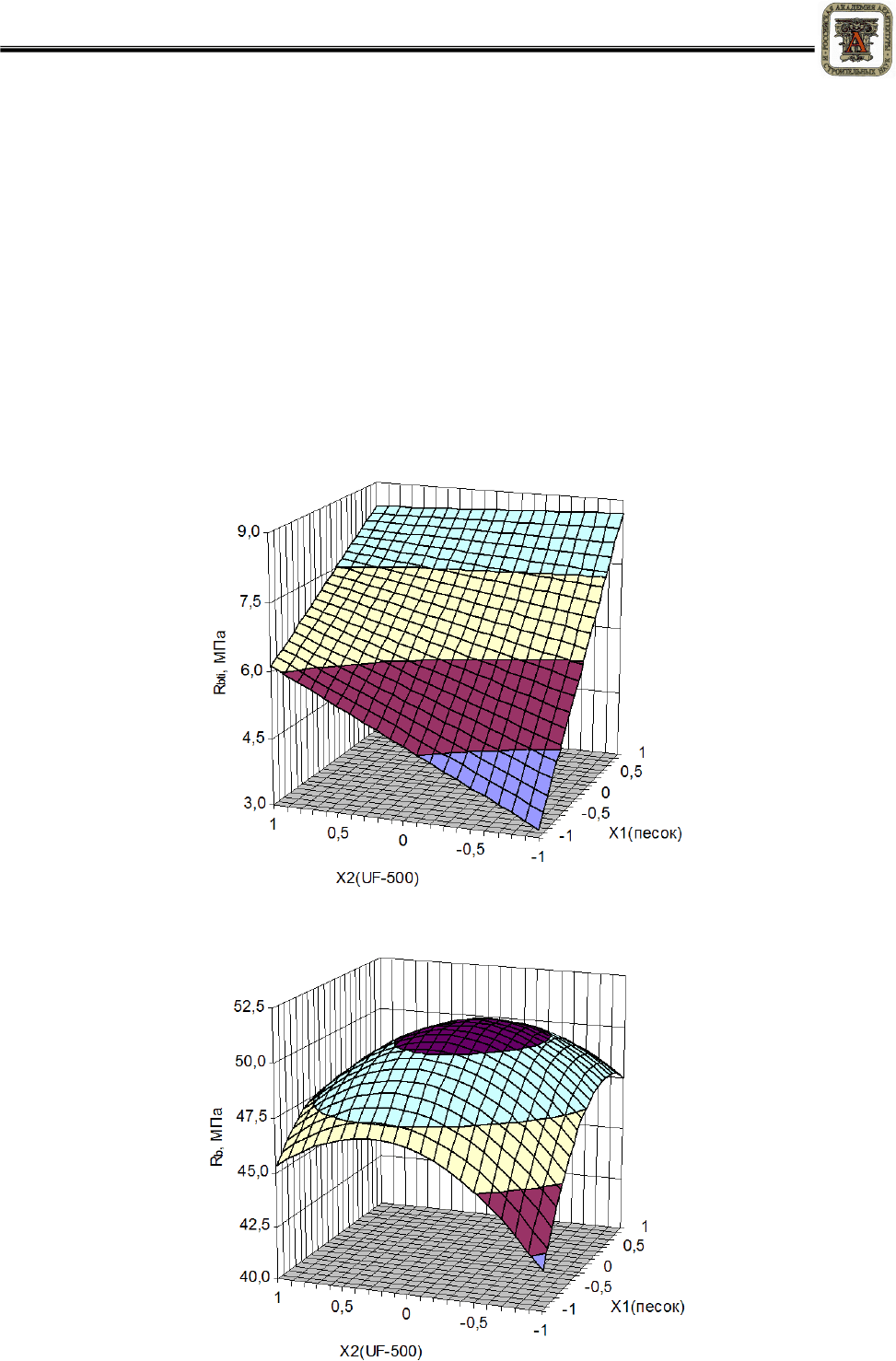
Рисунок 3 – Прочность композиций при изгибе на вяжущем ПКП-52

Рисунок 4 – Прочность композиций при сжатии на вяжущем ПКП-52

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

202

_________________________________________________________________________________________________________________

По полученным результатам можно сделать следующие выводы:

• В результате проведенных исследований поставленные цели и задачи были достиг-

нуты: изучено изменение прочностных свойства дисперсно-армированных составов клеев и

матриц в зависимости от уровней факторов, получены математические модели их свойств.

• Изменение факторов в пределах эксперимента позволило получить на втором этапе

дисперсно-армированные композиции с пределом прочности при изгибе 3,2…8,7 МПа (ми-

нимум соответствует координатам Х

= −1 и Х

= −1, максимум − Х

= 1 и Х

= −1), на сжатие –

41,9…50,8 МПа (минимум соответствует координатам Х

= −1 и Х

= −1, максимум − Х

= 0,2 и

= −0,05). По пределу прочности при изгибе оптимум достигнут не был (см. рисунок 3), а

при сжатии область оптимума достигнута (см. рисунок 4).

• Совместное введение дисперсной арматуры UF-500 и песка увеличивает прочность

клеевых и матричных композиций при изгибе, при этом эффект от введения песка, в преде-

лах изменения факторов эксперимента, больше, чем от дисперсной арматуры (коэффициент

= 1,96 > b

= 0,67).

• Введение дисперсной арматуры и наполнителя улучшают прочностные свойства и

позволяют получать эффективные композиции клеевых и матричных составов, которые

можно использовать при изготовлении каркасов и каркасных композитов.

Библиографический список

1. Каркасные строительные композиты [текст]: В 2 ч. Ч. 1. Структурообразование.

Свойства. Технология / В.Т. Ерофеев, Н.И. Мищенко, В.П. Селяев, В.И. Соломатов; Под ред.

В.И. Соломатова. – Саранск: Изд-во Мордов. ун-та, 1995. – 200 с.

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

_________________________________________________________________________________________________________________

203

УДК 625.7.06.07

ПРОКОПЕЦ В.С.

(Сибирская государственная автомобильно-дорожная академия, г. Омск)

ПОРОШКИ СТРОИТЕЛЬНОГО НАЗНАЧЕНИЯ

МЕХАНОАКТИВАЦИОННОГО СПОСОБА ПОЛУЧЕНИЯ

Создание прочных строительных материалов строительного и дорожно-строительного

назначения из низкокачественных отходов и местных материалов является актуальной зада-

чей. Практика показывает, что для ее решения необходимо улучшение свойств исходных ма-

териалов, что наиболее эффективно достигается путем интенсивного измельчения. Много-

численные исследования показывают, что при этом происходит активация материала, вели-

чина которой зависит от типа измельчительного аппарата.

В условиях многотоннажного производства в качестве механоактиватора наиболее

перспективно применение дезинтеграторов [1]. Для эффективного измельчения и активации

дезинтегратор должен быть сконструирован или настроен на измельчение определенного ма-

териала, иметь необходимую скорость вращения роторов, количество рядов бил и их соот-

ветствующую конфигурацию [2].

Примем следующие допущения: частица при измельчении соударяется с каждым би-

лом одного ряда один раз и переходит на другой ряд.

Напряжения

, возникающие в частице на близком расстоянии от места контакта,

будут равны:

, (1)

где F – площадь сечения частицы на близком расстоянии от места контакта при соударении;

m – масса частицы; а

– ускорение (замедление) центра масс частицы в проекции на ось х.

Для разрушения частицы необходимо выполнение условия:

дин

≥

⋅

max

(2)

где

дин

– динамические разрушающие напряжения при ударе.

Дифференциальное уравнение центра масс частицы будет иметь вид:

−=

, (3)

где Р – реакция поверхности била при ударе.

Силу Р можно представить как функцию от a

и жесткости частицы.

Решив уравнение (3), после несложных преобразований получим условие, характери-

зующее интенсивность разрушения частицы:

дин

kkER

ρπ

⋅

⋅⋅⋅⋅⋅⋅

≥

, (4)

где Ki – коэффициент, зависящий от размеров частицы и размеров возможной площадки, в

которой возникают разрушающие напряжения при ударе; n – количество оборотов в минуту

ротора, на котором закреплены билы; R – радиус окружности ротора, на котором закреплены

билы; Е – модуль упругости материала частицы;

– плотность материала частицы; k

– ко-

синус угла падения (угол между нормалью к поверхности била и направлением вектора ско-

рости

подлета частицы); k

– коэффициент, в основном зависящий от разности скоростей

соседних рядов бил.

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

204

_________________________________________________________________________________________________________________

Из выражения (4) следует, что разрушение частиц будет наступать при достижении

числа Ki определенного значения. При меньших значениях измельчение материала будет не-

достаточным, а при больших значениях измельчение наступит не в конце цикла прохожде-

ния материала через дезинтегратор, а раньше, т.е. потребуется дополнительная энергия для

завершения цикла прохождения уже измельченного материала через дезинтегратор.

Таким образом, число Ki позволяет проектировать дезинтеграторы с оптимальными

параметрами для измельчения и активации конкретного материала.

Испытания проводились на лабораторном дезинтеграторе. Число Ki зависит от радиу-

са R ряда билов и конфигурации билов (коэффициенты k

, k

). Следовательно, каждый ряд

билов будет иметь свое значение Ki. Конфигурация билов на всех рядах была одинаковой:

использовались цилиндрические билы.

Зависимость Ki от номера ряда билов и эффективность измельчения различных мате-

риалов приведены в таблице 1.

Таблица 1 – Зависимость Ki от номера ряда билов. Эффективность измельчения мате-

риалов

Номер

ряда

билов

Среднее

значение

Эффективность

измельчения

Средний

размер

частиц

мкм

1 2 3 4 5 6

Алюминий

0,640

90,0-100,0

Измельчение

можно

увеличить

Несколь

ко

недостаточное

0,377 0,481 0,555 0,703 0,799 0,924

Цемент

1,502

38,0-60,0

Измельчение

хоро

шее

Можно

умень

шить

Наблюдается

слипание

0,887 1,131 1,305 1,635 1,879 2,175

Резина

0,333

200,0-350,0

Измельчение

недос

таточное

Имеются

крупные

частицы

0,196 0,25 0,289 0,366 0,416 0,481

Кварцевый

песок

3,576

60,0-80,0

Измельче

ние

избыточное

Сильное

слипание

частиц

2,108 2,687 3,1 3,927 4,465 5,167

Гранит

2,238

60,0-80,0

Измельче

ние

избыточное

Наблюдается

силь

ное

слипание

частиц

1,349 1,419 1,984 2,513 2,857 3,307

Из таблицы видно, что достаточное измельчение материала для шестирядного дезин-

тегратора с цилиндрическими билами и двумя роторами, вращающимися в разные стороны,

наступает при Ki

ср

близкой к единице.

Приведенные в таблице результаты хорошо подтверждаются электронными снимками

измельченного материала, например, кварцевого песка Березовского карьера Кемеровской

области (рисунок 1). В результате измельчения кварцевого песка наблюдаются аморфизация

структуры силиката, снижение истинной плотности минерального порошка. При этом про-

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ И СТРОИТ

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

_____________________________________

_______________________________________________

исходит изменение химического состава кварцевого песка в части увеличения процентного

содержания аморфизированного кварца в общей доле

Рисунок 1 –

Микрофотография кварцевого пес

А – преобразования в

жидкокристаллические частицы

решетки ис

Таблица 2 –

Изменение химического состава кварцевого песка в процессе измельчения

Скорость

измельче-

ния, с

-1

SiO

(общ)

SiO

(крист

ал)

0 93,6 93,6

16,67 93,6 93,5

33,33 93,6 89,4

50.0 93,6 82,9

1. Прокопец,

В.С. Опыт получения минерального порошка из местного сырья неп

средственно на АБЗ. Ж. [Текст В С

стве. – 1997. – №6. – С. 14-17.

2. Прокопец,

В.С. Математическая модель эффективности маханоактивационных

процессов в строительных материалах Текст В С Прокопец Т Л Иванова Строител

ные материалы, оборудование, технологии

3. Лесовик, В.С.

Минеральные порошки из кислых

В.С. Лесовик, В.С. Прокопец, П.А Болдырев Строитель

АРХИТЕКТУРЫ

СТРОИТ

ЕЛЬНЫХ

НАУК

_______________________________________________

_____________________________

исходит изменение химического состава кварцевого песка в части увеличения процентного

содержания аморфизированного кварца в общей доле

SiO

(таблица 2) [3].

Микрофотография кварцевого пес

ка посл

е измельчения в дезинтеграторе

жидкокристаллические частицы;

Б –

локальное сохр

решетки ис

ходной кристаллической матрицы

Изменение химического состава кварцевого песка в процессе измельчения

Содержание оксидов, % по массе

SiO

·2

СаО MgO

0 1,8 3,0 0,6 0,1

0,1 1,8 3,0 0,6 0,1

4,2 2,1 3,0 0,6 0,1

10,7 2,72 3,0 0,6 0,1

Библиографический список

В С Опыт получения минерального порошка из местного сырья неп

средственно на АБЗ Ж Текст] / В.С

Прокопец // Наука и практика в дорожном строител

В С Математическая модель эффективности маханоактивационных

процессов в строительных материалах [Текст] / В.С. Прокопец, Т.Л. Иванова Строител

ные материалы оборудование, технологии

XXI века, 2005. – №8. – С. 71

Минеральные порошки из кислых

природных материалов Текст

В С Лесовик В С Прокопец П.А. Болдырев // Строитель

ные материалы. –

2005

_____________________________

205

исходит изменение химического состава кварцевого песка в части увеличения процентного

таблица 2) [3].

е измельчения в дезинтеграторе:

локальное сохр

анение

Изменение химического состава кварцевого песка в процессе измельчения

∑

кг/м

0,2 99,5 2600

0,1 99,32 2660

0,1 99,4 2520

0,1 99,52 2430

В С Опыт получения минерального порошка из местного сырья неп

о-

Прокопец Наука и практика в дорожном строител

ь-

В С Математическая модель эффективности маханоактивационных

процессов в строительных материалах Текст В С Прокопец Т Л Иванова // Строител

ь-

73.

природных материалов [Текст] /

2005

. – №8. – С.44-45.

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

206

_________________________________________________________________________________________________________________

УДК 691.16

СЕЛЯЕВ В.П., УТКИНА В.Н., СЕЛЯЕВ П.В.,

КОРОВИНА О.Ю., КЕЧУТКИНА Е.Л.

(Мордовский государственный университет им. Н.П. Огарева, г. Саранск)

ВРЕМЕННАЯ ЗАВИСИМОСТЬ ПРОЧНОСТИ КОМПОЗИЦИОННЫХ

МАТЕРИАЛОВ ПРИ СОВМЕСТНОМ ДЕЙСТВИИ АГРЕССИВНЫХ

СРЕД И ТЕМПЕРАТУРЫ

Временная зависимость прочности полимеров получена С.Н. Журковым [1, 2] на осно-

вании анализа экспериментальных данных и представлена в виде функции:

,exp













−

γσ

ττ

(1)

где

– долговечность (время разрушения) материала;

– постоянная, численно близкая к

периоду тепловых колебаний атомов;

– начальный активационный барьер процесса раз-

рушения;

– постоянная, зависящая от структуры и природы материала;

– напряжение в

материале;

– постоянная Больцмана;

– абсолютная температура.

Признано, что зависимость (1) имеет фундаментальное значение, т.к. эксперимен-

тально соблюдается для самых разнообразных материалов (металлы, неорганические и орга-

нические стекла, кристаллические ориентированные полимерные материалы и волокна, це-

ментные композиты) в широком интервале времени и температуры. При

уравнение (1)

по мнению В.Н. Манина, А.Н. Громова [3] теряет смысл. Этот недостаток формулы (1) обу-

словлен предположением, что временной характер процесса разрушения зависит только от

температуры и напряжения [3]. Однако на практике мы часто наблюдаем случаи разрушения

материала под действием агрессивных сред при нулевом уровне напряжений.

В работе [9] впервые сделана попытка теоретически получить функцию временной за-

висимости прочности при совместном действии температур, агрессивных сред и механиче-

ских напряжений. Для этого была рассмотрена модель Бозе-Эйнштейна, согласно которой

распределение частиц по квантовым состояниям описывается статистикой [5], имеющей вид:













−

exp

, (2)

где

– среднее число частиц в данном квантовом состоянии с энергией

;

–

химический потенциал, как характеристика системы, введенная Гиббсом (1875), определяет

работу образования одного моля данного компонента при заданных значениях давления и

температуры. Если рассматривать химическую энергию как произведение интенсивности

свойства (

) на величину фактора емкости (экстенсивности) (

или

), то будем иметь

⋅=

(если реагирующие вещества представлены твердой фазой или жидкостью).

Если предположить, что

,exp













−

〈〈

то из выражения (2) получаем выражение

близкое к статистике Больцмана в следующем виде:

( )

,exp













−Ε

==ΕΡ

RTN

(3)

принципиальное отличие распределения Больцмана от функции (3) заключается в том, что в

первом случае разрушение рассматривается как процесс, развивающийся во времени, обу-

словленный тепловыми флуктуациями частиц и действиями механических напряжений. Во

втором случае учитывается влияние на этот процесс энергии химических связей. При дейст-

вии агрессивных сред процесс разрушения сопровождается неравномерным ослаблением по

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

_________________________________________________________________________________________________________________

207

объему химических связей. Именно этим можно объяснить более слабое проявление темпе-

ратурно-временной зависимости при действии агрессивных сред [3].

Представим разрушение материала, как постепенный процесс накопления дефектов,

повреждений во времени, активизируемый действием на материал энергии тепловой, меха-

нической, химической. Под действием механической, химической энергии снижается вели-

чина начального активационного барьера.

Рассмотрим процесс развития дефектов в структурном элементе под действием посто-

янных во времени напряжений и агрессивных сред. В соответствии с моделью, предложен-

ной в работе [6], обозначим через

– вероятность того, что в некоторой связи, соединяю-

щей две частицы, флуктуирующих с частотой

, накоплена энергия, необходимая для ее

разрыва. Тогда вероятность разрыва связи за промежуток времени

будет равна

dtP

, где

≤

dtP

. Вероятность того, что за время

обрыва связи не произойдет, определяется

выражением

(

)

−1

. Если

– число исходных нагруженных связей, то число целых свя-

зей, сохранившихся к моменту времени t, будет равно:

(

)

(

)

tPNtN

−=

Число связей, разорванных в течение интервала времени

,, ttt

∆

определяется из

уравнения:

(

)

dtPPNdN

−=− 1

(4)

Интегрируя уравнение и принимая, что

(

)

−

, получаем выражение, описы-

вающее изменение числа целых связей во времени:

(

)

(

)

,exp/

tPNtN

−= (5)

так как

≤

, то очевидно, что время до разрушения связи

можно найти из условия

ωτ

Тогда

[

]

−

⋅== PP

τωτ

, (6)

где −=

ωτ

период колебаний частиц.

Если вероятность

нахождения частицы в данном энергетическом состоянии опре-

делить статистикой Бозе-Эйнштейна (3), то получим выражение:











 −

exp

ττ

. (7)

Предполагая, что разрыв связей (отрыв частиц друг от друга) происходит при дости-

жении расстояния δ

между их центрами [8] и уровне напряжений σ, то работа e

силы

, за-

траченной на разрыв связи, равна e

=fδ

. Усилие

определяется с учетом площади связей

. Так как площадь связей пропорциональна их количеству

(

)

aNA =

, то можно запи-

сать для любого времени

, что усилие, воспринимаемое связями, равно:

(

)

{

}

σωσ

⋅−=⋅⋅= atPNatNf exp

, (8)

В предельном случае, когда

работа e

будет определяться по формуле:

−

⋅= eaN

σδ

. (9)

Тогда уравнение температурно-временной зависимости прочности с учетом энергии

механической e

, химической e

примет вид:

5.0

exp













−⋅−

−

ceNU

µσδ

ττ

(10)

Очевидно, если в формуле (10) принять

и ввести обозначение

eaN

⋅

то

получим формулу С.Н. Журкова.

Формула (10) выведена при условии

;

const

т.е. она пригодна для оценки долго-

вечности материала в микрообъеме или при равномерном распределении агрессивной среды

в объеме образца. В реальных условиях этот случай встречается крайне редко.

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

208

_________________________________________________________________________________________________________________

Формула (10) дает возможность записать функцию долговечности в виде произведения:

ττττ

⋅⋅= (11)

где

– теоретическое значение долговечности для образца из материала с идеальной структу-

рой;

– поправка, учитывающая влияние уровня напряжений на долговечность образца;

–

поправка, учитывающая влияние концентрации агрессивной среды на долговечность образца.

Из формулы (10) следует, что













−













−













RTRT

γσ

τττ

exp;exp;exp

Из формулы (10) также можно получить функцию изменения прочности материала во

времени, которая имеет вид

γγ

−

Для анализа химического взаимодействия композиционного материала с агрессивной

средой будем использовать формулу (10) и экспериментальные данные, приведенные в рабо-

те [6]. Определение химической стойкости материала производится (ГОСТ 25881-83) по из-

менению предела прочности образцов, выдержанных в агрессивных средах при условии

constT

. С учетом этих условий формула (10) будет иметь вид:

(

)

[

]

кTuAkTcUA /exp/exp

∆=−=

µτ

, (11)

где

∆

– величина эффективного активационного барьера.

Формула (11) определяет зависимость долговечности материала от активности агрес-

сивной среды.

При нагружении образцов до разрушения сжимающей нагрузкой, используя формулу

(11), по диаграмме деформирования можно оценить, как изменился начальный активацион-

ный барьер

под действием химической энергии e

и определить уровень химической

энергии, затраченной на разрушении образца.

Рассмотрим графики деформирования, полученные в работе [6], для полиэфирных по-

лимербетонов, выдержанных в воде и в 10% водном растворе серной кислоты (рисунок 1).

Площадь, ограниченная кривой деформирования, дает возможность определить работу, за-

траченную на разрушение образца.

Под действием на композит агрессивных сред диаграмма деформирования изменяет-

ся. Анализ показывает, что с увеличением длительности экспонирования образцов происхо-

дит снижение значений модуля упругости предела прочности (см. рисунок 2, таблицу 1), но

возрастает предельная деформация (сжимаемость) материала. Каков механизм этих измене-

ний? Наблюдаемые явления могут быть обусловлены как пластификацией полимера, так

разрушением химических связей. Графики деформирования, подобные приведенным на ри-

сунке 1, дают возможность оценить, как меняется работа разрушения во времени под дейст-

вием воды и водного раствора серной кислоты.

Для этого, следуя работе [7], предположим, что диаграмма работы (деформирования)

материала описывается кубической параболой вида:

εεεσ

EBE −=−=

(12)

где – начальный модуль упругости; – предел прочности материала. Тогда работу де-

формации будем определять по формуле, которая с учетом выражения (12) примет вид:

εσ

вu

−==

∫

, (13)

где – относительная деформация, соответствующая значению напряжения (см. ри-

сунок 1, таблицу 1).

Графики изменения работы разрушения при действии на полиэфирные композиты во-

ды и водного раствора серной кислоты показаны на рисунке 3. Работа (А) рассчитывалась по

вu

РОССИЙСКАЯ

АКАДЕМИЯ

АРХИТЕКТУРЫ

СТРОИТЕЛЬНЫХ

НАУК

МОСКВА

–

ОРЕЛ

–

КУРСК

, 2011

_________________________________________________________________________________________________________________

209

формуле (13) и экспериментальным данным, которые принимались по графикам деформиро-

вания (рисунок 1) и данным таблицы 1.

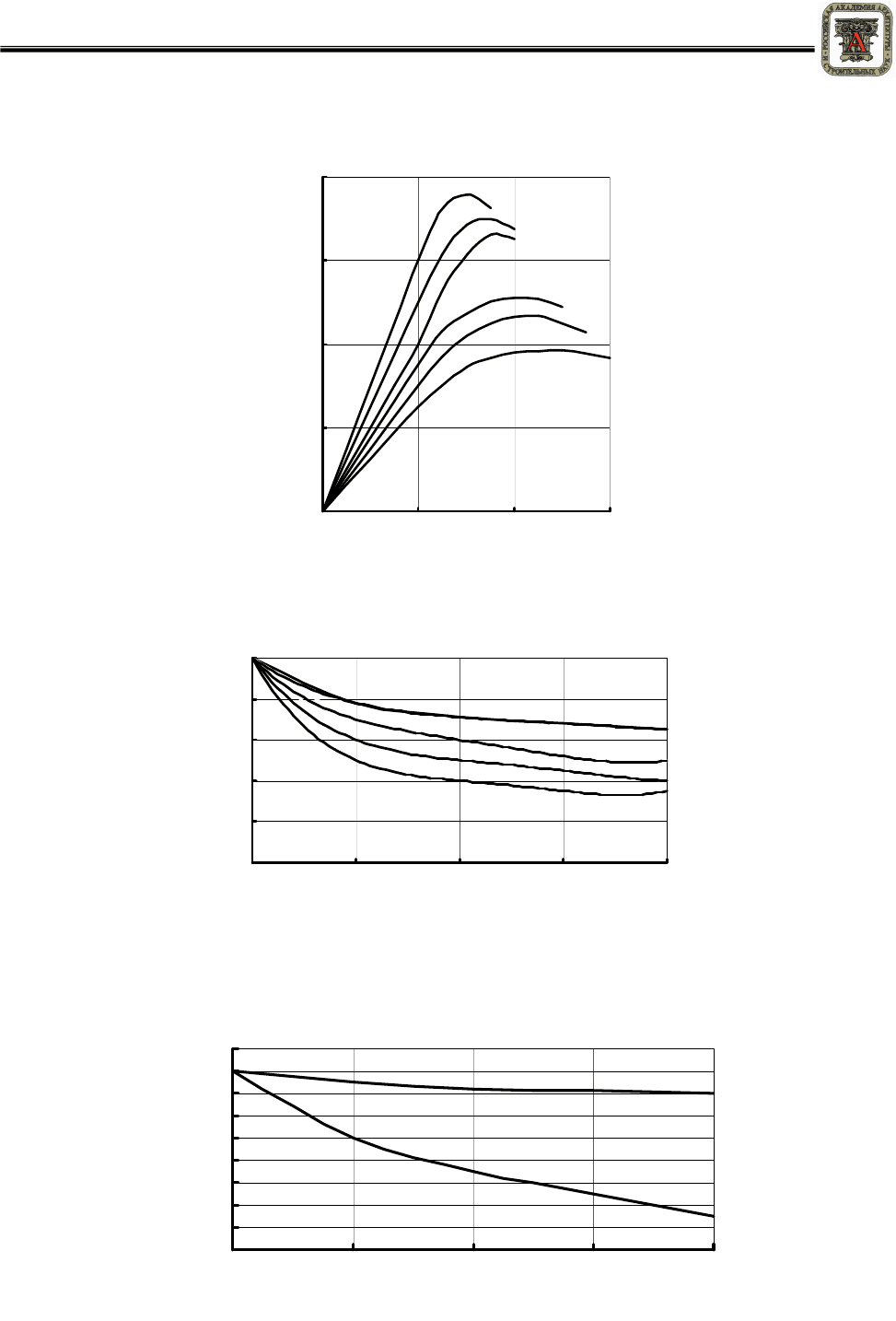
Рисунок 1 – Диаграмма «σ-ε» при сжатии образцов полиэфирного композита состава 4

Время выдержки в воде, в сут.: 1 – 0; 2 – 15; 3 – 30; 4 – 175; 5 – 265; 6 – 400

Рисунок 2 – Кинетика изменения модуля (Е, отн. ед.) и предела прочности при сжатии образцов

(σ, отн. ед.) полиэфирных композитов выдержанных: 1 – (σ) в воде; 2 – (σ) в 10%-ном водном

растворе серной кислоты; 3 – (Е) в воде; 4 – (Е) в 10 %-ном водном растворе серной кислоты

Рисунок 3 – Кинетика изменения работы разрушения полиэфирных композитов,

выдержанных в воде (1) и 10%-ном водном растворе серной кислоты (2)

120

160

0 4 8 12

G,МПа

ε,%

0,2

0,4

0,6

0,8

0 100 200 300 400

t,сут.

отн.ед.

х х

4,1

4,2

4,3

4,4

4,5

4,6

4,7

4,8

4,9

0 100 200 300 400

t,сут.

работа разрушения