Васин С.А., Ушакова И.В. и др. Основы черчения и начертательной геометрии

Подождите немного. Документ загружается.

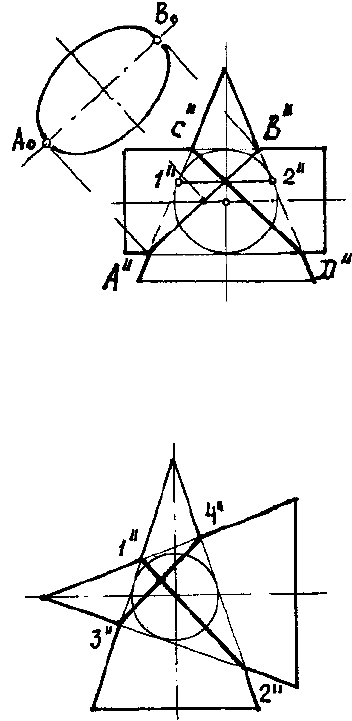
Рис. 153

На рис. 161 даны два конуса, описанные вокруг одного и того же шара. Оси кото-

рых пересекаются под прямым углом. Построить линию пересечения заданных поверхно-

стей.

Рис. 154

Наивысшие 1, 3 и наинизшие 2, 4 точки линии перехода находят в пересечении

крайних образующих на фронтальной проекции заданных поверхностей. Если сфера каса-

ется обеих поверхностей, то линия их пересечения распадается на две плоские кривые (в

нашем примере – на два различных эллипса). На фронтальной проекции эти эллипсы изо-

бражаются отрезками прямых, а на

горизонтальной – эллипсами.

Точки 5 и 6 пересечения эллипсов находят на окружности радиуса c”/2. Построе-

ние промежуточных точек ясно из чертежа.

Для определения видимости линий пересечения на горизонтальной проекции про-

водят секущую плоскость Р (через ось конуса с вершиной S). Точки 7, 8 и 9, 10 служат

границами раздела между видимой и невидимой частями линий пересечения.

На фронтальной проекции невидимая часть линии пересечения сливается с видимой.

Прямые 1-4 и 2-3 – большие оси эллипсов. Прямые 5-6 и 11-12 -- малые оси эллип-

сов.

На рис. 162 даны два цилиндра с одинаковыми диаметрами. Оси цилиндров пере-

секаются под прямым углом.

Здесь в пересечении цилиндров получаются два одинаковых эллипса 1-2 и 3-4, ко-

торые проецируются на плоскость V в виде

прямых, а на плоскость Н – в виде окружно-

стей, сливающихся с проекцией основания одного из цилиндров.

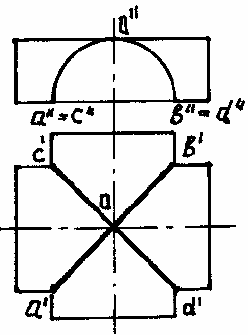
Рис. 155

Лекция № 27.

План:

27,1. Общие положения

27.2. Аналитический способ

27.3. Способ триангуляции (треугольников)

27.4. Способ нормального сечения

РАЗВЕРТКИ ПОВЕРХНОСТЕЙ

27.1. Общие положения

Под развертыванием следует понимать совмещение всей поверхности тела с плос-

костью.

РАЗВЕРТКОЙ называется фигура, в которую преобразуется при совмещении с

плоскостью поверхность, подразумеваемая как гибкая, но нерастяжимая и несжимаемая

пленка.

Развертываемые поверхности могут быть развертывающимися и неразверты-

вающимися.

К РАЗВЕРТЫВАЮЩИМСЯ относятся такие поверхности, которые могут быть со-

вмещены с плоскостью без разрывов и складок. К этому типу относятся все многогранные

поверхности. Разверткой многогранной поверхности является плоская фигура, полученная

последовательным совмещением с одной и то же плоскостью всех ее граней. Поэтому по-

строение развертки многогранной поверхности сводится к определению натурального ви-

да ее отдельных граней.

Из кривых поверхностей к числу развертывающихся относятся только те линейча-

тые поверхности, у которых касательная плоскость во всех точках одной и той же обра-

зующей постоянна. Если же у линейчатой поверхности в различных точках одной и той

же образующей разные касательные плоскости, то она не развертывается и называется ко-

сой поверхностью.

Таким образом, к числу развертывающихся линейчатых поверхностей относятся

цилиндрические (рис. 163а), конические (рис. 163б) и торсы (рис. 163в).

а) б) в)

Рис. 156

Все остальные кривые поверхности не развертываются на плоскость и поэтому при

необходимости изготовления этих поверхностей из листового материала их приближенно

заменяют развертывающимися поверхностями.

СВОЙСТВА РАЗВЕРТОК:

1) каждой точке поверхности соответствует единственная точка ее развертки;

2) длина линии на развертке равна длине соответствующей линии на поверхности;

3) на развертке сохраняются величины плоских углов.

Построение развертки может быть осуществлено различными способами, как ана-

литически, так и графически.

27.2. Аналитический способ

Этот способ заключается в нанесении на чертеж развертки всех предварительно

вычисляемых размеров, необходимых для раскроя материала.

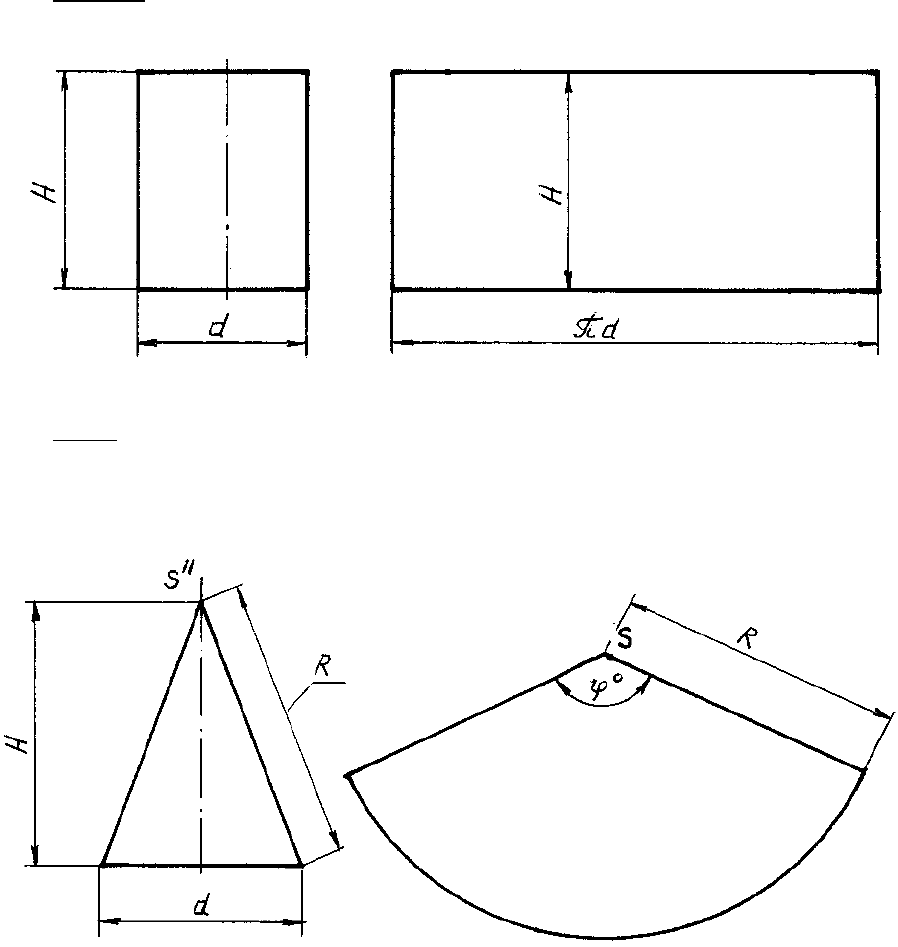
Цилиндр. Развертка боковой поверхности прямого кругового цилиндра (рис. 164)

представляет собой прямоугольник, высота которого равна высоте цилиндра (H), а дли-

на – длине окружности (диаметр d) основания.

Рис. 157

Конус. Развертка прямого кругового конуса (рис. 165) представляет собой сектор

круга, радиус которого R равен длине образующей конуса, а центральный угол ϕ

опреде-

ляется формулой:

ϕ = 180

d / R .

Рис. 158

27.3. Способ триангуляции (треугольников)

Способ триангуляции (треугольников) применяется для построения разверток пи-

рамидальных, конических и других линейчатых поверхностей, кроме цилиндрических.

Сущность способа сводится к многократному построению натурального вида тре-

угольников, из которых состоит данная пирамидальная поверхность или многогранная

поверхность, вписанная (или описанная) в данную коническую или линейчатую поверх-

ность и заменяющая ее.

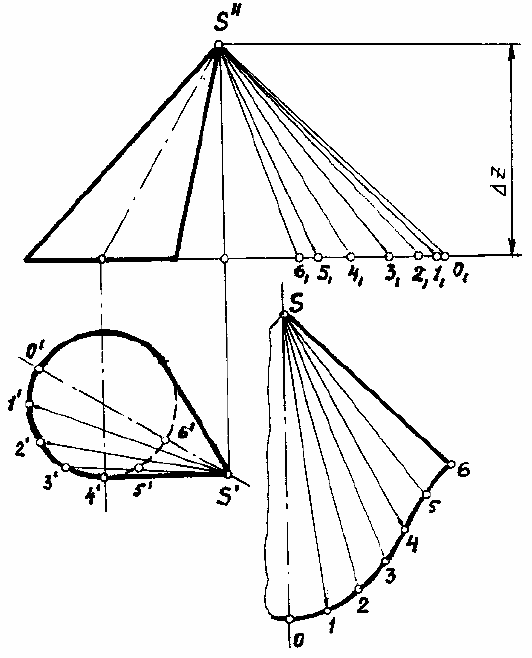
Пример. Построить развертку боковой поверхности эллиптического конуса с

круговым основанием (рис. 166).

Рис. 159

В данном примере коническая поверхность заменяется поверхностью вписанной

двенадцатиугольной пирамиды. Так как коническая поверхность имеет плоскость симмет-

рии, то можно построить развертку только одной половины поверхности. Разделив от точ-

ки О половину окружности основания конической поверхности на шесть равных частей и

определив с помощью прямоугольных треугольников натуральные величины образую-

щих, проведенных в точки деления, строим шесть примыкающих один к другому тре-

угольников с общей вершиной S (рис. 166). Каждый из этих треугольников строится по

трем сторонам; при этом две стороны равны натуральным величинам образующих, а тре-

тья – хорде, стягивающей дугу окружности основания между соседними точками деления.

После этого через точки 0,1,2,... разогнутого по способу хорд основания конической по-

верхности проводится плавная кривая (рис. 166).

27.4. Способ нормального сечения

Этот способ применяется для построения разверток призматических и цилиндриче-

ских поверхностей.

Построение сводится к многократному построению натурального вида трапеций,

из которых состоит данная призматическая поверхность, или призматическая поверх-

ность, вписанная (или описанная) в данную цилиндрическую поверхность и заменяющая

ее. Если, в частности, призматическая или цилиндрическая поверхности ограничены па-

раллельными основаниями, то трапеции, на которые разбивается поверхность, обращают-

ся в прямоугольники или параллелограммы, в зависимости от того, перпендикулярны или

нет плоскости оснований боковым ребрам или образующим поверхности.

Построение трапеций или параллелограммов проще всего произвести по их осно-

ваниям и высотам, причем необходимо также знать отрезки оснований, на которые они

делятся высотой. Поэтому для построения развертки призматической или цилиндрической

поверхности необходимо предварительно определить натуральный вид нормального сече-

ния данной поверхности. Стороны этого сечения и будут высотами трапеций или парал-

лелограммов, из которых состоит поверхность. Этот способ называется СПОСОБОМ

НОРМАЛЬНОГО СЕЧЕНИЯ.

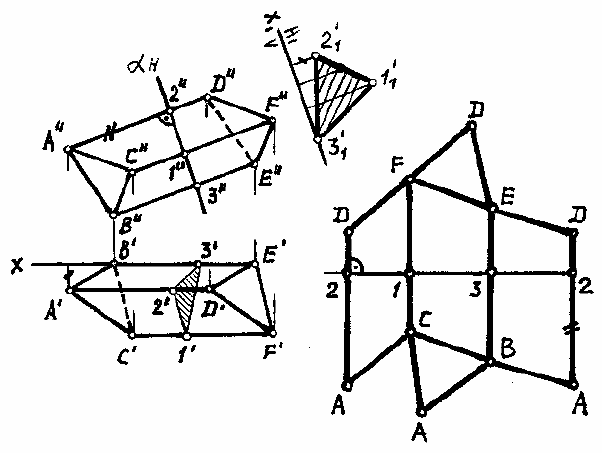
Пример. Построить развертку поверхности треугольной наклонной призмы

АВСDEF (рис. 167).

Рис. 160

Боковые ребра призмы имеют горизонтальное расположение. Пересечем данную

призму плоскостью α(α

), перпендикулярной к боковым ребрам, и построим проекции

фигуры сечения – треугольник 1-2-3 (рис. 167).

Определим натуральные величины сторон треугольника 1-2-3 способом замены

плоскостей проекций: меняем фронтальную плоскость проекций V на новую V

таким об-

разом, чтобы плоскость α стала плоскостью уровня, для чего ось x

новой системы плос-

костей проекций H/V

проводим параллельно α

. Тогда на новой фронтальной плоскости

получим натуральную величину треугольника 1-2-3 (рис. 167).

На произвольной горизонтальной прямой построим отрезок, равный периметру

треугольника 1-2-3 (рис. 167). Отрезок 1-1 можно считать разверткой нормального сече-

ния призмы. Из всех точек (1,2,3,1) этого отрезка проводим прямые, перпендикулярные к

нему, на которых откладываем отрезки боковых ребер (натуральные величины), беря их с

горизонтальной проекции, так как они являются горизонталями. Концы отложенных от-

резков соединяем прямыми СА, АВ, FD, ... Фигура CABCFEDF представляет собой раз-

вертку боковой поверхности призмы.

Полная развертка призмы показана на рис. 167. Для построения граней основания

из точек В и С проводим дуги окружностей радиусами, равными соответственно нату-

ральным величинам ребер ВА и СА. Пересечение дуг дает точку А. Аналогичным образом

найдена точка D.

Лекция № 28.

План:

28.1. Способ раскатки

28.2. Приближенные построения разверток

28.1. Способ раскатки

Способ раскатки рекомендуется для построения развертки цилиндрической по-

верхности, когда ее образующие являются прямыми уровня, то есть параллельными одной

из плоскостей проекций.

Рассмотрим данный способ на примере эллиптического цилиндра с круговым ос-

нованием, которое проецируется на горизонтальную плоскость проекций без искажения (в

натуральную величину).

Построение развертки данного цилиндра выполняем в следующей последователь-

ности (рис. 168):

1. Делим окружность основания цилиндра на 12 равных частей.

2. Вписываем в цилиндр призму, боковые ребра которой совпадают с образующи-

ми цилиндра, проходящими через точки деления основания (рис. ).

3. Принимаем за плоскость развертки фронтальную плоскость γ (γ

), которая про-

ходит через ребро призмы, совпадающее с очерковой образующей цилиндра (1).

4. Находим натуральную величину первой грани, проходящей через ребро 1, для

чего вращаем ее вокруг фронтали 1”до уровня этой фронтали. При этом точка

2”переместится по направлению, перпендикулярному к этой фронтали в положение 2, ко-

торое найдем, если из точки 1”это направление засечем отрезком 1'2'.

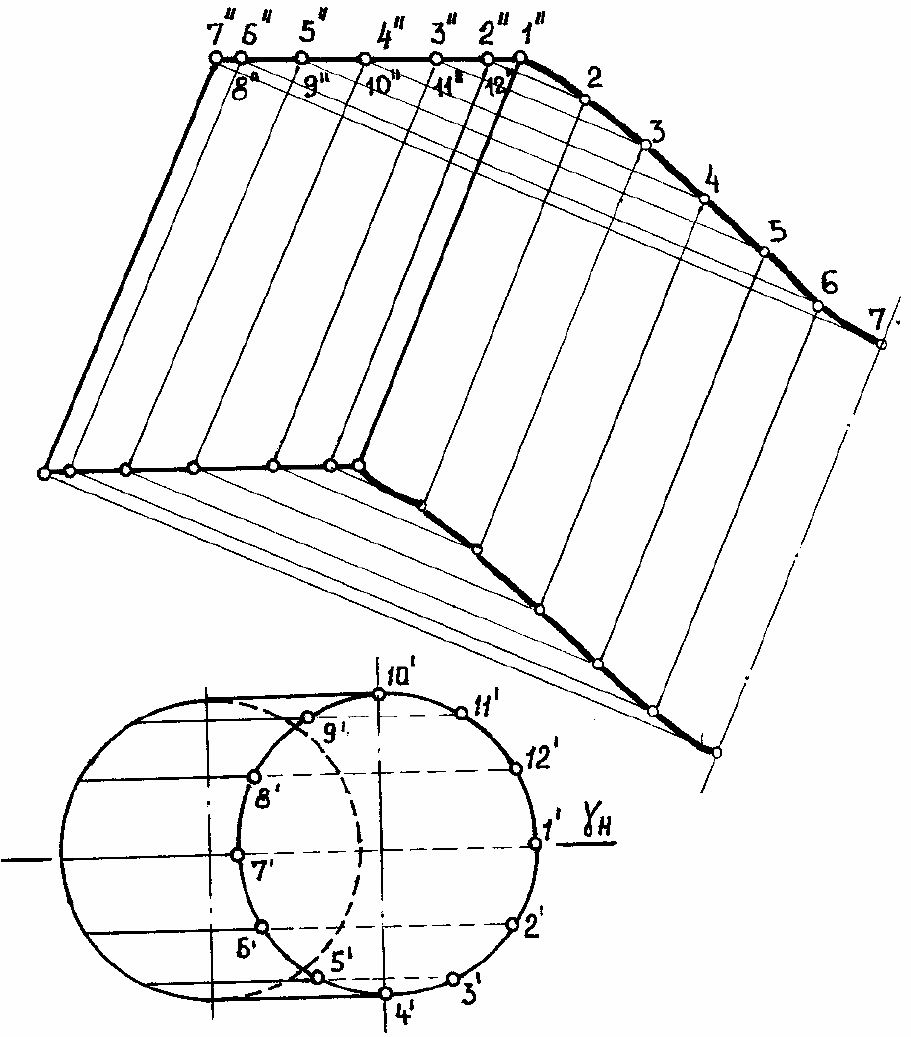
Рис. 161

Из точки 3”проводим также перпендикуляр к ребру 1(1”) и находим точку 3, отсе-

кая этот перпендикуляр из точки 2 отрезком 2'3' и т.д.

Соединяя найденные точки плавной кривой получим фигуру развертки, которую

можно представлять себе как отпечаток цилиндра, полученный путем его качения по

фронтальной плоскости, проходящей через образующую 1.

28.2. Приближенные построения разверток

Развертку неразвертывающихся поверхностей вращения строят приближенно.

1. СПОСОБ ЦИЛИНДРОВ. Способ состоит в том, что данную поверхность враще-

ния разбивают с помощью меридианов на сравнительно узкие, равные между собой доли.

Каждую такую долю заменяют описанной цилиндрической поверхностью, которая каса-

ется данной поверхности в точках среднего меридиана доли. Этот средний меридиан бу-

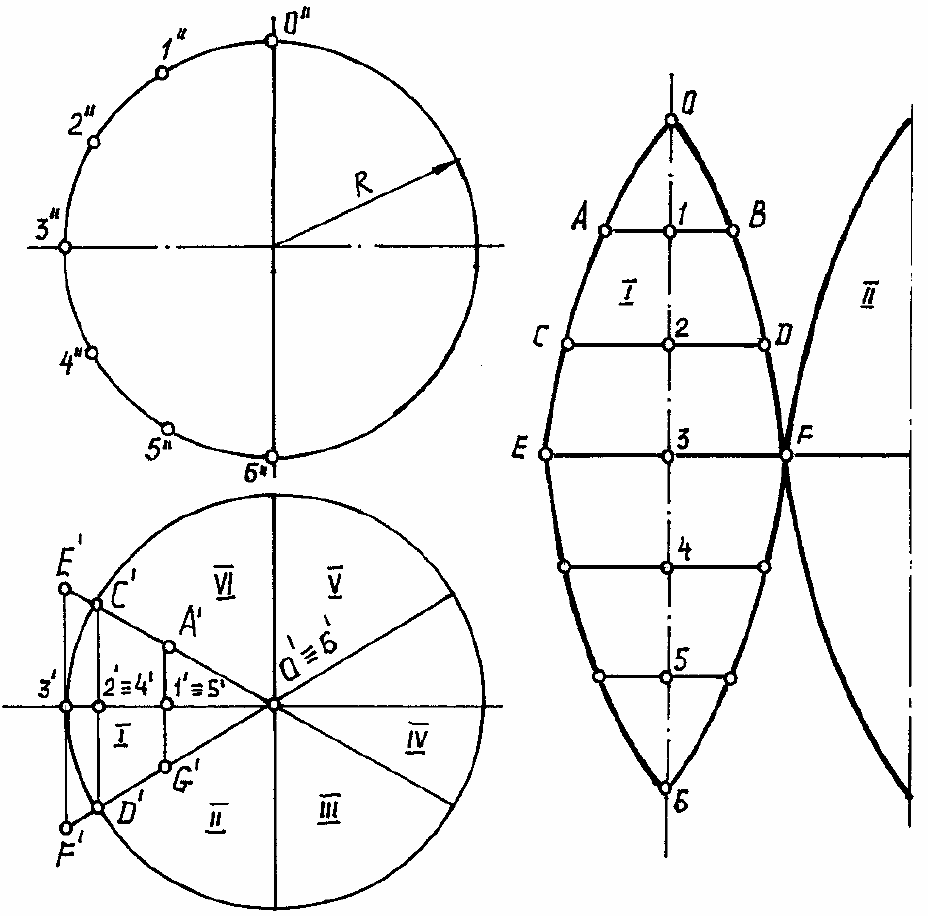
дет вместе с тем нормальным сечением цилиндрической поверхности. Границами цилин-

дрической поверхности будут плоскости меридианов, ограничивающих рассматриваемую

долю.

Пример. Построить развертку данной сферы (рис. 169). Разобьем сферу при по-

мощи меридианов на шесть равных частей. Рассмотрим построение приближенной раз-

вертки одной части сферы, средним меридианом которой является главный меридиан f.

Рис. 162

Прежде всего заменим эту часть сферы цилиндрической поверхностью, описанной

около нее. Образующие этой поверхности будут фронтально проецирующими прямыми и

поэтому проецируются в натуральную величину на горизонтальную плоскость проек-

ций H. Нормальным сечением цилиндрической поверхности будет половина главного ме-

ридиана f, а границами поверхности будут плоскости меридианов, ограничивающих рас-

сматриваемую часть.

Для построения развертки этой цилиндрической поверхности заменяем ее вписан-

ной призматической поверхностью. Для этого делим половину главного меридиана на

шесть равных частей и через точки деления проводим образующие цилиндрической по-

верхности. Затем спрямляем полумеридиан f в отрезок прямой и через его точки деления

проводим перпендикулярно к нему образующие EF = EF = E

, CD = CD = C

и т.д.

Соединив концы этих образующих плавными кривыми, получим приближенную

развертку одной доли данной сферы, равной 1/6 ее части. Развертки остальных долей яв-

ляются повторением первой.

Обычно сферу разбивают на двенадцать и более частей для получения более точ-

ной ее развертки.

2. СПОСОБ КОНУСОВ. Этот способ состоим в замене неразвертывающихся по-

верхностей такой другой поверхностью, которая составлена из нескольких конических и,

следовательно, развертываемых элементов.

Построение развертки способом конусов показано на примере поверхности враще-

ния произвольного вида (рис. 170).