Васин С.А., Ушакова И.В. и др. Основы черчения и начертательной геометрии
Подождите немного. Документ загружается.

В косоугольных проекциях коэффициент искажения данного отрезка АВ может
принимать любые числовые значения в зависимости от наклона отрезка и проецирующих
лучей к плоскости проекций. В частности, если направление отрезка совпадает с направ-
лением проецирования, то проекцией этого отрезка будет точка, а коэффициент искаже-
ния равен нулю.
В основу составления технических чертежей положен способ прямоугольных про-
екций. Предмет проецируют на взаимно перпендикулярные плоскости, при этом каждую
его сторону изображают отдельно, затем плоскости проекций совмещают в одну.
На рис. 13 даны три плоскости проекций: H – горизонтальная, V –фронтальная и W
– профильная, пересекающиеся под прямым углом по линиям x, у и z, которые называют
осями проекций (осями координат). Точку О пересечения осей называют началом ко-
ординат.
При проецировании изображаемый предмет располагают между глазом наблюда-
теля и соответствующей плоскостью проекций. На каждой плоскости проекций можно
получить измерения только по двум осям, а по третьей оси, параллельно которой ведется
проецирование, сливается в точку.
Изображение на фронтальной плоскости называют фронтальной проекцией, на го-
ризонтальной плоскости – горизонтальной проекцией, на профильной – профильной про-
екцией.
В практике изображение обращенной к наблюдателю видимой части поверхности
предмета называют видом. Каждый вид несет свою информацию. На видах должно быть
показаны и невидимые линии (отверстие в детали, например).
Лекция № 3.
План:
3.1. Аксонометрические проекции. Общие положения
3.2. Аксонометрическое проецирование
3.3. Коэффициенты искажения
3.4. Виды аксонометрических проекций
3.1. Аксонометрические проекции. Общие положения
Аксонометрическая проекция – один из способов изображения пространственных
фигур на плоскости. Этот вид проекций обладает большой наглядностью и является обра-
тимым изображением. Слово “аксонометрия” в переводе с греческого означает “измере-
ние по осям”.
3.2. Аксонометрическое проецирование
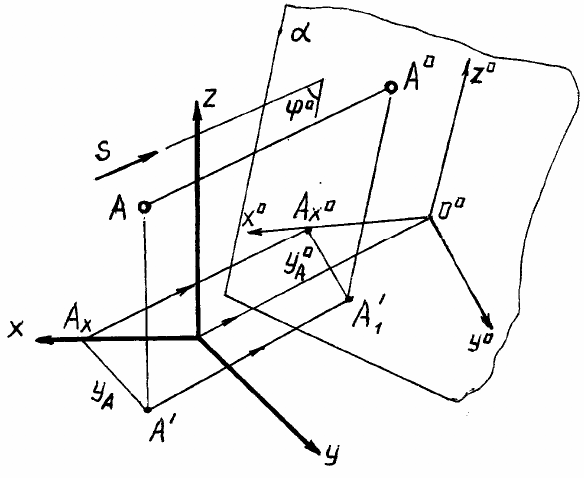
Сущность способа аксонометрического проецирования показана на рис. 8: геомет-
рическая фигура (предмет) вместе с осями прямоугольных (декартовых) координат, к ко-
торым она отнесена в пространстве, параллельно проецируется на картинную плоскость
(аксонометрическую плоскость).
Рис. 8
На рис. 8 обозначено:
α – картинная (аксонометрическая) плоскость;
x y z – натуральные (декартовы) оси координат;
s – направление проецирования;
ϕ
o
– угол проецирования;
x
o
, y
o
, z
o
– проекции натуральных осей координат на картинную плоскость – аксо-
нометрические оси;
А
o
– аксонометрическая проекция точки А;
А’
1
– вторичная проекция (горизонтальная) точки А.
Для определения точки А
o
на аксонометрической проекции (в аксонометрии) необ-
ходимо кроме аксонометрической проекции этой точки иметь ее вторичную проекцию,
например, горизонтальную А
1
, причем прямая А
o
А’
1
должна быть параллельна аксономет-
рической оси z
o
.
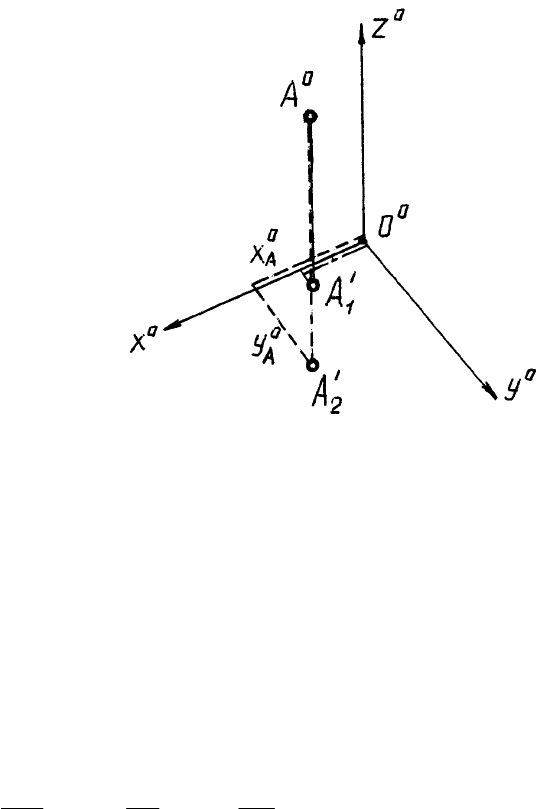
Аксонометрическая проекция точки А
o
и ее вторичная проекция А’
1
(рис. 9) одно-
значно определяют положение точки в пространстве, что делает аксонометрическую про-
екцию обратимой. Если вторичная проекция не задана, ее можно будет задать произволь-
но, например, в точке А’
2
, и тогда координаты x
А
,y
А
,z
А
изменяются.
Рис. 9
Длина отрезков натуральной координатной ломаной ОА
x
АА в общем случае не
равна длине их проекций О
o
А
o
x
А’
1
А
o
на картинной плоскости α (рис. 8).
3.3. Коэффициенты искажения
Искажение отрезков осей координат при их проецировании на картинную плос-
кость характеризуется коэффициентами искажений по аксонометрическим осям.
Коэффициентом искажения называется отношение длины аксонометрической про-
екции отрезка оси к его натуральной длине.
Коэффициенты искажения по осям O
o
x
o
, O
o
y
o
и O
o
z
o
соответственно будут равны:
K
X
X
x
A
o
A
= ; K
Y
Y
y
A
o
A
= ; K
Z
Z
z
A
o
A
= .
3.4. Виды аксонометрических проекций
Принимая различное взаимное расположение натуральной системы координат и
картинной плоскости и задавая разные направления проецирования, можно получить
множество аксонометрических проекций, отличающихся друг от друга как направлением
аксонометрических осей, так и величиной коэффициентов искажения по этим осям. В за-
висимости от соотношения коэффициентов искажения различают:
– ИЗОМЕТРИЧЕСКУЮ ПРОЕКЦИЮ (“
изос” – равный), если коэффициенты ис-
кажения по всем трем осям равны меду собой:
K
x
= K
y
= K
z
;
– ДИМЕТРИЧЕСКУЮ ПРОЕКЦИЮ, если коэффициенты искажения по двум лю-
бым осям равны между собой, а по третьей – отличаются от первых двух, например:
K
x
≠ K
y
= K
z
;

– ТРИМЕТРИЧЕСКУЮ ПРОЕКЦИЮ, если все три коэффициента искажения по
осям различны:
K
x
≠ K
y
≠ K
z
В зависимости от угла, образуемого направлением проецирования s с картинной
плоскостью α , различают:
– прямоугольную аксонометрическую проекцию, если s ⊥ α ;
– косоугольную аксонометрическую проекцию, если s
/
⊥
α .
Лекция № 4.
План:
4.1. Стандартные аксонометрические проекции
4.2. Прямоугольная изометрическая проекция
4.3. Прямоугольная диметрическая проекция
4.4. Косоугольная фронтальная диметрическая проекция
4.1. Стандартные аксонометрические проекции
Из многообразия возможных видов аксонометрических проекций ГОСТ 2.317-(СТ
СЭВ 1979-79) рекомендует для применения в чертежах всех отраслей промышленности и
строительства ограниченное количество таких, которые меньше искажают изображение
геометрических фигур и наиболее удобны при построении.
Из прямоугольных аксонометрических проекций к ним относятся изометрическая и
диметрическая проекции, из косоугольных – фронтальная и горизонтальная изометриче-
ские проекции и фронтальная диметрическая проекция.
В чертежах машиностроительной промышленности более широко применяют пря-
моугольную изометрию и диметрию, а также косоугольную фронтальную диметрию.
Все виды аксонометрических проекций характеризуются двумя параметрами: на-
правлением аксонометрических осей и коэффициентами искажения по осям.
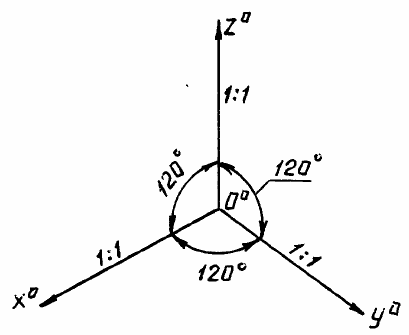
4.2. Прямоугольная изометрическая проекция
В прямоугольной изометрической проекции аксонометрические оси O
o
x
o
, O
o
y
o
и
O
o
z
o
расположены под углом 120
о
друг к другу, или, что удобно для вычерчивания, со-
ставляют угол 30
о
с горизонтальной линией (рис. 10).
Рис. 10
В прямоугольной аксонометрии сумма квадратов коэффициентов искажения равна
двум, то есть
K
2
x
= K
2
y
= K
2
z
= 2
Но в изометрии K
x
= K
y
= K
z
и, следовательно, имеем:
3K
2
x
= 2, откуда действительные коэффициенты искажения по осям равны
K
x
= K
y
= K
z
= 0,82
Так как эти значения неудобны для подсчета размеров при построении, то стандарт
рекомендует выполнять изометрическую проекцию без искажения по осям, что соответст-
вует замене действительных коэффициентов искажения более удобными приведенными
коэффициентами, равными единице:
K
x
= K
y
= K
z
= 1
При этом изображение получается увеличенным в 1,22 раза (1/0,82 = 1,22).
Прямоугольную изометрию применяют, когда все три видимые на аксонометриче-
ском изображении стороны предмета имеют примерно одинаковое количество особенно-
стей, необходимых для характеристики изображаемого предмета.
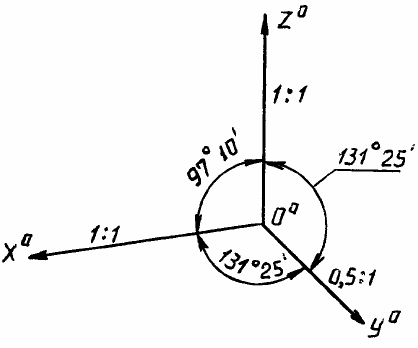
4.3. Прямоугольная диметрическая проекция
В прямоугольной диметрической проекции аксонометрические оси O
o
x
o
и O
o
z
o
со-
ставляют между собой угол 97
о
10’. Ось O
o
y
o
является биссектрисой оставшегося угла, со-
ставляя с двумя другими осями равные углы 131
о
25’ (рис. 11). При построении этой про-
екции принимают, что
K
x
= K
z
и K
y
= 0,5K
x
.
Тогда по основной теореме аксонометрии получаем из формулы
K
2
x
+ K
2
y
+ K
2
z
= 2, что 2K
2
x
+ (0,5K
x
)
2
= 2,
тогда K
2
x
= 8/9; K
x
= 0,94.
Приведенные коэффициенты искажения будут равны:
K
x
= K
z
= 1; K
y
= 0,5,
что соответствует увеличению изображения в 1,06 раза (1/0,94 = 1,06).
Рис. 11
Прямоугольная диметрия рекомендуется к применению в случае, когда наиболь-
шее число характерных особенностей сосредоточено на одной стороне предмета. Наибо-
лее отличающаяся особенностями сторона предмета располагается параллельно плоскости
X
o
O
o
Z
o
.
4.4. Косоугольная фронтальная диметрическая проекция
Аксонометрическая плоскость α располагается параллельно фронтальной плоско-
сти проекций V (рис. 12). Поэтому аксонометрические оси O
o
x
o
и O
o
z
o
параллельны декар-
товым осям Ox и Oz. Соответственно, коэффициенты искажения K
x
= K
z
. Значение K
y
при-
нимается равным 0,5. Расположение аксонометрических осей показано на рисунке.
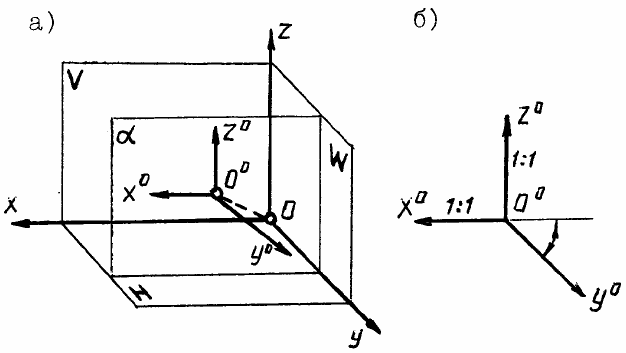
Рис. 12
Косоугольная фронтальная диметрия удобна в тех случаях, когда изображаемая
геометрическая фигура содержит большое число окружностей (или других кривых, со-
стоящих из дуг окружностей), лежащих на взаимно параллельных плоскостях. При распо-
ложении этих плоскостей параллельно аксонометрической плоскости, все окружности бу-
дут проецироваться на нее также в виде окружностей, что упрощает построение.
Лекция № 5.
План:
5.1. Комплексный чертеж точки
5.2. Проекции прямых общего положения
5.1. Комплексный чертеж точки
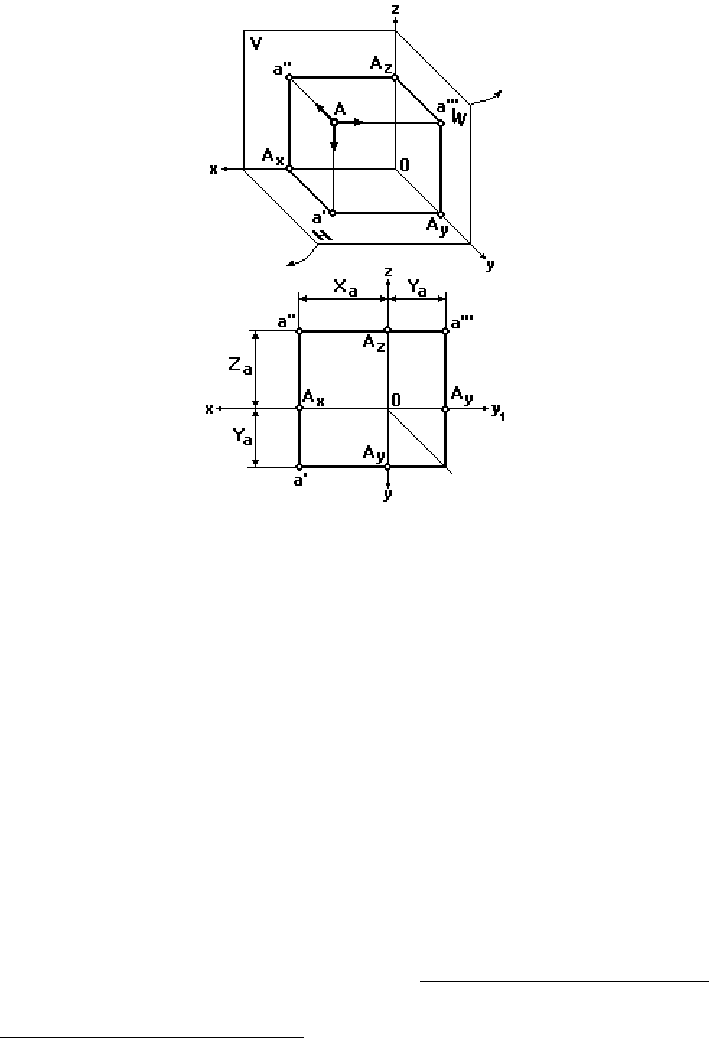
Внутри трехгранного угла, образованного горизонтальной (H), фронтальной (V) и
профильной (W) плоскостями проекций, расположим какую-либо точку А (рис. 13).
Рис. 13
Направим проецирующий луч перпендикулярно плоскости V. Точка пересечения
этого луча с плоскостью V будет фронтальной проекцией a'' точки A. Спроецируем точку
А на плоскость H и получим ее горизонтальную проекцию a'. Проецируя точку А на плос-
кость W, получим ее профильную проекцию a'''.
Для получения чертежа необходимо все три плоскости V, H и W вместе с
постро-
енными на них проекциями совместить в одну плоскость, т.е. развернуть их.
При этом плоскость H поворачивается вокруг оси x на 90 градусов книзу, плос-
кость W – вокруг оси z на 90 градусов вправо, а плоскость V остается неподвижной (при
этом ось y как бы раздваивается).
В результате совмещения получают чертеж точки в трех проекциях
. Очертания
плоскостей H, V и W на чертеже не показывают.
Линию, связывающую горизонтальную и профильную проекции точки А, пред-
ставляют двумя отрезками ломаной линии. Вершина ее лежит на биссектрисе угла, обра-
зованного осями y и y
1
. Эту биссектрису называют постоянной линией чертежа.
Прямые линии, соединяющие проекции точки и перпендикулярные осям проекций,
называют линиями проекционной связи.
Координатный отрезок, равный превышению точки А над плоскостью H, называют
высотой Za (аппликатой) точки А. Координатный отрезок, равный расстоянию от точки
А до плоскости V, называют глубиной Ya (ординатой) точки А. Координатный отрезок,
равный расстоянию от точки А до плоскости W, называют широтой Xa (абсциссой)
точки А.
Горизонтальная проекция точки А определяется на эпюре ее координатами Xa и Ya,
а фронтальная – координатами Xa и Za (рис. 13).
5.2. Проекции прямых общего положения
Ортогональной проекцией прямой на плоскость является прямая линия, за исклю-
чением того случая, когда прямая перпендикулярна к плоскости проекций.
Одна проекция прямой не определяет ее положение в пространстве. Для полного
представления о расположении прямой необходимо иметь две или три (для профильной
прямой, см. рис. 18) проекции.
Построение комплексного чертежа прямой сводится к построению проекций двух
ее точек, так как две точки вполне определяют положение прямой в пространстве (рис.
14).
Рис. 14
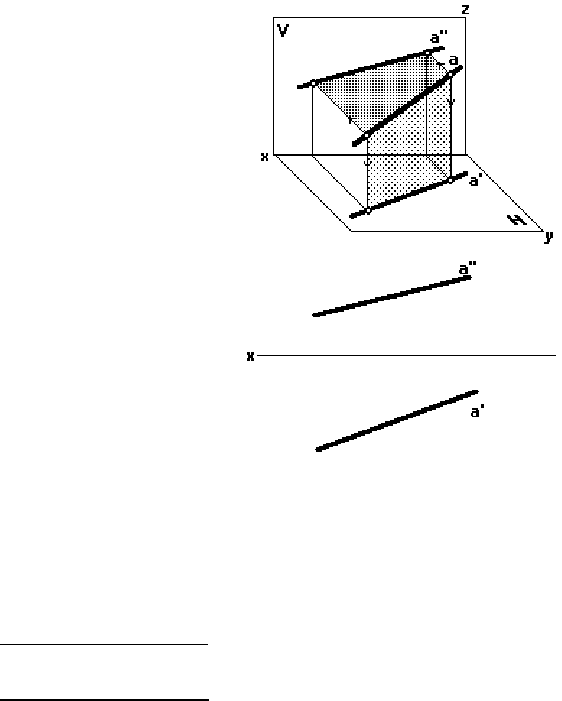
ПРЯМАЯ ОБЩЕГО ПОЛОЖЕНИЯ – это прямая, расположенная наклонно (под
произвольным углом) ко всем трем плоскостям проекций. Каждая из проекций такой пря-
мой меньше ее натуральной величины.
Прямые общего положения подразделяются на восходящие и нисходящие.
Восходящая прямая по мере удаления от наблюдателя поднимается вверх. Проек-
ции такой прямой ориентированы относительно оси x одинаково (рис. 14).
Нисходящая прямая по мере удаления от наблюдателя направлена вниз. Ее проек-
ции ориентированы относительно оси x противоположно (рис. 15).
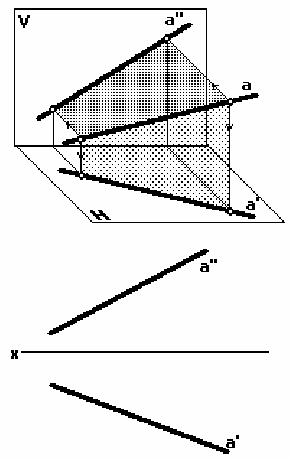
Рис. 15
