Васин С.А., Ушакова И.В. и др. Основы черчения и начертательной геометрии
Подождите немного. Документ загружается.

Лекция № 6.
План:
6.1. Проекции прямых уровня
6.2. Проекции проецирующих прямых
6.3. Определение натуральной величины отрезка прямой общего положения
6.4. Деление отрезка прямой в данном отношении
6.1. Проекции прямых уровня
Прямыми уровня называются прямые, параллельные плоскостям проекций. Их ос-
новное свойство: отрезки, принадлежащие прямым уровня, на одной из плоскостей проек-
ций (параллельной им) изображаются в натуральную величину, а на второй плоскости
проекций изображаются отрезками, параллельными осям.
Угол наклона прямой уровня к одной из плоскостей проекций на другой плоскости
проекций изображается в натуральную величину.
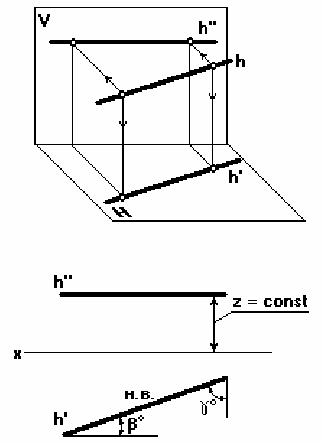
Горизонталь – прямая равных высот (рис. 16).
Это прямая (h), параллельная горизонтальной плоскости проекций.
Поскольку все точки горизонтали одинаково удалены от плоскости H, то фрон-
тальная проекция горизонтали параллельна оси x, а горизонтальная проекция горизонтали
равна натуральной величине проецируемого отрезка горизонтали (отмечено Н.В.).
Рис. 16
Угол β – угол наклона горизонтали к фронтальной плоскости проекций, а угол γ– к
профильной плоскости проекций, причем
∠β + ∠γ = 90
o
(рис. 16).
Фронталь – прямая равных глубин (рис. 17).
Это прямая (v), параллельная фронтальной плоскости проекций. Так как все точки
фронтали одинаково удалены от вертикальной плоскости V, то горизонтальная проекция
фронтали равна натуральной величине проецируемого отрезка фронтали (отмечено Н.В.).

Рис. 17
Угол α – угол наклона фронтали к горизонтальной плоскости проекций, а угол γ – к
профильной плоскости проекций, причем
∠α + ∠γ = 90
o
(рис. 17).
Профильная прямая – прямая равных широт (рис. 18).
Это прямая (w), параллельная профильной плоскости проекций.
Поскольку все точки профильной прямой одинаково удалены от плоскости проек-
ций W, то горизонтальная и фронтальная проекции профильной прямой перпендикулярны
оси x, а профильная проекция равна натуральной величине проецируемого отрезка этой
прямой (отмечено Н.В.) (рис. 18).
Рис. 18
Углы α и β – углы наклона профильной прямой к горизонтальной (H) и фронталь-
ной (V) плоскостям проекций, причем
∠α + ∠β = 90
o
.
6.2. Проекции проецирующих прямых
Проецирующей называется прямая, перпендикулярная к плоскости проекций.
Проецирующая прямая проецируется на одну плоскость проекций (перпендику-
лярную ей) в точку, а на другую – в прямую, перпендикулярную соответствующей оси.
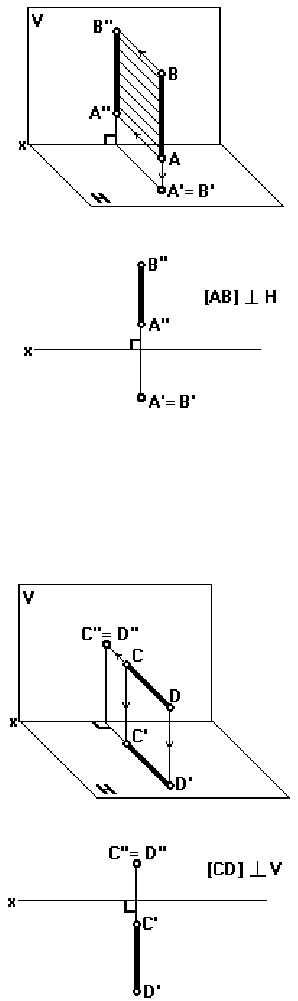
Горизонтально-проецирующая прямая (рис. 19).
Это прямая, перпендикулярная к горизонтальной плоскости проекций. Ее горизон-
тальная проекция собирает горизонтальные проекции всех точек, принадлежащих этой
прямой, например точек А и В.
Рис. 19
Фронтально-проецирующая прямая (рис. 20).
Это прямая, перпендикулярная к фронтальной плоскости проекций. Ее фронталь-
ная проекция собирает фронтальные проекции всех точек, лежащих на данной прямой,
например точек С и Д.
Рис. 20
Профильно-проецирующая прямая (рис. 21).
Это прямая, перпендикулярная к профильной плоскости проекций. Ее профильная
проекция собирает профильные проекции всех точек, лежащих на этой прямой, например
точек Е и F.
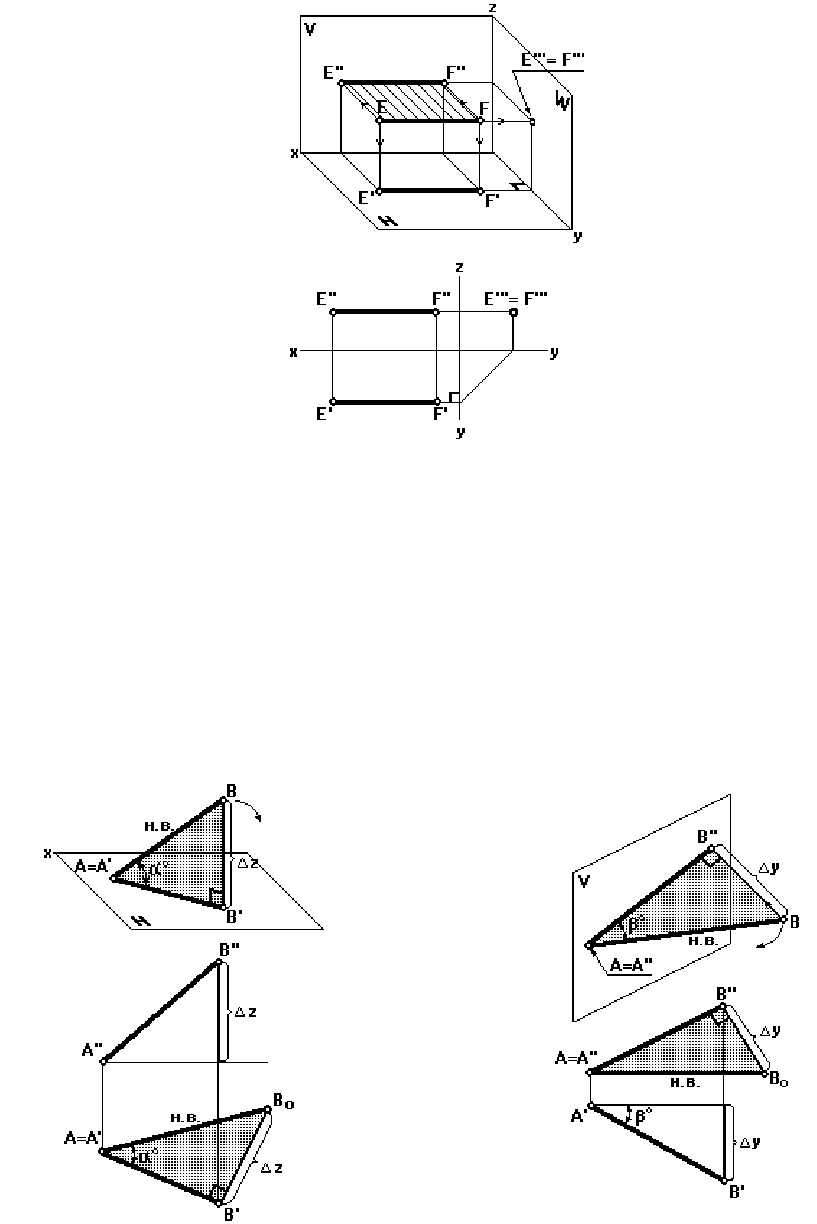
Рис. 21
6.3. Определение натуральной величины отрезка
прямой общего положения
Отрезок прямой общего положения проецируется на плоскости проекций с иска-
жением (в уменьшенном виде).
Натуральная величина отрезка на комплексном чертеже (обозначается Н.В.) стро-
ится как гипотенуза прямоугольного треугольника, первый катет которого равен одной из
проекций отрезка, а второй катет равен разности расстояний от концов отрезка до той
плоскости проекций, на которой взят первый катет (рис. 22), (рис. 23).
Рис. 22
Рис. 23
Натуральная величина угла наклона прямой к плоскости проекций может быть оп-
ределена также способом прямоугольного треугольника.
На рис. 22 показано построение натуральной величины отрезка АВ и угла его на-
клона (α) к горизонтальной плоскости проекций с помощью прямоугольного треугольни-
ка, у которого первый катет – горизонтальная проекция А'B', а второй катет – разность
расстояний от концов отрезка АВ до горизонтальной плоскости проекций, т.е. разность
высот ∆z.
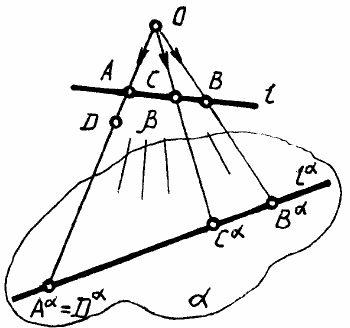
На (рис. 23) дано построение натуральной величины отрезка АВ и угла его наклона
β к фронтальной плоскости проекций с помощью прямоугольного треугольника, у которо-
го первый катет – фронтальная проекция A''B'', а второй катет – разность расстояний от
концов отрезка АВ до фронтальной плоскости проекций, т.е. разность глубин ∆y (рис. 23).
6.4. Деление отрезка прямой в данном отношении
Точка делит отрезок прямой линии в пространстве в таком же отношении, в каком
проекции точки делят одноименные с ними проекции отрезка (рис. 24).
Рис. 24
Так, например, надо разделить отрезок АВ в отношении 2:3, делящая точка лежит
на отрезке (рис. 24).
По основному положению мы должны иметь:
КА/КВ = К'А'/К'В' = К''В''/К''В'' = 2/3
На чертеже сначала определяем горизонтальную проекцию К' точки, которая делит
горизонтальную проекцию А'В' данного отрезка АВ в отношении 2:3. Для этого через точ-
ку А' проводим произвольную прямую, на которой от точки А' отложим пять равных про-
извольных отрезков (2+3=5). Далее соединяем прямой линией точки 5 и В' и проводим
прямую 2К, параллельную прямой 5В'. Точка К' разделит отрезок А'В' в отношении 2:3.
Проведя линию связи, находим фронтальную проекцию К
'' искомой точки К. Точка К''
разделит отрезок А''В'' в отношении К''А''/К''В'' = 2/3.

Лекция № 7.
План:
7.1. Параллельные прямые
7.2. Пересекающиеся прямые
7.3. Скрещивающиеся прямые
7.1. Параллельные прямые
Если провести через данные параллельные прямые АВ и СD плоскости, перпенди-
кулярные горизонтальной плоскости проекций, то эти две плоскости будут параллельны,
и в их пересечении с плоскостью H будут получены две взаимно параллельные прямые
A'B' и C'D', являющиеся ортогональными проекциями данных прямых АВ и CD на гори-
зонтальную плоскость проекций (рис. 25).
Рис. 25
Аналогичным образом можно получить и ортогональные проекции данных прямых
на фронтальную плоскость V.
На комплексном чертеже одноименные проекции параллельных прямых парал-
лельны: A'B' || C'D' и A''B'' || C''D'' (рис. 25).
7.2. Пересекающиеся прямые
Взаимно пересекающиеся прямые имеют общую точку, например, отрезки прямых
АВ и CD пересекаются в точке К. Проекции пересекающихся прямых пересекаются, и
точки их пересечения (K' и K'') лежат на одной линии связи – перпендикуляре к оси x (рис.
26).
7.3. Скрещивающиеся прямые
Это прямые, которые не параллельны и не пересекаются. На комплексном чертеже
проекции скрещивающихся прямых (прямые АВ и CD) могут пересекаться, но точки пере-
сечения (1,
2 и 3, 4) лежат на разных линиях связи (рис. 27). Точкам пересечения одно-
именных проекций скрещивающихся прямых соответствуют в пространстве две точки: в
одном случае – 1 и 2, а в другом – 3 и 4, расположенные на прямых. На чертеже точке пе-
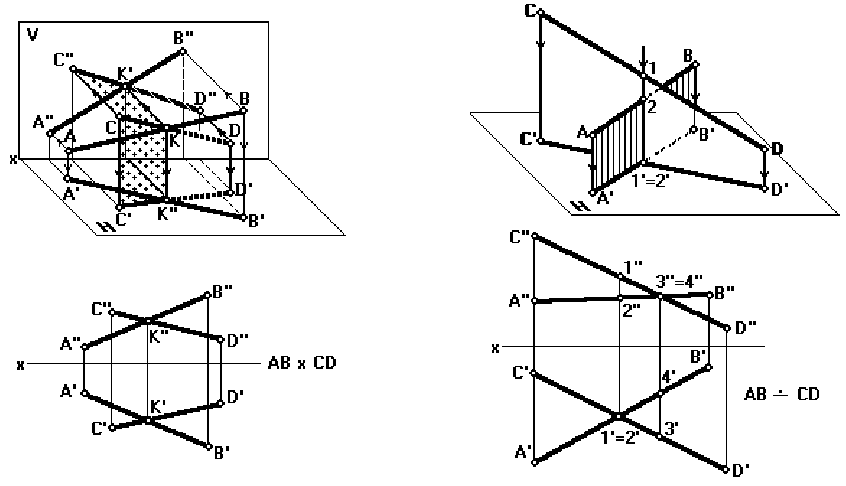
ресечения горизонтальных проекций прямых соответствует две фронтальные проекции
точек 1'' и 2''. Аналогично – с точками 3 и 4.
Рис. 26
Рис. 27
Лекция № 8.
План:
8.1. Проекции плоскостей общего положения
8.1.1. Проекции плоскостей уровня
8.1.2. Проекции проецирующих плоскостей
8.2. Проекции плоскостей уровня
8.3. Проекции проецирующих плоскостей
8.1. Проекции плоскостей общего положения
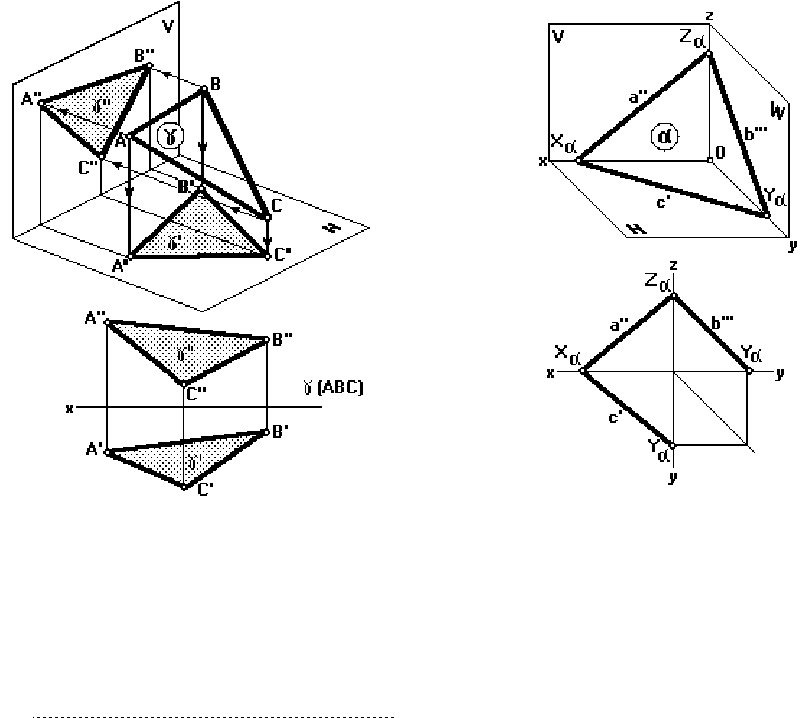
На комплексном чертеже плоскость может быть задана изображениями тех геомет-
рических элементов, которые вполне определяют положение плоскости в пространстве.
Это:
1) три точки, не лежащие на одной прямой (рис. 28);
2) прямая и точка вне прямой;
3) две параллельные прямые (рис. 25);
4) две пересекающиеся прямые (рис. 26).
При решении некоторых задач целесообразно задавать на комплексном чертеже
плоскость ее следами (рис. 29).
Рис. 28
Рис. 29
СЛЕДОМ ПЛОСКОСТИ называется прямая, по которой данная плоскость пересе-
кается с плоскостью проекций.
На рис. 29 изображена плоскость α и ее следы: с– горизонтальный; а – фронталь-
ный; b – профильный. Следы плоскости сливаются с одноименными своими проекциями:
след с = с'; след а = а''; след b = b'''. Точки Xa, Ya, Za называются точками схода следов.
8.1.1. Проекции плоскостей уровня
Плоскостями уровня называются плоскости, параллельные плоскостям проекций.
Характерная особенность этих плоскостей состоит в том, что элементы, располо-
женные в этих плоскостях, проецируются на соответствующую плоскость проекций в на-
туральную величину.
Горизонтальная плоскость (рис. 30)
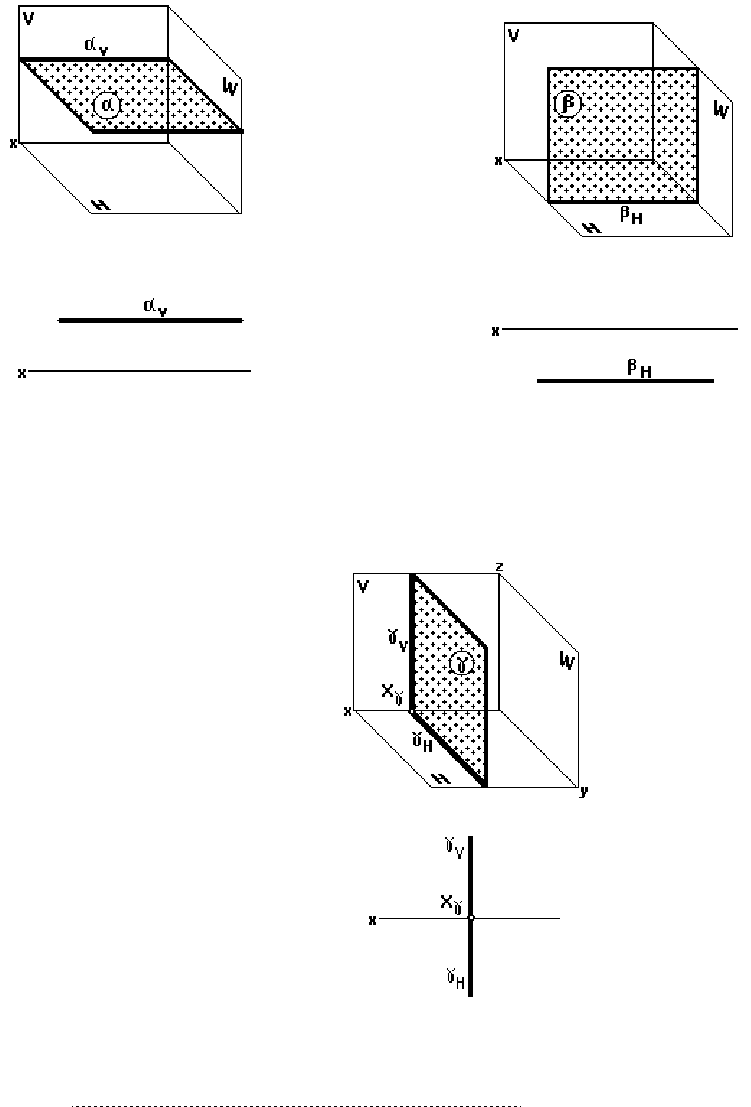
Горизонтальная плоскость параллельна горизонтальной плоскости проекций.
На двухкартинном комплексном чертеже она изображается одним фронтальным
следом, параллельным оси x.
На рис. 30 изображена горизонтальная плоскость α (α
V
).
Фронтальная плоскость (рис. 31)
Фронтальная плоскость параллельна фронтальной плоскости проекций.
На двухкартинном комплексном чертеже она изображается одним горизонтальным
следом, параллельным оси x.
На рис.31 изображена фронтальная плоскость β (β
Η
).
Рис. 30
Рис. 31
Профильная плоскость (рис. 32)
Профильная плоскость параллельна профильной плоскости проекций.
На двухкартинном комплексном чертеже она изображается двумя следами: гори-
зонтальным и фронтальным, перпендикулярными оси x.
На рис.32 изображена профильная плоскость γ (γ
H,V
).
Рис. 32
8.1.2. Проекции проецирующих плоскостей
ПРОЕЦИРУЮЩИМИ называются плоскости, перпендикулярные к плоскостям
проекций.
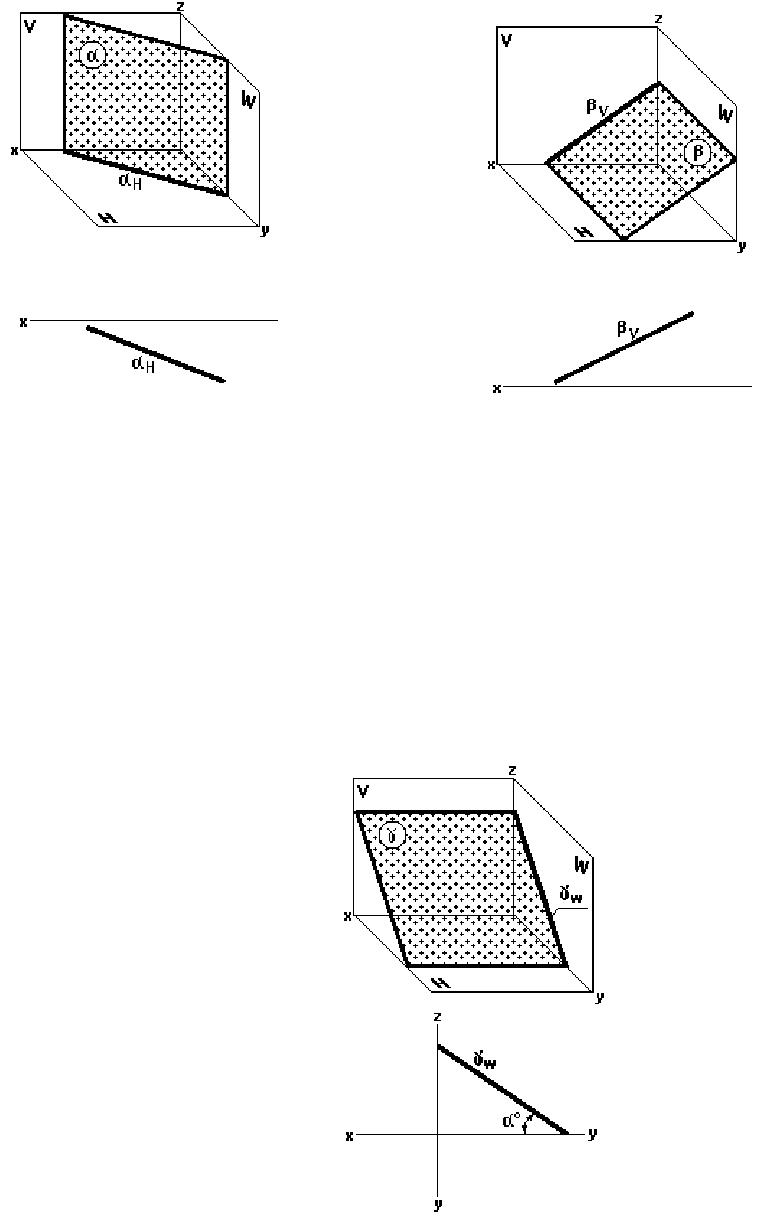
Характерной особенностью таких плоскостей является их собирательное свойство.
Оно заключается в следующем: соответствующий след – проекция плоскости – собирает
одноименные проекции всех элементов, расположенных в данной плоскости.
Горизонтально-проецирующая плоскость (рис. 33)
Горизонтально-проецирующая плоскость перпендикулярна к горизонтальной
плоскости проекций H.
Рис. 33
Рис. 34
Горизонтальные проекции всех точек, принадлежащих горизонтально-
проецирующей плоскости α, располагаются на горизонтальном следе – проекции α
H
этой
плоскости (рис. 33).
Фронтально-проецирующая плоскость (рис. 34)
Фронтально-проецирующая плоскость перпендикулярна к фронтальной плоскости
проекций V.
Фронтальные проекции всех точек, принадлежащих фронтально-проецирующей
плоскости β, располагаются на фронтальном следе – проекции β
Η
этой плоскости (рис.
34).
Профильно-проецирующая плоскость (рис. 35)
Профильно-проецирующая плоскость перпендикулярна к профильной плоскости
проекций W.
Рис. 35
