Васин С.А., Ушакова И.В. и др. Основы черчения и начертательной геометрии

Подождите немного. Документ загружается.

Профильные проекции всех точек, принадлежащих профильно-проецирующей

плоскости γ , располагаются на профильном следе – проекции этой γ

плоскости (рис. 35).

Лекция № 9.

План:

9.1. Взаимное расположение двух плоскостей

9.2. Пересечение плоскостей общего положения

9.1. Взаимное расположение двух плоскостей

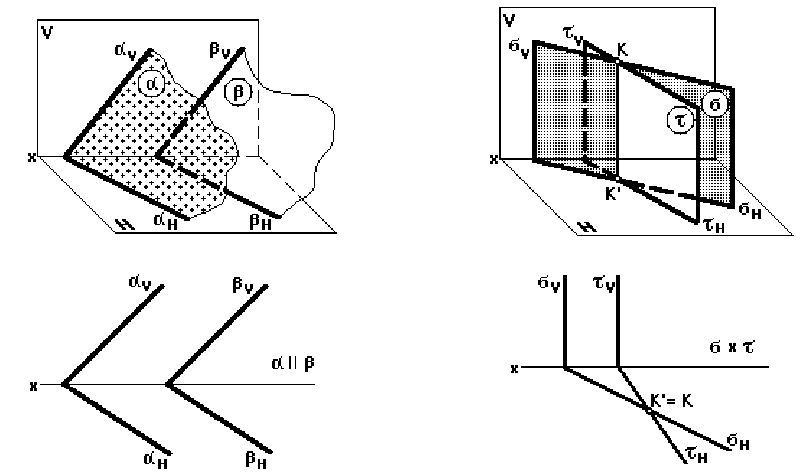
Две плоскости могут быть параллельными или пересекаться между собой.

Параллельные плоскости (рис. 36)

Две плоскости параллельны, если две пересекающиеся прямые одной плоскости

соответственно параллельны двум пересекающимся прямым другой плоскости. В качестве

пересекающихся прямых в каждой из двух параллельных плоскостей можно взять их сле-

ды.

На рис. 36 изображены две взаимно параллельные плоскости α и β , которые на

комплексном чертеже заданы следами α

и α

, и β

, β

Пересекающиеся плоскости (рис. 37)

На рисунке изображены пересекающиеся плоскости σ и τ.

Рис. 36

Рис. 37

Пересечение плоскостей подтверждается пересечением пары их одноименных сле-

дов (точка К = К').

9.2. Пересечение плоскостей общего положения

Две плоскости пересекаются по прямой линии. А поскольку прямая определяется

двумя точками, построение линии пересечения плоскостей сводится к нахождению про-

екций двух ее точек.

С этой целью применяют способ вспомогательных секущих плоскостей,

пересе-

кающих данные поверхности (плоскости) по соответствующим прямым.

ПРИМЕР. На рис. 38, 39 изображены плоскости общего положения σ(a ⎢⎢b) и

τ(E,F,K), для которых требуется найти линию пересечения.

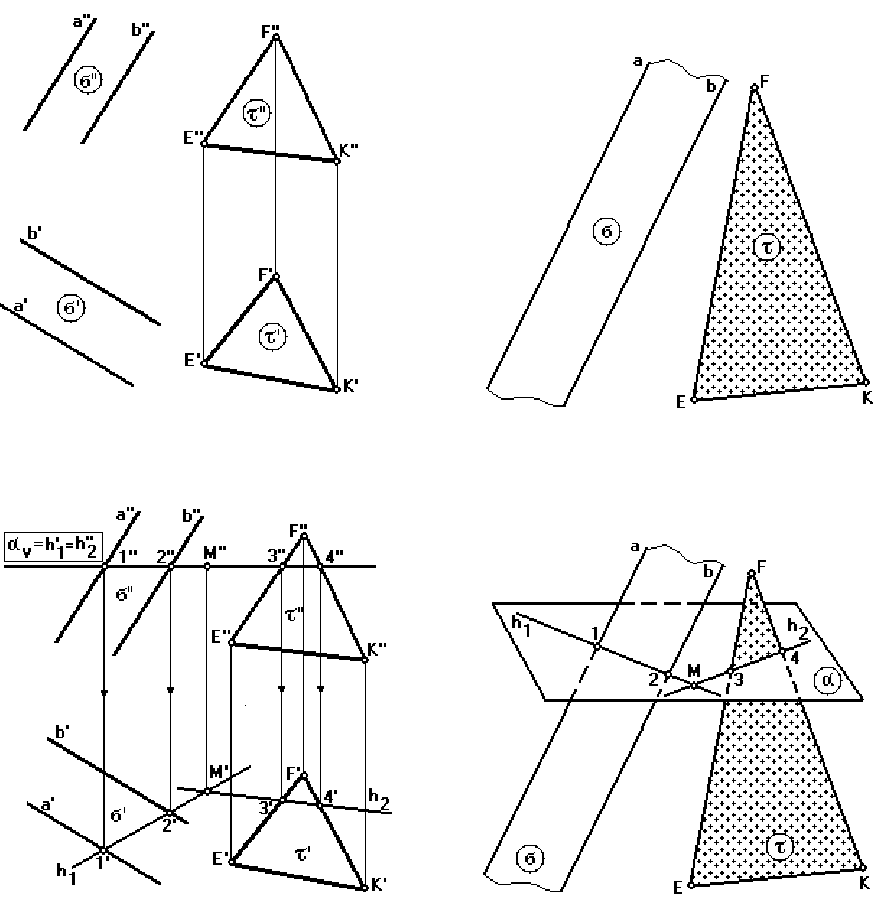
Рис. 38

Рис. 39

Нахождение общих для плоскостей σ и τ двух точек М и N проводится введением

двух горизонтальных плоскостей α и β.

Рис. 40

Рис. 41

а) Введение первой вспомогательной горизонтальной плоскости (рис. 40, 41).

Плоскость α пересекает плоскости σ и τ по горизонталям h

(прямая 1-2) и

(прямая 3-4).

Прямые 1-2 и 3-4 пересекаются в точке М, общей для плоскостей σ и τ , следова-

тельно, принадлежащей линии пересечения этих плоскостей (рис. 40, 41).

б) Введение второй вспомогательной горизонтальной плоскости (рис. 42, 43).

Плоскость β пересекает плоскости σ и τ по горизонталям h

(прямая 5-6) и h

(пря-

мая 7-8).

Рис. 42

Рис. 43

Прямые 5-6 и 7-8 пересекаются в точке N, общей для плоскостей σ и τ , следова-

тельно, также принадлежащей линии пересечения этих плоскостей (рис. 42, 43).

Рис. 44

Рис. 45

Соединив найденные точки М и N, получим искомую линию пересечения плоско-

стей σ и τ (рис. 44, 45).

Лекция № 10.

План:

10.1. Взаиморасположение прямой и плоскости

10.2. Пересечение прямой линии с плоскостью

10.3. Условие видимости на чертеже

10.1. Взаимное расположение прямой и плоскости

Возможны три случая: 1. прямая лежит в плоскости;

2. прямая параллельна плоскости;

3. прямая пересекает плоскость.

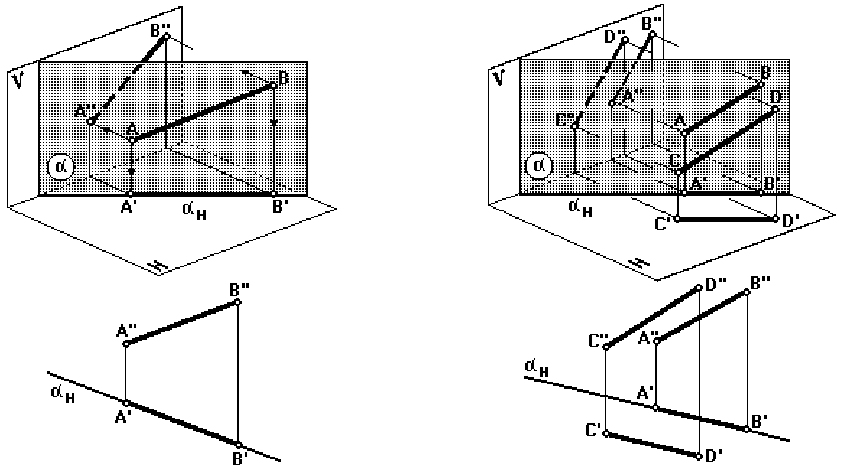
Прямая – в плоскости (рис. 46)

Прямая принадлежит плоскости, если она проходит через две точки данной плос-

кости.

Прямая, параллельная плоскости (рис. 47)

Прямая параллельна плоскости, если она параллельна какой-либо прямой этой

плоскости или принадлежит плоскости, параллельной данной.

Рис. 46

Рис. 47

Прямая пересекает плоскость (рис. 48)

Если прямая имеет с плоскостью одну общую точку, она пересекает данную плос-

кость.

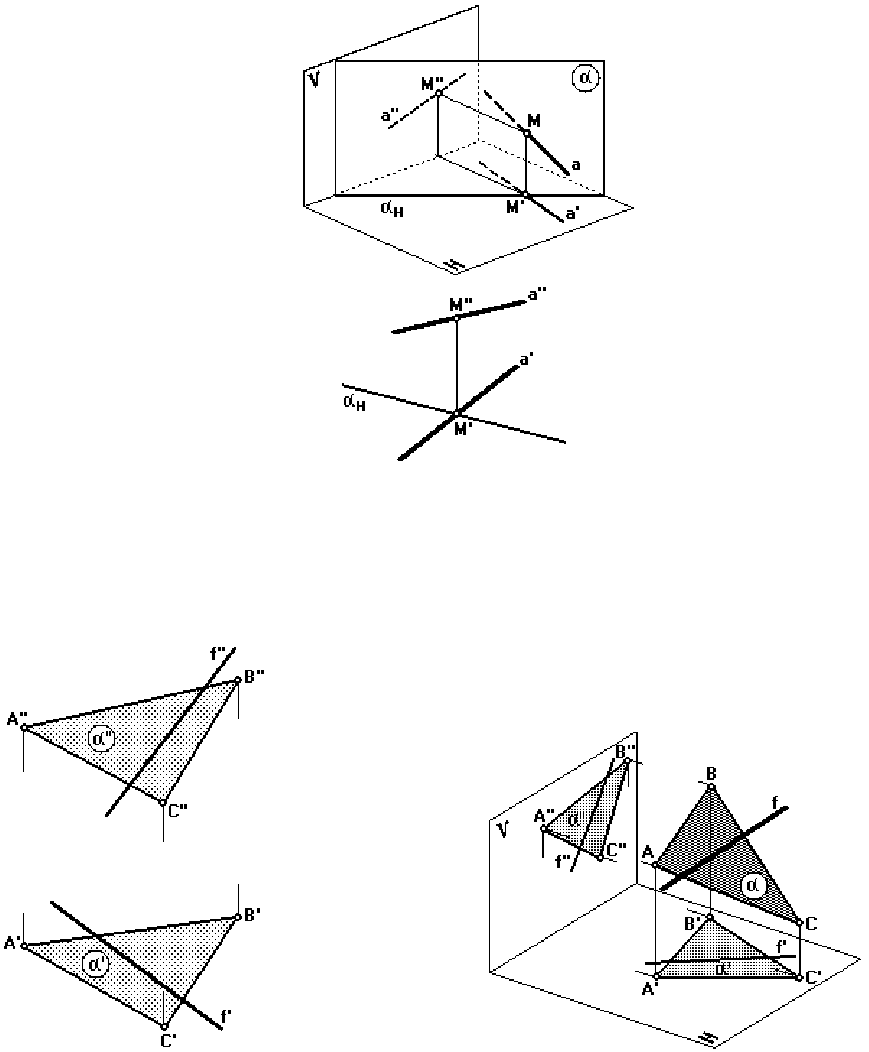
Рис. 48

10.2. Пересечение прямой линии с плоскостью

На рис. 49, 50 изображены плоскость α (АВС) и пересекающаяся с ней прямая f.

Рис. 49

Рис. 50

Для определения точки встречи прямой с плоскостью необходимо выполнить сле-

дующие операции:

1) провести через прямую вспомогательную проецирующую плоскость;

2) найти линию пересечения данной плоскости со вспомогательной плоскостью;

3) определить точку пересечения данной прямой с найденной линией пересечения

плоскостей.

1 этап (рис. 51, 52)

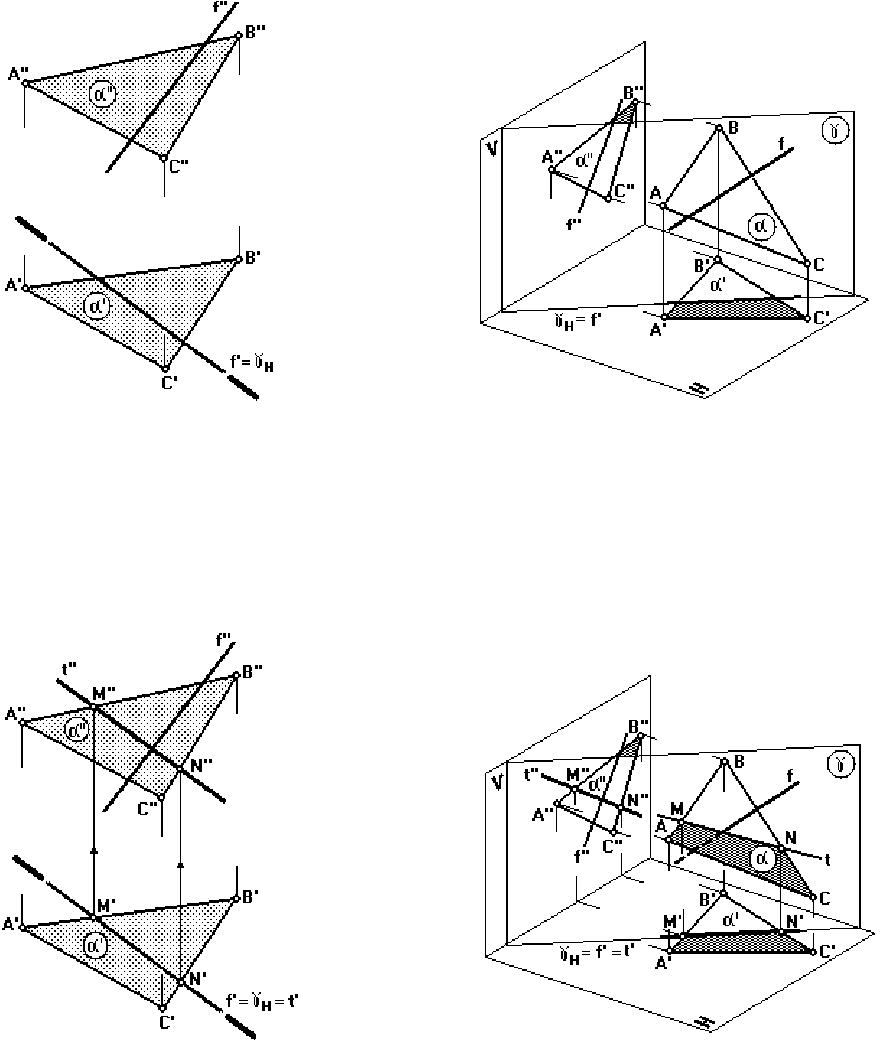
Рис. 51

Рис. 52

Проведем через прямую f вспомогательную горизонтально-проецирующую плос-

кость . Ввиду собирательного свойства проецирующих плоскостей горизонтальный след

этой плоскости совпадет с горизонтальной проекцией прямой f (f').

2 этап (рис. 53, 54)

Находим линию пересечения двух плоскостей: данной (ABC) и вспомогательной

γ – прямую t.

По горизонтальной проекции t' определяем фронтальную проекцию t''.

Рис. 53

Рис. 54

3 этап (рис. 55, 56)

Определяем точку пересечения найденной линии пересечения плоскостей t с дан-

ной прямой f.

Рис. 55

Рис. 56

Сначала на пересечении фронтальных проекций прямых f и t (f''× t'') определяем

фронтальную проекцию точки их пересечения K''.

Затем по линии связи находим ее горизонтальную проекцию K'.

Точка K, принадлежащая как плоскости α (АВС), так и плоскости γ, будет искомой

точкой встречи прямой f с плоскостью α.

10.3. Условие видимости на чертеже

Для большей наглядности невидимые части предмета вычерчивают штриховыми

линиями (либо совсем не вычерчивают).

Вопрос о видимости решают путем сравнения координат Y или Z точек, лежащих

на одном проецирующем луче.

Точки, лежащие на одном проецирующем луче, называются

КОНКУРИРУЮЩИМИ.

Принято считать, что из двух конкурирующих точек на горизонтальной проекции

видна та точка, координата Z

которой больше, а на фронтальной проекции – координата Y

которой больше.

Из рис. 57 легко установить, что на горизонтальной проекции из двух точек С и D

видимой будет точка C (C'), а на фронтальной проекции из двух точек A и B будет види-

мой точка B (B'').

Рис. 57

Определим видимость на рис.55.

а) Для определения видимости прямой f на ГОРИЗОНТАЛЬНОЙ проекции рас-

смотрим две произвольные конкурирующие точки, например точки 1' и М' (точка 1 при-

надлежит прямой f, а точка М – отрезку АВ) (рис. 58).

Координата Z точки М больше, следовательно на горизонтальной проекции прямая

f на участке от точки 1 до точки К расположена ниже плоскости α и является невидимой

(рис.59).

Рис. 58

Рис. 59

б) Для определения видимости прямой f на ФРОНТАЛЬНОЙ проекции рассмотрим

две другие конкурирующие точки, например точки 2'' и Е'' (точка 2 принадлежит прямой f,

а точка Е – отрезку АВ) (рис. 60).

Координата Y точки 2 больше, следовательно на фронтальной проекции прямая f на

участке от точки K до точки 2 расположена перед плоскостью и является видимой (рис

61).

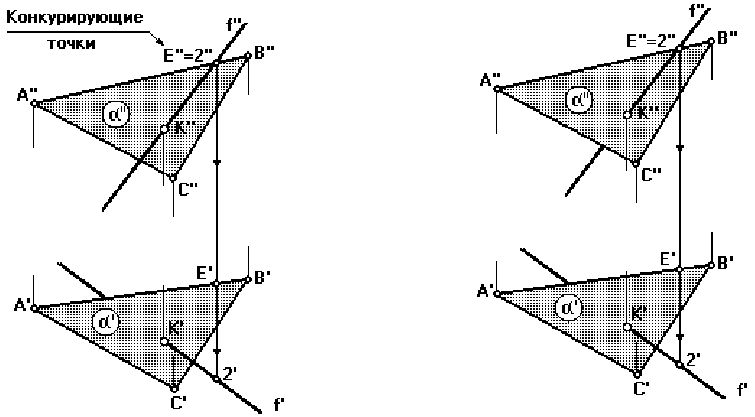
Рис. 60

Рис. 61