Васильев А., Михайлин В. Введение в спектроскопию диэлектриков

Подождите немного. Документ загружается.

drWr Wrt

rdr R r R r

()exp[ ()]

( ) exp[ ( )

−=

=−

∫

−

∞

πτ

()]t τ

=−=

∞

∫

dx tx

exp( )

()

(20.24)

Ïðàâàÿ ÷àñòü óðàâíåíèÿ (20.23) ðàâíà ñêîðîñòè óìåíüøåíèÿ êîíöåí-

òðàöèè âîçáóæäåííûõ äîíîðîâ. Èç ñîîòíîøåíèÿ (20.24) ëåãêî âè-

äåòü, ÷òî äëÿ ìàëûõ

t → 0

ýòà ñêîðîñòü ñòàíîâèòñÿ áåñêîíå÷íîé. Òà-

êîé ðåçóëüòàò ïîëó÷àåòñÿ â êîíòèíóàëüíîé ìîäåëè, êîãäà äîíîð è àê-

öåïòîð ìîãóò íàõîäèòüñÿ äðóã îò äðóãà íà ïðîèçâîëüíî ìàëîì ðàññòî-

ÿíèè. Òåì íå ìåíåå, îáëàñòü ïðèìåíèìîñòè ïðèáëèæåíèÿ (20.24) äî-

ñòàòî÷íî øèðîêàÿ, ïîñêîëüêó

Ïîñëå èíòåãðèðîâàíèÿ óðàâíåíèÿ (20.23) ñ èñïîëüçîâàíèåì

(20.24) ìîæíî ïîëó÷èòü

ntn

qn R

(;) (;)exp110

=−−













ττ

. (20.25)

Çäåñü êîíñòàíòà

ðàâíà

4374

π≈,

. Åñëè èçìåíèòü ìîäåëü äèïîëü-

äèïîëüíîãî ïåðåíîñà (íàïðèìåð, ó÷åñòü óãëîâóþ çàâèñèìîñòü âåðîÿò-

íîñòè ïåðåíîñà), çíà÷åíèå ýòîé êîíñòàíòû ìîæåò ñëåãêà îòëè÷àòüñÿ

îò ïðèâåäåííîãî âûøå.

Ïîêàçàòåëü ñòåïåíè

12 36=

â ýêñïîíåíòå çàìåíÿåòñÿ íà

äëÿ

äèïîëü-êâàäðóïîëüíîãî ïåðåíîñà è íà

310

äëÿ êâàäðóïîëü-êâàäðóïî-

ëüíîãî. Åñëè âåðîÿòíîñòü ïåðåíîñà çàâèñèò îò ðàññòîÿíèÿ ýêñïîíåí-

öèàëüíî,

Wr rR()~exp( )−

, ÷òî ïðîèñõîäèò, íàïðèìåð, äëÿ òóííå-

ëüíîãî ïåðåíîñà, ñêîðîñòü ðàñïàäà èìååò ëîãàðèôìè÷åñêóþ îñîáåí-

íîñòü. Òåì ñàìûì òóííåëüíûé ðàñïàä ïîä÷èíÿåòñÿ ñòåïåííîìó çàêî-

íó (

nt~

−ρ

Íåýêñïîíåíöèàëüíûé ðàñïàä (20.25) ìîæíî îáúÿñíèòü ñëåäóþ-

ùèì îáðàçîì. Íà ñàìûõ íà÷àëüíûõ ñòàäèÿõ ðàñïàäà ïåðåíîñ ïðîèñ-

õîäèò íà áëèæàéøèõ ïàðàõ. Êîíöåíòðàöèÿ äîíîðîâ ïàäàåò áûñòðî,

ïîñêîëüêó ñêîðîñòü ïåðåíîñà äëÿ òàêèõ ïàð âûñîêà. Äëÿ ïîñëåäóþ-

ùèõ ñòàäèé ðåëàêñàöèè áëèçêèå ïàðû óæå îòñóòñòâóþò, è ïåðåíîñ

îïðåäåëÿåòñÿ ïàðàìè ñ áîëüøèì ðàññòîÿíèåì ìåæäó íèìè. Íà ïî-

ñëåäíèõ ñòàäèÿõ ðåëàêñàöèè îïðåäåëÿþùèì îñòàåòñÿ òîëüêî ðàäèà-

öèîííûé ðàñïàä. Îäíàêî, ñêîðîñòü ðàñïàäà (20.24) óìåíüøàåòñÿ äî-

ñòàòî÷íî ìåäëåííî, è ïåðåíîñ íàáëþäàåòñÿ â êèíåòèêå äàæå íà äàëå-

êèõ ñòàäèÿõ ðåëàêñàöèè.

262 Ãëàâà 4. Âòîðè÷íûå ïðîöåññû

§21 Ðåàáñîðáöèÿ ëþìèíåñöåíöèè

Â ïðåäûäóùåì ïàðàãðàôå îáñóæäàëñÿ ïåðåíîñ ýíåðãèè, âîçíèêà-

þùèé èç-çà îáìåíà âèðòóàëüíûìè ïðîäîëüíûìè ôîòîíàìè. Ýëåêòðè-

÷åñêîå ïîëå òàêèõ ôîòîíîâ ïàäàåò ñ ðàññòîÿíèåì êàê

−3

. Ïîýòîìó

òàêîå âçàèìîäåéñòâèå âàæíî òîëüêî â òîì ñëó÷àå, êîãäà ðàññòîÿíèå

ìåæäó âîçáóæäåííûì öåíòðîì è öåíòðîì, ïðèíèìàþùèì ýíåðãèþ,

äîñòàòî÷íî ìàëî. Èìååòñÿ äðóãàÿ êîìïîíåíòà ýëåêòðè÷åñêîãî ïîëÿ,

êîòîðàÿ ïàäàåò çíà÷èòåëüíî ìåäëåííåå, êàê

−1

(ñì. óðàâíåíèå

(1.8)). Ýòî ïîïåðå÷íîå ýëåêòðè÷åñêîå ïîëå èçëó÷åíèÿ.

Òåîðèÿ òàêîãî ïåðåíîñà ìîæåò áûòü ðàññìîòðåíà ñîâåðøåííî

àíàëîãè÷íî äèïîëü-äèïîëüíîìó ïåðåíîñó, åñëè âìåñòî âûðàæåíèÿ

äëÿ

()K

(20.1) èñïîëüçîâàòü âûðàæåíèå (ñì. (1.8)):

()

() ()

rrr

ij i j

in rc rc

r =

−

−−

ωω κωω

Òåì ñàìûì âåðîÿòíîñòü ðåàáñîðáöèè (ïîãëîùåíèÿ èñïóùåííîãî ïî-

ïåðå÷íîãî ôîòîíà) ðàâíà

lum

→

−

ωω

αω

()

∫

abs

().ω

Çäåñü êîýôôèöèåíò óãëîâîãî ðàñïðåäåëåíèÿ

äëÿ ñëó÷àéíûõ íà-

ïðàâëåíèé äèïîëüíûõ ìîìåíòîâ ðàâåí

. Âîñïîëüçîâàâøèñü óðàâ-

íåíèÿìè (20.5) è (20.6), ýòî âûðàæåíèå ìîæíî ïåðåïèñàòü â âèäå

Ied

→

−

∫

πτ

ωα ω ω

αω

() () .

()

Åñëè àêöåïòîðû ðàñïðåäåëåíû ðàâíîìåðíî ñ êîíöåíòðàöèåé

ïîëíàÿ ñêîðîñòü ðàñïàäà ìîæåò áûòü âû÷èñëåíà ïóòåì èíòåãðèðîâà-

íèÿ (20.1) ïî âñåìó ïðîñòðàíñòâó:

πnRdRW R

→

∞

∫

=()

∫∫

−

∞

ωωαω

αω

dI e dR

() ()

()

∫

−

ωωτ

()

, (21.2)

ãäå ìû èñïîëüçîâàëè ïðåäïîëîæåíèå î ñëó÷àéíîì ðàñïðåäåëåíèè íà-

ïðàâëåíèé äèïîëüíîãî ìîìåíòà. Ïîãëîùåíèå ïðåäïîëàãàåòñÿ ñâÿçàí-

íûì òîëüêî ñ ïîãëîùåíèåì àêöåïòîðîâ (

αω α ω() ()=

). Ñîîòíîøåíèå

(21.2) èìååò î÷åâèäíûé ñìûñë: êàæäûé ïîïåðå÷íûé ôîòîí, êîòîðûé

èñïóñêàåòñÿ âîçáóæäåííûì öåíòðîì, áóäåò ãäå-íèáóäü ïîãëîùåí.

Òåì ñàìûì ñêîðîñòü ðàäèàöèîííîãî ïåðåíîñà ðàâíà îáðàòíîìó ðàäèà-

öèîííîìó âðåìåíè.

Ðåàáñîðáöèÿ èçëó÷åíèÿ èãðàåò âàæíóþ ðîëü â ïåðåíîñå ýíåðãèè

íà áîëüøèå ðàññòîÿíèÿ. Â êà÷åñòâå ïðèìåðà ðàññìîòðèì ñòàöèîíàð-

íûé ñëó÷àé, êîãäà ðàñïðåäåëåíèå öåíòðîâ îáîèõ òèïîâ îäíîðîäíî, à

âîçáóæäåíèå íåîäíîðîäíî. Ïðåäïîëîæèì, ÷òî èíòåíñèâíîñòü âîç-

áóæäåíèÿ ðàâíà

I()r

. Êîíöåíòðàöèÿ âîçáóæäåííûõ öåíòðîâ òàêæå çà-

âèñèò îò êîîðäèíàò:

() (,)11= r

(îáîçíà÷åíèÿ àíàëîãè÷íû èñïî-

ëüçîâàííûì â ðàçäåëå 20.2). Êèíåòè÷åñêîå óðàâíåíèå ìîæåò áûòü çà-

ïèñàíî â âèäå

In n

nW n

() (,) (,) ,

(,) ( )

rr r

rrr

ατ

110

−=

−′

−

→

∫

(,) (,) .′′− =

−

rr110

dr nτ

Åñëè ïðåäïîëîæèòü, ÷òî èíòåíñèâíîñòü âîçáóæäåíèÿ íå ñëèøêîì âû-

ñîêà, ìîæíî çàïèñàòü

αα

(,)r 0

. Òîãäà êîíöåíòðàöèÿ âîçáóæäåí-

íûõ àêöåïòîðîâ ðàâíà

nnnWIdr

dd da

(,) ( ) ( ) .rrrr1

000 3

=−′′′

→

∫

ττ α

(21.3)

Òàêèì îáðàçîì, îíà ïðîïîðöèîíàëüíà òðåõìåðíîé ñâåðòêå èí-

òåíñèâíîñòè âîçáóæäàþùåãî èçëó÷åíèÿ è âåðîÿòíîñòè ðàäèàöèîííî-

ãî ïåðåíîñà.

Åñëè âîçáóæäàþùèé ñâåò ïàäàåò íà ïîëóáåñêîíå÷íîå òâåðäîå

òåëî, è èíòåíñèâíîñòü ñâåòà íå çàâèñèò îò êîîðäèíàò â ïëîñêîñòè, ïà-

ðàëëåëüíîé ïîâåðõíîñòè, çàäà÷à ñòàíîâèòñÿ îäíîìåðíîé. Âñå êîí-

öåíòðàöèè òåïåðü ñòàíîâÿòñÿ ôóíêöèÿìè òîëüêî îäíîé êîîðäèíàòû

. Óðàâíåíèå (21.3) ìîæåò áûòü çàïèñàíî â ôîðìå (Àãðàíîâè÷, Ãàëà-

íèí, 1978)

n x dx Q x x I x

(,) ( )( ),1 =′−′′

∫

ãäå ÿäðî

Qx()

îïðåäåëÿåòñÿ èíòåãðàëîì

264 Ãëàâà 4. Âòîðè÷íûå ïðîöåññû

Q x n n W x y z dy dz

() (,,)==

→

∫

ττ α

dd da

000

⊥

−+

∫∫

τα

ωωαω

αω

() ()

()

−

∞

∫∫

τα

ωωαω

αω

() ()

()

()[]

=−−

∫

τα

ωωαω αω

dI x

() () () .

Çäåñü

Ei( )x e dt t

−∞

∫

(21.4)

—èíòåãðàëüíàÿ ýêñïîíåíòà. Àñèìïòîòè÷åñêîå ïîâåäåíèå

Ei( )−x

èìååò

âèä

−−= →∞

−−=−+ → =

−

Ei C C

() , ,

( ) ln( ), , ,

xexx

xxx

1 0 0 577215K

Åñëè èíòåíñèâíîñòü âîçáóæäàþùåãî ñâåòà ïàäàåò ïðè ïðîõîæäå-

íèè âãëóáü êðèñòàëëà êàê

Ix I e

() ,

()

−

αω

ãäå

— ÷àñòîòà âîçáóæäàþùåãî ñâåòà,

αω α()

= n

— ïîòîê

ôîòîíîâ, ïàäàþùèõ íà ïîâåðõíîñòü êðèñòàëëà, êîíöåíòðàöèÿ âîç-

áóæäåííûõ àêöåïòîðîâ îêàçûâàåòñÿ ðàâíîé

()

dI x

Ei(,) () () ()1

=−−+







∫

ωωαω αω

()+−−+

−

xαω

αω αω

()

() ( ) ln

() ( )







Ïîëíîå ÷èñëî âîçáóæäåííûõ àêöåïòîðîâ ðàâíî

Nnxdx

() ( , )11

∞

∫

§21. Ðåàáñîðáöèÿ ëþìèíåñöåíöèè 265

=++























ωω

αω

11()

()



∫

Ïîñêîëüêó ìû íå ó÷èòûâàåì íèêàêîãî òóøåíèÿ ëþìèíåñöåíöèè, èí-

òåíñèâíîñòü ëþìèíåñöåíöèè äîíîðîâ ðàâíà

1−

()τ

. Òåì ñà-

ìûì êâàíòîâûé âûõîä ëþìèíåñöåíöèè äîíîðîâ ðàâåí òîé ÷àñòè ëþ-

ìèíåñöåíöèè, êîòîðàÿ íå ïåðåïîãëîùàåòñÿ êðèñòàëëîì:

ηωω

αω

=−+

























11dI()

()

∫

. (21.5)

Åñëè êîýôôèöèåíò ïîãëîùåíèÿ äëÿ ñâåòà ëþìèíåñöåíöèè ìíîãî ìå-

íüøå, ÷åì äëÿ âîçáóæäàþùåãî ñâåòà (íàïðèìåð, åñëè ëþìèíåñöåí-

öèÿ âîçáóæäàåòñÿ â îáëàñòè ôóíäàìåíòàëüíîãî ïîãëîùåíèÿ, à èçëó-

÷åíèå ïîïàäàåò â îáëàñòü ïðîçðà÷íîñòè êðèñòàëëà), êâàíòîâûé âû-

õîä ñòàíîâèòñÿ ðàâíûì

, ïîñêîëüêó òîëüêî ïîëîâèíà ôîòîíîâ èñ-

ïóñêàþòñÿ â íàïðàâëåíèè ê ïîâåðõíîñòè (çäåñü ìû íå ó÷èòûâàåì êîð-

ðåêòèðóþùèé ìíîæèòåëü (16.2), âîçíèêàþùèé èç-çà ïîëíîãî âíóò-

ðåííåãî îòðàæåíèÿ). Â ïðîòèâîïîëîæíîì ñëó÷àå, êîãäà ëþìèíåñöåí-

öèÿ ñèëüíî ïîãëîùàåòñÿ (íàïðèìåð, â ñëó÷àå æåñòêîãî ðåíòãåíîâñêî-

ãî âîçáóæäåíèÿ è äîñòàòî÷íî ìÿãêîé ðåíòãåíîâñêîé ôëþîðåñöåíöèè)

êâàíòîâûé âûõîä îêàçûâàåòñÿ ðàâíûì

ηωω

αω

∫

dI()

()

(21.6)

è ìíîãî ìåíüøå åäèíèöû.

Åñëè ðåàáñîðáöèÿ ÿâëÿåòñÿ ñèëüíîé, ñïåêòð ëþìèíåñöåíöèè äî-

íîðà èçìåíÿåòñÿ (ñïåêòð ïðîïîðöèîíàëåí ïîäûíòåãðàëüíûì âûðàæå-

íèÿì â ñîîòíîøåíèÿõ (21.5) è (21.6)). Ïîñêîëüêó ýòî ïîäûíòåãðàëü-

íîå âûðàæåíèå â îáùåì ñëó÷àå çàâèñèò îò ãëóáèíû ïðîíèêíîâåíèÿ

αω

−1

()

âîçáóæäàþùåãî ñâåòà, íàáëþäàåìûé ñïåêòð òàêîé ëþìèíåñ-

öåíöèè òàêæå çàâèñèò îò ýòîé âåëè÷èíû. Íàèáîëåå ÿâíûì ïðèìåðîì

ÿâëÿåòñÿ ñðàâíåíèå âîçáóæäåíèÿ îäíîãî è òîãî æå öåíòðà ñ ïîìîùüþ

ÂÓÔ-ôîòîíîâ è ñ ïîìîùüþ ðåíòãåíîâñêèõ ôîòîíîâ. Ðåàáñîðáöèÿ

ëþìèíåñöåíöèè â ñëó÷àå ðåíòãåíîâñêèõ ôîòîíîâ ïðîÿâëÿåòñÿ çíà÷è-

òåëüíî ñèëüíåå, ïîñêîëüêó ãëóáèíà ïðîíèêíîâåíèÿ ðåíòãåíîâñêîãî

èçëó÷åíèÿ íàìíîãî áîëüøå.

Ñðàâíåíèå ñëó÷àåâ ðåàáñîðáöèè ëþìèíåñöåíöèè è äèïîëü-äèïî-

ëüíîãî ïåðåíîñà ïîêàçûâàåò, ÷òî â ïîñëåäíåì ñëó÷àå íå ïðîèñõîäèò

èçìåíåíèÿ ñïåêòðà ñâå÷åíèÿ, à íàáëþäàåòñÿ òîëüêî òóøåíèå èíòåí-

ñèâíîñòè ëþìèíåñöåíöèè.

Âûøå ìû ðàññìàòðèâàëè òîëüêî ïîëóïðîñòðàíñòâî, çàíèìàåìîå

òâåðäûì òåëîì. Ìîæíî ðàññìîòðåòü òàêæå ñëó÷àè ðåàáñîðáöèè â ïëà-

ñòèíå è äëÿ äðóãèõ ãåîìåòðèé. Çäåñü ìû ïîä÷åðêíåì, ÷òî â ñëó÷àå

266 Ãëàâà 4. Âòîðè÷íûå ïðîöåññû

ñèëüíîé ðåàáñîðáöèè ñïåêòð ñâå÷åíèÿ, èçìåðÿåìûé ñ ïåðåäíåé ïî-

âåðõíîñòè êðèñòàëëà (íà êîòîðóþ ïàäàåò èçëó÷åíèå) îòëè÷àåòñÿ îò

ñïåêòðà ñâå÷åíèÿ, èçìåðÿåìîãî ñ çàäíåé ïîâåðõíîñòè, ïîñêîëüêó â

ïîñëåäíåì ñëó÷àå ñâåò ïðîõîäèò áîëüøèé ïóòü è ïåðåïîãëîùåíèå ñè-

ëüíåå âèäîèçìåíÿåò ñïåêòð.

Çäåñü ìû òàêæå ïðåíåáðåãàëè îáðàòíûì ïðîöåññîì, ïîëîæèâ âå-

ðîÿòíîñòü

ad→

ðàâíîé íóëþ. Òåì ñàìûì âûïàë èç ðàññìîòðåíèÿ

ñëó÷àé ñàìîïîãëîùåíèÿ, êîãäà ðåàáñîðáöèÿ ïðîèñõîäèò íà öåíòðàõ

òîãî æå òèïà. Åñëè ýòà âåðîÿòíîñòü îòëè÷íà îò íóëÿ, ìîæåò ïðîèñõî-

äèòü ìíîãîêðàòíîå ïåðåïîãëîùåíèå. Ýòî ïðèâîäèò íå òîëüêî ê èçìå-

íåíèÿì ñïåêòðà ëþìèíåñöåíöèè, íî è ê ìîäèôèêàöèè êèíåòèêè ëþ-

ìèíåñöåíöèè. Êèíåòèêà ñòàíîâèòñÿ íåýêñïîíåíöèàëüíîé è áîëåå ìåä-

ëåííîé, ÷åì áåç ó÷åòà ïåðåïîãëîùåíèÿ. Êèíåòèêà çàâèñèò îò âåðîÿò-

íîñòè âûõîäà êâàíòà ëþìèíåñöåíöèè èç êðèñòàëëà è òåì ñàìûì îïðå-

äåëÿåòñÿ ãåîìåòðèåé ñèñòåìû. Ðàçëè÷íûå ðåçóëüòàòû òàêîãî ðîäà

ïðèâåäåíû â ìîíîãðàôèè Àãðàíîâè÷à è Ãàëàíèíà (1978).

§21. Ðåàáñîðáöèÿ ëþìèíåñöåíöèè 267

§22 Ìîäåëü îäíîðîäíîãî âîçáóæäåíèÿ êðèñòàëëà

22.1 Âîçáóæäåíèå äåôåêòîâ â ïðè íàëè÷èè ëîâóøåê

Ðàññìîòðèì áîëåå ïîäðîáíî ïðè÷èíû, áëàãîäàðÿ êîòîðûì âòî-

ðè÷íûå ïðîöåññû â êðèñòàëëàõ ñòàíîâÿòñÿ íåëèíåéíûìè è èíåðöèîí-

íûìè. Îáà ýòèõ ñâîéñòâà íà÷èíàþò ïðîÿâëÿòüñÿ, êàê òîëüêî êâàíòû

âîçáóæäàþùåãî èçëó÷åíèÿ ïðèîáðåòàþò ýíåðãèþ, äîñòàòî÷íóþ äëÿ

èîíèçàöèè öåíòðîâ ñâå÷åíèÿ. Ïðè áîëüøèõ ýíåðãèÿõ íåëèíåéíîñòü è

èíåðöèîííîñòü ñîõðàíÿþòñÿ. Â òî æå âðåìÿ, åñëè ýíåðãèè ôîòîíîâ

õâàòàåò ëèøü íà âîçáóæäåíèå

öåíòðîâ ñâå÷åíèÿ, à íå íà èõ

èîíèçàöèþ, íåëèíåéíîñòü ïåðå-

ñòàåò ïðîÿâëÿòüñÿ (ïðè äîñòà-

òî÷íî ñëàáûõ è óìåðåííûõ èí-

òåíñèâíîñòÿõ), à ïîñëåñâå÷åíèå

îïèñûâàåòñÿ ïðîñòûìè ýêñïî-

íåíöèàëüíûì çàêîíîì çàòóõà-

íèÿ.

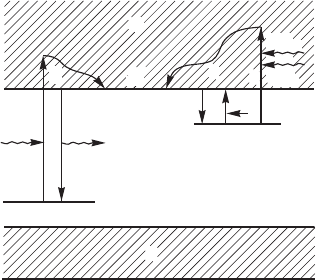
Ïðîñòåéøàÿ ìîäåëü, â êîòî-

ðîé ìîãóò ïðîèñõîäèòü íåëèíåé-

íûå è èíåðöèîííûå ÿâëåíèÿ,

èçîáðàæåíà íà ðèñ. 51. Âîçáóæ-

äàþùåå èçëó÷åíèå ñ ýíåðãèåé

ôîòîíîâ

hν

èîíèçèðóåò öåíòðû

ñâå÷åíèÿ (ïðîöåññ 1). Â §19

áûëî ïîêàçàíî, ÷òî çàõâàò íà ëî-

âóøêè è öåíòðû ñâå÷åíèÿ èç ãîðÿ÷åãî ñîñòîÿíèÿ ýëåêòðîíà èìååò ãî-

ðàçäî ìåíüøóþ âåðîÿòíîñòü, ÷åì çàõâàò èç òåðìàëèçîâàííîãî ñîñòîÿ-

íèÿ, ïîñêîëüêó òåðìàëèçîâàííûé ýëåêòðîí èìååò ñóùåñòâåííî ìåíü-

øóþ ñêîðîñòü, à çàõâàò ïðîèñõîäèò áåç àêòèâàöèîííîãî áàðüåðà. Ïî-

ýòîìó ãîðÿ÷èé ýëåêòðîí áûñòðî (çà âðåìÿ

10 10

13 12−−

ñ) òåðìàëèçó-

åòñÿ (3). Îñîáåííî áûñòðî ýòîò ïðîöåññ ïðîòåêàåò â èîííûõ êðèñòàë-

ëàõ, ãäå ýëåêòðîíû èíòåíñèâíî âçàèìîäåéñòâóþò ñ ïðîäîëüíûìè îï-

òè÷åñêèìè ôîíîíàìè, ñâÿçàííûìè ñ ïîëÿðèçàöèåé êðèñòàëëà. Ïîñëå

òåðìàëèçàöèè ó ýëåêòðîíà åñòü äâå âîçìîæíîñòè: îí ìîæåò áûòü çà-

õâà÷åí ëèáî öåíòðîì ñâå÷åíèÿ ñ èñïóñêàíèåì ôîòîíà ëþìèíåñöåíöèè

(ïðîöåññ 2), ëèáî íà ëîâóøêîé ýëåêòðîíîâ (4). Âûñâå÷èâàíèå öåíòðà

lum

Ðèñ. 51. Ñõåìà ïðîöåññîâ ïðè èîíè-

çàöèè äåôåêòà â ïðèñóòñòâèè ëîâó-

ñâå÷åíèÿ ñ èñïóñêàíèåì ôîòîíà

hν

lum

ìîæåò ïðîèñõîäèòü ïðè ïåðå-

õîäå èç çîíû ïðîâîäèìîñòè íà îñíîâíîé óðîâåíü, èëè (÷òî áîëåå âå-

ðîÿòíî) ìîæåò îñóùåñòâëÿòüñÿ ÷åðåç ïðîìåæóòî÷íîå îáðàçîâàíèå

âîçáóæäåííîãî ñîñòîÿíèÿ. Çà ñ÷åò ðåëàêñàöèè îêðóæåíèÿ öåíòðà ñâå-

÷åíèÿ è â ñîãëàñèè ñ ïðèíöèïîì Ôðàíêà-Êîíäîíà ýíåðãèÿ êâàíòà ñâå-

÷åíèÿ ìîæåò áûòü çíà÷èòåëüíî ìåíüøå ïîðîãà èîíèçàöèè öåíòðà.

Ýëåêòðîíû, çàõâà÷åííûå íà ëîâóøêè, ìîãóò äîâîëüíî äîëãî íà-

õîäèòüñÿ íà íèõ. Äëÿ âûñâîáîæäåíèÿ ýëåêòðîíîâ ñ ëîâóøåê åñòü äâà

ïóòè. Âî-ïåðâûõ, ýòî òåðìè÷åñêîå îñâîáîæäåíèå ýëåêòðîíîâ ñ ïîãëî-

ùåíèåì ôîíîíîâ (5). Âî-âòîðûõ, ëîâóøêè ìîãóò èîíèçîâàòüñÿ (6)

ïîä äåéñòâèåì âîçáóæäàþùåãî èçëó÷åíèÿ (

hν

) èëè äðóãîãî ýëåêò-

ðîìàãíèòíîãî èçëó÷åíèÿ ìåíüøåé ýíåðãèè (

hν

). Òàêèì èçëó÷åíèåì

ìîãóò ñïåöèàëüíî ïîäñâå÷èâàòü îáðàçåö äëÿ âûïîëíåíèÿ çàäà÷, êîòî-

ðûå îáñóæäàþòñÿ íèæå. Âûñâîáîæäàþùèåñÿ ýëåêòðîíû çàòåì áûñò-

ðî òåðìàëèçóþòñÿ (7) è çàõâàòûâàþòñÿ öåíòðàìè è ëîâóøêàìè.

Ðàññìîòðèì ïîñëåäîâàòåëüíî âåðîÿòíîñòè êàæäîãî èç ýòèõ ïðî-

öåññîâ. Ïðè ýòîì áóäåì ïðåäïîëàãàòü, ÷òî âîçáóæäåíèå îáðàçöà îä-

íîðîäíî, ïîýòîìó ìîæíî ââåñòè êîíöåíòðàöèè öåíòðîâ ñâå÷åíèÿ â íå-

âîçáóæäåííîì ñîñòîÿíèè

, èîíèçîâàííûõ öåíòðîâ

, ïîëíóþ êîí-

öåíòðàöèþ ëîâóøåê

è êîíöåíòðàöèþ çàõâà÷åííûõ íà ëîâóøêàõ

ýëåêòðîíîâ

, à òàêæå êîíöåíòðàöèþ ýëåêòðîíîâ â çîíå ïðîâîäèìî-

ñòè

−

. Êàê óæå áûëî ñêàçàíî, ýëåêòðîíû â ãîðÿ÷åì ñîñòîÿíèè ïðî-

âîäÿò êðàéíå ìàëîå âðåìÿ, ïîýòîìó

−

îïèñûâàåò êîíöåíòðàöèþ òåð-

ìàëèçîâàííûõ ýëåêòðîíîâ. Âåðîÿòíîñòü èîíèçàöèè ïîä äåéñòâèåì

ôîòîíîâ ïîãëîùàåìîãî èçëó÷åíèÿ ïðîïîðöèîíàëüíà ÷èñëó íåèîíèçî-

âàííûõ öåíòðîâ (

−

), èíòåíñèâíîñòè ïàäàþùåãî íà îáðàçåö ñâåòà

It()

è ñå÷åíèÿ ïîãëîùåíèÿ íà îäíîì öåíòðå

wnnIt

=−α ()()

(ñðàâíèòå ñ ïîñëåäíèì ÷ëåíîì ïåðâîãî óðàâíåíèÿ ñèñòåìû (20.20)).

Âåðîÿòíîñòü çàõâàòà ñ èçëó÷åíèåì ôîòîíà ëþìèíåñöåíöèè ïðîïîð-

öèîíàëüíà â ïðîñòåéøåì ïðèáëèæåíèè êàê ÷èñëó ýëåêòðîíîâ â çîíå

ïðîâîäèìîñòè, òàê è èîíèçîâàííûõ öåíòðîâ (ñì. óðàâíåíèå (19.8)):

wnN

−

Àíàëîãè÷íî ìîæíî ïîëó÷èòü âåðîÿòíîñòè äëÿ îñòàëüíûõ ïðîöåññîâ:

wNNN

=−

−

γ ()

=ω

wNI

=δ

Çäåñü

— êîýôôèöèåíòû ïðîïîðöèîíàëüíîñòè, à

—

èíòåíñèâíîñòü âûñâå÷èâàþùåãî ñâåòà (åñëè íåò äîïîëíèòåëüíîé ïîä-

ñâåòêè,

ñîâïàäàåò ñ

). Çíàÿ âñå ýòè âåðîÿòíîñòè, ìîæíî çàïèñàòü

óðàâíåíèÿ áàëàíñà äëÿ ÷èñëà èîíèçîâàííûõ öåíòðîâ è ýëåêòðîíîâ,

§22. Ìîäåëü îäíîðîäíîãî âîçáóæäåíèÿ êðèñòàëëà 269

çàõâà÷åííûõ íà ëîâóøêàõ, òî åñòü êèíåòè÷åñêèå óðàâíåíèÿ äëÿ ëþ-

ìèíåñöèðóþùåãî êðèñòàëëà:

dn dt w w n n I n N=−= − −

−

αβ()

dN dt w w w N N N N N I

=−−= − − −

−

456 0 1

γωδ()

dN dt w w w w w

−

=++−−

15624

. (22.1)

Ïîñëåäíåå óðàâíåíèå ìîæíî ïîëó÷èòü èç óñëîâèÿ íåéòðàëüíîñòè îá-

ðàçöà, ïî êîòîðîìó ÷èñëî èîíèçîâàííûõ öåíòðîâ ñîâïàäàåò ñ ñóììîé

÷èñåë ýëåêòðîíîâ â çîíå è íà ëîâóøêàõ:

nNN=+

−

Ââåäåì óïðîùàþùèå ïðåäïîëîæåíèÿ î êîíöåíòðàöèè ýëåêòðî-

íîâ. Âî-ïåðâûõ, ïðè íå î÷åíü âûñîêèõ èíòåíñèâíîñòÿõ

nn<<

NN<<

, ò. å. äîëÿ èîíèçîâàííûõ öåíòðîâ è çàïîëíåííûõ ëîâóøåê

ìíîãî ìåíüøå åäèíèöû. Âî-âòîðûõ, âðåìÿ æèçíè ýëåêòðîíîâ â çîíå

ïðîâîäèìîñòè ìíîãî ìåíüøå âðåìåíè èõ ïðåáûâàíèÿ íà ëîâóøêàõ. Â

òîì ñëó÷àå, êîãäà âåðîÿòíîñòü çàõâàòà íà ëîâóøêó íå ÷ðåçâû÷àéíî

ìàëà,

−

. Åñëè ââåñòè îäíîâðåìåííî è ïðåäïîëîæåíèå î ìàëî-

ñòè ïðîèçâîäíûõ

dN dt dN dt

−

, òî ñèñòåìà óðàâíåíèé (22.1) çíà-

÷èòåëüíî óïðîùàåòñÿ (èç íåéòðàëüíîñòè ñëåäóåò

nN≈

dn dt n I n N=−

−

αβ

dn dt N N n n I

=−−

−

γωδ

. (22.2)

Ýòà ñèñòåìà óðàâíåíèé è áóäåò èññëåäîâàòüñÿ.

Ðàññìîòðèì âíà÷àëå ñòàöèîíàðíûé ñëó÷àé. ×åðåç êàêîå-òî âðåìÿ

ïîñëå âêëþ÷åíèÿ ñâåòà óñòàíàâëèâàåòñÿ ðàâíîâåñíîå ñîñòîÿíèå. Âå-

ëè÷èíû, ñîîòâåòñòâóþùèå ýòîìó ñëó÷àþ, áóäóò îáîçíà÷àòüñÿ èíäåê-

ñîì

∞

. Ïðè ýòîì ñèñòåìà (22.2) ïåðåõîäèò â ñèñòåìó àëãåáðàè÷åñêèõ

óðàâíåíèé, ïîñêîëüêó

dn dt

∞

. Â çîíå ïðîâîäèìîñòè óñòàíàâëèâà-

åòñÿ ðàâíîâåñíàÿ êîíöåíòðàöèÿ ýëåêòðîíîâ:

∞

−

∞

ãäå

∞

ïîëó÷àåòñÿ èç óðàâíåíèÿ

γα

ωδ

NnI

∞

=+()

, òî åñòü

NnI

∞

γα

βω δ

()

Ïðåäïîëîæåíèå î ìàëîñòè

−

âûïîëíÿåòñÿ â òîì ñëó÷àå, åñëè

γωδNI

T01

>> +

, ò. å. âåðîÿòíîñòü âûñâîáîæäåíèÿ ýëåêòðîíà èç

270 Ãëàâà 4. Âòîðè÷íûå ïðîöåññû

îäíîé ëîâóøêè ìíîãî ìåíüøå âåðîÿòíîñòè çàõâàòà îäíîãî ýëåêòðîíà

íà ëîâóøêó. Ñâå÷åíèå îáðàçöà ñâÿçûâàåòñÿ ñ ÷ëåíîì ðåêîìáèíàöèè

íà öåíòðå ñâå÷åíèÿ, ïîýòîìó ÷èñëî èñïóùåííûõ â åäèíèöó âðåìåíè

åäèíèöåé îáúåìà êâàíòîâ ñîâïàäàåò ñ

. Â ñòàöèîíàðíîì ñëó÷àå äëÿ

äàííîé ìîäåëè áåç òóøåíèÿ ýòî ÷èñëî ñîâïàäàåò ñ ÷èñëîì êâàíòîâ,

ïîãëîùåííûõ öåíòðîì ñâå÷åíèÿ. Îäíàêî êâàíòîâûé âûõîä â òàêîé

ñèòóàöèè îòëè÷åí îò åäèíèöû, ïîñêîëüêó âîçáóæäàþùèé ñâåò ïîãëî-

ùàåòñÿ íå òîëüêî íà öåíòðàõ ñâå÷åíèÿ, íî è íà ëîâóøêàõ (÷ëåí

Åñëè íåò äîïîëíèòåëüíîé äëèííîâîëíîâîé ïîäñâåòêè, òî

. Ïîë-

íîå ÷èñëî ïîãëîùåííûõ åäèíèöåé îáúåìà êâàíòîâ ðàâíî

. Ïî-

ýòîìó êâàíòîâûé âûõîä ëþìèíåñöåíöèè îêàçûâàåòñÿ ðàâíûì

ηδ

αβωδ













−

()

Ïðè ìàëûõ èíòåíñèâíîñòÿõ êâàíòîâûé âûõîä ðàâåí åäèíèöå, ïðè áî-

ëüøèõ èíòåíñèâíîñòÿõ, êîãäà âåðîÿòíîñòü îïòè÷åñêîãî âûñâîáîæäå-

íèÿ ýëåêòðîíîâ ñ ëîâóøåê âûøå âåðîÿòíîñòè òåïëîâîãî âûñâîáîæäå-

íèÿ, êâàíòîâûé âûõîä ñòàíîâèòñÿ ìåíüøå åäèíèöû:

γδ

αβ













−

Ýòî óìåíüøåíèå êâàíòîâîãî âûõîäà îáóñëîâëåíî òàê íàçûâàåìûì

âûñâå÷èâàþùèì äåéñòâèåì âîçáóæäàþùåãî ñâåòà.

Òåìïåðàòóðíàÿ çàâèñèìîñòü êâàíòîâîãî âûõîäà îïðåäåëÿåòñÿ

íàèáîëåå ðåçêî çàâèñÿùèì îò òåìïåðàòóðû ÷ëåíîì , òî åñòü êîýôôè-

öèåíòîì òåðìîàêòèâàöèîííîãî îñâîáîæäåíèÿ ñ ëîâóøåê

. Âîîáùå

ãîâîðÿ, âñå êîýôôèöèåíòû

(,,,)αβγδ

çàâèñÿò îò òåìïåðàòóðû, îäíà-

êî ýòà çàâèñèìîñòü ÿâëÿåòñÿ îòíîñèòåëüíî ñëàáîé — ñòåïåííîé èëè

áëèçêîé ê ñòåïåííîé. Âåðîÿòíîñòü æå òåðìè÷åñêîãî îñâîáîæäåíèÿ ñ

ëîâóøêè

çàâèñèò îò îáðàòíîé òåìïåðàòóðû ýêñïîíåíöèàëüíî:

ωω

TAB

EkT≈−

exp( )

. (22.3)

Âåëè÷èíà

, íàçûâàåìàÿ ÷àñòîòíûì ôàêòîðîì, òîæå ìîæåò ñòåïåí-

íûì îáðàçîì çàâèñåòü îò òåìïåðàòóðû, îäíàêî îñíîâíàÿ çàâèñèìîñòü

îò òåìïåðàòóðû îïðåäåëÿåòñÿ ýêñïîíåíòîé. Ýíåðãèÿ àêòèâàöèè

ðàâíà òåðìè÷åñêîé ãëóáèíå ëîâóøêè. Ñ ðîñòîì òåìïåðàòóðû âåëè÷è-

íà

ðåçêî âîçðàñòàåò, è êâàíòîâûé âûõîä â íåêîòîðîé îáëàñòè èí-

òåíñèâíîñòåé ìîæåò âîçðàñòàòü.

22.2 Êèíåòèêà ïåðâîãî ïîðÿäêà

§22. Ìîäåëü îäíîðîäíîãî âîçáóæäåíèÿ êðèñòàëëà 271