Валькова Т.А. и др. Теоретическая механика

Пусть положение материальной точки массой m в инерциальной

системе отсчета задано радиус-вектором

r



(рис. 10.1). В общем случае

равнодействующая сил

R



, действующих на точку, может зависеть от

положения точки, ее скорости и времени, т. е.

) ,, ( t

dt

rd

rRR





. (10.5)

По определению

2

dt

rd

a





. (10.6)

С учетом (10.5) и (10.6) основное уравнение динамики (10.1) можно записать

в виде

) ,, (

2

t

dt

rd

rR

dt

rd

m





. (10.7)

Уравнение (10.7)

называется дифференциальным уравнением движения

материальной точки в векторной форме

.

При решении задач обычно от векторного уравнения (10.7) переходят к

скалярным дифференциальным уравнениям движения материальной точки.

Для этого проецируют векторное уравнение (10.7) на оси выбранной системы

координат. В проекциях на декартовые оси уравнение (10.7) имеет вид

; ; ,

xyz

mx R my R mz R

&&&&

&&

(10.8)

где

, ,

x

yz

&&&&

&&

и

, ,

x

yz

RRR

 проекции ускорения точки и равнодействующей

сил, действующих на точку, соответственно на оси

х, у, z. С учетом (10.4)

возможна другая запись уравнений (10.8):

1 к 11

; ; .

nnn

кх ку кz

кк

mx F my F mz F





&&&&

&&

(10.9)

Уравнения (10.8), (10.9) называются

дифференциальными уравнениями

движения материальной точки в декартовых координатах.

При криволинейном движении материальной точки удобно поль-

зоваться системой осей естественного трехгранника: касательной

τ

, главной

нормалью

n

и бинормалью

b

. Проецируя уравнение (10.4) на эти оси, полу-

чим

τ

111

; ; ,

nnn

к n кnbкb

ккк

ma F ma F ma F







(10.10)

где

τ

, ,

nb

aaa

 соответственно касательное, нормальное и бинормальное ус-

корения точки;

τ

, ,

ккn кb

FFF

 проекции к-й силы, действующей на точку, на

касательную, главную нормаль и бинормаль.

Из кинематики известно, что

2

τ

, , 0 ,

ρ

nb

dV V

a a a

dt



(10.11)

где

Vs

&

 величина скорости точки; s  криволинейная координата;

ρ

 ра-

диус кривизны траектории точки в данный момент времени.

Подставив (10.11) в (10.10), получим

2

111

; ; 0 .

ρ

nnn

ккn кb

ккк

dV V

mFmF F

dt







(10.12)

Уравнения (10.12) являются дифференциальными уравнениями движе-

ния точки в системе естественных осей и называются

естественными урав-

нениями движения.

Ими удобно пользоваться для определения неизвестных

реакций связей в случае криволинейного движения точки.

Две задачи динамики точки

Рассматривая движение материальной точки под действием сил, дина-

мика ставит целью решение двух основных задач.

Первая задача динамики заключается в определении силы по

известному закону движения точки.

Для нахождения модуля и направления силы

F



(равнодействующей

R



), действующей на материальную точку, необходимо определить проекции

этой силы на оси декартовой системы координат или на оси естественного

трехгранника (в зависимости от способа задания движения точки). Согласно

уравнениям (10.8) и (10.12), эта задача сводится к нахождению проекций

ускорения точки, которые определяются дифференцированием по времени

соответствующих функций.

Пусть движение точки массой m задано координатным способом, т. е.

известны зависимости координат точки от времени:

( ) ; ( ) ; ( )

x

xt y yt z zt

. (10.13)

Для определения силы

F



, под действием которой происходит движе-

ние, следует:

1) найти проекции ускорения точки на декартовые оси, продиффе-

ренцировав дважды по времени уравнения движения (10.13):

xyz

a x, a y, a z





&&&&

&&

; (10.14)

2) вычислить по формулам (10.8) проекции силы

F



на оси координат:

, , ;

xyz

F

mx F my F mz

&&&&

&&

(10.15)

3) найти модуль силы

F



:

222 222

xyz

F

FFF mx

y

z 

&&&&

&&

. (10.16)

Направление силы

F



определяется с помощью направляющих косинусов:

 



ˆˆˆ

cos ; cos ; cos .

y

x

z

F

Fi Fj Fk

F

FF

 

r

rrr

rr

При естественном способе задания движения, когда известна

траектория точки и зависимость криволинейной координаты от времени,

() ,

s

st



(10.17)

для определения силы

F



, под действием которой происходит движение,

следует

1) найти по формулам (10.11) касательное и нормальное ускорения

точки, вычислив соответствующие производные по времени от закона

движения (10.17):

2

τ

, ;

ρρ

2

n

dV V s

as a

dt

  

&

&&

2) согласно (10.12) определить проекции силы

F



на оси естественного

трехгранника:

2

τ

, , 0 ;

ρ

nb

s

Fms Fm F 

&

&&

(10.18)

3) вычислить модуль силы

F



по формуле

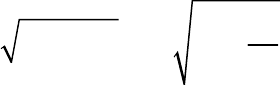
4

22 2

2

.

ρ

n

s

FFFms



 

&

&&

(10.19)

Вторая (основная) задача динамики заключается в определении

уравнений движения точки, если известны действующие на нее силы

.

Рассмотрим движение точки относительно декартовой системы коор-

динат. Согласно (10.8), дифференциальные уравнения движения точки имеют

вид

( , , , , , , );

( , , , , , , ).

x

y

z

mx R x

y

zx

y

zt

m

y

Rx

y

zx

y

zt

mz R x

y

zx

y

zt

















&&&&

&

&&&&

&

&&

&&&

(10.20)

Для определения уравнений движения точки

(), (), ()

x

xt y yt z zt





необ-

ходимо проинтегрировать систему дифференциальных уравнений (10.20),

применив методы высшей математики.

Если удается это сделать, то получаем общее решение системы (10.20):







12 6

, , , ..., ;

, , , ..., ,

x

xt C C C

yy

t C C C

zzt C C C



(10.21)

где

С

1

, С

2

, …, С

6

 произвольные постоянные интегрирования. Дифферен-

цированием по времени решения (10.21) можно также определить проекции

скорости точки на декартовые оси:







12 6

, , , ..., ;

, , , ..., .

xxtCC C

y y t C C C

z z t C C C



&&

(10.22)

Для того чтобы из многообразия решений системы (10.21) выбрать то,

которое соответствует данной задаче, необходимо задать начальные условия

движения, т. е. в начальный момент времени зафиксировать положение точки

и проекции ее скорости на декартовые оси:













  

00 0

000

0; 0 ; 0 ; 0 ;

0 ; 0 ; 0 .

txx

yy

zz

xx

yy

zz

  

 

&& &&

&&

(10.23)

Совокупность данных (10.23) называется

начальными условиями движения.

Нахождение значений постоянных интегрирования С

1

, С

2

, …, С

6

про-

водится подстановкой начальных условий движения (10.23) в совокупность

выражений (10.21) и (10.22)







0126

0, , , ...,

xx CC C

yy C C C

zz C C C

xx CC C

yy C C C

zz C C C





























&&

и решения полученной системы шести алгебраических уравнений

относительно шести неизвестных

С

1

, С

2

, …, С

6

.

ЛЕКЦИЯ

11

ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ ТОЧКИ

Колебательные движения материальных тел и механических систем

имеют место в различных областях техники. Они сопровождают вибрации

машин и их деталей, вибрации инженерных сооружений и их отдельных

элементов, движения самолетов и автомобилей, и т. д.

Первоначально для установления основных параметров, влияющих на

характер колебательного движения, ограничимся рассмотрением только

прямолинейных колебаний тела,

приняв его за материальную точку.

В зависимости от действующих на материальную точку сил различают

три вида колебательных движений:

1)

свободные (гармонические) колебания, происходящие под дейст-

вием линейной восстанавливающей силы, т. е. силы стремящейся вернуть

точку в положение равновесия и пропорциональной её отклонению от этого

положения равновесия.

2)

затухающие колебания, происходящие под действием восстанавли-

вающей силы и силы сопротивления среды,

3)

вынужденные колебания, когда кроме восстанавливающей силы

и силы сопротивления среды действует сила, периодически зависящая от

времени.

Свободные колебания точки

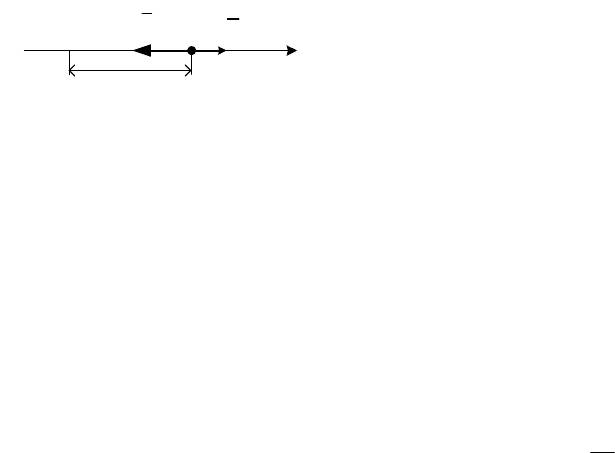
Рассмотрим материальную точку М массой m, движущуюся прямо-

линейно вдоль неподвижной оси

Ох под действием линейной восстанав-

ливающей силы

F

r

, всегда направленной к неподвижному центру О и по

закону Гука пропорциональной расстоянию от точки М до этого центра

(рис. 11.1), т. е.

x

F

cx





, (11.1)

где

c



коэффициент пропорциональности.

В дальнейшем в качестве линейной восста-

навливающей силы

F

r

будет рассматриваться сила

упругости пружины. В этом случае

c

является коэффициентом жесткости

пружины. В системе СИ

c

равен величине силы, которую надо приложить

к пружине для изменения ее длины на один метр.

Запишем основное уравнение динамики точки в проекции на ось Ох:

x

ma F



или

mx cx





&&

. (11.2)

Разделив (11.2) на m и введя обозначение

2

c

k

m



, представляем уравнение

в виде

2

0xkx





&&

, (11.3)

Уравнение (11.3) называется дифференциальным уравнением сво-

бодных колебаний при отсутствии сопротивления.

Будем искать решение линейного однородного дифференциального

уравнения второго порядка с постоянными коэффициентами (11.3) в виде

t

x

e





. Подставляя это решение в (11.3), получаем характеристическое

уравнение

22

σ 0k

, которое имеет мнимые корни

1,2

σ ki

. Тогда общее

решение дифференциального уравнения (11.3) принимает вид

**

12 1 2

cos sin

ikt ikt

x

Ce Ce C kt C kt



  

. (11.4)

Здесь

112

()/2CCC





,

112

()/2 CCC







постоянные интегрирования,

определяемые по начальным условиям движения материальной точки:

000

0 (0) , (0)txxxxV





&&

. (11.5)

Для удобства исследования движения (11.4) обычно постоянные интегри-

рования

1

C

и

2

C

заменяют другими постоянными

A

и

α

. Полагая, что

12

sin α, cosαCA CA



(11.6)

O

x

M

x

F

V

Рис. 11.1

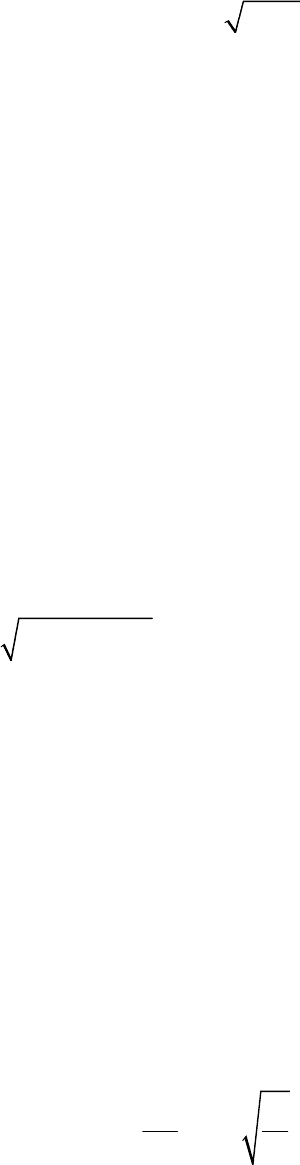
и подставляя (11.6) в (11.4), получаем

sin( α),xA kt





(11.7)

Колебания, совершаемые точкой по закону (7), являются гармоничес-

кими колебаниями.

Здесь величина

/kcm

(11.8)

называется круговой частотой (собственной частотой) свободных колеба-

ний, которая равна числу колебаний точки за время

2π

секунд.

Величина А является амплитудой,

αkt





фазой, 



начальной фазой

колебаний.

Вычислим скорость точки М:

cos( α)xAk kt





&

. (11.9)

Для определения постоянных интегрирования А и  подставляем на-

чальные условия движения (11.5) в (11.7) и (11.9) и получаем систему

алгебраических уравнений:

0

=sinα

cosα

xA

VAk









(11.10)

Решая (11.10) относительно

A

и

α

, найдем

222

00 00

/ , tgα /.

A

xVk kxV 

(11.11)

Из (11.11) следует, что значение амплитуды А и начальной фазы

α

свободных колебаний точки зависят от её начальных условий движения.

Промежуток времени Т, за который точка совершает одно полное

колебание, называется периодом колебаний. Согласно этому определению Т

из (7) и (9) следует, что











sin ( ) α sin α ,

cos ( ) α cos α .

AktT Akt

Ak k t T Ak kt

 



 

Одновременное выполнение этих условий возможно только, если

2πkT 

. Откуда находим

2π

m

T

kc



. (11.12)

Вид выражений (11.8) и (11.12) означает, что частота k и период Т

свободных колебаний точки от начальных условий движения не зависит. Это

свойство называется изохронностью, а свободные колебания точки



изохронными.

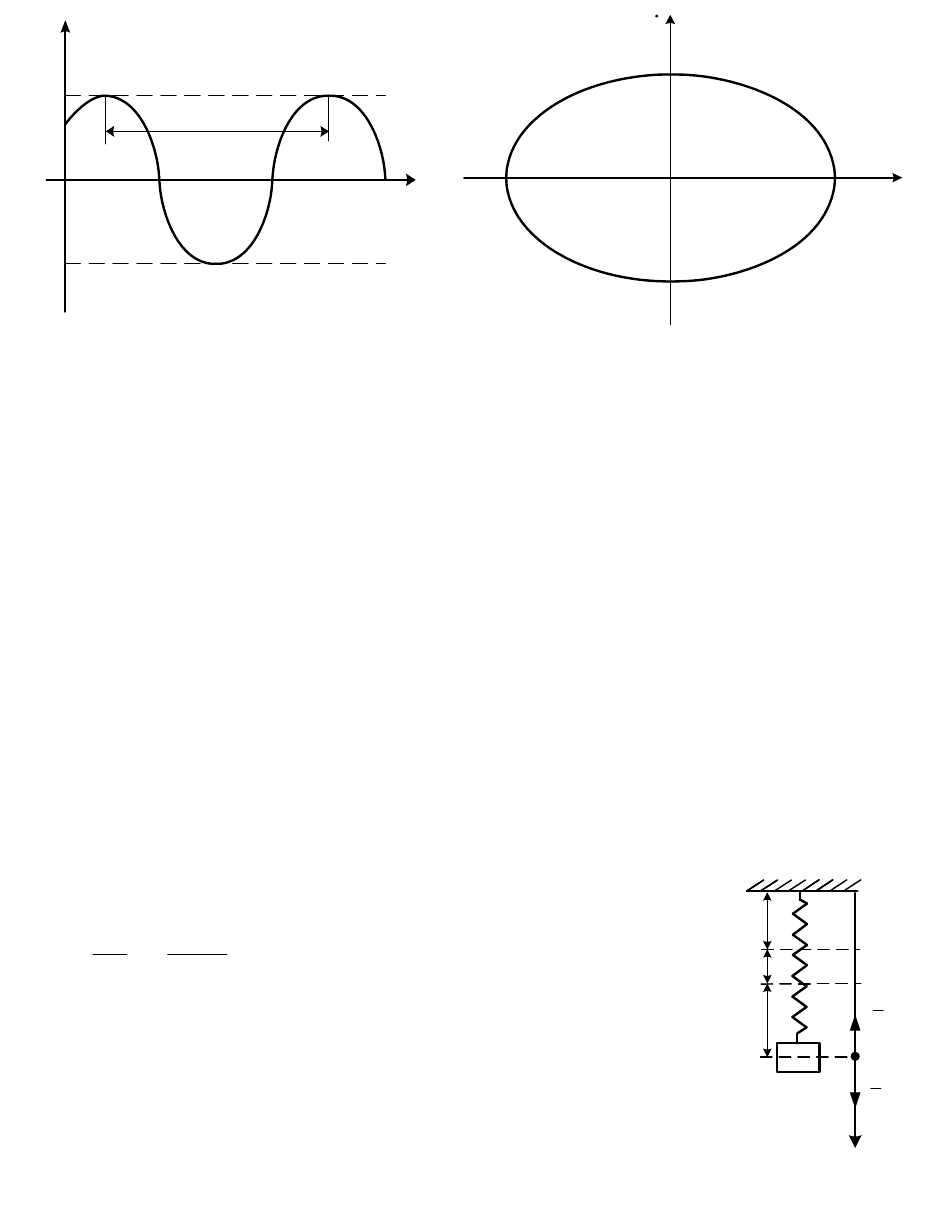
График гармонических колебаний (11.7) приведен на рис. 11.2, а. Сог-

ласно (11.7) координата

х материальной точки изменяется от

A



до А, т. е. ее

максимальное отклонение от центра О равно амплитуде А свободных

колебаний. Положение равновесия



точка О является центром колебаний:

в этой точке при х

= 0 восстанавливающая сила

F

r

обращается в ноль.

Для наглядного представления о характере прямолинейных колебаний

точки удобно применять следующую геометрическую интерпретацию.

Будем рассматривать координату

x

точки М и ее скорость

x

&

как

декартовые координаты точки плоскости, называемой фазовой плоскостью

(рис. 11.2, б). Каждая точка этой фазовой плоскости соответствующая

определенному состоянию материальной точки, называется изображающей

точкой, а ее координаты

x

и

x

&



координатами состояния. При движении

материальной точки М соответствующая ей изображающая точка описывает

на фазовой плоскости траекторию, называемую фазовой траекторией.

В случае свободных колебаний материальной точки, исключая время t

из зависимостей (11.7) и (11.9), получаем уравнение фазовой траектории

изображающей точки

22

222

1

xx

AAk



&

(11.13)

в виде эллипса, изображенного на рис. 11.2, б.

c

l

0

x

O

P

F

M

x

m



ст

O

1

Рис. 11.3

T

t

x

О

0

x

A

-A

x

О

Ak

-Ak

x

A

-A

а б

Рис. 11.2

Рассмотрим влияние постоянной силы на характер свободных

колебаний на примере задачи о свободных колебаниях тела М на пружине

жесткости

с (рис. 11.3).

В этом случае на материальную точку массой

m, кроме

восстанавливающей силы упругости пружины

F

r

, действует сила тяжести

P

mg

r

постоянная по модулю и направлению (

g



ускорение свободного

падения).

Для упрощения математического решения задачи начало отсчета

неподвижной оси Ох

выберем в положении статического равновесия тела на

пружине (рис. 11.3). В произвольном положении материальной точки

с координатой х величина полной деформации пружины (ее удлинение)

ст

δδ

x



, где

ст

δ 

величина деформации пружины в положении

статического равновесия О (на рис. 11.3 положение точки

1

O

соответствует

нижнему концу недеформированной пружины длиной

0

l

).

Тогда значение проекции силы упругости пружины на ось О

х

ст

(δ )

x

Fc x





. (11.14)

В положении статического равновесия О (

0x 

) величина

восстанавливающей силы равна

ст ст

δFc



и на материальную точку

действует уравновешенная сходящаяся система сил, для которой уравнение

равновесия

0

кx

F





(11.15)

принимает вид:

ст

0PF





.

Отсюда получаем

ст

δPc



, (11.16)

т. е. в положении статического равновесия сила тяжести уравновешивает

силу упругости пружины. Теперь запишем основное уравнение динамики

точки в проекции на ось Ох

xx

ma F P





или

ст

(δ )mx c x P





&&

. (11.17)

С учетом (11.16) уравнение (11.17) приведем к уравнению (11.2), а затем

представим в форме (11.3):

2

0xkx





&&

,

решение (7) которого не изменяется.

Следовательно, при рассмотрении движения тела М на пружине

положение статического равновесия О является центром колебаний для

материальной точки.

Обобщая эти результаты на случай действия на материальную точку

кроме восстанавливающей силы дополнительной произвольной постоянной

силы, приходим к следующему выводу: «Любая постоянная сила не

изменяет характера колебаний,

совершаемых материальной точкой под

действием восстанавливающей силы, а только смещает центр этих

колебаний в сторону действия этой постоянной силы на величину

статической деформа- ции

ст

δ

». Величина

ст

δ

определяется из формулы

аналогичной (11.16).

Подставляя (11.16) в (11.12), найдем период свободных колебаниях для

тела М на пружине

ст

δ

2πT

g



. (11.18)

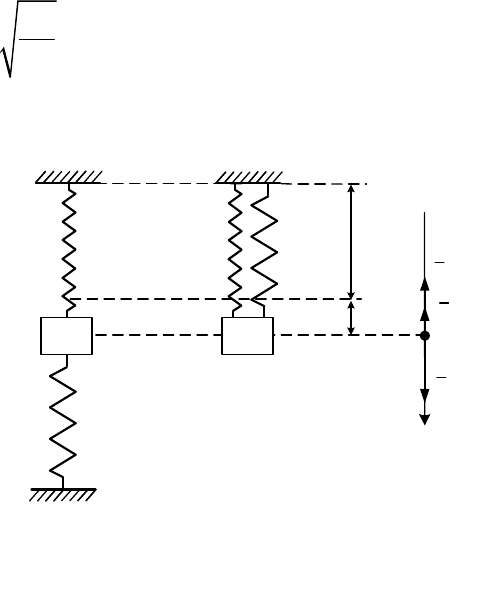
Рассмотрим случаи, когда тело М подвешено к системе пружин.

1. Если тело подвешено к двум

параллельно соединенным пружинам

жесткости

1

c

и

2

c

(рис. 11.4, а

и рис. 11.4, б), то эту систему

пружин заменим одной

эквивалентной пружиной с

жесткостью

c

(рис. 11.3). В

положении статического равновесия

О (

0x 

) для системы параллельно

соединенных пружин (рис.

11.4, в) уравнение равновесия (11.15)

принимает вид

1ст 2ст

0PF F 

или

1 ст 2 ст

δδ0Pc c





.

Отсюда

12ст

()δPcc





. (11.19)

l

0



ст

2

c

1

c

M

x

O

m

P

F

2 ст

F

2

c

1

c

M

1 с

т

а б в

Рис. 11.4

Валькова Т.А. и др. Теоретическая механика

Подождите немного. Документ загружается.