Валькова Т.А. и др. Теоретическая механика

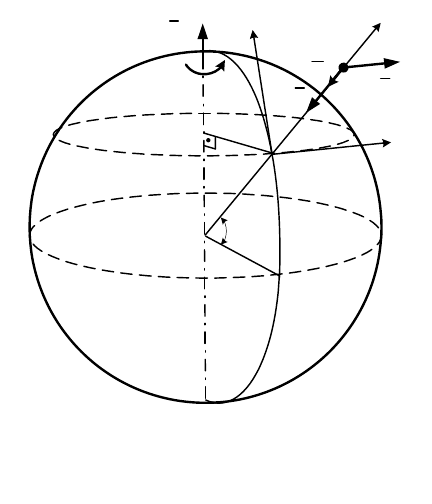
направления его движения. В южном полушарии отклонение будет

происходить влево от направления вектора его относительной скорости

r

V

r

.

Это обстоятельство является причиной размытия правых берегов рек,

текущих с юга на север в северном полушарии и левых берегов в южном

полушарии. В этом же состоит причина отклонения ветров постоянного

направлении (пассаты) и морских течений, а также циркуляции воздушных

масс.

Если точка движется по параллели на восток, то вектор ускорения

Кориолиса

C

a

r

будет направлен по радиусу параллели r к оси вращения

Земли, а кориолисова сила инерции

Ф

C



r

в противоположную сторону (от

оси). Вертикальная составляющая этой силы, параллельная радиусу ВС,

вызовет незначительное уменьшение веса точки.

Рассмотрим падение материальной точки В без начальной скорости

с высоты h вблизи поверхности Земли под действием силы тяжести

P

r

,

которую будем считать постоянной (рис. 13.4); сопротивлением воздуха

пренебрегаем.

Запишем основной закон динамики относительного движения (13.14)

для нашей задачи

Ф

C

ma P

rr

r

. (13.15)

Введем декартовую систему

координат Охуz, связанную с Землей:

ось Oz направим на широте  по

вертикали, ось Ох направим на восток, а

ось Оу



на север.

В произвольном положении

свободно падающей точки В вектор

относительной скорости

r

Vxiyjzk





r

rr

&&

&

по направлению близок

к вертикали данного места. Поэтому

кориолисова сила инерции

Ф

C

r

направлена почти по оси Ох. Проецируя

(13.15) на выбранные координатные оси, получим дифференциальные

уравнения относительного движения точки:

2 (cos sin);

2 sin;

2 cos.

e

mx m z y

my m y

mz mg m x

   





  





   



&&&

&

&&&

&

&&

(13.16)

B

S

N





е

C

Ф

V

r

C

O

P

x

y

z

Рис. 13.4

Здесь проекции кориолисовой силы инерции

Ф 2 ω

С er

mV





rr

r

вычислены

в декартовой системы координат Охуz.

Проинтегрируем систему (13.16), воспользовавшись методом

послевательных приближений.

Так как угловая скорость Земли

-1

ω 0,000073 c

e



очень мала, то сначала

интегрирование проведем, полагая

ω 0

e



(для свободно падающего тела

величина кориолисовой силы инерции

Ф

С

r

будет много меньше веса

mg

)

111

, ,

x

xyyzz

.

Тогда система (13.15) принимает вид

1

0;

.

mx

my

mz m

g





&&

(13.17)

Интегрируя (13.17) при начальных условиях движения

111

(0) 0, (0) 0, (0) ,

(0) 0, (0) 0, (0) 0,

x

yzh

xyz









&&

&

(13.18)

получим

111

2

111

0, 0, ,

0, 0, / 2.

xyzgt

xyzhgt



&&

&

(13.19)

Теперь найдем поправки к этому приближению, полагая

12 1 2 12

, , .

x

xx yyy zzz  

(13.20)

Подставляя (13.20) в (13.16) с учетом (13.19) получим систему

дифференциальных уравнений относительно

222

, ,

x

yz

:

2

2cos,

0,

0.

e

xgt

y

z







&&

(13.21)

Интегрируя (13.21) при нулевых начальных условиях, находим

2

222

3

122

cos , 0, 0,

cos , 0, 0.

3

e

xgt y z

gt

xyz

   





&&

&

(13.22)

Подставляя (13.19) и (13.22) в (13.20), получим уравнения движения

свободно падающей точки В:

32

cos , 0, .

32

e

gt gt

xyzh





(13.23)

Определяя из третьего уравнения (13.23) время свободном падении

материальной точки В с высоты h на Землю (

0z



)

2h

t

g



и подставляя его в первое уравнение (13.23), найдем формулу для

вычисления полного отклонения точки к востоку

3

2

cos

3

e

gh

xt

g

















. (13.24)

Поскольку модуль кориолисовой силы инерции много меньше веса тела mg,

то величины этих отклонений малы и заметны при свободном падении

только с достаточно большой высоты. Например, на широте Москвы

(

o

56

) при падении с высоты h = 100 м величина отклонения к востоку х =

1,2 см.

ЛЕКЦИЯ 14

ВВЕДЕНИЕ В ДИНАМИКУ МЕХАНИЧЕСКОЙ СИСТЕМЫ

Механической системой называется совокупность материальных

точек (тел), движение которых рассматривается.

Системы материальных точек бывают неизменяемые и изменяемые.

Система называется неизменяемой, если расстояние между любыми двумя ее

точками остается постоянным при движении (например, абсолютно твердое

тело). Если расстояние между двумя точками системы изменяется при ее

движении, то система называется изменяемой

.

Для механической системы, состоящей из n

материальных точек, силы

активные

а

к

F



(к = 1, 2, …, n) и реакции связей

к

N



, действующие на систему,

разделяются на внутренние и внешние силы. Внутренними силами

i

к

F



назы-

ваются силы взаимодействия между точками (телами) системы. Внешними

силами

е

к

F



называются силы, действующие на точки системы со стороны

точек (тел), не входящих в состав рассматриваемой системы. Такое деление

является условным и зависит от того, какая механическая система изучается.

Свойства внутренних сил

1. Геометрическая сумма (главный вектор) всех внутренних сил

системы равняется нулю.

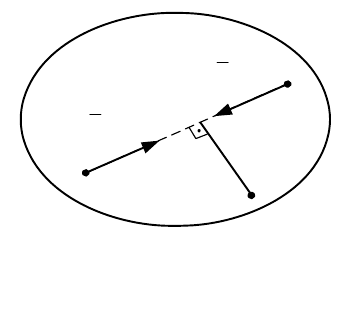
Действительно, согласно закону равенства действия и противодействия

любые две точки В

1

и В

2

системы действуют друг на друга силами

12 21

ii

FF





rr

(рис. 14.1) так, что

12 21

0

ii

FF





rr

. (14.1)

Поскольку результат (14.1) имеет место для

любой пары точек системы, то,

следовательно,

1

0

n

ii

к

FF







rr

. (14.2)

2. Сумма моментов (главный момент)

всех внутренних сил системы относительно

произвольного центра или оси равняется

нулю.

На рис. 14.1 видно, что если взять произвольный центр О, то

21 12

m( ) m( )

ii

OO

F F

rr

, поэтому

21 12

m ( ) m ( ) 0

ii

OO

FF





rr

. (14.3)

Аналогичный результат можно получить для сил

i

F

12



и

i

F

21



при вычислении

суммы их моментов относительно любой оси. Следовательно, для всех

внутренних сил системы

1

Mm ()0

n

ii

OOк

к

F







rr

r

и

1

Mm ()0

n

ii

zzк

к

F





r

. (14.4)

Отметим, что согласно (14.2) и (14.4) внутренние силы образуют

уравновешенную систему сил только для неизменяемой системы (абсолютно

твердое тело). Для изменяемой системы внутренние силы, приложенные

к разным материальным точкам (телам), могут привести к их взаимным

O

B

1

h

F

21

i

F

12

i

B

2

Рис. 14.1

перемещениям, и в этом случае система внутренних сил не будет

уравновешенной.

Центр масс механической системы

Движение механической системы зависит от ее суммарной массы и

распределения масс точек системы в пространстве. Масса системы М равна

сумме масс всех точек (тел), входящих в систему:

1

n

к

M

m





. (14.7)

Геометрическая точка С, положение которой определяется радиус-

вектором:

1

n

кк

к

C

mr

r

M





r

, (14.8)

называется центром масс (центром инерции) механической системы.

Проецируя (14.8) на декартовые оси, получим

1

,

n

кк

к

C

mx

x

M





1

,

n

кк

к

C

my

y

M





1

.

n

кк

к

C

mz

z

M





(14.9)

В (14.8) и (14.9)

к

r



и х

к

, у

к

, z

к

 соответственно радиус-вектор и декартовые

координаты к-й материальной точки системы. При непрерывном

распределении массы суммы в формулах (14.8) и (14.9) переходят в

соответствующие интегралы.

В однородном поле сил тяжести, когда размеры частиц твердого тела

много меньше радиуса Земли, центр масс тела совпадает с его центром

тяжести. Действительно, если умножить числитель

и знаменатель правой

части (14.8) на величину ускорения силы тяжести

g , то получим формулу

11

nn

кк кк

кк

C

m

g

rpr

r

Mg P





rr

r

, (14.10)

которая согласно (9.8) определяет положение центра тяжести твердого тела.

Здесь

gmp

кк



и

g

M

P 

 вес к-й точки и вес всего тела соответственно.

Следовательно, вблизи Земной поверхности центр масс твердого тела

совпадает с его центром тяжести, способы определения которого были

изложены выше (см. лекция 9).

В отличие от центра тяжести понятие о центре масс сохраняет свой

смысл для тела, находящегося в произвольном силовом поле. Следовательно,

центр масс как характеристика распределения массы в пространстве имеет

смысл для любой механической системы.

Моменты инерции

Кроме координат центра масс (14.9) суммарными характеристиками

распределения масс в пространстве являются моменты инерции.

Моментом инерции системы (тела) относительно полюса О

(полярным моментом инерции) называется положительная величина, равная

сумме произведений масс точек системы (тела) на квадрат их расстояний до

этого полюса (рис. 14.2):

2

1

n

O кк

к

I

mr





, (14.11)

где

к

r

 модуль радиус-вектора

к

r

к-й точки, проведенного из точки О.

Моментом инерции системы (тела) относительно оси z (осевым

моментом инерции) называется положительная величина, равная сумме

произведений масс точек системы (тела) на квадрат их расстояний до этой

оси:

2

1

n

z ккz

к

I

mh



 . (14.12)

Здесь

кz

h

 длина перпендикуляра, опущенного из к-й точки на ось z. В

системе СИ единицей измерения осевого момента инерции является 1 кг м

2

.

Для одной материальной точки, находящейся на расстоянии h от оси,

2

hmI

z



. Для тел сложной формы момент инерции

z

I

можно представить в

виде

2

ρ

zz

IM

, (14.13)

где

ρ

z

 положительная величина,

называемая радиусом инерции тела

относительно оси z; М  масса тела.

При вычислении осевых моментов

инерции тела (системы) относительно

декартовых осей Охуz следует квадраты

рас-стояний от точек до осей выразить

через их координаты: для к-й точки

системы массой m

к

с координатами х

к

, у

к

, z

к

O

y

x

к

z

к

y

h

кz

x

кx

кy

z

m

к

r

к

Рис. 14.2

222

кккx

zyh 

,

222

кккy

zхh 

,

222

кккz

ухh





(рис. 14.2). Тогда согласно (14.11)

получим



222

11

222

11

222

11

;

.

nn

x ккx кк к

кк

nn

y ккy кк к

кк

nn

z ккz кк к

кк

Imh myz

Imhmxz

Imh mxy



 



(14.14)

Учитывая, что

2222

кккк

rxyz

из (14.11) и (14.14) следует зависимость

2

Oxyz

IIII





. (14.15)

В случае сплошного твердого тела объема V, разбивая его на

элементарные объемы с массой

к

m



и устремляя их к нулю, находим

z

I

:



22

0

1

lim

к

n

z кк к

m

к

Imxy









22 22

(V) (V)

()

γ

() V

x

ydm x yd  



, (14.16)

где

γ Vdm d

; а

γ

 объемная плотность вещества. Для однородных тел, так

как

γ = const

, то формула (14.16) принимает более простой вид





22

(V)

γ

V

z

Ixyd



. (14.17)

Выражения аналогичные (14.17) можно легко найти для

x

I

и

y

I

:







22

(V)

22

(V)

γ

V ;

γ

V .

x

y

Iyzd

Ixzd





(14.18)

Вычислим моменты инерции некоторых однородных тел.

1. Для тонкого круглого однородного кольца массой М радиусом R

момент инерции относительно оси С

z

, перпендикулярной плоскости кольца и

проходящей через его центр С (рис. 14.3, а) определим по формуле (14.12)

(

const

кz

hR

):

2

n

1к

2

кz

RMRmI 





. (14.19)

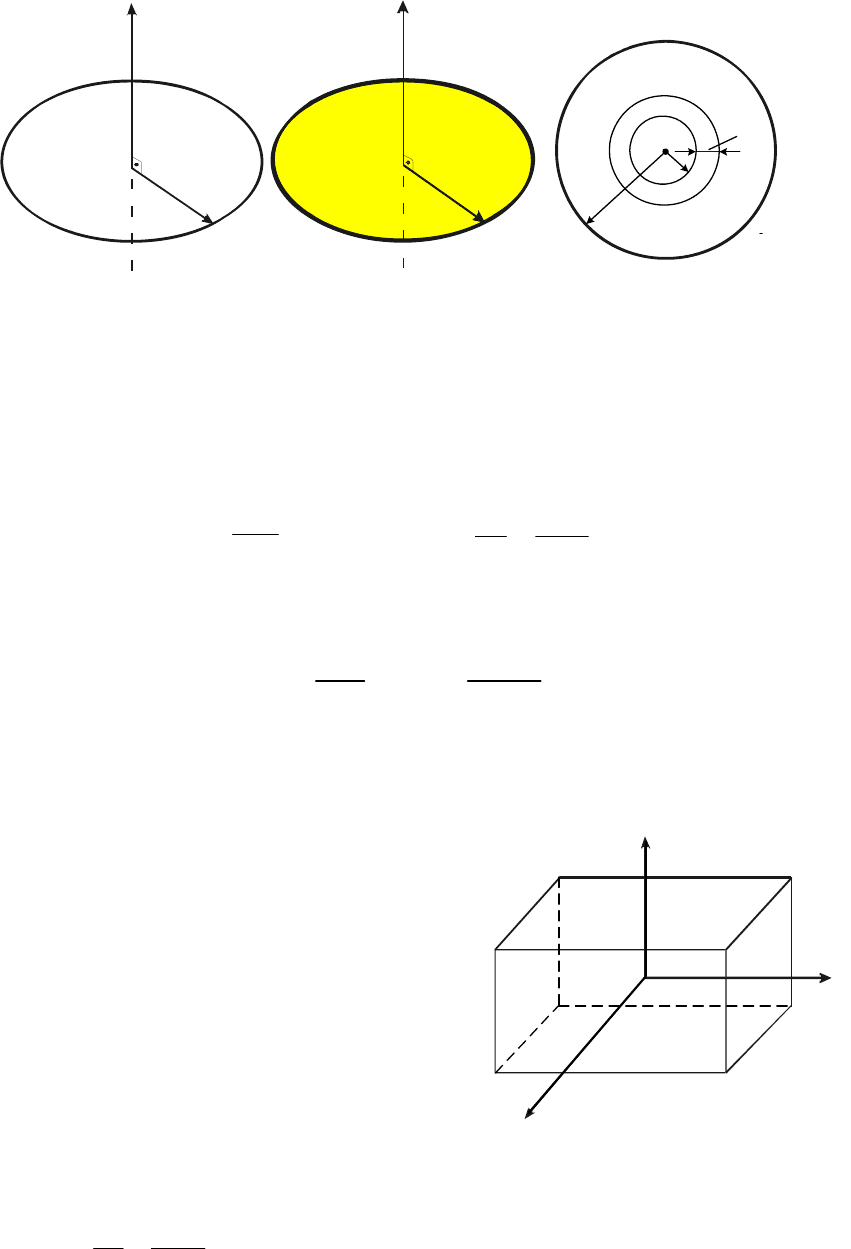
Такой же результат можно получить для момента инерции тонкой

однородной цилиндрической оболочки массой М и радиусом R относительно

ее центральной оси симметрии.

C

R

z

C

R

z

dr

r

R

C

а б в

Рис. 14.3

2. Для круглой однородной пластины массой М и радиусом R вычислим

момент инерции относительно центральной оси С

z

, перпендикулярной

пластине (рис. 14.3, б). Выделим элементарное кольцо радиусом

r и

толщиной dr

(рис. 14.3, в). Масса этого кольца площадью

2π dS r dr

равна

σ dm dS

2

σ2π

M

rdr rdr

R



, где

2

σ

π

M

SR



 масса единицы

площади пластины. Так как расстояние от выделенного элементарного

кольца до оси С

z

равно r, то находим

2

23

2

0

2

R

Cz

M

MR

Irdm rdr

R

 



. (14.20)

Аналогичный результат можно получить при вычислении момента инерции

однородного цилиндра массой М и радиусом R относительно центральной

оси симметрии.

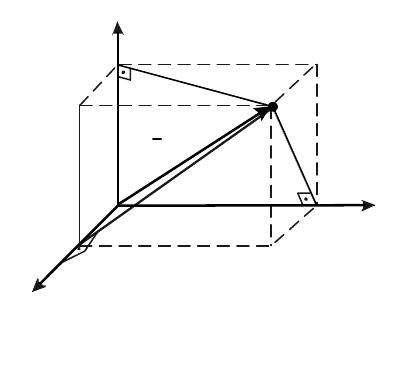
3. Для однородного прямоугольного

параллелепипеда массой М со сторонами l,

a, b определим момент инерции

относительно осей Сx, Cy Cz, проходящих

через центр масс С и параллельных его

ребрам (рис. 14.4).

Воспользуемся формулами (14.17) и

(14.18). Для этого разобьем

параллелепипед на элементарные объемы

в форме прямоугольных

параллелепипедов со сторонами dx

, dy и dz. Тогда

Vddxdydz





, а объемная

плотность

γ

V

M

lab



. Согласно (14.17)

b

l

a

C

x

z

y

Рис. 14.4



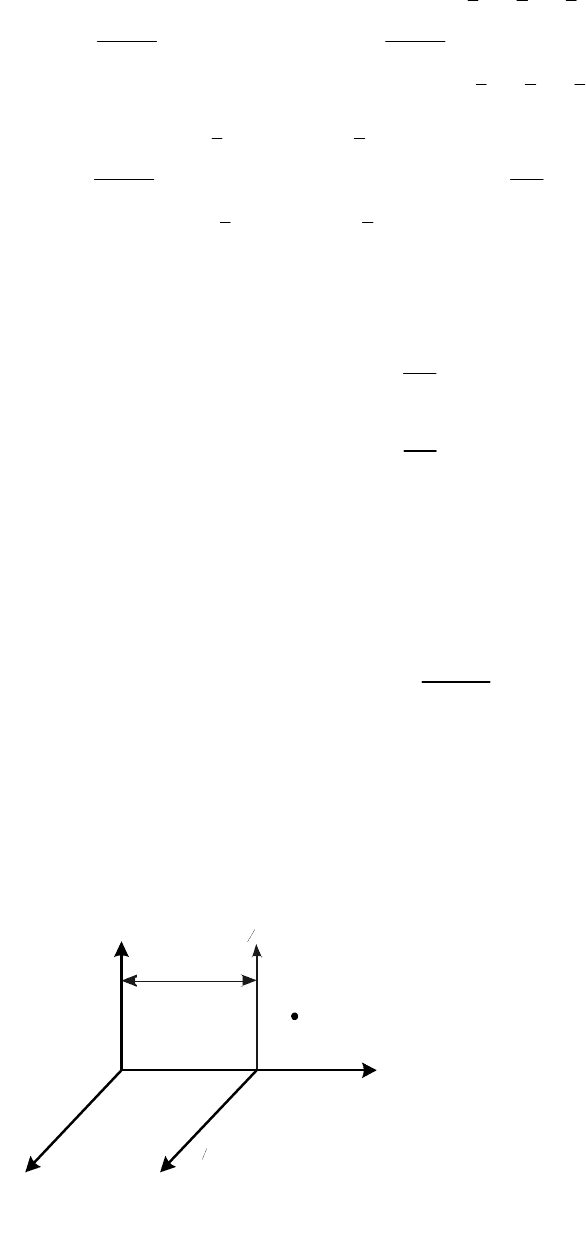
222

22 22

(V)

222

22

22 22

22

V ()

12

bal

Cz

bal

la

MM

I x y d x y dx dy dz

lab lab

MM

ba x dx bl y dy l a

lab





 

















(14.21)

Проведя аналогичные вычисления по формулам (14.18), получим



22

;

12

.

12

Cx

Cy

M

Iab

M

Ilb



Чтобы найти момент инерции тонкого однородного стержня длиной l

относительно оси С

z

, перпендикулярную стержню и проходящую через его

середину, следует в формуле (14.21) положить a = 0:

2

.

12

Cz

Ml

I 

(14.22)

Иногда для определения моментов инерции твердых однородных тел

удобно пользоваться

теоремой Гюйгенса: момент инерции тела

относительно данной оси равен моменту инерции относительно оси, ей

параллельной, проходящей через центр масс С тела, сложенному с

произведением массы всего тела на квадрат расстояния между осями, т. е.

2

zCz

IIM d





, (14.23)

где d  расстояние между осями (рис. 14.5).

Доказательство. Поместим начало

координат в центре масс С тела,

направив ось

Cz

по оси, относительно

которой момент инерции

Cz

I

известен, а

ось

Cy так, чтобы она пересекала ось

Cz



, параллельную оси

Cz

(рис. 14.5).

Тогда согласно (14.12)

y

x

C

d

z

A

B

(

x

к

,

y

к

,

к

z

)

x

z

Рис. 14.5

2

22 2

11

2

222

111

() () ( )

( ) 2 ( ) .

nn

z кк к кк к

кк

nnn

кк к кк к Cz

ккк

Imxy mxyd

mx

y

dm

y

md I Md

















  





Так как с учетом (14.12) первая сумма в полученном выражении есть

Cz

I

. Из

(14.9)

1

0

n

кк C

к

my My





, поскольку центр масс С находится в начале

координат;

1

n

к

mM





 масса тела. Справедливость теоремы (14.23)

доказана. Следовательно, из всех осей данного направления наименьший

момент инерции будет относительно оси, проходящей через центр масс.

Из (14.23) следует соотношение между моментами инерции

относительно любых параллельных осей

z

1

и z

2

:

12

22

12

()

zz

IIM dd 

, (14.24)

где d

1

и d

2

 расстояние от центра масс С до осей z

1

и z

2

соответственно.

Величины

x

y

I

,

yz

I

,

zx

I

, определяемые равенствами

11 1

, ,

nn n

xy кк к yz ккк zx ккк

кк к

I

mxy I myz I mzx

 





(14.25)

называются центробежными моментами инерции. Согласно (14.25) они

могут иметь любой знак и обращаться в нуль.

Ось Оz, для которой

0

xz

I



и

0

yz

I



, является главной осью инерции

относительно полюса О. Главной центральной осью инерции называется

главная ось инерции, проходящая через центр масс С тела.

Отметим два частных случая, когда характер оси отражает симметрию

тела.

1. Если тело имеет плоскость материальной симметрии, то для всех её

точек ось, перпендикулярная к плоскости симметрии является главной

осью

инерции.

2. Если тело имеет ось материальной симметрии, то эта ось является

главной центральной осью инерции.

ЛЕКЦИЯ 15

ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

Дифференциальные уравнения движения

Валькова Т.А. и др. Теоретическая механика

Подождите немного. Документ загружается.