Валькова Т.А. и др. Теоретическая механика
Подождите немного. Документ загружается.

механической системы
Рассмотрим несвободную систему, состоящую из n материальных то-
чек. Воспользуемся принципом освобождаемости от связей и заменим их
действие реакциями связей
к
N
(к = 1, 2, …, n). Для произвольной к-й точки
системы с массой m
к
обозначим через
е
к
F
равнодействующую всех внешних
сил (активных и реакций связей), действующих на точку:
е a
кк к
F
FN
rrr
;
а через
i
к
F
равнодействующую приложенных к ней внутренних сил. Запи-
шем для каждой точки системы основной закон динамики в форме (10.7):
11 1 1
22 2 2
;
;
.........................
.
е i
е i
ei
nn n n
mr F F
mr F F
mr F F
rr
r
&&
rr
r
&&
rr
r
&&
(15.1)
Уравнения (15.1) называются дифференциальными уравнениями
движения механической системы в векторной форме. В проекциях на оси
неподвижной декартовой системы координат уравнения (15.1) принимают
вид
,
,
.
е i
к к кх кх
е i
к к ку ку
ei
кк кz кz
mx F F
m
у
FF
mz F F
&&
rr
&&
rr
&&
(к = 1, 2, …, n) (15.2)
В общем случае входящие в скалярные уравнения (15.2) силы могут быть
функциями времени, координат и скоростей точек системы.
Основная задача динамики системы заключается в определении закона
движения каждой точки системы и нахождении реакций наложенных на нее
связей. Для ее решения требуется проинтегрировать систему 3n
дифференциальных уравнений (15.2) и найти 6n постоянных интегрирования
по начальным условиям движения (задача Коши).
Основными недостатками такого метода изучения движения
механической системы являются:
1. Число уравнений системы (15.2) зависит от количества n
материальных точек, входящих в механическую систему. Найти общее
решение уравнений (15.2) в аналитическом виде удается лишь в частных
случаях, когда число точек
системы мало. Если n велико, то для решения
задачи приходится использовать численные методы.
2. Правые части уравнений (15.2) содержат внутренние силы и реакции
связей, аналитические выражения для которых, как правило, не известны.
Однако при практическом исследовании движения часто нет
необходимости решать уравнения (15.1) и (15.2), а достаточно знать
изменение со временем некоторых величин, общих для всей механической
системы. Такие величины, являющиеся в общем случае функциями
координат, скоростей,
времени и остающиеся постоянными при движении
системы, называются первыми интегралами уравнений движения (15.1).
Знание первых интегралов позволяет получить существенные сведения
относительно физической картины изучаемого движения, и эти сведения
в ряде случаев могут иметь больший интерес, нежели точное решение
системы (15.1).
Первые интегралы можно найти из так называемых общих теорем
динамики, когда выполняются
дополнительные условия для действующих
сил. Кроме того, общие теоремы динамики, являющиеся следствиями
уравнений (12.1), дают сведения о движении механической системы в целом.
Перейдем теперь к рассмотрению этих теорем.
Теорема о движении центра масс
Если система состоит из перемещающихся друг относительно друга
материальных точек (тел), то положение центра масс С
системы может
изменяться. Найдем закон движения центра масс. Складывая, левые и правые
части уравнений (15.1), получим
111
nnn
е i
кк к к
ккк
mr F F
rr
v
&&
. (15.3)
Из (14.8) имеем
1
n
кк C
к
mr M r
r
v
.
Дважды вычисляя от обеих частей данного равенства производную по
времени и пользуясь свойством, что производная от суммы равна сумме
производных, находим
1
n
кк CC
к
m r Mr Ma
rr
v
&&
&&
, (15.4)
где
C
a
ускорение центра масс системы. По свойству внутренних сил (14.1)
1
0
n
i
к
к
F
r
. Тогда с учетом (14.1) и (15.4) уравнение (15.3) принимает вид

1
n
е
C к
к
M
aF
r
r
. (15.5)
Уравнение (15.5) выражает
теорему о движении центра масс системы:
центр масс механической системы движется как материальная точка
с массой, равной массе системы, под действием внешних сил системы.
Проецируя (15.5) на координатные оси, получим
1
1
1
;
;
.
n
е
C кх
к
n
е
C кy
к
n
е
C кz
к
M
xF
M
yF
M
zF
&&
&&
&&
(15.6)
Уравнения (15.6) называются дифференциальными уравнениями движения
центра масс в проекциях на оси декартовой системы координат.
Следствия:
1. Одними внутренними силами нельзя изменить характер движения
центра масс системы. Внутренние силы могут оказать влияние на движение
центра масс лишь опосредованно через внешние силы.
2. Если геометрическая сумма внешних сил, действующих на систему,
равна нулю, то центр масс механической системы движется равномерно
и прямолинейно или находится в покое.
Действительно,
если
1
0
n
е
к
к
F
r
, то
2
2
0
CC
dr dV
MM
dt dt
r
r
.
Отсюда
0
const
CC
VV
rr
, (15.7)
где
0
C
V
r
начальная скорость центра масс.
3. Если сумма проекций всех внешних сил на некоторую неподвижную
ось равна нулю, то проекция скорости центра масс на эту ось есть величина
постоянная.
Пусть
1
0
n
е
кх
к
F
, из первого уравнения (15.6) имеем
0
C
M x
&&
. Отсюда
const .
CCx
xV
&
(15.8)

Выражения (15.7) и (15.8) являются законами сохранения движения центра
масс и представляют собой первые интегралы соответственно уравнений
(15.1) и (15.2).
4. Пара сил, приложенная к твердому телу, не может изменить
движение его центра масс (она может вызвать только вращение тела).
Теорема о движении центра масс системы дает обоснование методам
динамики материальной точки. Принимая
тело за материальную точку, и
изучая ее движение, мы фактически определяем движение центра масс этого
тела. Если тело движется поступательно, то его движение полностью
определяется движением центра масс. В других случаях тело можно принять
за материальную точку, если при решении задачи можно пренебречь
вращательной частью движения твердого тела.
Количество движения материальной точки. Теорема
об изменении количества движения материальной точки
Одной из мер механического движения материальной точки является ее
количество движения.
Количеством движения материальной точки называется векторная
величина
Vm
, равная произведению массы точки на вектор ее скорости.
Век-тор
Vm
направлен так же, как вектор скорости точки, по касательной к
ее траектории. В системе СИ единицей измерения количества движения
является 1 кг м /c =1 H c.
Запишем основной закон динамики (10.4):
1
n
к
к
ma F
r
r
.
Так как масса точки постоянна, а ее ускорение
/adVdt
r
r
, то (10.4) можно
представить в виде
1
n
к
к
dmV
F
dt
r
r
(15.9)
Уравнение (15.9) представляет теорему об изменении количества
движения материальной точки в дифференциальной форме
: производная
по времени от количества движения материальной точки равна
геометрической сумме действующих на нее сил.
Умножив (15.9) на dt, получим
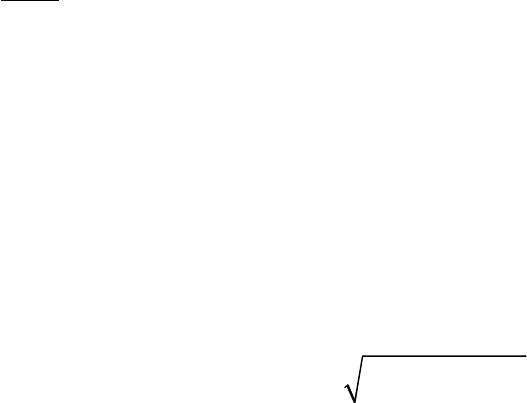
11
nn
кк
кк
d mV F dt dS
r
rr
. (15.10)
Здесь векторная величина
dtFSd
кк
называется элементарным импульсом
силы, который характеризует действие силы
к
F
на материальную точку за
время
d
t
. Полный импульс силы
к
F
за время t
1
определяется по формуле
1
0
.
t
кк
SFdt
r
r
(15.11)
В частном случае, если сила
к
F
постоянна по модулю и направлению
const
к
F
r
, то
1кк
SFt
r
r
. (15.12)
В общем случае модуль импульса силы
к
F
за время t
1
может быть вычислен
по его проекциям на декартовые оси:
111
000
; ; ;
ttt
кх кх кy кy кz кz
S F dt S F dt S F dt
222
ккx кy кz
SSSS
.
Импульс силы является мерой такого ее действия, который
характеризует передачу материальной точке механического движения со
стороны действующих на нее тел за определенный промежуток времени.
Действительно, пусть движущаяся точка имеет в момент времени t = 0
скорость
0
V
, а в момент t
1
скорость
1
V
r
. Вычислив от обеих частей равенства
(15.10) определенные интегралы, получим
1
10
1
0
t
n
к
к
mV mV F dt
rr r
,
или
10
1
n
к
к
mV mV S
r
rr
. (15.13)
Уравнение (15.13) выражает
теорему об изменении количества
движения материальной точки в конечной форме
: изменение количества
движения материальной точки за некоторый промежуток времени равно

геометрической сумме импульсов всех действующих на точку сил за тот же
промежуток времени.
Проецируя равенство (15.13) на декартовые оси, получаем
10
1
10
1
10
1
;
;
.
n
xx кx
к
n
yy кy
к
n
zz кz
к
mV mV S
mV mV S
mV mV S
(15.14)
В случае прямолинейного движения точки, происходящего вдоль оси х,
теорема выражается первым из этих уравнений.
Количество движения механической системы. Теорема
об изменении количества движения механической системы
Одной из динамических величин, характеризующих движение
механической системы, является ее количество движения.
Количеством движения механической системы называется вектор
Q
,
равный геометрической сумме (главному вектору) количества движения
точек системы:
n
к
кк
VmQ
1
. (15.15)
Поскольку
C
C
C
n
к
кк
n
к
к
к
n
к
кк
VM
dt
rd
MrM
dt
d
rm
dt
d
dt
rd
mVm
111
,
так как из (14.8)
n
к
Cкк
r Mrm
1
. Тогда
C
QMV
r
r
, (15.16)
т. е. количество движения механической системы равно массе системы,
умноженной на вектор скорости ее центра масс.
Из (15.16) следует, что если при движении тела (системы) центр масс
остается неподвижным, то количество движения тела (системы) равно нулю.
Например, количество движения тела, вращающегося вокруг неподвижной
оси, проходящей через его центр масс С,
будет равно нулю.

Следовательно, количество движения является характеристикой
поступательного движения системы (твердого тела), а при сложном
движении
характеристикой поступательной части движения вместе с
центром масс.
Проецируя (15.16) на координатные оси, получаем
;
;
.
x
Cx C
yCyC
zCzC
QMV Mx
QMV My
QMV Mz
&
&
&
(15.17)
Проекция количества движения механической системы на каждую
координатную ось определяется произведением массы системы на проекцию
скорости центра масс на эту ось.
В отличие от вектора количества движения материальной точки
Vm
,
который приложен к самой движущейся точке, вектор количества движения
механической системы Q
является свободным вектором.
Продифференцируем (15.16) по времени:
C
C
dQ dV
M
Ma
dt dt
r
r
r
. (15.18)
Согласно теореме о движении центра масс (15.5)
1
n
е
C к
к
M
aF
r
r
, тогда (15.18)
принимает вид
.
e
n
1к
е
к
FF
dt
Qd
(15.19)
Здесь
e
F
главный вектор внешних сил системы.
Уравнение (14.19) выражает
теорему об изменении количества
движения механической системы в дифференциальной форме
:
производная по времени от количества движения механической системы
равна главному вектору внешних сил.
Фактически формула (15.19) представляет собой еще одну форму
теоремы (15.5). Уравнение (15.19) в проекциях на декартовые оси имеет вид
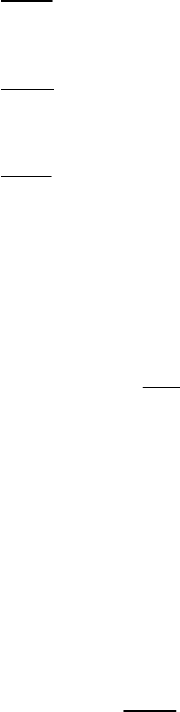
1
1
1
;
;
.
n
е e
x
кxx
к
n
y
е e
кyy
к
n
е e
z
кzz
к
dQ
F
F
dt
dQ
F
F
dt
dQ
F
F
dt
(15.20)
Следствия.
1. Если главный вектор внешних сил равен нулю, то количество
движения механической системы остается постоянным. Из уравнения
(15.19) следует, что если
0
e
F
r
, то
0
dQ
dt
r
, т. е.
const
C
QMV
uuuuur
r
r
. (15.21)
2. Если проекция главного вектора внешних сил на какую-нибудь ось
равна нулю, то проекция количества движения механической системы на
эту ось постоянна. Например, если
0
e
x
F
, то из первого уравнения (15.20)
0
x
dQ
dt
,
тогда
const
xCx
QMV
. (15.22)
Следствия (15.21) и (15.22) выражают законы сохранения количества
движения механической системы, которые представляют собой первые
интегралы уравнений движения.
Применим этот закон для объяснения принципа реактивного движения.
Пусть на систему, состоящую из двух сочлененных тел, находящихся в
покое, не действуют внешние силы. Тогда согласно (15.21)
const 0Q
uuuuur
r
.
Если при действии внутренних сил (например, подрыва пиропатрона)
первому телу массой m
1
сообщим скорость
1
V
r
, то скорость второго тела
2
V
r
массой m
2
можно определить из закона сохранения количества движения
системы:
11 2 2
0Qm V m V
r
rr
.
Отсюда

1
21
2
m
VV
m
rr
,
т. е. второе тело будет двигаться в сторону, противоположную первому телу.
Если этому движению препятствует какая-нибудь связь, то второе тело будет
давить на эту связь с реактивной силой, направленной по
2
V
r
. В реактивных
двигателях реактивная сила создается за счет истечения газа с большой
скоростью (
2
V
~ 22,5 км/c) из сопла двигателя.
Получим еще одну форму теоремы об изменении количества движения
системы. Пусть при t
= 0 количество движения системы
0
Q
, а в момент
времени t = t
1
1
Q
r
. Тогда, умножая (15.19) на dt и интегрируя, получим
1
10
1
0
t
n
е
к
к
QQ Fdt
rr
r
или с учетом (15.11)
10
1
n
е
к
к
QQ S
rr r
. (15.23)
Уравнение (15.23) выражает
теорему об изменении количества
движения системы в конечной форме
: изменение количества движения
системы за некоторый промежуток времени равно геометрической сумме
импульсов внешних сил, действующих на систему за тот же промежуток
времени.
В проекциях на координатные оси (15.23) принимает вид
10 10 10
11 1
; ; .
nn n
ее е
xx кx уу ку zz кz
кк к
QQ S QQ S QQ S
(15.24)
Внутренние силы явно не входят в теорему об изменении количества
движения системы в любой из ее форм и, следовательно, непосредственно
не влияют на изменение ее количества движения.
Однако в изменяемых системах внутренние силы могут вызвать
движение отдельных частей системы и вследствие этого привести к
изменению внешних сил реакций внешних
связей, которые могут изменить
ее количество движения.
ЛЕКЦИЯ 16
Момент количества движения
материальной точки и механической системы
Важной динамической характеристикой материальной точки является
ее момент количества движения.
Моментом количества движения материальной точки относительно
произвольного центра О называется вектор
)(m
O
Vm
, определяемый равенством
m( )
O
mV r mV
rr
r
r
, (16.1)
где
r
радиус-вектор материальной точки В, проведенный из неподвижного
центра О.
O
B
h
h
1
I
z
m
O
(
m
V
)
z
(
m
V
)
m
mV
mV
r
Рис. 16.1
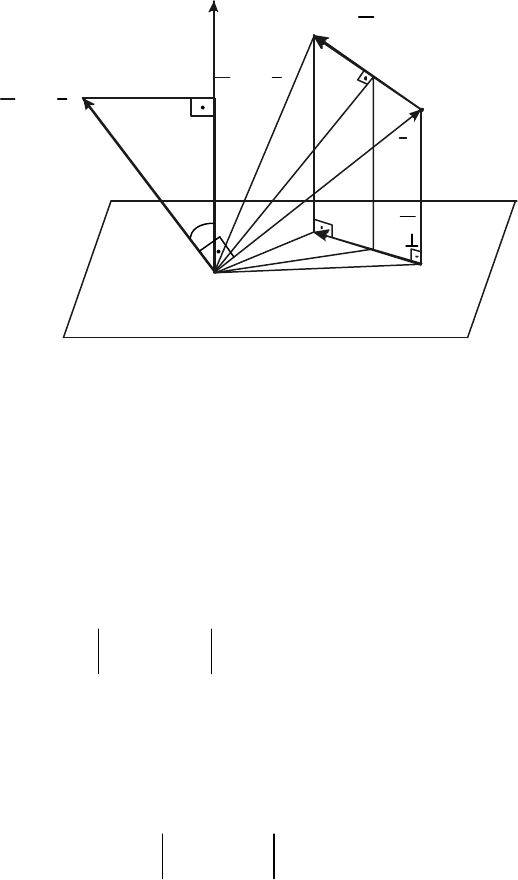
Вектор
)(m
O
Vm
направлен перпендикулярно плоскости, проходящей
через вектор количества движения точки
Vm
и центр О в ту сторону, откуда
поворот под действием вектора
Vm
вокруг центра О виден происходящим
в этой плоскости против хода часовой стрелки (рис. 16.1).
Модуль вектора
)(m
O
Vm
равен
m( )
O
mV mV h
r
r
, (16.2)
где h
плечо вектора
Vm
относительно центра О.
Момент количества движения материальной точки относительно оси
Оz равен проекции вектора
)(m
O
Vm
на эту ось:
m( ) m( )cos
γ
ZO
mV mV
rr
r
, (16.3)
где
γ
угол между вектором
m( )
O
mV
r
r
и осью Оz (рис. 16.1).
Из сравнения формул (16.1)(16.3) с формулами (6.1), (6.2) и (8.1)
следует, что моменты
m( )
O
mV
r
r
и
m( )
Z
mV
r
количества движения
материальной точки определяются аналогично моментам силы
F
)(m F
O
и
