Валькова Т.А. и др. Теоретическая механика
Подождите немного. Документ загружается.

111
, , m ( )
nnn
ее e
C кх C кy ССi
ккi
M
xFMyFI F
r
&&
&&&&
. (19.6)
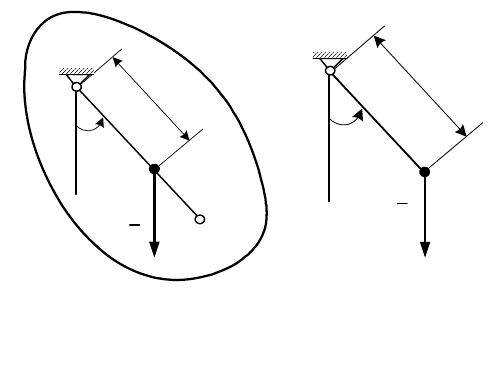
Физический маятник
Физическим маятником называется твердое тело, которое может
совершать колебания вокруг неподвижной горизонтальной оси под
действием силы тяжести
(рис. 19.3, а).
Положение физического маятника в произвольный момент времени
будем определять углом поворота
, отсчитываемом против хода часовой
стрелки от вертикали до прямой
ОС, соединяющей точку О подвеса тела
и его центр масс
С. Заданы: вес Р маятника, расстояние ОС и момент
инерции
O
I
маятника относительно горизонтальной оси подвеса О.
Запишем
дифференциальное уравнение
вращательного движения (19.4),
учитывая, что для маятника
Mm() sin
e
zO
PPa
r
(знак момента отрицательный,
поскольку он направлен
противоположно отсчету угла
)
sin
O
IPa
&&
. (19.7)
Деля обе части (19.7) и введя обозначение
2
/
O
kPaI
, получим
дифференциальное уравнение колебаний маятника
2
sin 0k
&&
(19.8)
Так как это уравнение в элементарных функциях не интегрируется, то
ограничимся рассмотрением только малых колебаний маятника, для которых
sin
. Тогда уравнение (19.8) принимает вид
2
0k
&&
. (19.9)
По структуре уравнение (19.9) совпадает с дифференциальным уравнением
свободных прямолинейных колебаний материальной точки (11.3) и поэтому
его общее решение имеет вид
12
cos sinCktCkt
. (19.10)
O
C
a
K
P
O
C
l
P
а б
Рис. 19.3

Пусть в начальный момент времени t = 0 маятник отклонен на малый угол
0
(0)
и отпущен без начальной скорости
0
(0) 0
&
, тогда постоянные
интегрирования равны:
10
C
,
2
0C
. При данных начальных условиях
движения закон малых колебаний маятника будет
0
coskt
. (19.11)
Следовательно, малые колебания маятника являются гармоническими.
Период этих колебаний физического маятника определяется по
формуле
ф
2
2
O
I
T
kPa
. (19.12)
Из (19.12) следует, что период малых колебаний от угла начального
отклонения
0
не зависит. Этот результат является приближенным. Если
проинтегрировать исходное дифференциальное уравнение (19.8) в
специальных функциях, то можно установить приближенную зависимость
ф
T
от угла
0
, которая будет иметь вид
2
0
ф
21
16
O
I
T
Pa
.
Отсюда вытекает, что при
0
0, 4
рад (около
o
23
) формула (19.12)
определяет период физического маятника с точностью до 1 %.
Один из экспериментальных методов определения моментов инерции
(
метод маятниковых колебаний) основан на использовании формулы
периода малых колебаний физического маятника (19.12). Зная вес
Р тела,
расстояние
ОС = а и измеряя период малых колебаний
ф
T
тела, можно найти
для него момент инерции относительно оси подвеса
О по формуле
22
ф
/(4 )
O
IPaT
.
Полученные результаты охватывают и случай так называемого
математического маятника
материальной точки, подвешенной на
невесомой нерастяжимой нити длиной l
(рис. 19.3, б). Для него
aOCl
,
22
/
O
I
ml P g l
. Подставляя эти величины в (19.12) определим период
малых колебаний математического маятника
м
2/Tlg
. (19.13)
Сопоставляя (19.13) с (19.12) находим, что при длине математического
маятника
пр
//
OO
lIgPaIma
(19.14)
период его колебаний совпадает с периодом колебаний соответствующего
физического маятника.
Длина
пр
l
математического маятника, период колебаний которого равен
периоду колебаний данного физического маятника, называется
приведенной
длиной физического маятника
. Точка K, отстающая от оси подвеса на
расстояние
пр
OK l
, называется центром качаний физического маятника
(рис. 19.3,
а).
Замечая, что по теореме Гюйгенса-Штейнера
2
O С
I
Ima
, запишем
(19.14) в виде
пр
/
C
laIma
. (19.15)
Отсюда следует, что расстояние
пр
OK l
всегда больше расстояния
OC a
,
т. е. центр качаний физического маятника
точка
K
всегда находится ниже
его центра масс
С.
Из формулы (19.15) имеем, что
пр
/
C
K
Cl aIma
. Поэтому, если по-
местить ось подвеса физического маятника в точке
K, то приведенная длина
пр 2
l
полученного маятника согласно (19.15) равна
пр 2 пр
/( ) /( )
CC
lKCImKCImaal
.
Следовательно, точки
K и О являются взаимными, т. е. если ось подвеса
будет проходить через точку
K, то центром качаний будет точка О, и период
колебаний физического маятника не изменится. Это свойство используется
оборотном маятнике, служащем для определения ускорения силы тяжести.
ЛЕКЦИЯ 20
ПРИНЦИП ДАЛАМБЕРА
Принцип Даламбера для материальной точки
Рассмотрим несвободную материальную точку массой m, движущуюся
относительно инерциальной системы отсчета с ускорением
a
. Запишем для
нее основной закон динамики (10.4):
ma F N
rr
r
, (20.1)
где
F
и
N
соответственно равнодействующие активных сил и реакций
связей, приложенных к точке.
Введем силу инерции для материальной точки:
am
Ф
. (20.2)
Отрицательный знак в (20.2) означает, что сила инерции
Ф
направляется
противоположно вектору ускорения
a
.
С учетом (20.2) основной закон динамики (20.1) запишем в форме
равновесия сил:
0 amNF
или
0Ф
NF
. (20.3)
Уравнение (20.3) выражает принцип Даламбера для материальной точки:
в каждый момент движения геометрическая сумма всех приложенных
к материальной точке активных сил, реакций связей и силы инерции равна
нулю.
Принцип Даламбера для механической сиcтемы
Рассмотрим механическую систему, состоящую из n точек. Для к-й
точки системы с массой
к
m
, движущейся под действием равнодействующей
внешних сил
е
к
F
и равнодействующей внутренних сил
i
к
F
, так как
кк
i
к
е
к
NFFF
, то уравнение (20.3) принимает вид
Ф 0
е i
кк к
FF
rrr
. (20.4)
где
Ф
ккк
ma
r
r
. Таким образом, для каждой материальной точки силы
,
е i
кк
FF
rr
и
Ф
к
r
образуют уравновешенную систему сил, и, следовательно,
система этих сил, приложенных к рассматриваемой системе
n точек, также
будет уравновешенной.
Уравнение (20.4) представляет
принцип Даламбера для
механической системы
: если в любой момент времени к каждой из точек
системы кроме действующих на нее внешних и внутренних сил
присоединить соответствующие силы инерции, то полученная система сил
будет уравновешенной, и к ней можно применять все уравнения статики.
Воспользуемся теоремой Пуансо и приведем эту уравновешенную
систему сил к произвольному центру
О. Из статики известно, что для
произвольной системы сил, находящейся в равновесии, ее главный вектор и
главный момент относительно любого центра
О должны быть равны нулю.
Поэтому условия равновесия (6.17) для системы внешних, внутренних сил и
сил инерции материальных точек принимают вид
1
1
Ф 0 ,
m( ) m( ) m(Ф )0 ,
n
е i
кк к
к
n
е i
O к O к O к
к
FF
FF
rrr
rrr
rrr
или
111
111
Ф 0 ,
m( ) m( ) m(Ф )0 .
nnn
е i
кк к
ккк
nnn
е i
O к O к O к
ккк
FF
FF
rrr
rrr
rrr
(20.5)
По свойству внутренних сил
1
0
n
i
к
к
F
r
,
1
m ( ) 0
n
i
O к
к
F
r
r
. (20.6)
Введем обозначения:
1
n
ее
к
к
FF
rr
(20.7)
главный вектор внешних сил системы;
1
ФФ
n
к
к
rr
(20.8)
главный вектор сил инерции системы;
1
m( ) M
n
е e
O к O
к
F
rr
r
(20.9)
главный момент внешних сил относительно центра О;
1
m(Ф )M
n
и
O к O
к
rr
r
(20.10)
главный момент сил инерции точек системы относительно центра О.
Тогда с учетом (20.6)
(20.10) система уравнений (20.5) принимает вид
Ф 0 ,
MM0 .
е
e и
O О
F
rr
rr
(20.11)
В проекциях на оси декартовой системы координат векторные
уравнения (20.11) в случае произвольной пространственной системы сил
дадут шесть скалярных уравнений равновесия:
Ф 0 , M M 0 ,
Ф 0 , M M 0 ,
Ф 0 , M M 0 .
е e и
xx xx
е e и
yy yy
е e и
zz zz
F
F
F
(20.12)
Для практического применения принципа Даламбера необходимо
уметь вычислять главный вектор
Ф
r
и главный момент
M
и
O
r
сил инерции то-
чек системы. Из первого уравнения системы (20.11) имеем
1
Ф .
n
ее
к
к
FF
rr r
Согласно теореме о движении центра масс системы (15.5)
1
n
е
к C
к
FM a
r
r
, где
М масса системы;
C
a
ускорение ее центра масс С относительно
инерциальной системы отсчета. Тогда
Ф .
C
M
a
r
r
(20.13)
Главный вектор сил инерции механической системы (твердого тела)
равен произведению массы системы (тела) на ускорение центра масс и
направлен противоположно этому ускорению.
Поскольку вектор
е
F
приложен в центре приведения О, то из первого
уравнения (20.11) следует, что и главный вектор сил инерции
Ф
r
также
приложен в центре
О.
Если центр масс точка
С движется по криволинейной траектории, то
n
ССC
aa a
rrr
, где
a
n
С
и
C
a
соответственно нормальное и касательное
ускорения этой точки.
Поэтому главный вектор сил инерции
Ф
r
следует в точке О разложить
на нормальную и касательную составляющие:
τ
Ф ФФ ,
n
rrr
где
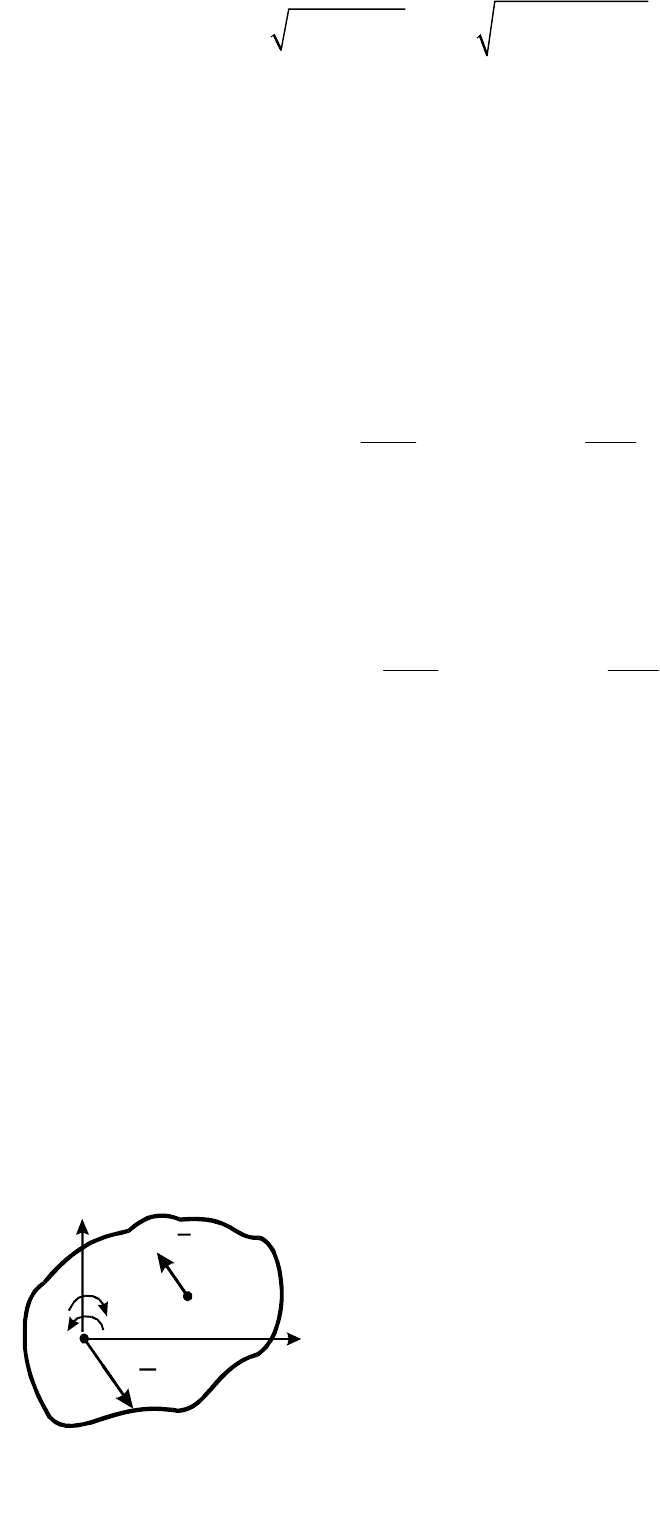
τ
τ
22
22 τ
Ф , Ф ,
ФФФ .
n
nC C
n
nCC
M a M a
Ma a
rr
rr
(20.14)
Главный вектор сил инерции механической системы (твердого тела) от
выбора центра приведения не зависит
.
Из второго уравнения системы (20.11) и шестого уравнения системы
(20.12) имеем
M M , M M .
и e и e
О Ozz
rr
Согласно теоремам об изменении кинетического момента для механической
системы (16.14), (16.15)
M , M ,
ee
Oz
Oz
dK dK
dt dt
r
r
где
O
K
и
z
K
кинетические моменты механической системы соответственно
относительно центра
О и оси Oz. Тогда
, .
ии
Oz
Oz
dK dK
MM
dt dt
r
r
(19.15)
Главный момент сил инерции механической системы (твердого тела)
относительно центра О или оси
Oz равен взятой с противоположным
знаком производной по времени от кинетического момента системы (тела)
относительно того же центра или оси.
Главный момент сил инерции механической системы (твердого тела)
зависит от выбора центра приведения О.
Приведение сил инерции твердого тела
Воспользовавшись теоремой Пуансо, рассмотрим приведение сил
инерции точек твердого тела к центру
О при различных видах его движения.
1.
Поступательное движение. При поступательном движении силы
инерции точек тела образуют систему
параллельных сил, которая всегда приводятся к
равнодействующей
Ф
C
M
a
r
r
, приложенной
в центре масс тела.
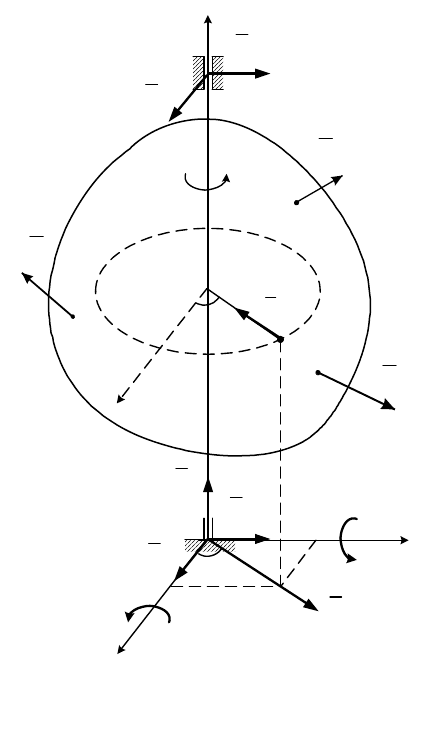
2.
Вращательное движение. Если тело
имеет плоскость материальной симметрии
Оху и
вращается вокруг неподвижной оси
Оz,
О
x
y
C
a
C
Ф
М
и
z
Рис. 20. 1

перпендикулярной этой плоскости, то при приведении сил инерции точек
тела к центру
О они заменяются главным вектором
Ф
C
M
a
r
r
,
приложенным в центре
О, и парой сил с моментом
M
и
z
, лежащей в плоскости
симметрии
Оху (на рис. 20.1 изображено сечение тела плоскостью Оху).
Поскольку для вращающегося тела согласно (16.9)
ω
zz
KI
, то
ω
M ε .
и
z
zzz
dK d
II
dt dt
(20. 16)
Знак «
» в (20.16) показывает, что момент сил инерции
M
и
z
на рис. 20.1
направляется противоположно угловому ускорению
ε
тела.
В случае когда ось вращения
z проходит через центра масс С тела
перпендикулярно плоскости материальной симметрии
ху, поскольку
0
C
a
,
то силы инерции точек тела приводятся только к паре, лежащей в плоскости
симметрии тела с моментом
и
Сz
M
, определяемом согласно (19.16):
M ε .
и
Сz Сz
I
(20.17)
3.
Плоскопараллельное движение. При плоскопараллельном
движении тела, имеющего плоскость материальной симметрии
Оху и
движущегося параллельно этой плоскости, силы инерции точек тела
приводятся к результирующей силе
Ф
,
приложенной в центре масс
С тела и к
паре с моментом
и
Сz
M
, лежащей в
плоскости симметрии тела. При этом
Ф ,
M ε .
C
и
Сz Сz
M a
I
r
r
(20.18)
Динамические реакции
подшипников
при вращении тела вокруг оси
Рассмотрим твердое тело, равномерно вращающееся с угловой
скоростью
вокруг оси, закрепленной в подшипниках А и В (рис. 20.3).
Свяжем с телом вращающуюся вместе с ним декартовую систему
координат
Ахуz, по отношению к которой координаты центра масс и
моменты инерции тела будут постоянными величинами.
C
x
y
C
a
Ф
О
M
C
z
Рис 20
2
Пусть на тело действуют активные силы
12
, ,...,
ee e
n
FF F
rr r
. Обозначим
проекции главного вектора
e
F
r
этих сил на оси Ахуz через
, ,
еее
x
yz
FFF
, а их
главные моменты относительно тех же осей
через
M, M, M
eee
x
yz
при этом,
поскольку
ω = const
, то
M0
e
z
.
Для определения динамических
реакций
, , , ,
A
AABB
X
YZXY
rrrrr
подшипников, т. е. реакций
возникающих при вращении тела,
согласно принципу Даламбера
присоединим ко всем активным силам и
реакциям связей силы инерции
Ф
к
r
(к =
1, 2, …,
n) всех частиц тела, приведя их
к центру
А.
Тогда силы инерции приводятся
к главному вектору
Ф
, приложенному
в точке
А, и к паре сил с моментом
1
Mm(Ф )
n
и
AAк
к
rr
r
. Проекции этого
вектора на оси х и у будут:
1
1
Mm(Ф ),
Mm(Ф ),
M0.
n
и
xxк
к
n
и
yyк
к
и
z
r
r
так как
ω = const
. Поскольку в каждый момент движения на тело действует
уравновешенная система сил (активных, реакций связей и сил инерции), то
запишем систему уравнений равновесия (20.12), полагая
АВ = b:
Ф 0,
Ф 0,
Ф 0,
MM0,
MM0,
MM0.
е
ABx x
е
AB y y
е
Az z
e и
Bxx
e и
Byy
e и
zz
XXF
YY F
ZF
Yb
Xb
(20.19)
y
x
'
z
B
X
A
Y
A
Z
A
A
O
C
x
C
y
C
Y
B
X
B
Ф
y
M
и
x
M
и
x
C
a
n
C
h
1
F
e
2
F
e
n
F
e
Рис. 20.3
Последние уравнение
MM0
e и
zz
в (20.19) обращается в тождество,
поскольку
M0
e
z
и
M0
и
z
.
Согласно (20.13) главный вектор сил инерции
Ф
C
m a
r
r
, где
m
масса тела. При
ω = const
центр масс С имеет только нормальное ускорение
2n
СС C
aa h
, где
C
h
расстояние от точки С до оси вращения z.
Следовательно, направление вектора
Ф
r
совпадает с направлением ОС.
Вычисляя проекции
Ф
r
на координатные оси и учитывая, что
cos , sin
CCCC
hxhy
, где
,
CC
x
y
координаты центра масс, найдем:
22
22
Фωcosαω,
Фωsin αω,
Ф 0.
x
CC
yC C
z
mh mx
mh my
Чтобы определить
M, M,
ии
x
y
рассмотрим какую-нибудь частицу
(, ,)
кккк
Bxyz
тела с массой
к
m
, отстающую от оси на расстояние
к
h
. Для нее
при
ω = const
сила инерции имеет только нормальную составляющую
2
Фω
n
ккк
mh
, проекции которой, как и вектора
Ф
r
, равны:
22
Фω; Фω; Ф 0.
кx кк кy ккz
mx my
Тогда получаем:
2
2
m(Ф ) Фω;
m(Ф ) Фω.
x ккy кккк
y ккx кккк
zmyz
zmxz
r
r
Составляя такие выражения для всех точек системы, складывая их и вынося
общий множитель за скобки, придем к равенствам:
22
1
22
1
M ωω;
M ωω;
n
и
x ккк yz
к
n
и
y ккк xz
к
myz I
mxz I
где
,
xz yz
I
I
соответствующие центробежные моменты инерции тела.
Подставляя все найденные значения в (20.19), получим
