Валькова Т.А. и др. Теоретическая механика

Подождите немного. Документ загружается.

ω ;

;

M ω ;

M ω .

AB x C

AB y C

Byxz

Bxyz

XX Fmx

YY F my

Xb I

Yb I







 









 







(20.20)

Уравнения (20.20) определяют динамические реакции, действующие на

ось равномерно вращающегося твердого тела, если осью вращения является

ось

Назовем

статическими реакциями те значения реакций, которые дают

уравнения (20.20), если в них положить

ω = 0

. Как видно, из уравнений

(20.20), динамические реакции могут вообще быть значительно больше

статических, причем это зависит не только от значения

, но и от величин

, , ,

C C xz yz

yI I

, характеризующим распределение масс тела относительно оси

вращения

Однако из уравнений (20.20) следует, что наличие вращения не будет

влиять на значения реакций подшипников

А и В, если

0, 0;



(20.21)

0, 0.

xz yz



(20.22)

Равенства (20.21) и (20.22) выражают условия динамической уравновешен-

ности

тела, вращающегося вокруг оси z, т. е. условия равенства

динамических реакций, действующих на ось вращающегося тела,

статическим реакциям

Условия (20.21) означают, что центр масс тела должен лежать на оси

вращения, а условия (20.22)



что ось вращения должна быть главной осью

инерции тела для начала координат

А. При одновременном же выполнении

условий (20.21) и (20.22) ось

Az будет главной центральной осью инерции

тела.

Следовательно,

динамические реакции, действующие на ось

вращающего тела, будут равны статическим, если

ось вращения является

одной из главных центральных осей инерции тела. Этот вывод остается

справедливым и в случае, если тело вращается неравномерно.

Данная задача позволяет уяснить механический смысл величин

, а именно: центробежные моменты инерции

характеризуют

степень динамической неуравновешенности тела при его вращении вокруг

оси z.

Динамическое уравновешивание вращающихся тел представляет собой

важную техническую задачу, которая, как было показано, сводится к

определению главных центральных осей инерции тела. Отметим, что любое

тело имеет, по крайней мере, три взаимно перпендикулярные главные

центральные оси инерции.

Докажем важное положение:

любую ось, проведенную в теле, можно

сделать главной центральной осью инерции прибавлением двух точечных

масс.

Пусть для тела массой m величины

, , ,

C C xz yz

yI I

известны и не равны

нулю. Прибавим к телу две массы

в точках

1111

(, ,)Bxyz

2222

(, ,)Bxyz

соответственно. Тогда из формул (14.9) и (14.25) следует, что

если удовлетворить равенствам

11 2 2 11 2 2

111 222 111 2 22

0, 0,

xz yz

mx m x m x my m y m y

Imxzmxz Imyzmyz

   

(20.23)

то для полученного тела будет

CC xzyz

xy II











, т. е. ось z станет

главной центральной осью инерции.

Подбирая массы

и их положения так, чтобы удовлетворялись

уравнения (20.23), можно решить поставленную задачу. Частью величин при

этом следует, конечно, задаться изначально (например, можно задать

значения

, но так чтобы



, а

112 2

, , ,

yxy

найти из

уравнений (20.23)).

Такой метод уравновешивания вращающихся тел широко используется

в технике для уравновешивания коленчатых валов, кривошипов, спарников и

т. п. При этом окончательная балансировка производится на специальных

стендах.

ЛЕКЦИЯ 21

ПРИНЦИПЫ АНАЛИТИЧЕСКОЙ МЕХАНИКИ

Классификация связей

В аналитической механике рассматриваются наиболее общие методы

изучения равновесия и движения материальных систем. Объектом

исследования в аналитической механике является система материальных

точек или тел.

Система материальных точек называется

свободной, если положения

отдельных ее точек и их скорости могут принимать произвольные значения.

Материальная система называется несвободной, если вследствие каких-

либо ограничений (связей) точки системы не могут занять произвольного

положения в пространстве и иметь произвольные скорости.

Аналитически связи выражаются уравнениями или неравенствами, т. е.

соотношениями между радиус-векторами точек системы, их скоростями

и временем.

Связи, выраженные уравнениями, называются

удерживающими, связи

выраженные неравенствами

 неудерживающими.

Для материальной системы, состоящей из

n точек, наложенные на нее k

удерживающие связи можно в общем случае записать системой уравнений

вида

νννννν

(, ,, , ,,) 0,(ν 1, 2,..., ), ( 1, 2, ..., )

x y z x y z t n j k





, (21.1)

где



 соответственно проекции радиус-вектора

и скорости

-й точки на оси декартовой системы координат.

Если уравнения связей (19.1) содержат явно время

t, то связь

называется

нестационарной. Например, связь, наложенная на материальную

точку, выраженная уравнением

222 2

(5)

tyz R

является нестационарной. В этом случае точка в процессе движения остается

на поверхности сферы радиусом

R, центр которой перемещается по оси Ox.

Если уравнение связи не содержит явно время

t, то связь называется

стационарной. Например, связь будет стационарной для двух материальных

точек, соединенных невесомым стержнем длиной



222

21 2 1 21

(()().

xyyzzL

Здесь

, y

, z

, x

, y

, z

– декартовые координаты материальных точек.

Если связи материальной системы являются стационарными, то

система называется

склярономной, если связи нестационарные, то система 

реономной.

Связь, накладывающая ограничение только на координаты точек

системы, называется

геометрической или голономной. Уравнения связей в

этом случае имеют вид:

ννν

( , , , ) 0, (ν 1, 2, ..., ), ( 1, 2, ..., )

xyzt n j k 

. (21.2.)

Во всех приведенных выше примерах связи являлись голономными.

Связь называется неголономной (кинематической), если уравнения

связи (21.1) содержат неинтегрируемым образом производные от координат

по времени или дифференциалы

координат.

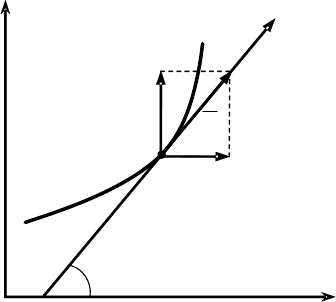
Например, при движении конька

по поверхности льда для отсутствия

соскальзывания необходимо, чтобы

скорость

центра тяжести C конька

была бы направлена вдоль его оси (рис.

21.1), т. е. по касательной к траектории в

точке

C. Тогда

cos ,

sin ,









или уравнение неголономной связи

имеет вид

tg 0.





Материальная система, на которую наложены голономные связи,

называется

голономной, а материальная система с неголономными связями –

неголономной.

В дальнейшем будут рассматриваться только голономные системы.

Числом степеней свободы голономной материальной системы

называется число

S независимых параметров (координат), полностью

определяющих ее положение совместимое с наложенными на неё связями.

Если на материальную систему, состоящую из

n точек, наложено k

голономных связей, то это значит, что не все декартовые координаты точек

системы независимы друг от друга. Действительно, независимыми являются

только

3nk

координат, так как k координат можно выразить через

остальные

3nk



координат с помощью уравнений связей (20.2).

Следовательно, число степеней свободы для рассматриваемой системы равно

3.Snk





(21.3)

Возможные перемещения. Возможная работа

Введем понятия действительного и возможного перемещений на

примере одной материальной точки







, подчиненной одной голономной

связи

(1)j 

( , , , ) 0fxyzt



. (21.4)

Действительным перемещением



точки называется бесконечно

малое перемещение этой точки под действием активных сил и реакций связи.

Действительное перемещение

происходит за время

в соответствии с

дифференциальным уравнением движения точки и уравнением связи (21.4).







Рис. 21.1

Дифференциальное уравнение в частных производных, которому

подчинено действительное перемещение точки

dr dx i dy j dz k

, в

положении

0000

(, ,)

xyz

получим, вычислив дифференциал от левой части

уравнения (21.4) и приравняв его к нулю:

0000

ffff

df dx dу dz dt

xxxt









   







. (21.5)

Возможным перемещением

δr

называется воображаемое бесконечно

малое перемещение точки, допускаемое связью в фиксированный момент

времени. Возможное перемещение не обладает длительностью и не

происходит под действием сил.

Дифференциальное уравнение в частных производных, которому

подчинены возможные перемещения точки

δδ δ δ rxi yjzk

в положении

0000

(, ,)

xyz

, получим, вычислив дифференциал левой части уравнения

(21.4) при фиксированном времени, т. е. определив изохронную вариацию

функции

( , , , ),

xyzt

и приравняв ее к нулю:

δ δ δ δ 0

fff

fxу z

xyz













 















, (21.6)

Из сравнения (21.6) и (21.5) видно, что возможное перемещение совпадает

с действительным перемещением точки только в случае стационарных

связей, когда

t

Вводя вектор-градиент функции (21.4) при фиксированном времени

000

fff

ijk

х yz

  



  

  



  

можно условие (21.6) записать в форме скалярного произведения векторов

f



δr

δ 0fr





Следовательно, виртуальные перемещения

δr

точки представляют со-

бой векторы, расположенные в касательной плоскости, проведенной в той

точки

поверхности, определяемой уравнением (21.4), в которой в данный

момент времени находится материальная точка. При стационарной связи

действительное перемещение



совпадает в фиксированный момент

времени с одним из виртуальных перемещений

δr

. Так как

dr V dt

, то при

стационарной связи вектор

δr

направляется также как вектор скорости

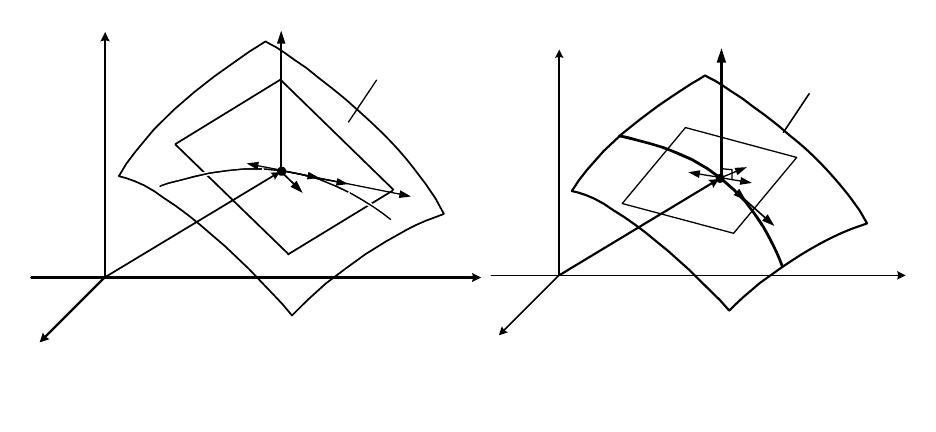
точки в данный момент времени. При нестационарной связи вектор

действительного перемещения

точки в положении

не совпадает ни

с одном их векторов ее возможных перемещений

δr

(рис. 21.2, б).

Рассмотрим систему, состоящую из n материальных точек,

подчиненных голономным связям (21.2).

Возможными перемещениями точек системы называется

совокупность бесконечно малых векторов:

νν ν ν

δδ δ δ r

i у jzk

(

1, 2, . . . , )n



, (21.7)

удовлетворяющих системе уравнений

νν

ν 1

δ 0, ( 1, 2, ..., ).

rj k



 



(21.8)

Количество независимых виртуальных перемещений системы равно

числу

S ее степеней свобод.

Пусть в фиксированный момент времени на каждую

-ю

материальную точку системы действует сила

(

1, 2, , ).

... n







(

x, y, z

) = 0





(

x, y, z, t

) = 0



а б

Рис. 21.2

Возможной работой называется элементарная работа сил

, , ...,

FF F

rr r

на возможных перемещениях

δ , δ , ..., δ

rr r

точек системы:

11 2 2

ν 1

δδδ... δδ

FrFr F r Fr



   



rr r r

. (21.9)

В декартовой системе координат

νν ν ν

Fi F j Fk

rrv



ννννν

ν 1

δδδδ

xyz

Fх F у Fz







. (21.10)

Связи, для которых возможная работа реакций





связей на любом

возможном перемещении системы равна нулю:

νν

ν 1

δ 0,









(21.11)

называются

идеальными.

Для одной материальной точки, движущейся по поверхности связи

f(x, y, z, t)= 0, условие (21.11) принимает вид

δ 0Nr





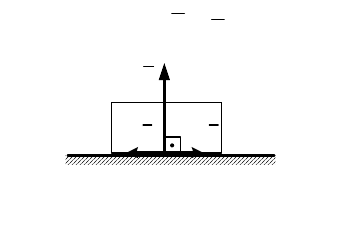
. Следовательно, при

идеальной связи реакция



перпендикулярна

любому возможному перемещению

δr

, т. е.

направлена по нормали к поверхности связи

(например, на рис. 21.3). Поэтому в случае

идеальной связи точка движется по

поверхности связи без трения. Условие (21.11)

является обобщением для случая системы,

состоящей из

n точек. Можно убедиться, что

примерами идеальной связи являются гладкая

поверхность, шарнир без трения, связь при качении без скольжения.

Принцип возможных перемещений

В основе аналитической статики лежит

принцип возможных

перемещений

: необходимым и достаточным условием равновесия

голономной материальной системы, подчиненной идеальным стационарным

связям, является равенство нулю элементарной работы всех активных сил

на любом возможном перемещении точек системы



A = N r =



Рис. 21.3

νν

ν 1

δ δ 0

А Fr







. (21.12)

Под равновесием понимается такое состояние системы, при котором

все ее точки под действием приложенных активных сил и реакций связей

находятся в покое по отношению к инерциальной системе отсчета, т. е.

ν 0



(

1, 2, ..., )n

Докажем

необходимость условия (21.12). Пусть материальная система,

состоящая из

n точек, на которую наложены k голономных идеальных

стационарных связей, находится в положении равновесия. Тогда на каждую

точку системы действует уравновешенная система сил:

νν





(

1, 2, . . . , )n



, (21.13)

где

– равнодействующие активных сил и реакций связей,

действующих на

-ю точку системы.

Сообщим точкам системы возможные перемещения

δ , δ , ..., δ

rr r

Умножим скалярно каждое уравнение (21.13) на соответствующий вектор

возможного перемещения

δr

ννν

()δ 0FN r



1, 2, . . . , )n

. (21.14)

Сложив n уравнений (20.14), получим

ννν

ν 1

()δ 0









или

νν νν

ν 1 ν 1

δδ0

rNr









. (21.15)

Так как связи, наложенные на систему, идеальные, то согласно (21.11) вторая

сумма в (21.15) равна нулю. Следовательно,

νν

ν 1

δ δ 0

А Fr







что и требовалось доказать.

Докажем

достаточность условия (21.12). Допустим обратное, что при

выполнении условия (21.12) система начнет движение из состояния покоя,

т. е. ее точки испытают действительные перемещения

(

1, 2, ..., )n

а действующие на систему активные силы и реакции связей совершат на этих

перемещениях работу. По теореме об изменении кинетической энергии

имеем



νν

ν 1 ν 1

dT dA F N dr









. (21.16)

Поскольку система начинает движение из состояния покоя, то 0d

поэтому из (21.16) получаем



ννν

ν 1

FNdr









. (21.17)

При стационарных связях действительные перемещения

точек системы

в фиксированный момент времени совпадают с их виртуальными

перемещениями

δr

т. е.

νν

δ .dr r



Тогда (21.17) принимает вид



ννν

ν 1

δ 0

FN r









или

νν νν

ν 1 ν 1

δδ0 .

rNr



  



Так как связи идеальные, то

νν

ν 1

δ 0.









Поэтому

δ ,

νν

ν 1

Fr 0







что противоречит исходному условию (21.12).

Следовательно, предположение о движении неверно, и система при выпол-

нении условия (21.12) находится в равновесии, что и требовалось доказать.

Пользуясь принципом виртуальных перемещений, можно:

1) определять положения равновесия несвободной материальной системы,

2) находить соотношения между активными силами при равновесии системы,

3) определять реакции связей наложенных на систему в положении

ее равновесия.

Общее уравнение динамики

Рассмотрим голономную систему n материальных точек, подчиненную

идеальным стационарным связям. Для получения общего уравнения

динамики рассмотрим произвольную

-ю точку системы и запишем для нее

принцип Даламбера (20.3):

ννν

Ф 0 (ν 1,2, ..., )F N n  

rrr

. (21.18)

В любой момент движения геометрическая сумма всех приложенных

к точке активных сил, реакций связей и силы инерции равна нулю

В (21.18) сила инерции

-й точки

ννν

Ф (ν 1,2, ..., )ma n 

Мысленно зафиксируем время

t и сообщим точкам системы возможные

перемещения

δ , δ , ..., δ

rr r

соответственно. Скалярно умножим каждое

уравнение (21.18) на соответствующий вектор возможного перемещения

δ r



и сложив найденные

n уравнений, получим:



ννν ν

ν 1

Фδ0

FN r









uuur

rr r

или



νν νν

ν 1 ν 1

Фδ δ 0

F r N r







 



uuuruuur

rr r

. (21.19)

По свойству идеальных связей (21.11)

νν

ν 1

δ 0

N r









uuur

. Следовательно,

с учетом (21.11) уравнение (21.19) принимает вид



ννν

ν 1

Фδ 0.









(21.20)

Равенство (21.20) называется

общим уравнением динамики: в

каждый момент движения голономной системы, подчиненной идеальным

стационарным связям, элементарная работа активных сил и сил инерции на

возможном перемещении системы равна нулю.

В декартовых координатах

νν ν ν

FFiFjFk

νν ν ν νν

Ф mxi my j mzk  

&&&&

ννν

δδ δ δrxiyjzk

uur

где

kji



, ,

– орты соответствующих декартовых осей. Уравнение (21.20)

можно записать в виде



νννννννννννν

ν 1

δδδ0.

xy z

Fmx x Fmy y Fmz z











&&&&

(21.21)