Валькова Т.А. и др. Теоретическая механика

Подождите немного. Документ загружается.

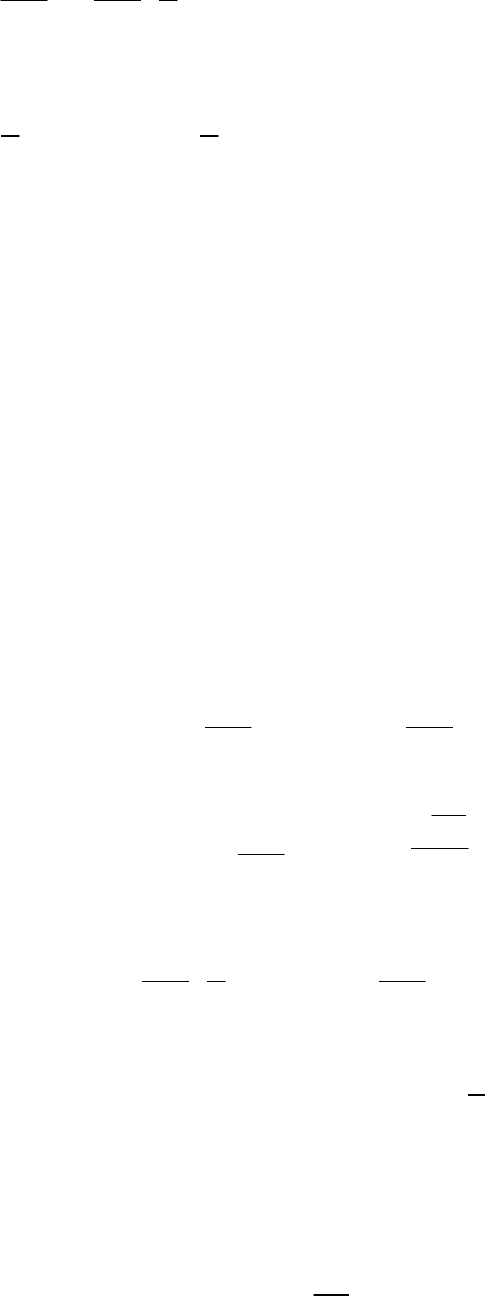
Тогда обобщенная потенциальная сила равна

11 11 1

П 1

= =

= δδ ( 1, 2, ..., ),

mijij

SS SS S

ij mi j ij mj i mj j

ij ij j

Qcqq

cq cq cq m s



  







 















  

(24.12)

где использовалось (24.7) и свойство симметрии обобщенных

коэффициентов жесткости

ij ji



Рассмотрим определение обобщенной силы сопротивления

. Пусть

на точки механической системы действуют силы линейно-вязкого

сопротивления, т. е. сопротивления пропорционального первым степеням их

скоростей:

( 1, 2, ..., )

ккк

RbV к n 

, (24.13)

что соответствует малым скоростям.

Согласно определению (23.4) для обобщенной силы найдем выражение

для обобщенной силы сопротивления

= =

= ,

кк

m ккк

кк

QF bV







 

































(24.14)

где введена диссипативная функция Рэлея

кк

RbV





Для склярономной системы в потенциальном стационарном поле

диссипативная функция Рэлея может быть выражена через полную энергию

Е = Т + П механической системы в виде равенства





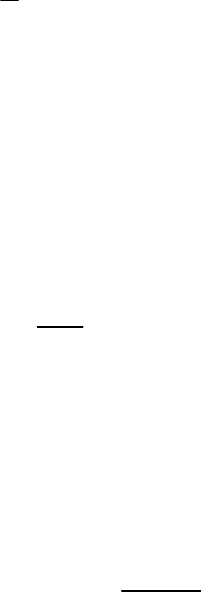
которое означает, что удвоенная функция Рэлея равна скорости убывания

полной энергии в диссипативной системе

По аналогии с кинетической энергией

Т системы выразив функцию

Рэлея

R через обобщенные скорости, разложив ее в ряд в окрестности

положения равновесия и отбросив члены выше второго порядка малости,

получим



ij i j

Rbqq







. (24.15)

Постоянные коэффициенты





называются приведенными

коэффициентами сопротивления

, которые ниже будем обозначать

Подставляя (24.15) в (24.14), получим выражение для обобщенной

силы сопротивления

, входящее в линеаризованное уравнение Лагранжа

(24.1), аналогичное (24.6)

mmjj

Qbq





 





. (24.16)

Важную категорию образуют возмущающие силы



внешнего

происхождения, описываемые заданными функциями времени и не

зависящие от движения системы.

Обобщенная возмущающая сила

()

определяется по формуле

δ ()

()



, (24.17)

где

δ ()



возможная работа возмущающих сил системы на возможном

перемещении системы при

δ 0

q 

В этом параграфе при определении обобщенных возмущающих сил

()

ограничимся случаем, когда на механическую систему действуют

только гармонические возмущения. Тогда обобщенные возмущающие силы

изменяются во времени по закону

() sin( δ ) ( 1, 2, ..., )

mm m

Qt H pt m s 

(24.18)

т. е. силы

()

имеют одинаковые частоты р, но различные достаточно

малые амплитуды

и начальные фазы

С учетом (24.8), (24.9), (24.12), (24.16) и (24.18) линеаризованное

уравнение Лагранжа (24.1) принимает вид

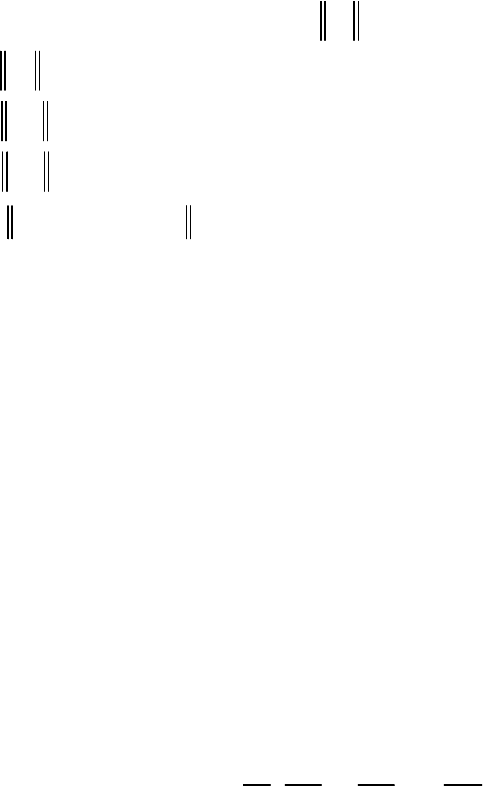
111

sin( δ ) ( 1, 2, ..., )

SSS

mj j mj j mj j m m

jjj

aq cq bq H pt m s



    



&&&

или



sin( δ ) ( 1, 2, ..., )

mj j mj j mj j m m

aq bq cq H pt m s



   



&&&

. (24.19)

Линейные дифференциальные уравнения с постоянными

коэффициентами (24.19) можно представить в векторно-матричной форме

ˆˆ

qBqCqH





&&&

, (24.20)

где введены обозначения:

qq



вектор-столбец обобщенных координат,

a



квадратная матрица обобщенных коэффициентов инерции,

Bb



квадратная матрица приведенных коэффициентов сопротивления,

Cc



квадратная матрица обобщенных коэффициентов жесткости,

sin( δ )

HH pt



вектор-столбец возмущающих сил.

В зависимости от действующих на механическую систему сил

различают три вида колебательных движений:

собственные (гармонические) колебания, происходящие под

действием только потенциальных (восстанавливающих) сил,

затухающие колебания, происходящие под действием

потенциальных сил и сил линейно-вязкого сопротивления среды,

вынужденные колебания, когда кроме потенциальных сил и сил

сопротивления среды, действуют возмущающие силы, зависящие от времени.

Свободные колебания механической системы

с одной степенью свободы

При изучении данного вида колебаний будем исходить из уравнения

Лагранжа второго рода (24.1), которое при

S = 1 имеет вид

()

dT T

dt q q q







 

. (24.21)

В этом случае кинетическая энергия

Т (24.5) системы определяется

зависимостью

T аq

а потенциальная энергия (24.11)



сq

где а и с  соответственно обобщенная масса системы и обобщенный

коэффициент жесткости.

Обобщенная сила вязкого трения

;







где диссипативная функция рассеяния Рэлея

Rbq

; b  обобщенный

коэффициент вязкости.

Вычислив соответствующие производные, входящие в уравнение

(24.1), получим уравнение (24.19) для

S = 1 и в отсутствии возмущающих

сил:

0aq bq cq





&&&

. (24.22)

Уравнение (24.22) называется дифференциальным уравнением свободных

колебаний при линейно-вязком сопротивлении

Если на механическую систему не действуют силы линейно-вязкого

сопротивления, то уравнение (24.22) соответствует

дифференциальному

уравнению свободных колебаний системы

0aq cq





(24.23)

или

0qkq





где

/kca

 собственная (круговая) частота свободных колебаний

системы. Решение уравнения (24.23) при начальных условиях

(0) ; (0)qqqq

имеет вид:

sin cos .

qktqkt



(24.24)

После несложных преобразований, решение (24.24) можно записать более

наглядной форме:

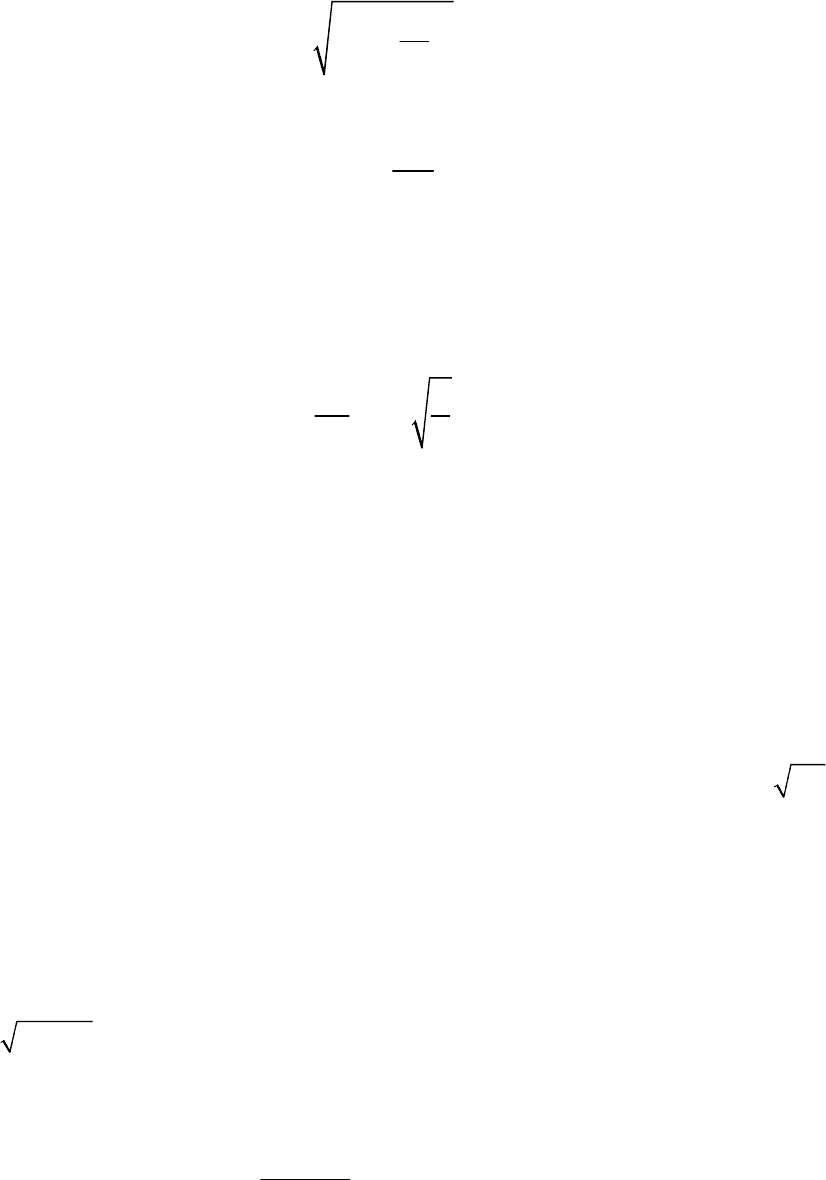
sin( ).qA kt





(24.25)

Здесь амплитуда свободных колебаний

А определяется выражением

();



а начальная фаза колебаний

arctg .



Зависимости (24.24) и (24.25) описывают свободные гармонические

колебания механической системы около положения устойчивого равновесия

Величина

Т, определяемая выражением





является

периодом свободных колебаний.

Теперь вернемся к уравнению (24.22). Разделим его на коэффициент

а,

обозначим отношения

/2, / ba h ca k

и запишем уравнение (24.22) в

форме

20xhxkx

&&&

. (24.26)

В зависимости от соотношений между

k и h общее решение уравнения

(24.26) имеет разный характер. Если сопротивление мало (

k > h), т. е.

значение коэффициента вязкости

b будет удовлетворять условию

2,bac

то механическая система будет совершать затухающие колебания около

положения устойчивого равновесия



. В этом случае решение уравнения

(24.26) следует искать в виде

112 1

(sin cos ),

qe c ktc kt





(24.27)

где

kkh

 круговая частота затухающих колебаний. Постоянные

интегрирования

и с

с учетом начальных условий движения

(0) ,qq



(0)qq

определяются выражениями

120

; .

qhq

ccq





После преобразования решения (24.27) в форму одночлена, получим

sin( ).

qBe kt



 

(24.28)

Колебания, происходящие по закону (24.8), называются затухающими

колебаниями механической системы. Коэффициент В в (24.28) равен

()

qhq







а начальная фаза

arctg .

qk h

qhq













Уравнение (24.28) показывает, что в рассматриваемом случае движение

системы имеет гармонический характер с убывающей во времени по

экспоненциальному закону величиной отклонения от положения равновесия.

Эту величину



называют амплитудой затухающих колебаний.

Количественной мерой быстроты затухания (убывания амплитуды)

колебаний механической системы является логарифмический декремент,

который определяется выражением

22 2

kh acb





  



(24.29)

Для наглядного представления о характере колебаний механической

системы удобно использовать понятие

фазовой плоскости. Фазовая

плоскость представляет собой плоскость, образованную прямоугольной

системой координат, в которой по осям откладываются обобщенная

координата и обобщенная скорость. В этом случае любое состояние

механической системы определяется точкой фазовой плоскости с

координатами (

q, q



), которая называется изображающей точкой. При

движении механической системы эта точка описывает на фазовой плоскости

кривую. Геометрическое место положений изображающей точки на фазовой

плоскости называется

фазовой траекторией.

Совокупность фазовых траекторий для всех возможных случаев

движения системы называется фазовой диаграммой. Для случая свободных

гармонических колебаний системы, ее фазовая траектория имеет форму

эллипса; для затухающих колебаний фазовая траектория представляет собой

логарифмическую спираль, накручивающуюся на начало координат, которое

называется устойчивым фокусом.

ЛЕКЦИЯ 25

Свободные колебания механической системы

с двумя степенями свободы

Уравнения Лагранжа второго рода (24.1) для системы с двумя

степенями свободы, находящейся под действием только потенциальных

(восстанавливающих) сил, запишутся в виде

11 1

22 2

() ;

() .

dT T

dt q q q

dT T

dt q q q

 







 





















(25.1)

Согласно (24.5) и (24.11) кинетическая и потенциальная энергии

системы являются квадратичными формами обобщенных скоростей и

обобщенных координат соответственно и определяются выражениями:

11 1 12 1 2 22 2

П 2.

Taq aqq aq

cq cqq cq

 

&&&&

Здесь коэффициенты а

, а

и с

, с

по-прежнему имеют смысл

обобщенных масс и обобщенных коэффициентов жесткости.

Вычислим производные от кинетической энергии и потенциальной

энергии, входящие в (25.1), и подставим найденные выражения в эти

уравнения. После не сложных преобразований получим уравнения (24.19) в

отсутствие сопротивления и возмущающих сил:

11 1 12 2 11 1 12 2

21 1 22 2 21 1 22 2

aq aq cqcq



  





   





&&&&

(25.2)

Уравнения (25.2) называются дифференциальными уравнениями

свободных колебаний механической системы с двумя степенями свободы

В случае малых колебаний механической системы около положения её

устойчивого состояния равновесия (

0qq



) решение уравнений (25.2)

будем искать в виде

sin( ),

qA kt

qB kt









(25.3)

где А, В  амплитуды колебаний, k  круговая частота колебаний, α 

начальная фаза колебаний являются неизвестными постоянными

величинами.

Подставим решение (25.3) в исходные дифференциальные уравнения

движения (25.2) и сгруппируем слагаемые:

11 11 12 12

21 21 22 22

()()sin()0;

()()sin()0.

с ak A с ak B kt



 





 



В общем случае

sin( ) 0kt





. Следовательно, должны выполняться

равенства:

11 11 12 12

21 21 22 22

()()0;

()()0.

с ak A с ak B

с ak A c ak B















(25.4)

Эти алгебраические линейные однородные уравнения относительно

А и В

должны иметь ненулевое решение (

0qq



соответствует покою, а не

движению). Поэтому определитель системы (25.4) должен равняться нулю:

11 11 12 12

21 21 22 22

cakcak







Раскрывая его, получим

22 22

11 11 22 22 12 12

()( )()0.cakc ak cak

(25.5)

Уравнение (25.5) называется

уравнением частот, или вековым уравнением.

Корни

этого уравнения вещественные и положительные. Это

доказывается математически, но может быть обосновано и тем, что если

kk

не будут вещественными, то система дифференциальных

уравнений (25.2) не будет иметь решения вида (25.3), что для механической

системы, находящейся в положении устойчивого равновесия не возможно,

так как после малых возмущений она должна двигаться около положения

0qq

Каждому корню

будет отвечать свое частное решение (25.3),

причем каждой частоте

соответствуют свои значения А, В и .

Поэтому, определив из (25.5)

, получим две совокупности

частных решений вида (25.3):

(1) (1)

1111 2111

(2) (2)

12222222

sin( ), sin( ),

sin( ), sin( ).

q A kt q B kt

 



(25.6)

Из уравнений (25.4) следует, что для каждой частоты

амплитуды

(

1, 2i 

) связаны друг с другом. Для записи этой связи можно

воспользоваться любым из уравнений (25.4):

1 11 11 1 21 21 1

1 12 12 1 22 22 1

2 11 11 2 21 21 2

2 12 12 2 22 22 2

Bcak cak

Acak cak

Bcak cak

Acak cak



  





  





(25.7)

т. е.

111

BA

, а

222

BA

. Тогда частные решения (25.6) принимают вид:

(1) (1)

1111 21111

(2) (2)

122222222

sin( ), sin( ),

sin( ), sin( ).

q A kt q A kt

 



(25.8)

Колебания, определяемые уравнениями (25.8), называются

главными

колебаниями

, а их частоты



собственными частотами системы.

Колебание с частотой

(всегда меньшей) называют первым главным

колебанием

, а с частотой



вторым главным колебанием.

Числа



, определяющие отношения амплитуд (или обобщенных

координат

/qq

) в каждом из этих колебаний, называются коэффициентами

формы

. Эти коэффициенты показывают во сколько раз амплитуда соответ-

ствующего главного колебания одной из обобщенных координат больше

(или меньше) амплитуды другой обобщенной координаты.

Поскольку частные решения (1.37) являются линейно независимыми,

то общее решение системы дифференциальных уравнений (25.2) будет равно

их линейной комбинацией:

111 1 1 1 2 2 2

222 11 1 1 22 2 2

sin( ) sin( ),

sin( ) sin( ).

qqq A kt A kt

  



  

(25.9)

Теперь найдем постоянные интегрирования А

, А



, и



. Для этого

в общем виде запишем начальные условия движения системы

110110

220220

0, (0) , (0) ,

(0) , (0) .

tqqqq

qqqq





; (25.10)

Вычислим обобщенные скорости, соответствующие обобщенным коор-

динатам (25.9):

111 1 1 22 2 2

2111 1 1 222 2 2

cos( ) cos( ),

cos( ) cos( ).

qkA kt kA kt

 





 





(25.11)

Подставляя начальные условия (25.10) в (25.9) и (25.11), получаем:

10 1 1 2 2

20 1 1 1 2 2 2

10 1 1 1 2 2 2

20 1 1 1 1 2 2 2 2

sin sin ,

cos cos ,

cos cos .

qA A

qkA kA



   

 

  

Решая эти уравнения, найдем амплитуды и начальные фазы

, А

, α

20 2 10

120210

12 1

20 1 10

220110

21 2

1()

() ,

1()

() ,

Aqq













(25.12)

20 2 10

20 1 10

arctg ,

arctg .





































Проведенный анализ показывает, что движения системы с двумя степе-

нями свободы около положения устойчивого равновесия слагаются из

двух независимых колебаний, которые называются собственными формами

колебаний с соответствующей собственной частотой (

или k

Коэффициенты форм



в совокупности описывают

конфигурацию системы при наибольшем ее отклонении от положения

равновесия в процессе свободных колебаний с соответствующей собственной

частотой.

Из (25.8) видно, что координаты

в каждом главном колебании

изменяются по гармоническому закону, имея одинаковые частоты и фазы: