Валькова Т.А. и др. Теоретическая механика

)(m F

z



, и значит, обладают такими же свойствами. Например, из (8.9)

получаем простое правило вычисления

)(m Vm

Z



:

1

m( ) m ( )

zO

mV mV mV h





rr

, (16.4)

т. е. момент количества движения точки относительно оси Оz равен

алгебраическому моменту проекции



Vm



вектора количества движения на

перпендикулярную оси Оz плоскость I относительно точки О пересечения

данной оси с этой плоскостью (рис. 16.1).

В (16.4) h

1

 плечо вектора



Vm



относительно точки О. Причем

)(m Vm

Z



> 0, если с положительного конца оси поворот при действии вектора



Vm



виден происходящим вокруг точки О против хода часовой стрелки,

и

)(m Vm

Z



< 0, если поворот  по ходу часовой стрелки.

В декартовой системе координат

kVmjVmiVmVm

zyхO



 )(m)(m)(m)(m

, (16.5)

где

)(m ),(m ),(m VmVmVm

zyх



 моменты количества движения точки

относительно осей х, у, z

соответственно.

Тогда модуль момента количества движения точки относительно

центра О равен

222

m( ) m( ) m( ) m( )

O х yz

mV mV mV mV







rrrr

r

. (16.6)

Рассмотрим механическую систему, состоящую из n материальных

точек.

Главным моментом количеств движения (кинетическим моментом)

системы относительно центра О называется вектор

O

K



, равный

геометрической сумме моментов количеств движения всех точек системы

относительно этого центра:







n

i

n

i

iiiiiOO

VmrVmK

11

)(m



. (16.7)

Здесь

i

r



 радиус вектор i-й точки системы, проведенный из центра О,

ii

Vm





вектор ее количества движения.

В декартовой системе координат кинетический момент системы

O

K



может быть разложен по трем ортогональным осям

Ox y z

K

Ki K j Kk

r

rr

,

где его проекции

x

K

,

y

K

,

z

K

определяются как моменты количества

движения точек системы относительно соответствующих координатных

осей:

111

m ( ), m ( ), m ( ).

nnn

x x ii y y ii z z ii

iii

KmVKmVKmV





rrr

(16.8)

Ниже будет показано, что главный момент количества движения

(кинетический момент) системы является характеристикой ее

вращательного движения.

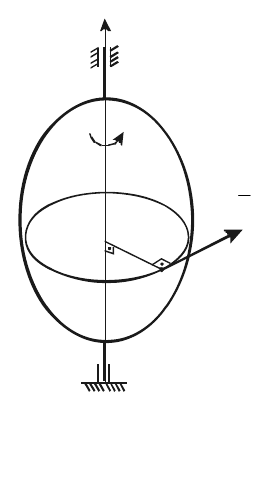
Вычислим кинетический момент твердого тела относительно оси

вращения Оz, если угловая скорость тела в данный момент времени равна

ω

(рис. 16.2). Любая i-я точка тела при его движении будет описывать

окружность радиусом

zi

h

в перпендикулярной оси Оz плоскости. Вектор ее

количества движения

ii

Vm



будет лежать в этой

плоскости перпендикулярно радиусу

zi

h

, причем его

модуль

ω

ii izi

mV mh

.

Тогда из (16.8) имеем

2

111

m( ) ω.

nnn

z z ii iizi izi

iii

KmVmVhmh



















r

Так как согласно (14.12)

2

1

,

n

izi z

i

mh I













то

окончательно получаем

ω .

zz

KI



(16.9)

Следовательно, кинетический момент

вращающегося тела относительно оси вращения равен произведению

момента инерции тела относительно этой оси на угловую скорость тела.

Если система состоит из n тел, вращающихся вокруг оси Оz

с угловыми

скоростями

12

ω , ω ,...,ω

n

соответственно, то

11 2 2

ω ω ... ω .

zz z nzn

K

I I I





ё (16.10)

Теорема об изменении кинетического момента

механической системы

Вычислим производную по времени от кинетического момента

системы относительно неподвижного центра О:

O

z



i

h

z

V

m

ii

Рис.16.2



11

nn

O

iii iii

ii

dK d d

rmV rmV

dt dt dt













r

rr

11 11

()

.

nn nn

iii

ii i i ii i ii

ii ii

dr d mV

mV r V mV r mr

dt dt

 

 

 

r

rrr

&&

(16.11)

Здесь

1

0

n

iii

i

VmV







rr

, так как

sin sin 0 0

o

iii

VmV











rr

.

С учетом (15.1) вторая сумма в (16.11) принимает вид





11 1 1

11

m ( ) m ( ) .

nn n n

ei e i

i ii i i i ii ii

ii i i

nn

ei

Oi Oi

ii

rmr r F F rF rF

FF

  



 



  



rr r r

rr r r r

&&

rr

(16.12)

По второму свойству внутренних сил (14.4) сумма моментов всех

внутренних сил системы относительно произвольного центра О равна нулю,

поэтому

1

m ( ) 0

n

i

Oi

i

F





r

. (16.13)

Тогда с учетом (16.12) и (16.13) выражение (16.11) принимает вид

1

m( ) M ,

n

ee

O

Oi O

i

dK

F

dt







r

rr

r

(16.14)

где

M

e

O

r

 главный момент внешних сил относительно центра О.

Уравнение (16.14) выражает

теорему об изменении кинетического

момента механической системы

: производная по времени от

кинетического момента механической системы относительно какого-либо

центра равна геометрической сумме моментов внешних сил, действующих

на систему, относительно того же центра.

Проецируя (16.14) на неподвижные декартовые оси Охуz, получим

теорему моментов относительно этих осей:

1

m( ) M;

m( ) M.

n

ee

x

ix

i

n

y

ee

yi y

i

n

ee

z

zi z

i

dK

F

dt

dK

F

dt

dK

F

dt







r

(16.15)

Теоремами (16.14) и (16.15) удобно пользоваться при изучении

вращательного движения твердого тела вокруг неподвижной оси или точки.

Следствия:

1. Если геометрическая сумма моментов внешних сил системы

относительно данного центра равна нулю, то кинетический момент

системы относительно того же центра постоянен по модулю и

направлению.

Действительно, если

1

m( ) M 0,

n

ee

Oi O

i

F





rr

r

то

/0

O

dK dt 

r

и

const

O

K 

uuuuur

r

. (16.16)

Этот результат имеет место в случае движения материальной точки под

действием центральной силы, линия действия которой все время проходит

через данный центр О (например, движение Земли под действием

гравитационной силы притяжения к Солнцу).

2. Кинетический момент системы относительно какой-либо

координатной оси постоянен, если сумма моментов внешних сил системы

относительно

этой оси равна нулю.

Если

1

m( ) M 0

n

ee

zi z

i

F







r

, то

/0

z

dK dt



, а, следовательно,

const

z

K



. (16.17)

В частности это имеет место, когда внешние силы системы параллельны оси

или ее пересекают.

Следствия (16.16) и (16.17) выражают законы сохранения

кинетического момента для механической системы и представляют собой

первые интегралы уравнений движения. Согласно (16.14) и (16.15)

внутренние силы непосредственно не могут изменить кинетический момент

системы.

Отметим (без доказательства), что для осей, движущихся

поступательно

с центром масс С системы, теорема моментов относительно

центра масс сохраняет тот же вид, что и относительно неподвижного центра

О, т. е.

. )F(m

dt

Kd

n

i

e

iС

С





1



(16.18)

Для одной материальной точки с учетом (10.4) теорема (16.14)

принимает вид:

m( )

O

dmV

R

dt



r

. (16.19)

Производная по времени от момента количества движения

материальной точки относительно какого-либо центра равна момент

равнодействующей сил, приложенных к точке, относительно того же

центра.

В декартовой системе координат векторное уравнение (16.19)

эквивалентно трем скалярным равенствам. Принимая центр О за начало

декартовой системы координат Охуz, получим

()()

dd

rmV rR

dt dt





rr

ss

или в виде определителей третьего порядка

.

xyz

i

j

ki

j

k

d

xy

zx

y

z

dt

mx m

y

mz R R R



rr

rr rr

&&

&

Отсюда

() ,

() .

zy

x

z

yx

d

myzzyyFzF

dt

d

mzxxzzFxF

dt

d

mxyyxxFyF

dt



 















&

&&

(16.20)

Отметим, что интегрирование (16.20) возможно, когда известны зависимости

координат материальной точки х, у, z от времени, но тогда вообще отпадает

надобность в применении равенств (16.20). Однако существует случай

движения точки под действием центральной силы, когда имеет место

интеграл движения (16.16), и момент количества движения точки

относительно центра О является постоянной величиной:

m ( ) const

O

mV r mV 

uuuuur

rr

r

.

Тогда находим сразу три первых интегралов движения для

материальной точки:

12 3

( ) , ( ) , ( ) .myz zy C mzx xz C mxy yx C



 

&& &&

&&

ЛЕКЦИЯ 17

ТЕОРЕМЫ ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ

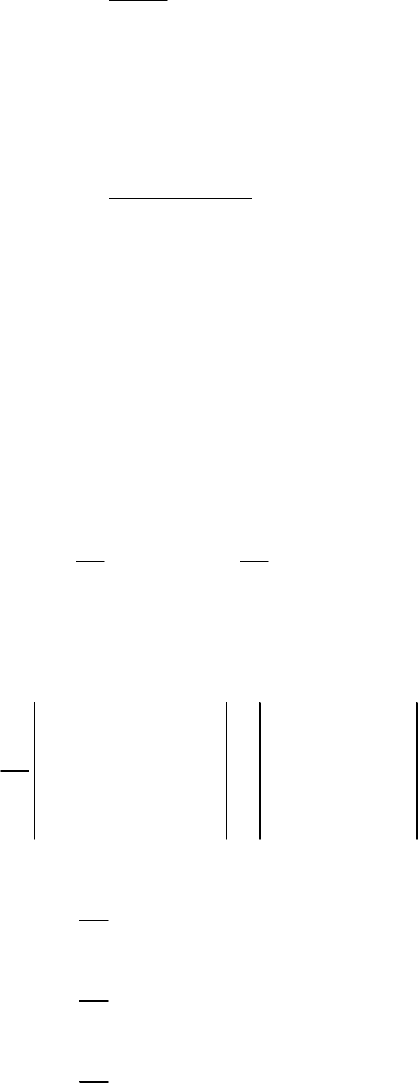
Работа силы. Мощность

Рассмотрим материальную точку В, движущуюся относительно

инерциальной системы отсчета Oхуz

, под действием силы

F



(рис. 17.1).

Элементарной работой силы

F



называется скалярное произведение

силы на вектор элементарного перемещения

r

d



точки ее приложения:

dA F dr





r

, (17.1)

или

cosαdA F ds



. (17.2)

Здесь

F

 модуль силы,

ds dr

r

 модуль элементарного перемещения,

α



угол между векторами

F



и

r

d



.

Разложим силу

F



на касательную



F



и нормальную

n

F



составляющие.

Поскольку

τ

cosαFF

, то (17.2) принимает вид

τ

dA F ds



. (17.3)

Согласно (17.3) элементарную

работу совершает касательная

составляющая силы

ττ

dV

Fmam

dt



.

Определение (17.3)

соответствует представлению о

работе как мере такого действия

силы

F



, которое приводит к

изменению модуля скорости точки,

а, следовательно, ее кинетической

энергии (см. ниже).

Знак элементарной работы

F

τ

F

n

r

d

r

z

α

x

y

k

j

O

i

B

0

B

1

V

F

Рис. 17.1

определяется знаком

cosα

:

1) если

τ

π

0 α ,0, 0

2

F dA  

 сила ускоряет движение точки;

2) если

τ

π

απ,0, 0

2

F dA  

 сила замедляет движение точки;

3) если

τ

π

α , 0, 0

2

F dA

 точка движется равномерно.

Следовательно, если сила перпендикулярна элементарному

перемещению, то ее элементарная работа равна нулю.

В декартовой системе координат поскольку

,

xyz

FFiFjFk

dr dxi dyj dzk



r

rr

r

rr

r

,

и выражение (17.1) принимает вид

xyz

dA F dx F dy F dz





, (17.4)

где

, , ,

xyz

F F F

, , dx dy dz

 проекции векторов

F



и

r

d



на оси х, у, z.

Пусть материальная точка В совершает конечное перемещение из

положение В

о

в положение В

1

, описывая дугу

01

B

B

(рис. 17.1). Работа силы

F



на конечном перемещении

01

B

B

равна криволинейному интегралу,

взятому от элементарной работы вдоль этого перемещения:

11 1

01

00 0

BB B

BB

BB B

А

dA F dr F ds









r

, (17.5)

или в декартовых координатах



1

01

0

B

BB x y z

B

А

Fdx Fd

y

Fdz



. (17.6)

В системе СИ единицей измерения работы является 1 джоуль (1Дж = 1 Н м).

Мощностью N называется величина, определяющая работу,

совершаемую силой в единицу времени:

τ

dA F ds

NFV

dt dt

 

. (17.7)

Мощность равна произведению касательной составляющей силы на скорость.

Если работа совершается равномерно, то мощность

1

A

N

t



, (17.8)

где t

1

 время в течение которого, совершена работа А.

Единицей измерения мощности в СИ является ватт (1 Вт = 1 Дж/c).

В технике за единицу мощности иногда принимается лошадиная сила

(1 л.с. = 736 Дж).

Из (12.8) следует, что

1

A

Nt



, и работу, произведенную машиной,

измеряют в киловатт-часах (1кВ ч = 3,6 10

6

Дж).

В ряде случаев для вычисления работы сил удобно использовать

готовые формулы. Получим некоторые из них.

1.

Работа постоянной силы

constF 

uuuuur

r

на прямолинейном

перемещении

(рис. 17.2) определяется по

формуле (17.5):

1

01

0

τ 1

cosα

B

BB

B

А

FdsF s



, (17.9)

где s

1

 расстояние между точками В

о

и В

1

.

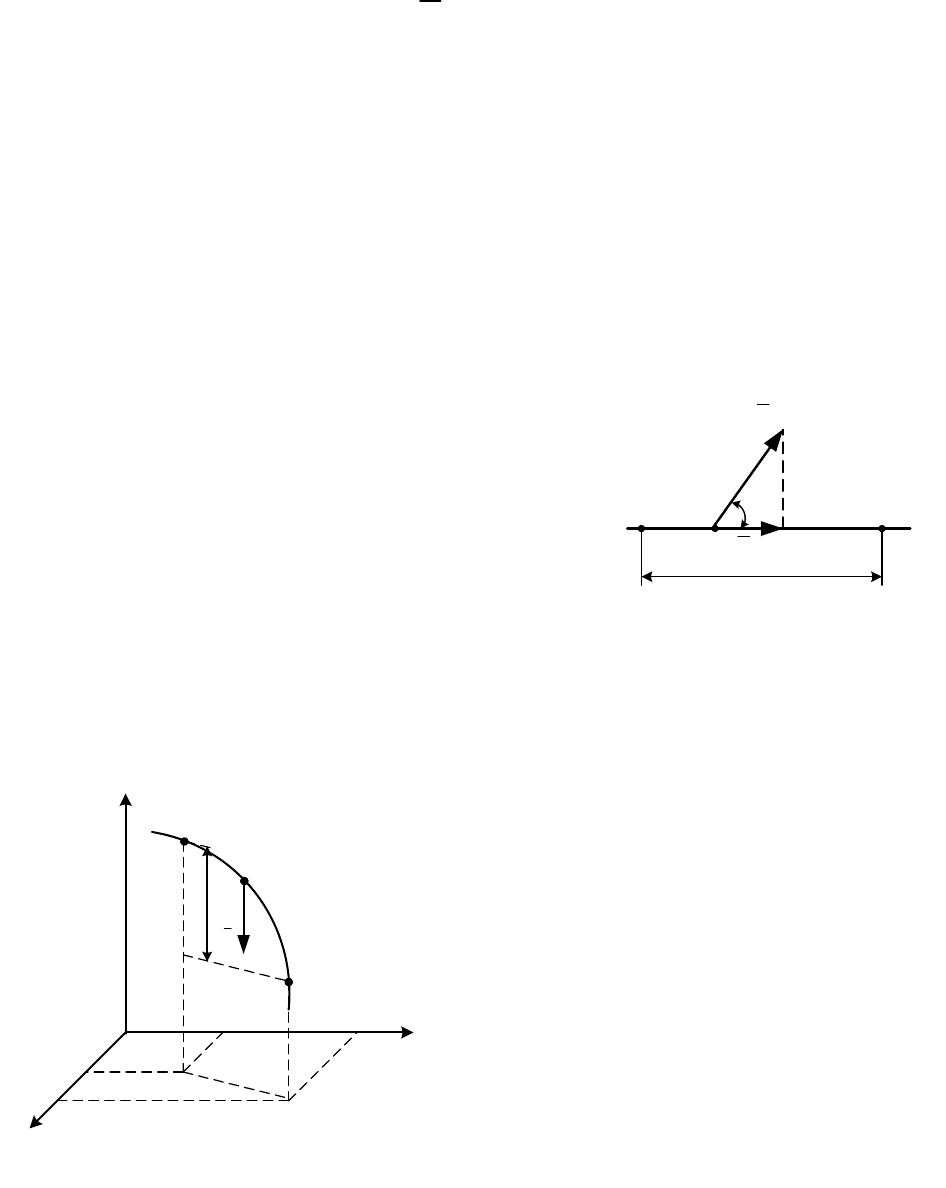
2.

Работа силы тяжести. Пусть точка В,

на которую действует сила тяжести

P



(рис. 17.3), перемещается из

положения В

о

(х

о

, у

о

, z

о

) в положение В

1

(х

1

, у

1

, z

1

).

В выбранной системе координат

0, 0,

xyz

P

PPP





. Подставляя

эти значения в (17.6), вычислим работу

силы

P



на перемещении

01

B

B

:

  

1

0

01

z

А

(P) P dz P z z  



r

.

Если точка В

0

выше В

1

, то

01

zzh





,

где h  вертикальное перемещение

точки В; если точка В

0

ниже В

1

, то





h zzzz 







o11o

.

Следовательно,

F

τ

α

B

1

B

0

s

1

Рис. 17.2

z

B

1

B

0

x

y

O

P

y

1

y

0

z

1

z

h

1

x

0

x

Рис. 17.3





01

() ,

А

PPzz Ph

r

(17.10)

т. е. работа силы тяжести равна взятому со знаком плюс или минус произ-

ведению модуля силы на вертикальное перемещение точки ее приложения.

Работа положительна, если точка

В приложения силы

P



опускается, и

отрицательна, если точка

В поднимается над земной поверхностью.

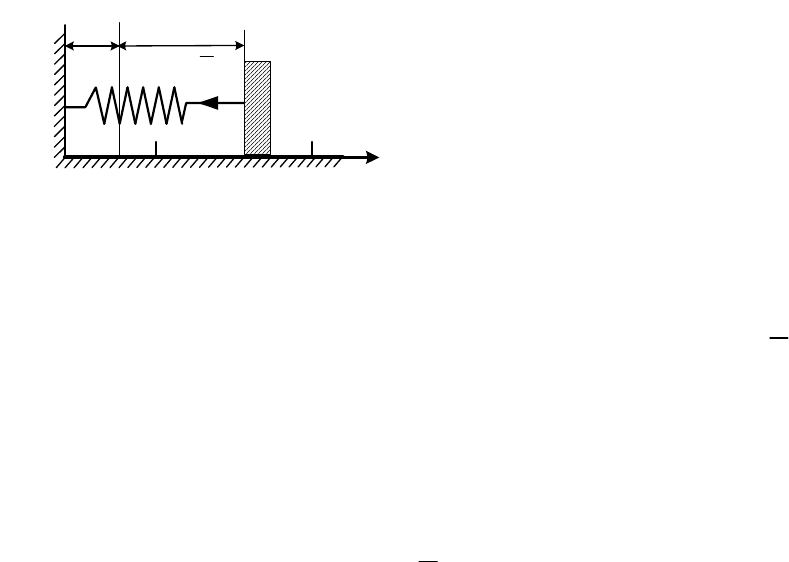
3.

Работа силы упругости. Рассмотрим груз В, движущийся по

гладкой горизонтальной плоскости из положения В

0

(х

0

) в положение В

1

(х

1

)

(рис. 17.4). К грузу прикреплена пружина жесткости c, длина недеформиро-

ванной пружины  l

0

. Поместим начало отсчета оси Ох в конец недефор-

мированной пружины. Тогда в произвольном положении груза В

деформация

пружины

λ

х



и на груз действует сила упругости:

λ

упр

Fccx



,

проекции, которой на декартовые оси

,0.

x упр yz

FF c x FF



 

Вычислим работу, совершаемую силой

упругости, на перемещении

01

B

,

используя формулу (11.6):



1

0

22

01

()

2

x

упр

x

c

А

Fcxdx xx  



r

Здесь

00

λx 

 начальная деформация (удлинение) пружины, а

11

λx





деформация пружины в конечном положении В

1

. Следовательно,



22

0 1

() λλ,

2

упр

c

А F 

r

(12.11)

работа силы упругости равна половине произведения коэффициента

жесткости на разность квадратов начальной и конечной деформаций

(удлинений или сжатий) пружины.

Работа будет положительной, если

01

λλ

, т. е. когда деформация

пружины после совершения работы уменьшается, и работа будет

отрицательная, если

01

λλ

, т. е. когда за счет работы деформация пружины

увеличивается.

4.

Работа реакции шероховатой поверхности. Рассмотрим точку В,

движущуюся по шероховатой поверхности или кривой из положения В

0

в В

1

(рис. 17.5) . Разложим реакцию шероховатой поверхности на составляющие:

С

O

F

упр

B

x

B

1

(

x

)

B

0

(

x

)

0

λ

0

l

Рис. 17.4

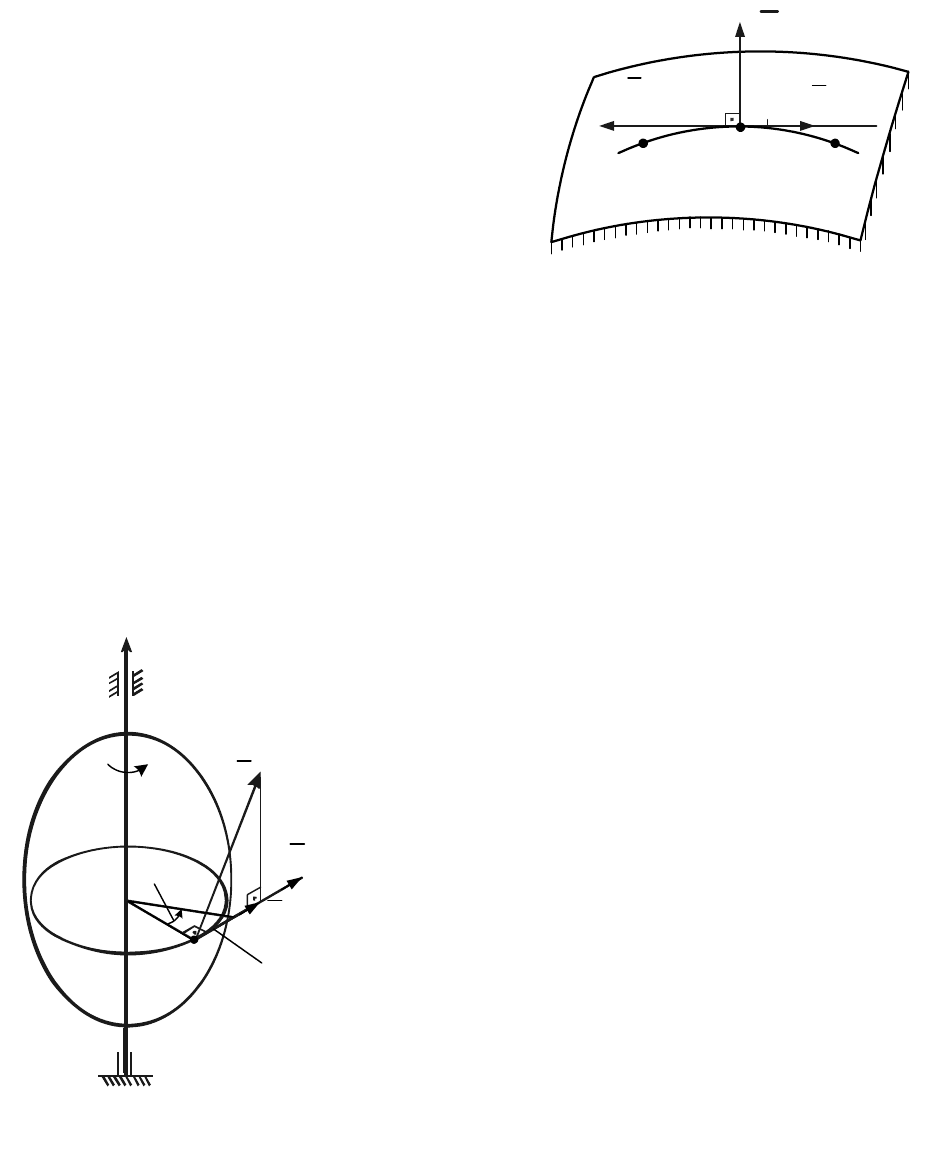
N



 нормальную реакцию поверхности и силу трения

тр

F



, модуль которой

NfF

тр



, где f  коэффициент трения.

Работа нормальной реакции

N



всегда равна нулю, так как из (17.2)

() cos90 0

o

dA N N ds



. (17.12)

Работа силы трения

тр

F



при движении материальной точки по

шероховатой поверхности (рис. 17.5) из положения В

0

в положение В

1

определяется по формуле (17.5):



11

00

.

BB

тр тр

BB

А

F F ds f N ds 



r

Если величина силы трения постоянная

const

тр

FfN

, то ее работа равна



1

0

1

B

тр

B

А

Ff N dsfNs  



r

, (17.13)

где s

1

 длина дуги кривой В

0

В

1

, по

которой перемещается точка В. Следовательно, работа силы трения всегда

отрицательна.

5.

Работа силы, приложенной к вращающемуся телу. Элементарная

работа силы

F



, приложенной к вращающемуся телу (рис. 17.6), согласно

(17.3) равна

ττ

dA F ds F h d





,

так как

ds h d





, где

d



 элементарный угол

поворота тела.

Поскольку

τ

m( ) M

zz

Fh F

r



вращающий момент, тогда в общем случае

получим

M.

z

dA d







(17.14)

Элементарная работа (17.14) положительна,

если

M

z

 вращающий момент, т. е.

M

z

и

d



направлены в одну сторону. Работа (17.14)

отрицательна, если

M

z

 момент сопротивления

ds

B

1

B

0

N

F

тр

V

τ

Рис. 17.5



ds

O

F

B

z

V



F

h

C



d

Рис. 17.6

Валькова Т.А. и др. Теоретическая механика

Подождите немного. Документ загружается.