Валькова Т.А. и др. Теоретическая механика

Подождите немного. Документ загружается.

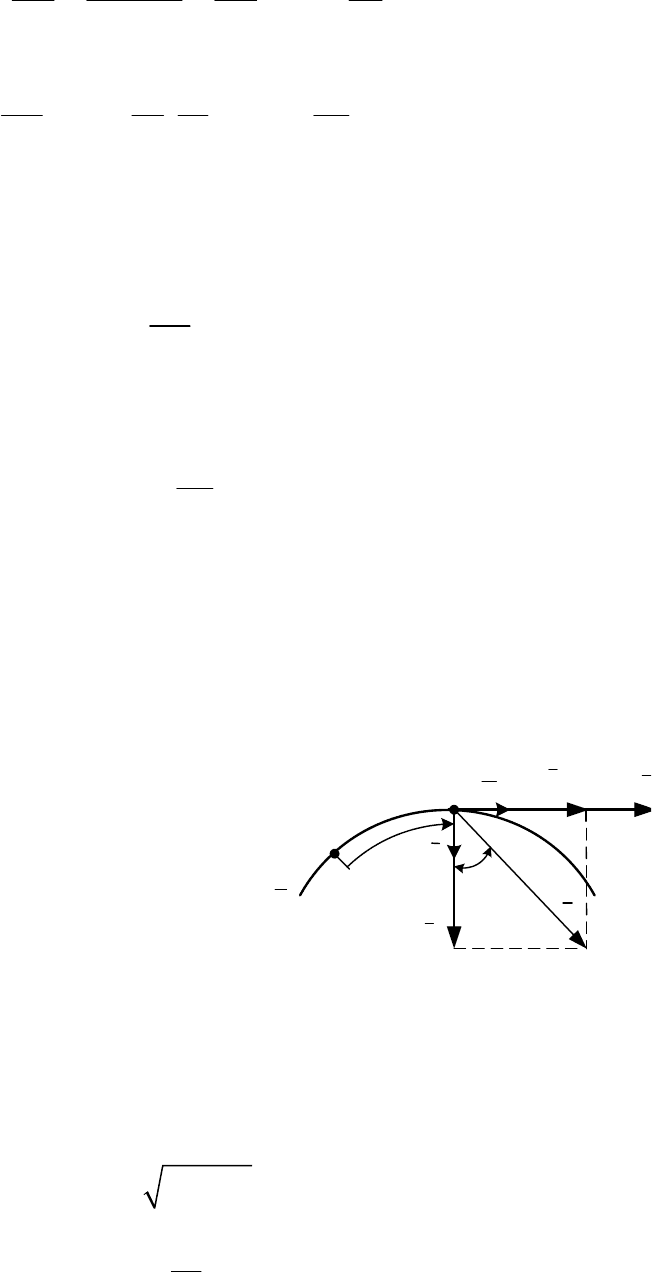
( τ ) τ

dV d V dV d

a V

dt dt dt dt

   

ττ

dV d ds

V s n

dt ds dt

 

или

τ n

aa a





rr r

. (1.13)

Здесь

τ τ



rrr

(1.14)

вектор касательного ускорения точки, его числовое значение

as 

, а

a n

(1.15)

вектор нормального ускорения точки, его числовое значение

/ ρ / ρ

aV s

Формула (1.13) выражает

теорему Гюйгенса: ускорение точки при

криволинейном движении равно геометрической сумме касательного и

нормального ускорений. Из (1.13) следует, что проекция ускорения точки на

бинормаль всегда равна нулю:



Вектор касательного ускорения





направлен в точке М по касательной к

траектории в соответствии со знаком

(аналогично вектору скорости



Вектор нормального ускорения



направлен вдоль главной нормали к

центру кривизны траектории (рис. 1.4).

Поскольку векторы





взаимно

перпендикулярны, то вектор ускорения



точки М изобразим диагональю

прямоугольника, построенного на составляющих





как на сторонах.

Его модуль и направление определяются по формулам

τ n

aaa





; (1.16)

tg β



. (1.17)



(+)( )

Рис. 1.4

Если знаки



Vs

в данный момент времени одинаковые (оба

положительные (рис. 1.4) или отрицательные), то точка движется ускоренно,

а если знаки противоположные  замедленно.

Рассмотрим некоторые частные случаи движения точки.

Прямолинейное движение точки. Так как траекторией точки является

прямая линия, то

ρ 

. Тогда

/ ρ 0



/a a dV dt



. Касательное

ускорение характеризует изменение скорости по величине.

Равномерное криволинейное движение точки. При этом движении

величина скорости точки остается постоянной

constV 

, поэтому

/0adVdt

, и

/ρ

aa V n

rr r

, т. е. вектор ускорения точки



направлен

по главной нормали. Нормальное ускорение точки характеризует изменение

ее скорости по направлению.

Определим закон равномерного криволинейного движения точки, если

при

0,t ss

. Так как



, то

ds V dt



, тогда

ds V dt



sVt





. (1.18)

Формула (1.18) определяет закон равномерного движения точки.

Равнопеременное криволинейное движение точки. При этом

движении

consta 

. Определим скорость точки и закон ее движения по

известной кривой. Пусть при

t = 0, s = s

, V = V

. Поскольку

/adVdt

, то

dV a dt

;

dV a dt



Следовательно,

0 τ

VV at





или

taVV





, (1.19)

где знак «+» соответствует равноускоренному движению, а знак «

» 

равнозамедленному движению точки.

С учетом (1.12), выражение (1.19) запишем в виде

0 τ

Vat



Отсюда

0 τ

st t

ds V dt a t dt





a t

ss V t  

. (1.20)

Формула (1.20) определяет закон равнопеременного криволинейного

движения точки

Равномерное прямолинейное движение точки. В этом случае вектор

скорости не изменяется ни по величине, ни по направлению:



0a 

. Таким образом, единственным движением, при котором ускорение

точки равно нулю, является равномерное прямолинейное движение

Определим касательное и нормальное ускорения точки и значение

радиуса кривизны ее траектории, если движение точки задано в

координатной форме (1.3):

( ); ( ); ( )

xt y yt z zt

Из (1.8) имеем

2222

VVVV

. Вычислим производную по времени от

данного равенства:

2222

xyyzz

VVV VV VV



отсюда

()/

xx yy zz

aVaVaVaV

  

. (1.21)

Из (1.16) находим нормальное ускорение точки

aaa







. (1.22)

Тогда значение радиуса кривизны траектории в точке М определим

по формуле

ρ .



(1.23)

ЛЕКЦИЯ 2

КИНЕМАТИКА ТВЕРДОГО ТЕЛА

Поступательное движение твердого тела

Поступательным называется движение твердого тела, при котором

любая прямая, проведенная в теле, перемещается, оставаясь параллельной

своему первоначальному положению.

При поступательном движении точки тела

могут двигаться по любым траекториям.

Например, кузов автомобиля на прямолинейном

горизонтальном участке дороги движется

поступательно: траекториями его точек будут

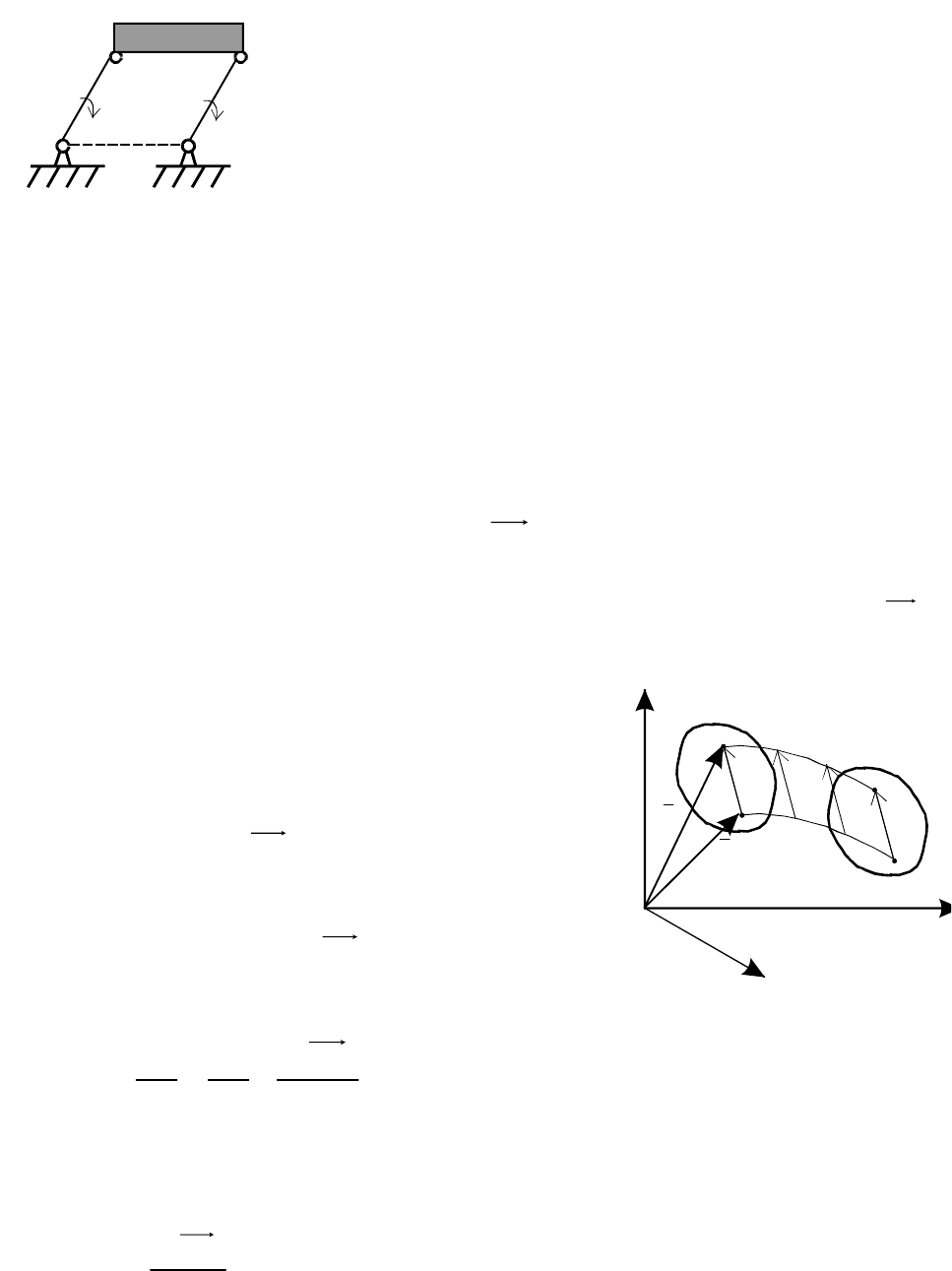
прямые линии. Спарник

АВ (рис. 2.1) при

вращении кривошипов

А и О

В (О

А = О

В =

) движется поступательно: траекториями точек

спарника являются окружности радиусом

Теорема. При поступательном движении твердого тела все его точки

описывают одинаковые траектории и в каждый момент времени имеют

геометрически равные скорости и ускорения.

Доказательство. Рассмотрим твердое тело, совершающее

поступательное движение относительно неподвижной системы координат

Охуz. Возьмем две произвольные точки А и В, положения которых в момент

времени

t связаны равенством (рис. 2.2):

ABrr





, (2.1)

где



 радиус-векторы точек А и В соответственно. Вектор

является постоянным по модулю и направлению, так как тело абсолютно

твердое и оно движется

поступательно.

Из (2.1) следует, что для любого

момента времени положение точки

можно получить, смещением точки

А на

постоянный вектор

. Следовательно,

траектория точки

В тождественна

траектории точки

А, но смещена

относительно ее на вектор

Дифференцируя равенство (2.1) по

времени, получим

)ABd(





или





, (2.2)

поскольку

0

)ABd(

Рис. 2.1

Таким образом, скорости точек А и В в любой момент времени

геометрически равны.

При дифференцировании равенства (2.2) по

времени имеем





или





, (2.3)

т. е. ускорения точек А и В тела также

геометрически равны.

Поскольку изначально точки

А и В выбраны

произвольно, то это означает, что траектории всех

точек тела при поступательном движении будут

одинаковы, а их скорости и ускорения в любой

момент времени геометрически равны.

Следовательно,

изучение поступательного движения твердого тела

сводится к задаче кинематики любой одной его точки

(см. лекцию 1).

ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА

ВОКРУГ НЕПОДВИЖНОЙ ОСИ

Угловая скорость и угловое ускорение

Вращательным движением твердого тела вокруг неподвижной оси

называется движение твердого тела, имеющего две неподвижные точки (А и В).

Прямая

OZ, проходящая через эти точки, называется осью вращения.

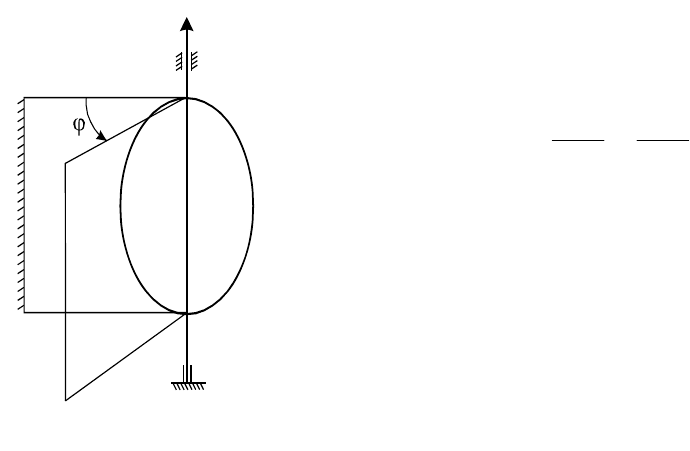
Для определения положения вращающегося тела возьмем две

полуплоскости I и II, ограниченные осью вращения

OZ (рис. 2.3).

Полуплоскость I неподвижная, а полуплоскость II врезана в тело и

вращается вместе с ним. Тогда положение тела в произвольный момент

времени

t определяют заданием линейного угла



двухгранного угла между

этими полуплоскостями:

)(





. (2.4)

Угол



называется углом поворота тела. Уравнение (2.4) определяет

закон вращательного движения твердого тела вокруг неподвижной оси.

За положительное направление отсчета угла



выбрано направление

против хода часовой стрелки. В системе СИ угол



измеряется в радианах.

Основными кинематическими характеристиками вращательного

движения твердого тела являются

угловая скорость и угловое ускорение.

Рис. 2.3

Пусть за промежуток времени

ttt





тело повернется вокруг оси OZ

на угол



. Угловой скоростью тела в данный момент времени t

называется скалярная величина

ω lim

tdt















. (2.5)

Числовое значение угловой скорости равно первой производной от угла

поворота тела по времени

Угловая скорость характеризует изменение угла поворота тела в

единицу времени. Угловая скорость измеряется в рад/с или



. Знак в (2.5)

определяет направление вращения тела.

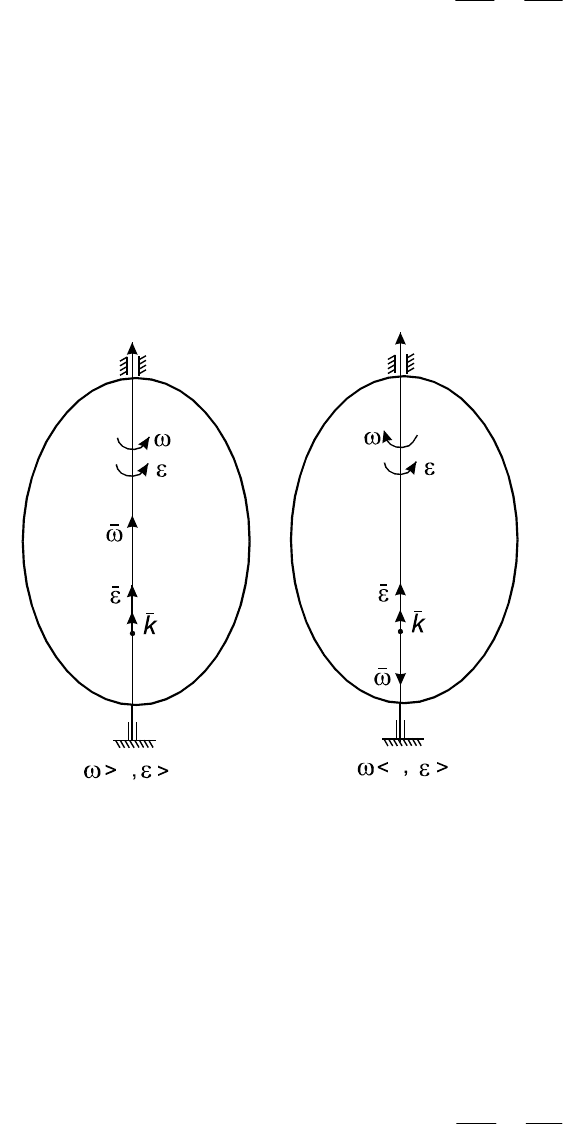
Если

ω 0

, то вращение

вокруг оси

OZ происходит

против хода часовой стрелки

(рис. 2.4,

а), а если

ω 0



тогда по ходу часовой стрелки

(рис. 2.4,

б).

Угловую скорость

можно изобразить в виде

вектора, направленного по оси

вращения:

ω kk





, (2.6)

где



 орт оси OZ. Вектор

направлен вдоль оси

OZ, если

ω 0





, и против оси OZ,

если

ω 0





, т. е. с конца

вектора

вращение вокруг

оси всегда видно происходящим против хода часовой стрелки (рис. 2.4).

Если за время Δ

t = t

 t угловая скорость изменилась на величину

Δω = ω

 ω, то угловым ускорением тела в данный момент времени t

называется величина ε, определяемая выражением

ωω

ε lim

tdt









или





. (2.7)

а б

Рис. 2.4

Числовое значение углового ускорения тела равно первой производной от

угловой скорости или второй производной от угла поворота тела по

времени.

Угловое ускорение ε характеризует изменение угловой скорости ω тела

в единицу времени. В качестве единицы измерения

обычно используется

рад/c

или с

2

Угловое ускорение тела можно изобразить в виде вектора

направленного по оси вращения OZ:





&&&

. (2.8)

Если величина угловой скорости с течением времени возрастает, то

вращение тела является ускоренным. В этом случае векторы

направлены в одну сторону, а их числовые значения имеют одинаковые

знаки (или

0ε 0,ω 

(рис. 2.4, а), или

0ε 0,ω



Если величина угловой скорости с течением времени уменьшается, то

вращение тела является замедленным. Векторы

направлены по оси

вращения в противоположные стороны, а их числовые значения имеют

противоположные знаки (

0ε 0,ω





, или

0ε 0,ω 



(рис. 2.4, б)).

Равномерное вращение. Если угловая скорость тела остается во время

движения постоянной, то вращение тела называется равномерным. Найдем

закон равномерного вращения. Пусть при t = 0

(0)







ω(0) ω const

Согласно (2.5) запишем

в дифференциальной форме







или

ddt





Возьмем от обеих частей этого равенства определенные интегралы,

у которых нижние пределы соответствуют начальным условиям движения,

а верхние  произвольному моменту времени t:

ddt







Отсюда следует закон равномерного вращения:



 

. (2.9)

Равнопеременное вращение. Если угловое ускорение при движении

тела остается постоянным по величине (ε = const), то вращение называется

равнопеременным. Найдем закон равнопеременного вращения. Пусть при

t = 0, φ(0) = φ

, ω(0) = ω

. Согласно (2.7) запишем ε в дифференциальной

форме



или, разделяя переменные,

ωε ddt



Интегрируя, получим

ω 0

ωε

ddt



ω = ω + ε t

или

ωω ε t

. (2.10)

Формула (2.10) выражает зависимость угловой скорости от времени

при равнопеременном вращении твердого тела. Знак «+» соответствует

равноускоренному, а знак «»  равнозамедленному вращениям.

Воспользовавшись (2.5), представим (2.10) в виде



 

или

ω ε dtdt tdt 

Интегрируя данное уравнение с учетом начальных условий движения

ωε

d tdt t dt



 





получим закон равнопеременного вращения

  

. (2.11)

Знак «+» в (2.11) соответствует равноускоренному, а знак «» 

равнозамедленному вращениям.

Скорости и ускорения точек вращающегося тела

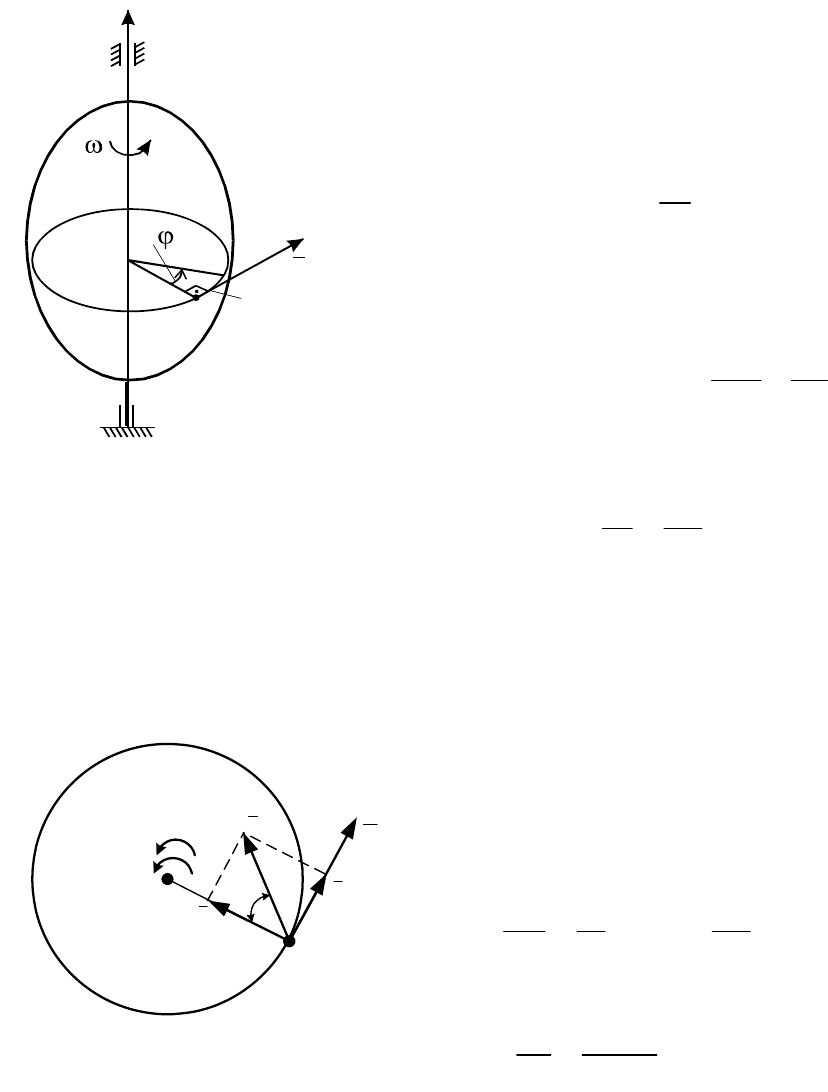
Пусть тело вращается вокруг оси OZ и имеет в данный момент времени

угловую скорость

и угловое ускорение

(ω > 0, ε > 0). Рассмотрим

произвольную точку М тела. При вращении тела вокруг оси траекторией

точки М является окружность радиусом R, лежащая в перпендикулярной к

оси плоскости (рис. 2.5).

Вектор скорости



точки М будет

направлен по касательной к этой окружности

(

RV 



) по вращению тела, а его величина

определяется по формуле (1.12)



Выразим элементарное перемещение

точки

М через элементарный угол поворота



тела.

Запишем пропорцию

2π

Rds





. Отсюда

ds R d





. Тогда

ds d

V R R

dt dt



 

. (2.12)

Для определения ускорения точки М воспользуемся теоремой Гюйгенса

(1.13)

τ n

aa a





rr r

. (2.13)

Найдем выражения для касательного

и нормального ускорений точки через

угловую скорость

и угловое ускорение

тела:



ωε

dV d d

a R R R

dt dt dt

  

; (2.14)





 

. (2.15)

Касательное ускорение

направлено по касательной к траектории

в точке М (по вектору



при ускоренном вращении и против вектора



при

Рис. 2.5







Рис. 2.6

замедленном вращении). Вектор нормального ускорения



всегда

направлен

по радиусу вращения МС = R к оси вращения тела (рис. 2.6).

Величина полного ускорения точки вращающегося тела вычисляется

по формуле

22 2 4

εω

aaaR



 

. (2.16)

Отклонение вектора полного ускорения



от радиуса R описываемого

точкой М окружности определяется углом

tg β



. (2.17)

Поскольку точка М выбрана произвольно, то из (2.16) и (2.17) следует,

что ускорения всех точек вращающегося твердого тела пропорциональны их

расстояниям до оси вращения и в данный момент времени образуют

одинаковые углы

с радиусами описываемых ими окружностей.

Выражение скорости точки, касательного и нормального

ускорений в виде векторных произведений

Проведем из произвольной точки О на оси вращения в точку М радиус-

вектор



(рис. 2.7). Также изобразим в точке О векторы

Рассмотрим вектор

ω r



. Вычислив модуль этого вектора

ωωsin αω rr RV   

заметим, что он равен численному значению

скорости точки М. Направления векторов

ω r





также совпадают (оба вектора направлены

перпендикулярно плоскости треугольника

ОМС, т. е. по касательной к окружности в

направлении вращения тела).Следовательно,

ωVr

. (2.18)

Вектор скорости точки вращающегося

тела равен векторному произведению угловой

скорости тела на радиус-вектор точки.

Формула (2.18) называется

формулой Эйлера.

Согласно (1.2),





, и при













Рис. 2.7