Валькова Т.А. и др. Теоретическая механика
Подождите немного. Документ загружается.

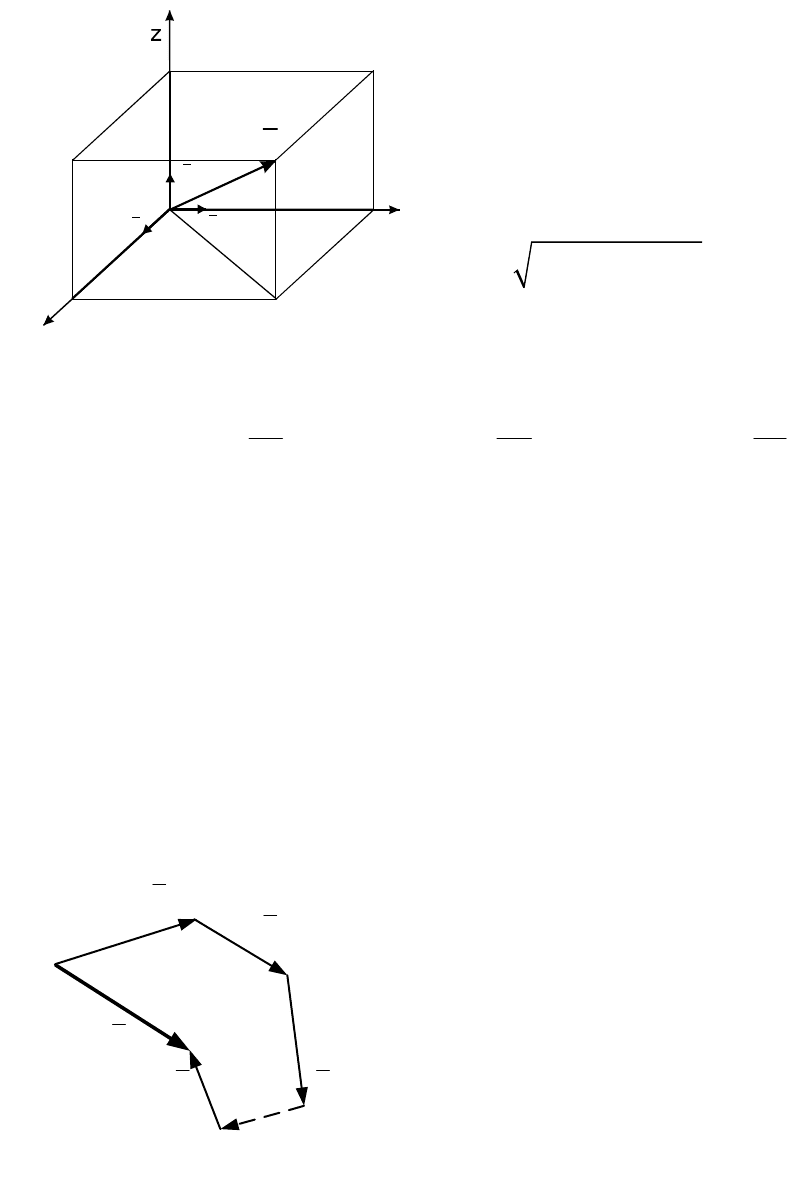
При решении задач механики силу
F
удобно задавать, зная
координаты точки ее приложения и проекции силы
zyх
F,F ,F
на
декартовые оси.
Вектор силы
F
, ее модуль и углы,
которые сила образует с координатными
осями, определяются по формулам
(рис. 5.16):
;
х yz
FFiFjFk
r
r
rr
(5.4)
222
;
xyz
FFFF
(5.5)
. cos , cos , cos
F
F
kF
F
F
jF
F
F
iF
z
y
x
(5.6)
Геометрический способ сложения сил
Пусть на абсолютно твердое тело действует система сходящихся сил
12,3
, , , ...,
n
F
FF F
rrr r
, у которых линии действия пересекаются в точке О.
Найдем их равнодействующую
R
. Для этого перенесем все силы вдоль
линий их действия в точку сходимости
О. Тогда, используя правило
сложения векторов, геометрическая сумма сил
12,3
, , , ...,
n
F
FF F
rrr r
определяется
построением силового многоугольника (рис. 5.17): в точке
О вектор
R
,
соединяющий начало первого вектора
1
F
с
концом последнего вектора
n
F
, изображает
геометрическую сумму слагаемых сил
12,3
, , , ...,
n
FFF F
rrr r
:
12,3
1
..... ;
n
n к
к
RF F F F F
rr r r r r
(5.7)
т. е.
12,3
, , ,....., ~
n
F
FF F R
rrr r r
.
Разложение силы
O
F
1
F
2
F
3
F
n
R
Рис. 5.17
F
x
F
x
O
y
y
F
z
F
i
j
k
Рис. 5.16

Силу можно разложить по выбранным
направлениям на составляющие. Например,
силу
R
на рис. 5.3 можно заменить двумя
силами
1
F
и
2
F
(
21
FFR
), разложив вектор
R
в точке А в направлении действия
составляющих сил
1
F
и
2
F
по правилу
параллелограмма. Силу
F
в пространстве
можно заменить тремя силами
1
F
,
2
F
,
3
F
:
(
123
FFFF
rrrr
) и разложить ее по трем
направлениям. Для этого представляем
F
диагональю параллелепипеда, сторонами которого являются составляющие
1
F
,
2
F
,
3
F
. Обычно для простоты аналитических формул выбирают в точке А три
ортогональных направления. Тогда сила
F
направлена по пространственной
диагонали прямоугольного параллеле-пипеда (рис. 5.18), построенного на
силах
1
F
,
2
F
,
3
F
как на сторонах.
Аналитический способ сложения сил
Воспользуемся
теоремой: проекция вектора суммы на какую-нибудь
ось равна алгебраической сумме проекций слагаемых векторов на ту же ось
.
Проецируя равенство
1
n
к
к
FR
на оси декартовой системы координат
Охуz, получим
111
, , ,
nnn
х
кxy кyz кz
ккк
R
FR FR F
(5.8)
где
, ,
кx кy кz
F
FF
проекции силы
к
F
на оси Ох, Оу, Оz соответственно. Тогда
согласно (5.4)(5.6) вектор
R
, его модуль и направление определяются по
формулам:
;
х yz
R
Ri R j Rk
r
r
rr
(5.9)
222
;
xyz
RRRR
(5.10)
. cos , cos , cos
R
R
kR
R
R
jR
R
R
iR
z
y
x
(5.11)
Равновесие системы сходящихся сил
A
F
1
F
2
F
3
F
Рис. 5.18
Если абсолютно твердое тело находится в равновесии под действием
системы сходящихся сил
12,3
, , , ...,
n
FFF F
rrr r
, то их равнодействующая
1
= 0
n
к
к
RF
rr
. (5.12)
Тогда получаем
0 .....
3,21
n
FFFF
. (5.13)
Следовательно, силовой многоугольник, построенный на силах
12,3
, , , ...,
n
FFF F
rrr r
, является замкнутым, т. е. конец силы
n
F
совпадает с
началом силы
1
F
.
Условие (5.13) называется
геометрическим условием равновесия для
системы сходящихся сил
: необходимым и достаточным условием
равновесия твердого тела под действием системы сходящихся сил является
замкнутость силового многоугольника, построенного на этих силах.
Аналитически условие (5.12) с учетом (5.9) означает, что
0, 0, 0
х yz
RRR
или согласно (5.8)
11 1
0 , 0 , 0 .
nn n
кx кy кz
кк к
FF F
(5.14)
Уравнения (5.14) называются
аналитическими условиями
равновесия
системы сходящихся сил: для равновесия абсолютно твердого
тела, находящегося под действием системы сходящихся сил, необходимо и
достаточно, чтобы суммы проекций этих сил на каждую из трех
координатных осей были равны нулю.
Если на тело действует плоская система сходящихся сил, то в (5.14)
остается только два уравнения равновесия. Например, для системы сил,
лежащих в
плоскости Оху, аналитические условия равновесия принимают
вид
11
0 , 0 .
nn
кx кy
кк
FF
(5.15)
Теорема о трех силах

Если на абсолютно твердое тело, находящееся в равновесии,
действуют три силы, лежащие в одной плоскости, то линии их действия
пересекаются в одной точке.
Доказательство. Пусть на абсолютно твердое тело действует три силы
1
F
,
2
F
,
3
F
, лежащие в одной плоскости, (рис. 5.19). Перенесем силы
1
F
и
2
F
в
точку С пересечения линий их действия и сложим. Тогда тело будет
находиться в равновесии под действием двух сил: равнодействующей
2121
FFR
и силы
3
F
.
Но согласно аксиоме 1
статики силы
21
R
и
3
F
должны
быть направлены вдоль одной
прямой в противоположные
стороны, и поэтому линия
действия силы
3
F
пересечет
точку С.
Следовательно, линии
действия всех сил
1
F
,
2
F
,
3
F
пересекаются в одной точке С, т. е. плоская система трех сил всегда является
системой сходящихся сил. Теорема доказана.
ЛЕКЦИЯ 6
МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА
Моментом силы
F
r
относительно центра О называется вектор
m( )
O
F
r
r
, равный векторному произведению радиус-вектора
r
r
, проведенного
из центра О в точку А приложения силы, на вектор силы
F
r
:
m( ) .
O
F
rF
rr
r
r
(6.1)
Вектор
m( )
O
F
r
r
приложен в точке О и направлен перпендикулярно плоскости,
проходящей через центр О и силу
F
r
, в ту сторону, откуда сила видна
стремящейся повернуть тело вокруг центра О против хода часовой стрелки
(рис. 6.1).
С
А
1
F
F
2
F
3
1- 2
R
Рис. 5.19

Модуль вектора
m( )
O
F
r
r
равен
произведению модуля
F силы на
плечо h:
m( )
O
FF h
r
. (6.2)
Здесь плечо h перпендикуляр,
опущенный из центра О на линию
действия силы
F
r
.
Момент
m( )
O
F
r
r
характеризует вращательный
эффект силы
F
r
относительно
центра (точки) О.
Свойства:
1. Момент силы относительно центра не изменяется при переносе силы
вдоль линии ее действия в любую точку.
2. Если линия действия силы пересекает центр О (h = 0), то момент
силы относительно центра О равен нулю.
Для плоской системы сил при вычислении моментов сил относительно
точки (центра), лежащей в той же плоскости, пользуются
понятием
алгебраического момента силы относительно точки.
Алгебраический момент силы
F
r
относительно точки О равен взятому
с соответствующим знаком произведению модуля силы на ее плечо:
m( ) .
O
FFh
r
(6.3)
Момент считается положительным, если сила стремится повернуть тело
вокруг точки О против хода часовой стрелки, и отрицательным по ходу
часовой стрелки.
Следовательно, для плоской
системы сил
12,3
, , , ...,
n
FF F F
rr r r
направление векторов
m( )
O к
F
r
r
(к = 1, 2,
…, n) перпендикулярных плоскости, в
которой лежат силы и точка О, можно
характеризовать знаком. Например, для
сил
12,
,
F
F
rr
, находящихся в плоскости
Оху (рис. 6.2), их алгебраические
моменты относительно точки В равны:
111
m( ) ,
B
FFh
r
222
m ( ) .
B
F
Fh
r
Пара сил. Момент пары
O
F
h
A
F
O
(
)
m
r
Рис. 6.1
B
y
O
x
h
1
h
2
A
1
A
2
F
1
F
2
Рис. 6.2

Система двух равных по модулю, параллельных и направленных в
противоположные стороны сил называется парой сил
F
F
rr
(рис. 6.3).
Плоскость, в которой лежат силы
F
r
и F
r
, называется плоскостью пары,
а кратчайшее расстояние d между линиями действия сил
плечом пары.
Пара сил не имеет
равнодействующей, так как
0 .RFF
rrr
Действие пары сил
F
,
F
r
на
абсолютно твердое тело сводится к
вращательному эффекту, который
характеризуется моментом пары.
Моментом пары называется
вектор
m dF
r
r
r
, (6.4)
модуль, которого равен произведению модуля одной из сил пары на ее плечо:
m dF
. (6.5)
Вектор
m
направлен перпендикулярно плоскости пары в ту сторону,
откуда пара видна, стремящейся повернуть тело против хода часовой
стрелки (рис. 6.3).
Свойства пар.
1. Момент пары равен сумме моментов сил пары относительно
произвольного центра (точки) О. Действительно, вычислим сумму моментов
сил пары
F
, F
относительно произвольного центра О (рис. 6.4).
Согласно (6.1)
m( ) m( )
( )
( ) m .
OO
FFrFrF
rFr F
rr FdF
rrrr
rr
rr
rr
rr
r
rr
r
rr
Следовательно, момент пары
m
век-
тор свободный, т. е. его можно
прикладывать в любой точке тела.
2. Момент пары равен моменту одной из сил пары относительно
точки приложения другой силы пары:
mm()
A
F
r
rr
. (6.7)
Приведем (без доказательства) следующие теоремы.
B
F
A
d
F
m
Рис. 6.3
B
F
A
d
F
m
r
r
O
Рис. 6.4
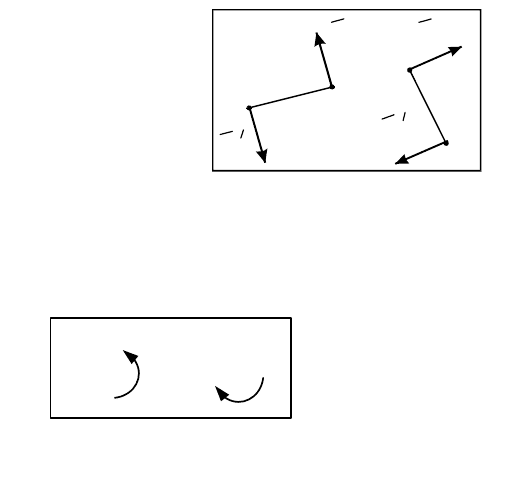
Теорема 1. Пары сил с геометрически равными моментами
эквивалентны.
Следствия:
1.
Пару сил, приложенную к твердому телу, можно заменить другой
парой в той же плоскости, если при этом не изменяется величина момента и
его направление:
111 2 22
mm dF dF
rr
rr
rr
или
11 2 2
.dFdF
rr
rr
2. Пару сил можно переносить в плоскость, параллельную плоскости
пары.
Теорема 2. Совокупность нескольких пар с моментами
n21
m ..., ,m ,m
эквивалентна одной паре, момент
М
r
которой равен геометрической сумме
моментов данных пар:
12
1
М m m .... m m .
n
n к
к
r
rr r r
(6.8)
Для пар, лежащих в одной плоскости, можно не прибегать к векторной
символике, а пользоваться понятием алгебраического момента пары.
Алгебраический момент пары равен взятому с соответствующим
знаком произведению модуля одной из сил пары на плечо пары:
m
F
d
. (6.9)
Знак «+» соответствует повороту тела в
плоскости под действием пары против хода
часовой стрелки, «
» по ходу часовой
стрелки.
Например, для пар, лежащих в одной
пло-скости, изображенных на рис. 6.5,
алгебраичес-кие моменты пар равны:
111 2 22
m , m .F d F d
Поскольку такие пары сил характеризуются только
величиной момента, то пары сил, лежащие в плоскости, часто
изображаются дуговыми стрелками, показывающими
направление поворота тела при действии пары (рис. 6.6).
Системой пар на плоскости называется совокупность
нескольких пар, действующих на тело.
d
1
F
1
F
1
F
2
F
2
d
2
Рис. 6.5
m
1
m
2
Рис. 6.6
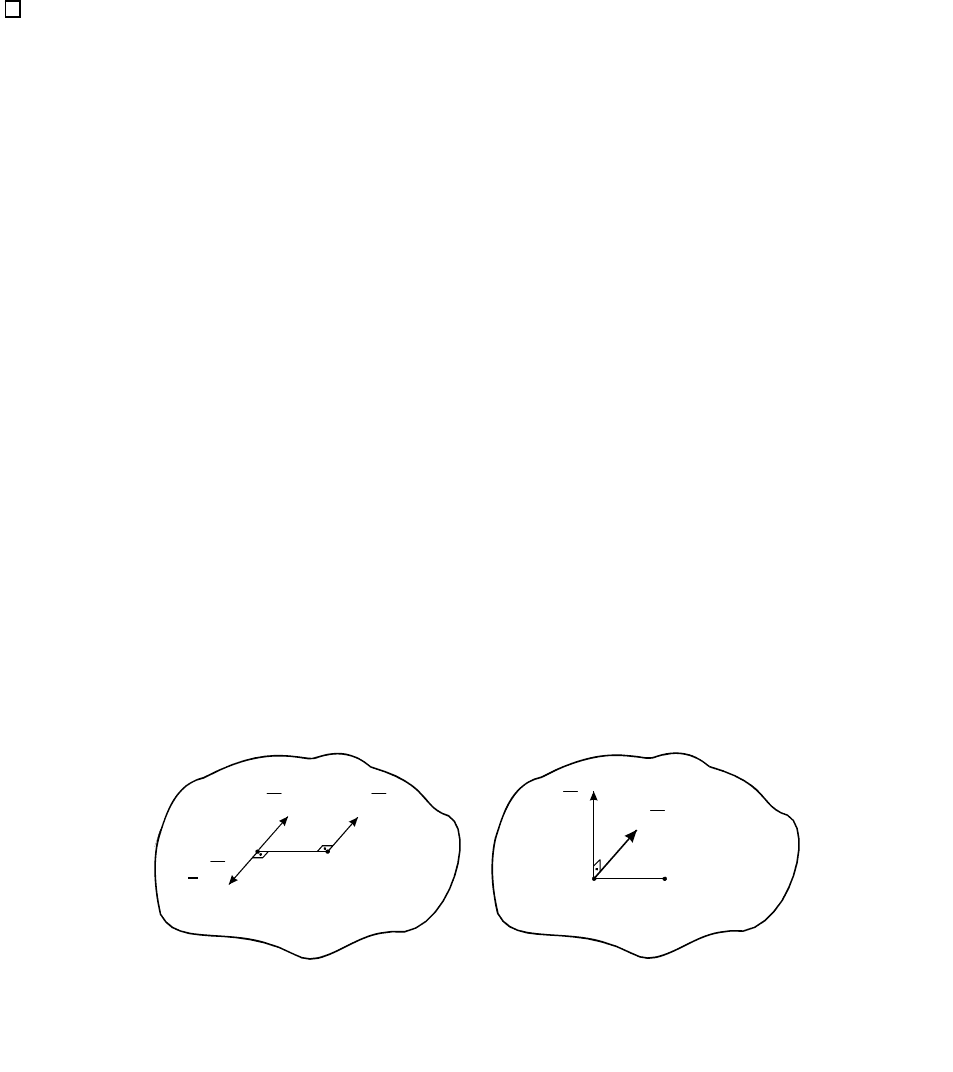
Систему пар сил на плоскости с моментами
12
m , m , ..., m
n
можно
заменить одной парой, момент М которой, согласно теореме 2 о сложении
пар (6.8) равен алгебраической сумме моментов данных пар:
12
1
М m m .... m m .
n
n к
к
(6.10)
Теорема о параллельном переносе силы
Теорема. Силу
F
r
, не изменяя ее действия на абсолютно твердое тело,
можно переносить из данной точки тела в любую другую, прибавляя при
этом пару с моментом, равным моменту переносимой силы относительно
точки, куда она переносится, т. е.
~ , mFF
rr
r
. (6.11)
Доказательство. Пусть в точке А твердого тела на него действует сила
F
. Согласно аксиоме 2 действие этой силы не изменится, если в любой точке
О тела приложить две уравновешенные силы
F
r
и
F
r
(рис. 6.7, а).
Данная система трех сил представляет собой силу
F
r
, но приложенную
в точке О, и пару сил
F
r
,
F
r
с моментом
mm()
O
OA F F
uuur
rr
rr
. (6.12)
Следовательно,
~ , mFF
rr
r
, но приложенной в точке О (рис. 6.7,
б), теорема доказана.
Теорема Пуансо
Задача о приведении системы сил
12,3
, , , ...,
n
FF F F
rr r r
к произвольному
центру (точке) О, т. е. о замене данной системы сил другой эквивалентной
F F
F
A
O
F
AO
m
а б
Рис. 6.7

более простой, решается применением теоремы Пуансо: любая система сил
12,3
, , , ...,
n
FF F F
rr r r
действующих на абсолютно твердое тело, при приведении
к произвольному центру О заменяется одной силой
R
r
, равной главному
вектору системы сил, приложенной в точке О, и парой сил с моментом
М
О
r
, равным главному моменту системы сил относительно центра (точки)
О:
12,3
, , , ..., ~ , M
nO
FF F F R
rr r r rr
. (6.13)
Доказательство. Пусть в точках А
1
, А
2
, …, А
n
твердого тела на него
действуют силы
12,3
, , , ...,
n
FF F F
rr r r
соответственно (рис. 6.8, а). Выберем
произвольную точку О за центр приведения и, пользуясь теоремой (6.11),
параллельно перенесем все силы в центр О, присоединяя пары с моментами
12
m , m ,..., m
n
rr r
(рис. 6.8, б), которые согласно (7.12) равны:
112 2
mm(), mm(),...,mm().
OOnOn
FF F
rr r
rr rr rr
(6.14)
Геометрически складываем в точке О силы
12,3
, , , ...,
n
FF F F
rr r r
и заменяем их
действие одной силой
12,3
1
..... ,
n
n к
к
RF F F F F
rr r r r r
(6.15)
приложенной в точке О (рис. 6.9). Используя теорему (6.8), совокупность пар
с моментами
12
m , m ,..., m
n
rr r
заменим одной эквивалентной парой с моментом
12
1
М m m .... m m ( ).
n
О n Ок
к
F
rr
rr r r
(6.16)
O
A
1
A
2
A
3
A
n
1
F
2
F
3
F
n
F
O
A
1
A
2
A
3
A
n
1
F
2
F
3
F
n
F
m
1
m
3
m
n
m
2
а б
Рис. 6.8

Вектор
R
r
, равный геометрической сумме всех сил, называется главным
вектором системы сил, а вектор
М
О
r
, равный геометрической сумме
моментов всех сил относительно центра О
главным моментом системы сил
относительно этого центра.
Следовательно, действие исходной системы сил
12,3
, , , ...,
n
FF F F
rr r r
на
твердое тело эквивалентно действию на него одной силы
R
r
и одной пары
с моментом
М
О
r
(рис. 6.9), т. е.
12,3
, , , ..., ~ , M
nO
FF F F R
rr r r rr
.
Теорема доказана.
Из (6.15) и (6.16) следует, что
вектор
R
r
от выбора центра О не
зависит, а вектор
М
О
r
при изменении
положения центра О может
изменяться по модулю и
направлению вследствие изменения
величин и направлений моментов
отдельных сил.
Отметим так же, что здесь сила
R
r
не является равнодействующей,
так как заменяет данную систему сил
не одна, а вместе с парой сил.
Следствие.
Две системы сил, имеющие геометрически равные главные векторы
и главные моменты относительно одного и того же центра, эквивалентны.
УСЛОВИЯ РАВНОВЕСИЯ
Для равновесия абсолютного твердого тела, находящегося под
действием произвольной системы сил, необходимо и достаточно, чтобы
главный вектор этой системы сил и её главный момент относительно
любого центра были равны нулю, т. е.
0R
r
,
М 0
О
r
. (6.17)
Условия (6.17) являются необходимыми, а если какое-нибудь из них не
выполняется, то исходная система сил не является уравновешенной, и при ее
действии тело будет двигаться.
Одновременно условия (6.17) являются и достаточными, поскольку при
0R
r
система сил может приводиться только к паре с моментом
М
О
r
, а так
как
М 0
О
r
, то имеет место равновесие тела.
O
A
1
A
2
A
3
A
n
R
M
O
Рис. 6.9
