Валькова Т.А. и др. Теоретическая механика

Подождите немного. Документ загружается.

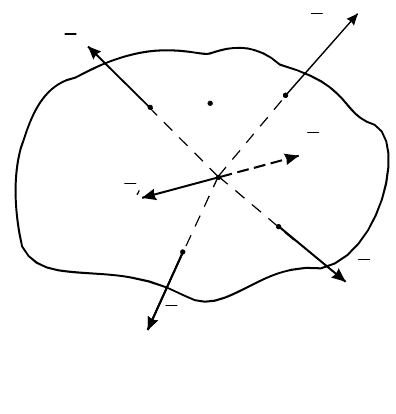
Теорема Вариньона

Теорема Вариньона. Если данная система сил имеет

равнодействующую, то момент равнодействующей относительно любого

центра О равен сумме моментов сил системы относительно того же

центра.

Доказательство. Пусть на абсолютно твердое тело действует система

сил

12,3

, , , ...,

FF F F

rr r r

, у которых линии действия пересекаются в точке С. Такая

система сил при приведении ее к точке С заменяется равнодействующей



приложенной в этой точке (рис. 6.10), так как

М 0



. Приложим в точке С

уравновешивающую силу







. Тогда система сил

12,3

, , , ...,

FF F F

rr r r

будет

уравновешенной





12,3

, , ,..., , , ~0,

FFF FR



rrr rr

и для нее, согласно (6.17)

М 0



или с учетом (6.16)

m( ) m( ) 0 .

Ок O









(6.18)

Но поскольку







, т. е. эти силы

направлены вдоль одной прямой в

противоположные стороны, то

m( ) m( ) .





(6.19)

Подставляя (6.19) в (6.18), получаем

m( ) m() 0

Ок O









или

m( ) m ( )

O Ок





. (6.20)

Теорема доказана. Теоремой Вариньона удобно пользоваться при

вычислении моментов сил.

ЛЕКЦИЯ 7

ПРОИЗВОЛЬНАЯ ПЛОСКАЯ СИСТЕМА СИЛ

Задача о приведении плоской системы сил

12,3

, , , ...,

FFF F

rrr r

к точке

(центру) О решается применением теоремы Пуансо (6.13).

Рис 6

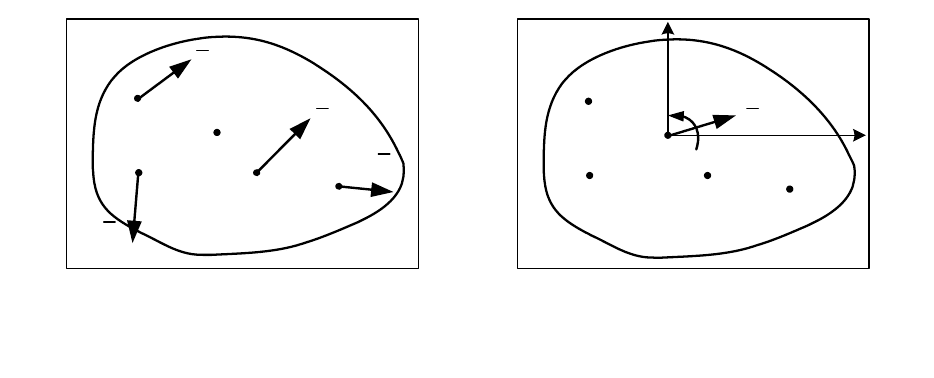
Согласно этой теореме плоская произвольная системы сил

, ,FF

, ...,

(рис. 7.1, а) при приведении к точке О, лежащей в плоскости их

действия, заменяется одной силой

123

..... ,

n к

RF F F F F



    



rr r r r r

(7.1)

приложенной в точке О, и парой сил с моментом

12 к

к 1

М m ( ) m ( ) ...+ m ( ) m ( )

О OO OnO

FFF



 



rr r r

. (7.2)

Вектор



, равный геометрической сумме всех сил, называется главным

вектором системы сил, а момент

пары, равный сумме алгебраических

моментов всех сил относительно точки О,

 главным моментом системы сил

12,3

, , , ...,

FFF F

rrr r

относительно этой точки (рис. 7.1, б).

Следовательно, действие данной системы сил

12,3

, , ,...,

FFF F

rrr r

на

твердое тело эквивалентно действию на него одной силы



, приложенной в

точке О, и одной пары, лежащей в плоскости действия исходной системы

сил, с алгебраическим моментом

(рис. 7.1).

Из (7.1) и (7.2) вытекает, что вектор



от выбора центра О не зависит,

а момент

пары при изменении положения точки О может изменяться

вследствие изменения величин и знаков моментов отдельных сил.

Отметим, что модуль и направление главного вектора



вычисляются

по формулам (5.9) – (5.11). Однако эта сила не является равнодействующей,

так как заменяет данную систему сил

12,3

, , , ...,

FFF F

rrr r

не одна, а вместе

с парой сил.

Рассмотрим частные случаи приведения плоской системы сил.

а б

Рис. 7.1

1. Если

0R 

, а



, то плоская система сил приводится к равно-

действующей, приложенной в точке О.

2. Если

0R



, а

М 

, то плоская система сил приводится к паре сил.

3. Если

0R 



, то плоская система сил приводится к равно-

действующей, приложенной в точке О

, отстоящей от точки О на расстояние

OO h

R

4. Если

0R



, и

М 

, то плоская система сил является уравновешенной.

Условия равновесия для плоской системы

Для равновесия абсолютного твердого тела, находящегося под

действием плоской произвольной системы сил, необходимо и достаточно,

чтобы главный вектор этой системы сил и ее главный момент

относительно любой точки на плоскости были равны нулю, т. е.

0R



0М



. (7.3)

Условия (7.3) являются необходимыми достаточными условиями

равновесия тела под действием плоской произвольной системы сил

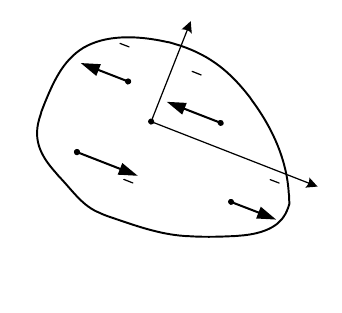
Если тело находится в равновесии под действием произвольной

плоской системы сил

12,3

, , , ...,

FFF F

rrr r

(рис. 7.2), то из (7.3) с учетом (5.8),

(5.9) и (7.2) следуют три уравнения равновесия:

11 1

0, 0, m ( ) 0.

nn n

кx кy Ок

кк к

FF F

 





 

(7.4)

Для равновесия твердого тела под

действием произвольной плоской системы сил

необходимо и достаточно, чтобы сумма

проекций сил на каждую из двух координатных

осей и сумма моментов относительно любой

точки, лежащей на плоскости действия сил,

были равны нулю.

Уравнения (7.4) называются

первой (основной) формой

аналитических условий равновесия для плоской произвольной системы

сил.

Отметим, что в математическом отношении система уравнений

равновесия (7.4) будет проще, если в ней в качестве точки О, относительно

которой составляется третье уравнение моментов, выбрать точку

пересечения линий действия двух искомых сил.

Вторая форма уравнений равновесия эквивалентная системе (7.4)

имеет вид

Рис. 7.2

111

0 , m ( ) , m ( ) 0.

nnn

кx Ак Вк

ккк

FFF







(7.5)

При этом ось О

х не перпендикулярна прямой АВ, проходящей через точки

плоскости Оху, относительно которых составляются уравнения моментов.

Третья форма уравнений равновесия для плоской произвольной

системы сил не содержит уравнений проекций сил на оси:

11 1

m ( ) , m ( ) 0, m ( ) 0.

nn n

Ак Вк Ск

кк к

FF F

 



 

rr r

(7.6)

При этом предполагается, что точки А, В, и С плоскости Оху, относительно

которых составляются уравнения моментов, не лежат на одной прямой.

В случае системы параллельных сил

12,3

, , , ...,

FF F

rrr r

, лежащих в

плоскости Оху, выберем ось Ох параллельно силам (рис. 7.3). Тогда в (7.4)

останется два уравнения равновесия:

0 , m ( ) 0 .

кx Ок

кк





(7.7)

Уравнения (7.7) являются первой формой

аналитических условий равновесия для

плоской системы параллельных сил

Для равновесия твердого тела под

действием плоской системы параллельных сил

необходимо и достаточно, чтобы сумма

проекций сил на ось, параллельную силам, и

сумма моментов относительно любой точки,

лежащей на плоскости действия сил, были

равны нулю.

Вторая форма уравнений равновесия для плоской системы

параллельных сил не содержит уравнения проекций сил на ось:

m ( ) , m ( ) 0.

Ак Вк

кк







(7.8)

При этом предполагается, что точки А, В, плоскости Оху, относительно

которых составляются уравнения моментов, не лежат на прямой

параллельной данным силам, например, прямая АВ должна быть не

параллельна оси Ох для сил, изображенных на рис. 7.3.

Рис. 7.3

Теперь рассмотрим равновесия тела под

действием системы пар сил, лежащих

в плоскости Оху, с моментами

m , m , ..., m

(рис. 7.4). Согласно

теоремы (6.9) ее можно заменить одной

парой, момент М которой равен

алгебраической сумме моментов данных

пар. При равновесии М = 0, и,

следовательно,

m=0

к



Это уравнение выражает условие равновесия твердого тела, находящегося

под действием системы пар.

Распределенные силы

При расчетах иногда встречаются нагрузки, распределенные вдоль

поверхности твердого тела по определенному закону.

1. Простейшим примером распределенных сил, лежащих в одной

плоскости, является

равномерно-распределенная нагрузка (рис. 7.4, а).

Такая система распределенных сил характеризуется постоянной по

величине интенсивностью q

− значением силы, приходящейся на единицу

длины нагруженного участка АВ. Размерность интенсивности нагрузки

[q] =

Н/м.

При статических расчетах эту систему параллельных сил можно

заменить равнодействующей



, приложенной в середине отрезка АВ (рис.

7.4, а), модуль которой равен

Qqd





. (7.9)

Рис. 7.4

а б

Рис. 7.4

2. Силы, распределенные вдоль отрезка АВ по линейному закону.

Для этих сил интенсивность q

является переменной величиной,

изменяющейся от нуля до максимального значения

(рис. 7.4, б).

Равнодействующая

таких сил равна по модулю площади треугольника

АВС

Qqd





(7.10)

Линия действия этой силы проходит через центр тяжести треугольника, т. е.

на расстоянии, d/3

от основания ВС треугольника АВС (рис. 7.4, б).

Равновесие системы тел

Статический расчет системы тел сводится к рассмотрению условий

равновесия конструкций, состоящих из тел, соединенных какими-либо

связями. Связи, соединяющие части конструкции, называются внутренними.

Связи, скрепляющие конструкцию с другими не входящими в нее телами,

являются внешними.

При решении задач статики реакции связей входят в число

неизвестных, которые необходимо определить из уравнений

равновесия.

Системы тел, для которых число неизвестных реакций связей равно числу

уравнений равновесия, называются статически определимыми. Системы тел,

для которых число неизвестных реакций связей больше количества

уравнений равновесия, называются статически неопределимыми.

Если при отбрасывании внешних связей (опор) конструкция остается

жесткой, то для нее задача о равновесии решается как для абсолютно

твердого тела (при действии произвольной плоской системы сил число

неизвестных реакций, согласно (7.4), не должно быть больше трех).

Если при отбрасывании внешних связей конструкция не остается

жесткой, то наиболее рациональным способом решения подобных задач

является расчленение на отдельные тела и составление уравнений равновесия

для каждого из тел в отдельности.

Для конструкции

, состоящей из n тел, на каждое из которых действует

произвольная плоская система сил, получим 3n

уравнений равновесия,

позволяющих найти 3n

неизвестных.

Рис. 7.5

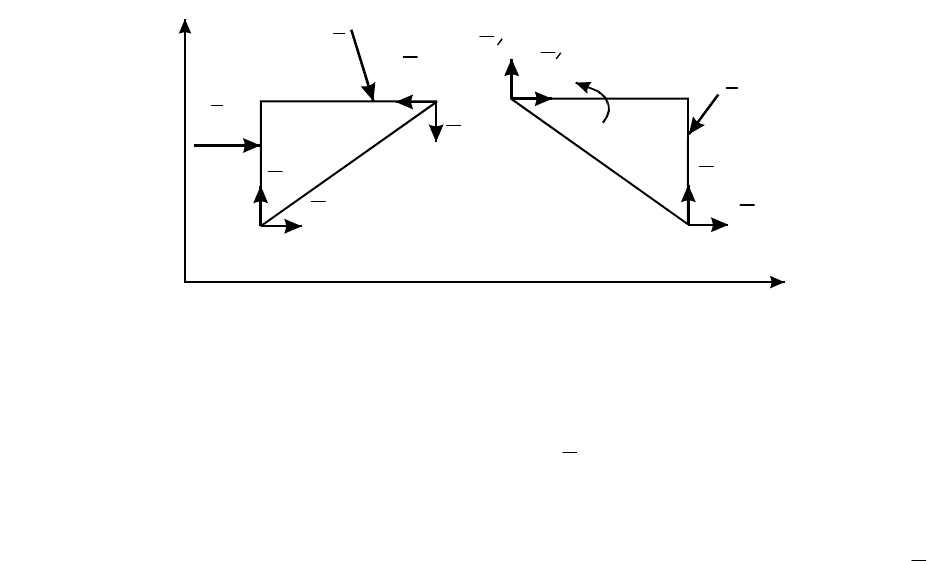
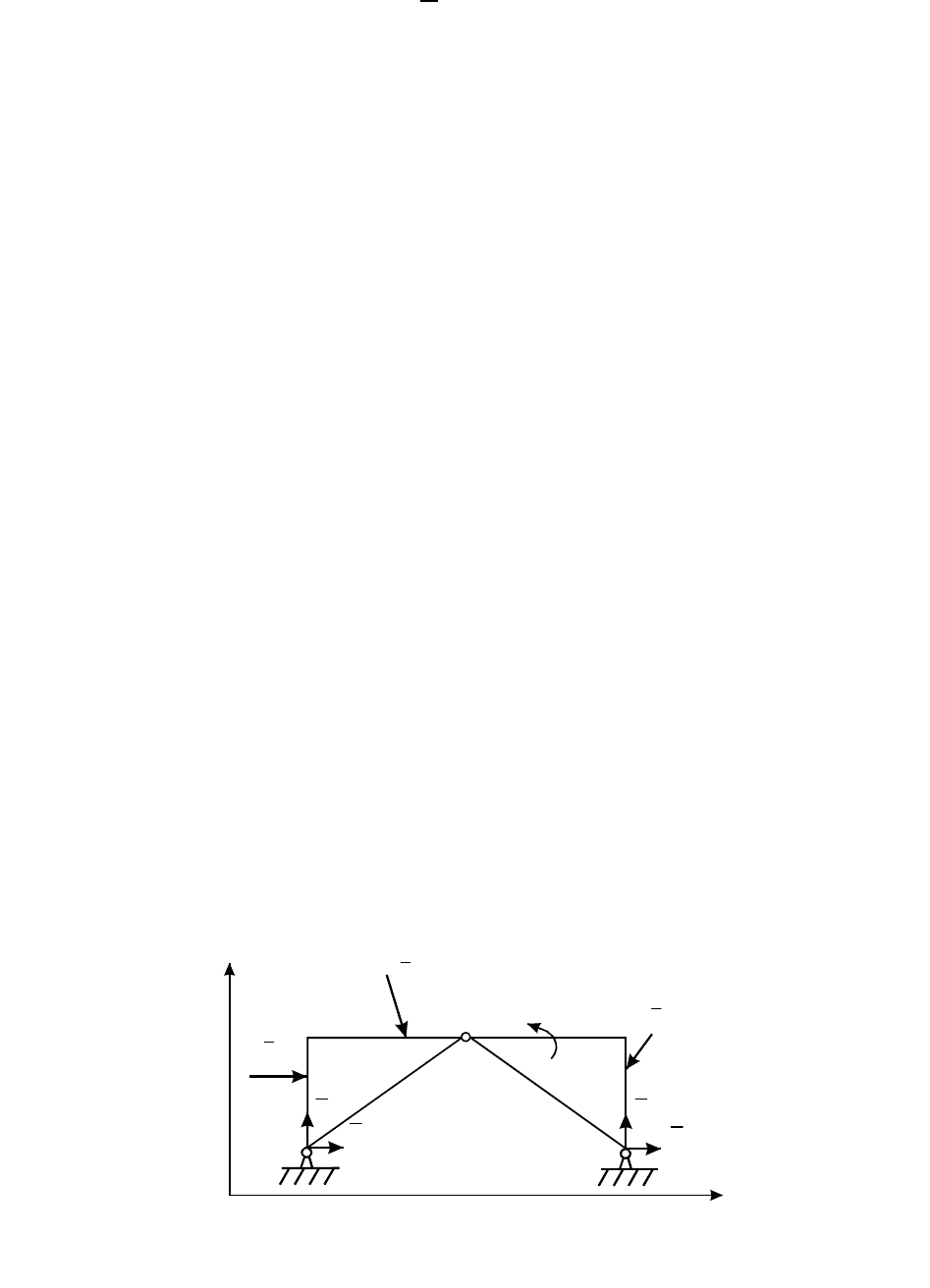
Например, если отбросить опоры А и В трехшарнирной арки (рис. 7.5),

то она не будет жесткой: ее части могут поворачиваться вокруг

соединительного шарнира С. На основании принципа отвердивания (аксиома

5) система сил, действующая на арку, должна удовлетворять условиям

равновесия для твердого тела.

Для трехшарнирной арки АВС, находящейся под действием

произвольной плоской

системы сил, получим три уравнения равновесия (7.4)

с четырьмя неизвестными

, , ,

ABB

YX Y

rrr

. Условия (7.4), являясь

необходимыми, не будут для деформируемого тела достаточными,

так как из них нельзя найти все неизвестные реакции.

Поэтому для определения реакций внешних связей

, , ,

ABB

YX Y

rrr

расчленим конструкцию по соединительному шарниру С на две части и

рассмотрим равновесие каждой из частей в отдельности (рис. 7.6).

При действии на трехшарнирную арку произвольной плоской системы

сил для каждой части можно записать три уравнений равновесия (7.4):

для АС

111

0; 0; m ( ) 0;

nnn

кx ку А к

ккк

FF F



 



(7.11)

для СВ

111

0; 0; m ( ) 0.

nnn

кx ку B к

ккк

FF F



 



Добавляя к уравнениям (7.11) согласно аксиоме 4 статики условие

равенства модулей реакций в соединительном шарнире С (

СССС

XYY





), получим систему шести уравнений (7.11) с шестью

неизвестными

, , , , ,

AA BB СС

YX Y X Y

Следовательно, трехшарнирная арка АВС является статически

определимой системой, для которой после решения системы уравнений

(7.11) можно найти как реакции внешних связей

, , ,

ABB

YX Y

, так и

реакции внутренних связей

СС

Рис. 7.6

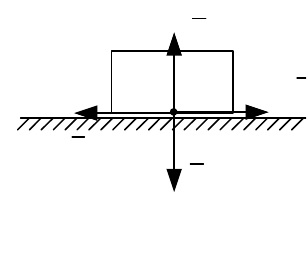
Трение сцепления и скольжения

При стремлении сдвинуть тяжелое тело по поверхности другого тела

под действием горизонтальной силы



в плоскости их соприкосновения

возникает сила сцепления

сц



(сила трения покоя), препятствующая

движению тел друг относительно друга (рис. 7.7).

Возникновение трения обусловлено, прежде всего, шероховатостью

поверхностей, создающей сопротивление перемещению, и наличием

сцепления у прижатых друг к другу тел.

Приложенная к телу сила сцепления

сц



направлена в сторону, противоположную той,

куда действующие на тело силы стремятся его

сдвинуть. Причем в положении равновесия

сц

F Q





. (7.12)

Тело останется в покое при увеличении силы



от нуля до некоторого

максимального значения

пр



, при котором тело еще не движется. При этом

согласно (7.12) сила трения покоя будет принимать значения от нуля до

максимального значения

пр



, называемого предельной силой трения, т. е.

прсц



0

(7.13)

Экспериментально было установлено, что предельная сила трения

пр



численно равна произведению коэффициента сцепления (статического

коэффициента трения) на величину нормального давления, или нормальную

реакцию



поверхности:

N fF

cцпр



. (7.14)

Коэффициент сцепления

cц

 величина безразмерная, зависящая от

материала соприкасающихся тел, состояний поверхностей контакта,

температуры, влажности и т. п. Значение коэффициента сцепления

cц

определяется опытным путем и для используемых в технике материалов его

величина, как правило, меньше единицы (например,

cц

= 0,40,7 для пары

дерево по дереву; 0,15

0,25 для пары метал по металлу; 0,027 для пары сталь

по льду.

Значение предельной силы трения

пр



не зависит от размеров

соприкасающихся при трении тел.

сц

Рис. 7.7

Равновесие, при котором сила сцепления достигает максимального

значения

пр



, называется состоянием предельного равновесия, при котором

величина сдвигающей силы

N fF Q

сцпр



При дальнейшем увеличении модуля

силы

пр

F Q 

тело начнет двигаться

(скользить) по поверхности.

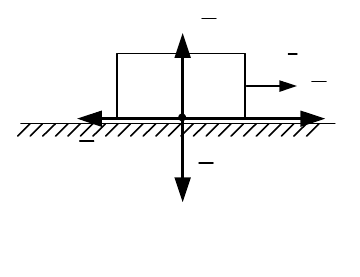
При скольжении тела по шероховатой

поверхности к нему приложена сила трения

скольжения

тр



(рис. 7.8). Направление этой

силы противоположно направлению скорости



тела, модуль силы трения скольжения

определяется произведением коэффициента трения на величину нормальной

реакции:

N fF

тр



. (7.15)

Здесь

 коэффициент трения скольжения также является величиной

безразмерной, определяемой опытным путем. Значение коэффициента

зависит от материала и физического состояния трущихся поверхностей,

удельного давления, а также в некоторой степени от скорости движения

одного тела по отношению к другому. Обычно с увеличением относительной

скорости взаимодействующих тел коэффициент

сначала убывает от

значения

cц

, а затем сохраняет постоянное значение, т. е.

cц



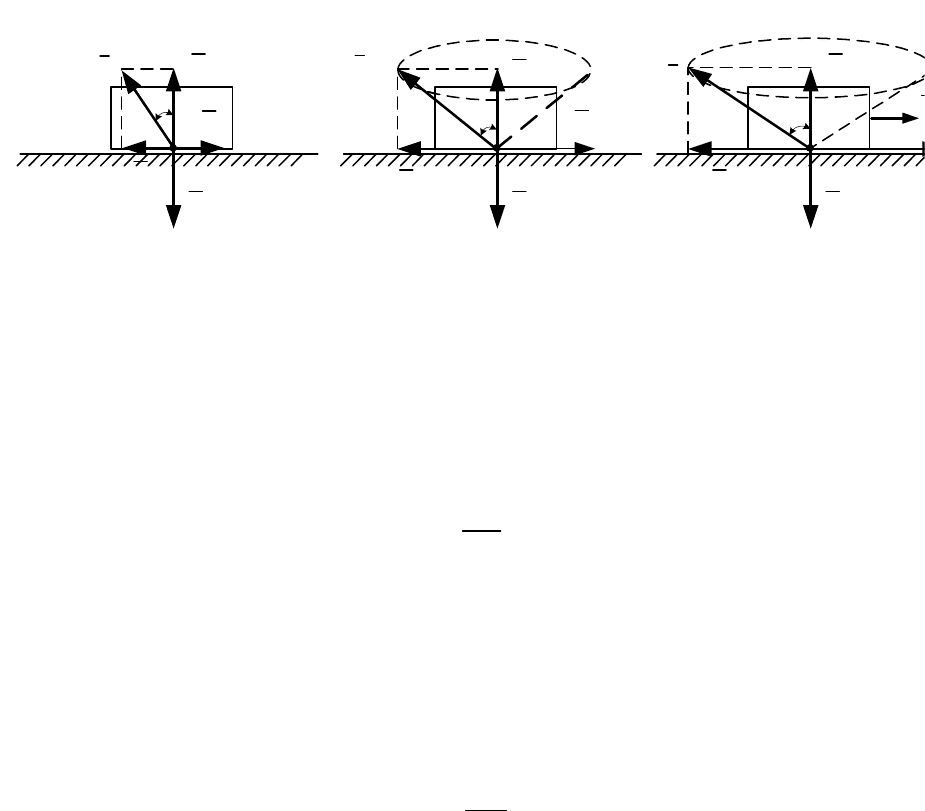
Реакция



шероховатой поверхности имеет две составляющие:

нормальную реакцию



и перпендикулярную ей силу сцепления

сц



при

равновесии (рис. 7.9, а) (или силу трения скольжения при движении (рис. 7.9,

в)). Поэтому реакция



будет всегда отклонена от нормали к поверхности на

некоторый угол

. Согласно (7.13) при равновесии тела угол  может

принимать значения от нуля до некоторого предельного значения

сц



(

сц

0

которое соответствует положению предельного равновесия (рис.

7.9, б).

тр

Рис. 7.8

Это максимальное значение

сц



называется углом сцепления (углом

трения покоя). На рис. 7.9, б видно, что

tg ,

пр

сц сц

 

(7.16)

или

aretg .

сц сц





(7.17)

При движении тела реакция



будет всегда составлять с нормалью к

поверхности угол, называемый углом трения



тр

. (рис. 7.9, в), причем

тр





, (7.18)

или

aretg .

тр





(7.19)

Конус с вершиной в точке касания тел, образующая которого

составляет угол сцепления



сц

с нормалью к поверхностям тел, называется

конусом сцепления (рис. 7.9, б).

Конус с вершиной в точке касания тел, образующая которого

составляет с нормалью к поверхностям тел угол трения



тр

, называется

конусом трения (рис. 7.9, в).

Если коэффициенты

cц

по всем направлениям поверхности

контактирующих тел одинаковы, то соответствующие конусы сцепления и

трения будут круговыми (см. рис. 7.9).

Если же коэффициенты

cц

в различных направлениях поверхности

контактирующих тел изменяются по величине, то соответствующие конусы

будут иметь сложную форму.

сц



тр



тр

пр



сц

max

пр

а б в

Рис. 7.9