Валькова Т.А. и др. Теоретическая механика

Подождите немного. Документ загружается.





sin γ 2cosγ sin γ sin γ cosβ cos γ sinβp B bpB k B h 

. (12.26)

Приравнивая коэффициенты при

sin

cos

в левой и правой частях

уравнения (12.26), получаем систему алгебраических уравнений

относительно постоянных В и

( ω ) cosβ,

2 ω sinβ.

kBh

bB h











Отсюда находим

222 22

( ω )4ω





(12.27)

2 ω

tgβ .





(12.28)

Подставляя (12.27) и (12.28) в (12.24) получим частное решение

неоднородного уравнения (12.21),

222 22

sin(ωδβ)

( ω )4ω





(12.29)

Следовательно, общее решение (12.22) дифференциального уравнения

(12.21) имеет вид





222 22

sin α sin(ωδβ)

( ω )4ω

xAe k bt t



 



. (12.30)

Постоянные интегрирования

, входящие в первое слагаемое

(12.30), можно определить подстановкой в (12.30) и в выражение для

соответствующей скорости

начальных условий движения материальной

точки (11.5).

Согласно (12.30) прямолинейные колебания точки являются сложными

и складываются из собственных затухающих колебаний (первое слагаемое) и

вынужденных колебаний (второе слагаемое).

Собственные колебания по истечении некоторого промежутка времени

, называемого временем установления, довольно быстро затухают, и

характер колебаний системы будут определять только вынужденные

колебания.

Например, если собственными

колебаниями (12.23) можно

пренебречь, начиная с момента

времени, когда их амплитуда станет

меньше

0,01 B

, то время

установления

можно определить

из равенства

0,01





, откуда

1 100



. (12.31)

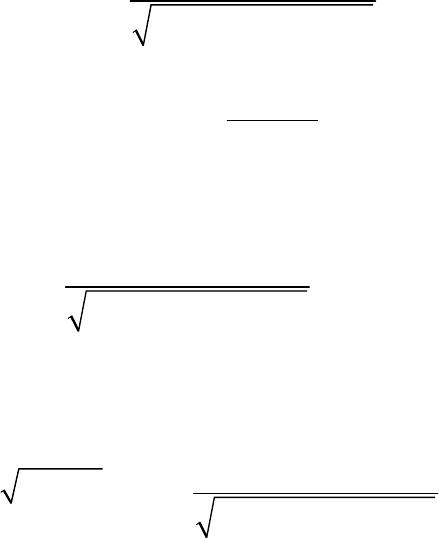
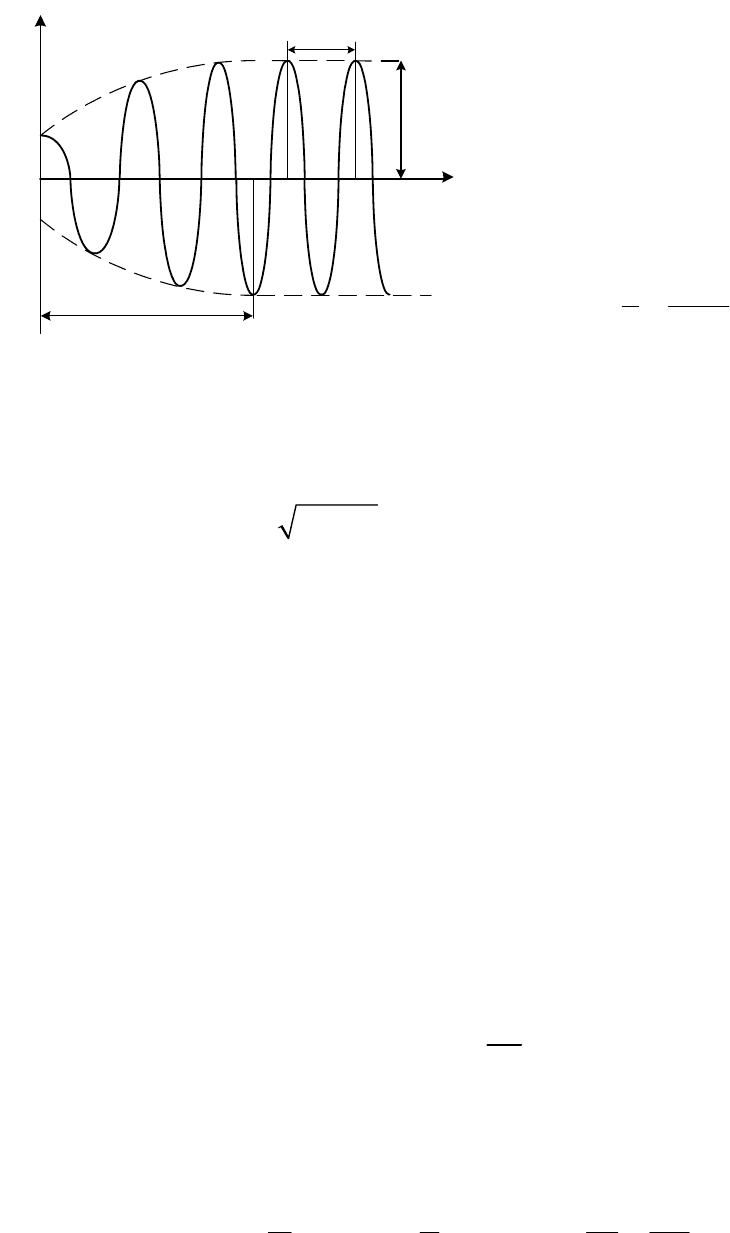
Одна из возможных картин установления колебаний точки,

происходящих по закону (12.30), показана на рис. 12.4. Очевидно, что при

других начальных условиях движения и иных соотношениях между

частотами

*22

kkb

характер колебаний в интервале времени

0 tt

может быть другим.

Однако во всех случаях при

tt

точка будет совершать только

вынужденные колебания по закону (12.29)

sin(ωδβ)xB t





. (12.32)

Следовательно, вынужденные колебания точки представляют собой

гармонические колебания с амплитудой В, определяемой формулой (12.27),

и частотой

, равной частоте возмущающей силы

При наличии сопротивления вынужденные колебания сдвинуты по

фазе относительно возмущающей силы на величину

(12.28).

Период установившихся колебаний будет равен периоду вынужденных

колебаний

2π

T 

(12.33)

Рассмотрим частные случаи вынужденных колебаний точки. Для этого

введем безразмерные параметры:

ст

λ , η , δ

bhH

kk kc

 

. (12.34)

Тогда с учетом (12.33) формулы (12.27) и (12.28) для амплитуды В и сдвига

фаз

принимают вид

Рис. 12.4

ст

22 2 2

(1 λ )4ηλ

B 



(12.35)

2η λ

tgβ .

1 λ





(12.36)

1. Если частота возмущающей силы

много меньше собственной

частоты (

ω < k

), то, раскладывая (12.35) и (12.36) в ряд Тейлора по степеням

безразмерного параметра малости

λ << 1

и ограничиваясь квадратичными

слагаемыми, получаем

ст

δ ,

tgβ 0.



(12.37)

Здесь

ст

δ 

величина статического отклонения точки М от положения

равновесия О под действием постоянной силы, равной по величине

Колебания в этом случае происходят с амплитудой равной статическому

отклонению

ст

и сдвигом фаз

β 0



, т. е. фазы вынужденных колебаний и

возмущающей силы

все время совпадают.

2. Если частота возмущающей силы

много больше собственной

частоты (

ω k

), то



. Из (12.35) следует, что величина амплитуды В

вынужденных колебаний становится малой. Если считать сопротивление

малым (



), то для оценки В можно получить приближенную формулу

ст 0

λω

B 

. (12.38)

Этот случай представляет наибольший интерес для проблем виброзащиты

сооружений, механизмов, машин, и т. п.

3. Если частота возмущающей силы

совпадает с собственной

частотой (

ω k

), то величина амплитуды В вынужденных колебаний точки

достигает максимального значения

ез

, и имеет место явление, называемое

резонансом.

Действительно, представим в (12.35) амплитуду В как функцию

безразмерного параметра

ξλ



ст

222

(ξ) .

(1 ξ)4ηξ

B 



(12.39)

Из (12.39) видно, что амплитуда В вынужденных колебаний будет достигать

максимального значения

рез

, если величина

(ξ)(1ξ)4ηξf  

, стоящая

в знаменателе, имеет минимум. Решая уравнение

(ξ)2(1ξ 2η )0f





 

и проверяя условие на минимум функции

(ξ)

(ξ)20f







находим,

min

ξ 12η

. Отсюда получаем, что при частоте возмущающей

силы равной

рез

ω 2kb

(12.40)

амплитуда В вынужденных колебаний достигает максимального значения.

Если сопротивление мало (

η 1



2kb

), то, раскладывая (12.40) в ряд

по малому параметру



, получаем, что резонанс имеет место, если

рез

ω (1 )





В этом случае при резонансе амплитуду вынужденных колебаний и

сдвиг фаз можно оценить по формулам:

ст 0

рез рез

рез

δπ

, β .

2η 2 ω 2

 

(12.41)

Из (12.41) следует, что при малом сопротивлении амплитуда

ез

вынужденных колебаний может достигать довольно больших значений.

Из (12.40) имеем, что при достаточно большом сопротивлении среды

(

2kb

) резонанс выражен слабо (амплитуда

ез

невелика), а при

2kb

резонанс вообще не возникает.

Проведенные исследования вынужденных колебаний приводят к

следующим выводам:

1) амплитуда В вынужденных колебаний и сдвиг фазы

от начальных

условий движения материальной точки не зависят;

2) вынужденные колебания при наличии сопротивления не затухают;

3) частота и период вынужденных колебаний равны частоте и пери-

оду возмущающей силы

;

4) даже при больших значениях возмущающей силы

вынужденные

колебания точки около положения равновесия будут малыми, если частота

этих колебаний

будет много больше собственной частоты

;

5) даже при малой возмущающей силе

вынужденные колебания

точки перестают быть малыми, если сопротивление среды мало, а частота

вынужденных колебаний

близка к собственной частоте

(резонанс).

ЛЕКЦИЯ 13

ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ ТОЧКИ

Рассмотрим материальную точку массой m, движущуюся под

действием сил взаимодействия с другими телами

, ,...,

rr r

относительно

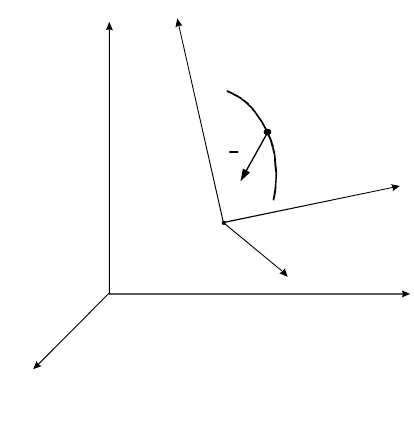
подвижных осей Охуz, которые произвольно перемещаются относительно

инерциальной (неподвижной) системы отсчета

OXYZ

(на рис. 13.1





). Найдем зависимость между относительным ускорением точки и

действующими на нее силами.

В инерциальной системе отсчета

OXYZ

основной закон динамики для

абсолютного движения точки (10.4) имеет вид

a к

ma F





. (13.1)

По теореме Кориолиса о сложении ускорений при сложном движении точки

(4.22) имеем

Crеa

aaaa







. (13.2)

Подставляя (13.2) в (13.1) и введя

обозначение для относительного

ускорения



, получаем

е C к

ma ma ma F



 



rrr

или

кеC

ma F ma ma







rrr

(13.3)

Так как второе и третье слагаемые правой

части (13.3) имеют размерность силы, введем следующие обозначения.

Вектор

Ри

с.

ее

ma

(13.4)

назовем переносной силой инерции, а

Ф 2 ω

СС er

ma m V



 

(13.5)



кориолисовой силой инерции.

Согласно (13.4) и (13.5) векторы

направляются противоположно

переносному ускорению

и ускорению Кориолиса

соответственно.

Тогда с учетом (13.4) и (13.5) выражение (13.3) принимает вид

ФФ

ке C

ma F







rr r

. (13.6)

Уравнение (13.6) называется основным законом динамики

относительного движения точки.

Сопоставляя (13.1) и (13.6), приходим к выводу: «Все уравнения

механики относительного движения точки составляются также как

уравнения абсолютного движения, если к действующим на точку силам

, ,...,

FF F

rr r

прибавить переносную

и кориолисову

силы инерции».

Согласно (13.6) в неинерциальной системе отсчета Охуz материальная

точка получает ускорение, как за счет действующих сил

, ,...,

FF F

rr r

, так

и в результате ускоренного движения самой системы отсчета, т. е. появление

переносной

и кориолисовой

сил инерции имеет кинематическую

причину.

Частные случаи.

1. Если подвижная система координат Охуz движется поступательно, то

угловая скорость переносного движения точки





и согласно (13.5)

Ф 0



. Тогда закон относительного движения точки имеет вид:

ке

ma F







. (13.7)

2. Если подвижные оси координат Охуz перемещаются поступательно

равномерно и прямолинейно, то переносная и кориолисова силы инерции

равны нулю (

Ф 0



Ф 0



), и закон относительного движения точки имеет

тот же вид, как и закон относительно неподвижных осей (13.1). Поэтому

такая подвижная система отсчета Охуz будет инерциальной.

Отсюда следует

принцип относительности классической механики,

установленный Галилеем: «Никаким механическим экспериментом нельзя

обнаружить, находится ли данная система отсчета в покое или совершает

поступательное, равномерное и прямолинейное движение».

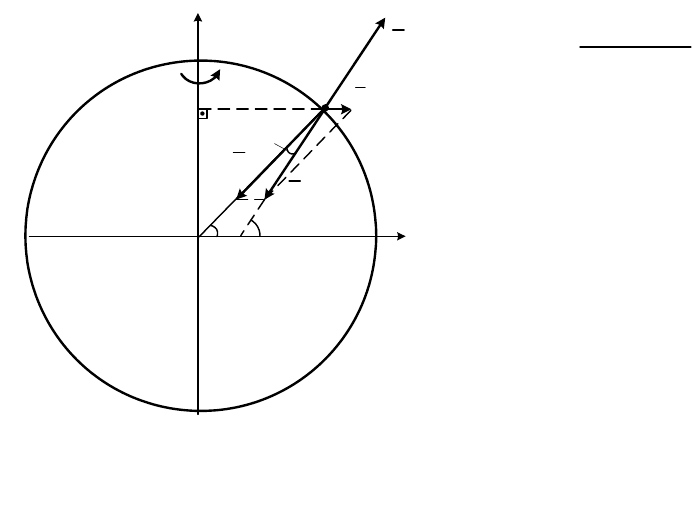
3. Если материальная точка по отношению к подвижной системе

отсчета Охуz находится в покое, т. е. для нее



V 

, и поэтому

Ф 0



. Тогда формула (13.6) принимает вид:

Ф 0

ке









(13.8)

Уравнение (13.8) называется уравнением относительного равновесия (покоя)

точки.

Сравнивая (13.8) с уравнением равновесия в инерциальной системе

отсчета (5.12) приходим к выводу, что уравнения относительного равновесия

составляются так же, как уравнения равновесия в неподвижных осях, если

к действующим на точку силам взаимодействия с другими телами добавить

переносную силу инерции.

Относительное равновесие тел вблизи поверхности Земли

Рассмотрим материальную точку В массой m, находящуюся в покое на

поверхности Земли (радиус

6370 кмR



). Связанная с Землей подвижная

система отсчета не является инерциальной, поскольку она совершает один

оборот вокруг своей оси за 24 ч с угловой скоростью

-1

0,000073 c

24 60 60



 



Изучим вопрос о влиянии такого

довольно медленного вращения Земли

на равновесие тела (материальной

точки) на ее поверхности.

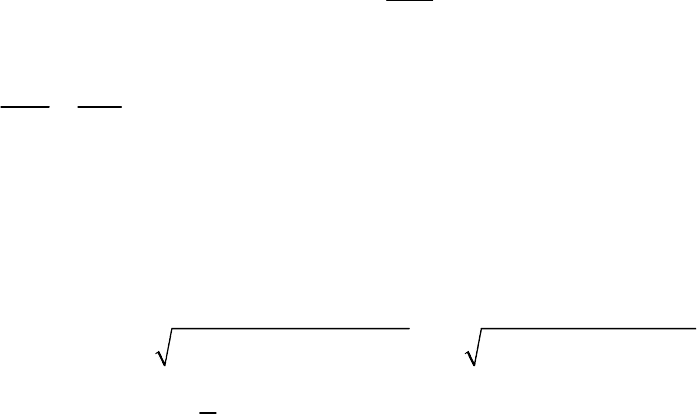
В состоянии покоя на точку В

действуют: сила тяготения

(

т 0

Fmg



, где

9,82 м/cg 

гравитационное ускорение); переносная

сила инерции

ma

обусловленная равномерным

вращением Земли (





cos





, где угол 



геоцентрическая широта); и реакция опоры

(рис. 13.2). Тогда в этом случае

уравнение относительного равновесия (13.8) принимает вид









Рис. 13.2

Ф 0





rr r

. (13.9)

Из рис. 13.2 следует, что действие тела В на опору выражается силой

N

, называемой силой тяжести. Таким образом, сила тяжести

является результирующей силы тяготения

и переносной силы инерции

, обусловленной вращением Земли, т. е.





rrr

. (13.10)

Направление вектора

определяет линию отвеса (вертикали) в данной

точке земной поверхности, составляющей с плоскостью экватора угол ,

называемый географической широтой ( =  + ). Плоскость

перпендикулярная силе

является горизонтальной плоскостью. Модуль

силы тяжести

mg

называется весом, где



ускорение свободного

падения.

Спроецируем (13.10) на оси декартовой системы координат Сху

(рис.13.2):

cos cos Ф ,

sin sin ,





или, подставляя значения модулей сил, после не сложных преобразований

получим

cos (1 / )cos ,

sin sin .

ggRg



 

 

(13.11)

Из (13.11) находим

tg tg







где

289



  

. Поэтому при решении инженерных задач обычно

полагают, что





0

и силу тяжести

направляют по радиусу R Земли

к ее центру С.

Из (13.10) следует, что вес Р и значение ускорение свободного падения

зависят от широты  . Действительно, из (13.11) находим



222 22

sin (1 ) cos 1 ( 2 )cos =

= 1 2 cos ... ,

gg g





  





или, ограничиваясь в разложении первой степенью малости по , получим





1cosgg



 

. (13.12)

Отсюда вытекает, что наименьшее значение вес тела

mg

имеет на

экваторе ( = 0, переносная сила инерции достигает максимальной величины

max

Ф 0,0034



), так как





min 0 0

19,78 м/c ,gg g R

наибольшее



на полюсе ( = /2, переносная сила инерции обращается в

нуль

Ф 0



), поскольку

max 0

9,82 м/cgg

В случае равновесия тела на поверхности Земли под действием

системы сил, выделяя из их числа силу тяготения

кк

FFF



rrr

уравнение относительного покоя (13.8) принимает вид

+Ф 0

к e







rrr

или с учетом (13.10) получим уравнение

FP



(13.13)

такое же, как если бы система отсчета, связанная с Землей считалась

неподвижной.

Следовательно, при составлении уравнений равновесия тел по

отношению к Земле дополнительных поправок на вращение Земли вводить не

надо.

Относительное движение тел вблизи поверхности Земли

Теперь рассмотрим, как влияет вращение Земли при движении

материальной точки В по ее поверхности (рис. 13.3). Выделяя из числа

действующих на нее сил силу тяготения (

кк

FFF







rrr

), запишем

основной закон динамики относительного движения (13.6)

+ФФ

к eC

ma F F 



rrr r

или с учетом (13.10)

к C

ma F P



rrr

. (13.14)

Из сравнения (13.14) с (13.1) следует, что когда при составлении

уравнений движения, оси, связанные с Землей, считают неподвижными, то

пренебрегают учетом только кориолисовой силы инерции, модуль которой

согласно (13.5) равен

Ф 2 ω sin(ω )

С er er

mV V

Поскольку угловая скорость Земли

-1

ω 0,000073 c



очень мала, то при малой

величине относительной скорости

, кориолисовой силой инерции

в (13.14) можно пренебречь, (например, для артиллерийского снаряда

700 м/c

V 

и при

(ω )90

V

модуль кориолисовой силой инерции



1 % Р). Поэтому в большинстве инженерных расчетах при

исследовании движения тел с Землей связывают инерциальную

(неподвижную) систему отсчета.

Учет вращения Земли приобретает значение при больших

относительных скоростях (при расчете движения баллистических ракет) или

для продолжительных по времени движениях (течение рек, воздушные и

морские течения).

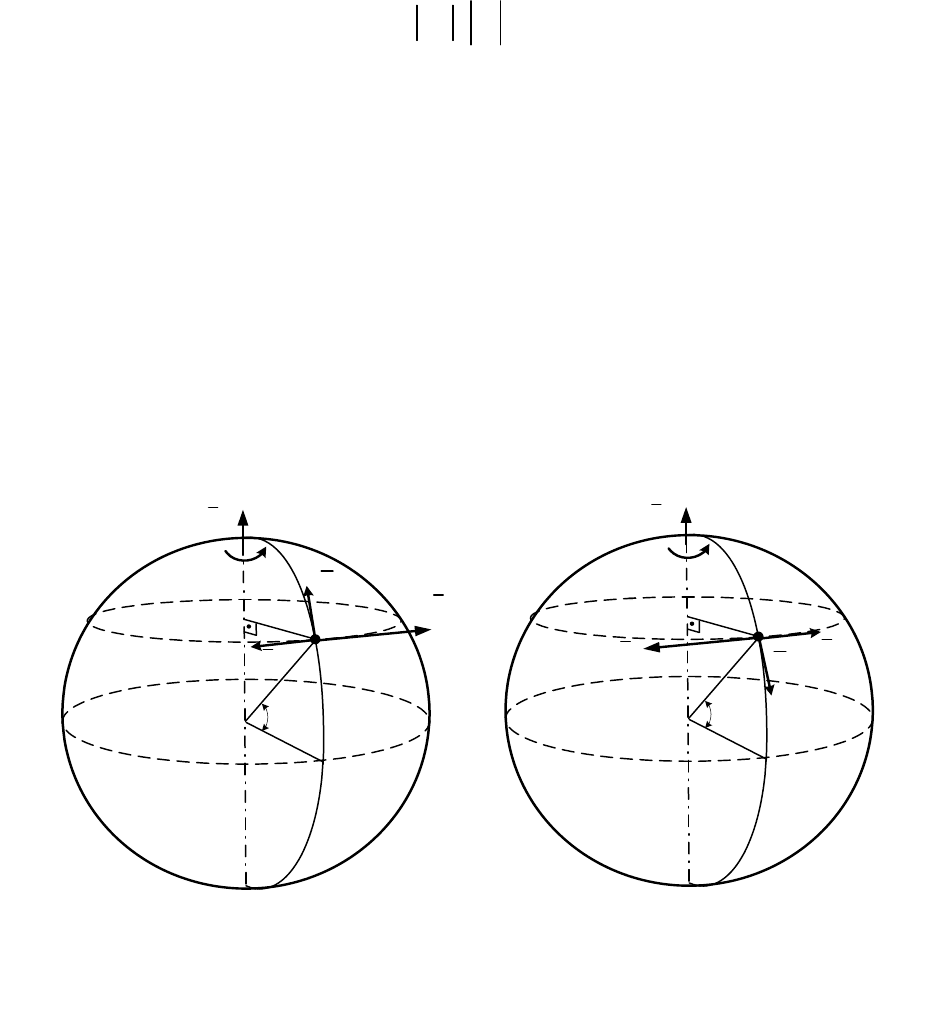
Рассмотрим материальную точку В, равномерно движущуюся

в север-

ном полушарии по меридиану с юга на север (рис. 13.3, а). В этом случае

ускорение Кориолиса

направлено по касательной к параллели на запад,

Тогда кориолисова сила инерции

согласно определению (13.5)

направлена в противоположную сторону, и под действием этой силы точка В

будет отклонятся на восток.

Если же точка В движется в северном полушарии с севера на юг

(рис. 13.3, б), то под действием кориолисовой силы инерции

точка

отклонится на запад.

В обоих случаях в северном полушарии вследствие вращения Земли

тело, движущееся по земной поверхности, будет откланяться вправо от









а б

Рис. 13.3