Валиев Ф.С., Гребенюк Г.И. Сопротивление материалов: основы теории и примеры решения задач (часть 2)

Подождите немного. Документ загружается.

121

значит от размеров и формы подбираемого сечения. В случае

приближенного представления функции

(A )

(например, ап-

проксимации ее в виде алгебраического полинома

br br br

(A ) a bA cA ...ϕ=+++) для подбора сечения достаточно

решить уравнение:

(A )R

=ϕ

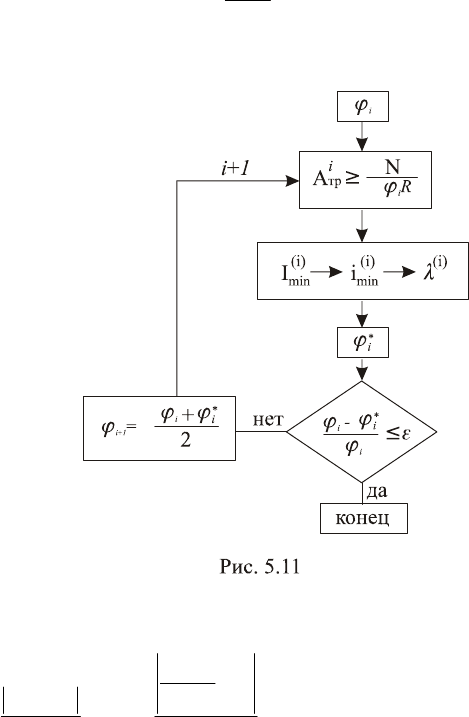
Предпочтительнее, однако, использовании следующего итера-

ционного алгоритма.

Пусть на первой итерации назначено начальное значение

ϕ коэффициента продольного изгиба. Тогда (опуская индекс

«br») из (5.27) найдем требуемую площадь сечения в первом

приближении –

(1)

тр

≥

Учитывая заданную форму сечения, находим размеры, а да-

лее – геометрические характеристики сечения и гибкость вы-

бранного на первой итерации стержня:

(1) (1) (1) (1)

тр min min

AI i→→→λ

С учетом найденного значения гибкости

(1)

определяем по

таблице коэффициентов

- величину действительного коэффи-

циента, для данного материала

. Если

||ϕ−ϕ

≤

<< − на-

перед заданное малое число, например, 0,05), то процесс подбо-

ра сечения заканчивается на первой же итерации. В противном

случае происходит переход к итерации 2. Причем в качестве

ϕ можно принять, например, среднее арифметическое:

ϕ+ϕ

ϕ= Блок – схема описанного алгоритма представлена

на рис 5.11.

Критерий окончания процесса подбора сечения

||ϕ−ϕ

≤ε

предполагает возможность как недогрузки, так и перегрузки.

122

Для исключения перегрузки можно дополнительно поставить

условие

ϕ≥ϕ.

Если ввести в рассмотрение величину расчетного на-

пряжения в сечении

des

вr

σ=

, то условие устойчивости (5.26)

имеет вид:

des

Rσ≤

Поэтому в качестве критерия завершения процесса подбора се-

чения можно использовать условие:

*(i)

des

100% 100% %,

−

σ−

=≤ε (5.29)

где

%ε -заданный допуск в процентах от расчетного сопротив-

ления R.

123

5.7 Пример

выполнения индивидуального задания

по теме: «Расчет сжатого стержня на устойчивость»

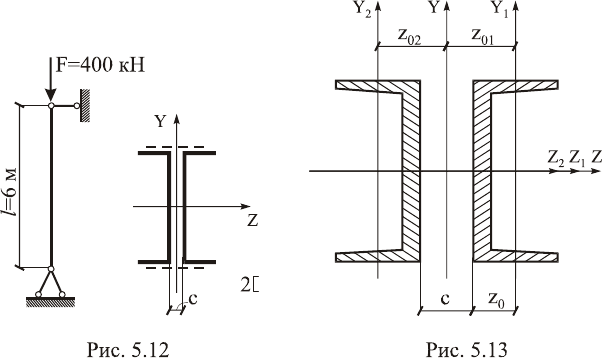
Дано: На рис. 5.12 изображена сжатая стойка. Материал –

сталь 3, состоит из двух прокатных швеллеров по ГОСТ 8240-

89, отстоящих друг от друга на расстоянии “C”. Швеллера со-

единены между собой с помощью планок на сварке. R=200 МПа.

Требуется:

1. С помощью таблицы коэффициентов продольного изгиба ϕ

из условия устойчивости подобрать сечение заданной фор-

мы (определить номера швеллеров) при условии одинаково-

го закрепления стойки в двух главных плоскостях и равно-

устойчивости стержня в этих плоскостях.

Определить размер “C” из условия равноустойчивости стой-

ки в двух главных плоскостях.

Подобранное сечение проверить по условию прочности при

наличии ослабления сечения отверстиями на 15%, т.е. при

= 0,85A

Определить критическое значение силы F и коэффициент

запаса устойчивости к

124

5. Построить график изменения величины критической силы

при изменении длины стойки от 0 до длины, соответствую-

щей гибкости 200.

РЕШЕНИЕ

1. Подбор сечения.

а) Зададим в первом приближении произвольное значение

коэффициента продольного изгиба: пусть ϕ

= 0,5.

Из условия устойчивости (5.28) определим требуемую пло-

щадь поперечного сечения стойки:

(1) 4 2

| N | 400kH

A4010M40

R0,520010ka

−

==⋅=

ϕ⋅⋅Π

см

Для одного швеллера:

(1)

ТР

= 40/2 = 20 см

б) По таблице сортаментов для прокатных швеллеров (ГОСТ

8240-89) находим ближайший по площади швеллер N18 и выпи-

сываем его геометрические характеристики:

= 20,7 см

;

= 1090 cм

;

= 1,94 см;

= 86 см

;

в) Определяем минимальный момент инерции всего сече-

ния. Центральные оси Z и Y являются осями симметрии состав-

ного сечения (рис. 5.13), поэтому они и являются главными цен-

тральными осями сечения.

Запишем формулы для определения моментов инерции со-

ставного сечения с учетом оси симметрии:

zz1011

yy1011

I2(I yA);

I2(I zA).

Здесь z

и y

– расстояния от общих центральных осей Z и

У до центральных осей отдельных фигур (швеллера). Т.к. оси Z

и Z

совпадают, то y

=0, а из рис. 5.13 видно, что

=C/2 + z

Размер “C” – расстояние между швеллерами - неизвестен,

но, согласно условию задачи необходимо его выбрать так, чтобы

обеспечить условие равноустойчивости. Это возможно, если

125

равны главные моменты инерции – I

, т.к. закрепление кон-

цов стойки в обоих плоскостях одинаковое.

Поэтому дальнейший расчет выполняем, используя I

, т.к.

его величина легко находится при y

=0:

zz1

I 2I 2 1090 2180==⋅ = см

г) Определим минимальный радиус инерции сечения.

Т.к. I

, то I

max

min

= I

, значит:

min max z y

2180cм

iiii 7,26см

A220,7см

==== = =

⋅

д) Определяем гибкость –

min

l 1 600см

82,6.

i7,26см

⋅⋅

λ= = =

е) По найденным значениям для стали 3 по табл. 5. 2 нахо-

дим ϕ, используя при этом линейную интерполяцию:

При λ = 80, ϕ = 0,734;

При λ = 90, ϕ = 0,665;

При λ = 82,6:

80 90

(0,734 0,665)

(90) (90 82,6) 0,665 7,4 0,716.

10 10

ϕ−ϕ

−

ϕ=ϕ + − = + ⋅ =

ж) Проверим на устойчивость:

F400кН

134,94 10 кПа R.

A0,716220,710м

−

σ= = = ⋅ <

ϕ⋅⋅⋅

Имеет место значительное недонапряжение, поэтому вы-

полняем расчет во 2-м приближении:

Принимаем новое значение ϕ

0,5 0, 716

0,61.

ϕ+ϕ

ϕ= = =

Дальнейший расчет выполняем по аналогии с расчетом в

первом приближении.

TP 4 2 2

F 400kH

A32,810м 32,8 см

R 0,61 200 10 k a

−

== =⋅ =

ϕ⋅⋅Π

Для одного швеллера: A

тр(1)

= 32,8/2 = 16,4 см

126

По таблице сортаментов находим ближайший по площади

швеллер [ N14 который имеет: А

= 15,6 см

;

= 491 cм

;

= 1,67 см;

= 45,4 см

;

zz1

I 2I 2 491 982см ;==⋅=

br 1

A 2A 2 15,6 31, 2см ;==⋅=

Определим минимальный радиус инерции сечения.

Т.к. I

, то

min max z y

982cм

iiii 5,61см.

A31,2см

==== = =

Определяем гибкость при

l =6 м=600 см.

min

1 600см

107.

i5,61см

μ⋅ ⋅

λ= = =

По найденным значениям для ст.3 по табл. 5.2 находим ϕ,

используя при этом линейную интерполяцию:

При λ = 100, ϕ = 0,599;

При λ = 110, ϕ = 0,537;

При λ = 107:

100 110

(0,599 0,537)

(110) (110 107) 0,537 7,4 0,556.

10 10

ϕ−ϕ

−

ϕ=ϕ + − = + ⋅ =

Проверим устойчивость:

F400кН

230,6 10 кПа R.

A 0,556 31, 2 10 м

−

σ= = = ⋅ >

ϕ⋅⋅

Определим процент перенапряжения:

(230,6 200)

% 100% 100% 15,3% 5%.

R200

−

Δσ = ⋅ = ⋅ = >

Перенапряжение превышает допустимые 5%, поэтому вы-

полняем расчет в третьем приближении.

Принимая во внимание не очень большую величину пере-

напряжения, в 3-м приближении проверим устойчивость сле-

дующего большего номера по табл. сортаментов – [N16.

Из таблицы сортаментов для этого швеллера выписываем:

= 18,1 см

;

127

= 747 cм

;

= 1,80 см;

= 63,3 см

;

zz1

I 2I 2 747 1494см ;==⋅=

br 1

A2A218,136,2см ;==⋅=

Определим минимальный радиус инерции сечения.

Т.к. I

, то

min max z y

1494cм

iiii 6,42см.

A36,2см

==== = =

Определяем гибкость –

min

1600см

93,5.

i6,42см

⋅⋅

λ= = =

По найденным значениям для ст.3 по табл. 5.2 находим

ϕ ,

используя при этом линейную интерполяцию:

При λ = 90, ϕ = 0,665;

При λ = 100, ϕ = 0,599;

При λ = 93,5:

90 100

(0,665 0,599)

(100) (100 93,5) 0,599 6,5 0,642.

10 10

ϕ−ϕ

−

ϕ=ϕ + − = + ⋅ =

Проверим устойчивость:

F400кН

171,6 10 кПа R.

A 0,642 36,2 10 м

−

σ= = = ⋅ <

ϕ⋅⋅

Определим процент недонапряжения:

(171,6 200)

% 100% 100% 14,2%.

R200

−

Δσ = ⋅ = ⋅ = −

Хотя недонапряжение –14,2% и превышает установленные

±5%, следующий меньший номер швеллера N14 не может быть

принят, т.к. он уже был нами рассмотрен во втором приближе-

нии и имел недопустимое перенапряжение – 15,3%.

Окончательно принимаем сечение стойки из двух швелле-

ров N16.

2. Определим необходимое для обеспечения равноустойчи-

вости стойки расстояние между швеллерами “С” (рис. 5.13).

128

Это условие выполняется при I

, т.к. концы стержня в

обоих главных плоскостях закреплены одинаково.

Учитывая, что I

=2I

;

yy1011

I2(I zA),=+

получим:

z1 y1 01 1

2I 2(I z A ).=+⋅ Отсюда имеем:

z1 y1

(747 63,3)cм

z6,15см.

A18,1см

−

== =

Из рис. 5.13 видно, что z

=C/2+z

. Зная значение z

, нахо-

дим:

С = 2z

- 2z

=2·6,15 - 2·1,8 = 8,7 см.

Таким образом, равноустойчивость стойки в двух главных

плоскостях обеспечивается, если расстояние между краями сте-

нок швеллеров будет равно С=8,7 см.

3. Подобранное сечение проверим на прочность при нали-

чии ослабления отверстиями на 15%, т.е. A

= 0,85A

nt br

F F 400кН

130 10 кПа R

A 0,85A 0,85 36,2 10 м

−

== = =⋅ <

⋅⋅

Условие прочности выполняется с большим запасом.

4. Определим критическую силу F

и коэффициент запаса

устойчивости стойки.

Т.к. гибкость для принятого окончательного сечения из

двух швеллеров N16 λ=93,5 < λ

= 100 (для ст.3), критическую

силу определяем по формуле Ф. Ясинского:

= σ

; σ

= a–в·λ.

Эмпирические коэффициенты “

a” и “в” для стали 3 берём

из табл. 5.1

– а = 310 МПа;

в = 1,14 МПа.

= (a–в·λ)·A

= (310–11,14·93,5)·36,2·10

-4

= 0,736 МН =

=736 кН.

Коэффициент запаса устойчивости:

= F

/F = 736кН/400кН = 1,84.

5. Построим график изменения критической силы при из-

менении длины стойки от 0 до длины, соответствующей гиб-

кости 200.

129

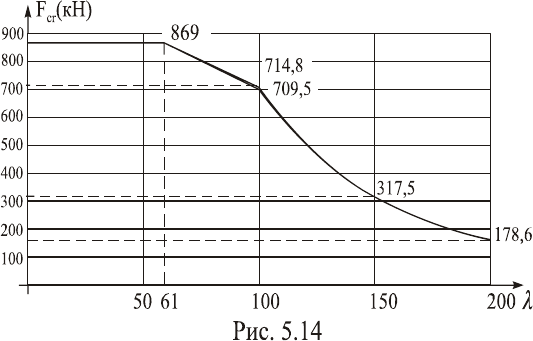
При гибкостях 0 < λ ≤ 61,4 критические напряжения посто-

янны, т.к. они равны пределу текучести стали. Для определения

этого напряжения используем формулу Ф. Ясинского при

61,4λ= :

= 310 – 1,14·61,4 = 240 Мпа = σ

(предел текучести).

= σ

·A

= 240·10

кПа·36,2·10

-4

= 869 кН.

При λ = λ

= 100 (для стали 3) тоже используем формулу Ф.

Ясинского:

= 310 – 1,14·100 = 196 МПа ≈ σ

=200 МПа.

= σ

·A

= 196·10

кПа·36,2·10

-4

= 709,5 кН.

При гибкостях λ ≥ λ

= 100 для определения критических

сил используем формулу Л. Эйлера:

min

(l)

π⋅

Т.к.

min

λ=

то отсюда: μ l = λ·i

min

Тогда при μ=1 получаем:

λ =100, μ

l = 100·6,42см = 642см = 6,42 м.

28 84

210кПа 1494 10 м

F714,8кН.

(6,42м)

−

π⋅ ⋅ ⋅ ⋅

Небольшое расхождение критической силы, определенной

при гибкости 100 по формуле Ф. Ясинского и по формуле Л.

Эйлера объясняется неточностью принятых коэффициентов “

a”

и “в” в формуле Ф. Ясинского.

λ =150; μ

l = 150·6,42см = 963 см = 9,63 м.

28 84

210кПа 1494 10 м

F 317,5кН.

(9,63м)

−

π⋅ ⋅ ⋅ ⋅

λ =200; μ

l = 200·6,42см = 1284см = 12,84 м.

28 84

210кПа 1494 10 м

F178,6кН.

(12, 84м)

−

π⋅ ⋅ ⋅ ⋅

По полученным данным строим график (рис. 5.14).

130

Вопросы для самопроверки

1. В чем заключается явление потери устойчивости сжатого

стержня?

2. Какая сила называется критической силой?

3. Какое дифференциальное уравнение из теории изгиба

лежит в основе вывода формулы Л. Эйлера?

4. Что называется гибкостью стержня? Приведите формулу.

5. Приведите формулу Л. Эйлера для определения критиче-

ской силы?

6. Как учитывается различное закрепление концов стержня

при определении критической силы?

7. Каков предел применимости формулы Л. Эйлера?

8. Как определяется предельная гибкость для формулы Л.

Эйлера?

9. Как определяется критическая сила при напряжениях,

превышающих предел пропорциональности материала?

10. Какой вид имеет график изменения критической силы в

зависимости от гибкости (или длины) для стальных стержней?

11. Приведите формулу Ф. Ясинского

для определения кри-

тической силы и укажите пределы её применимости.