Туманов М.П. Теория импульсных, дискретных и нелинейных САУ
Подождите немного. Документ загружается.

3
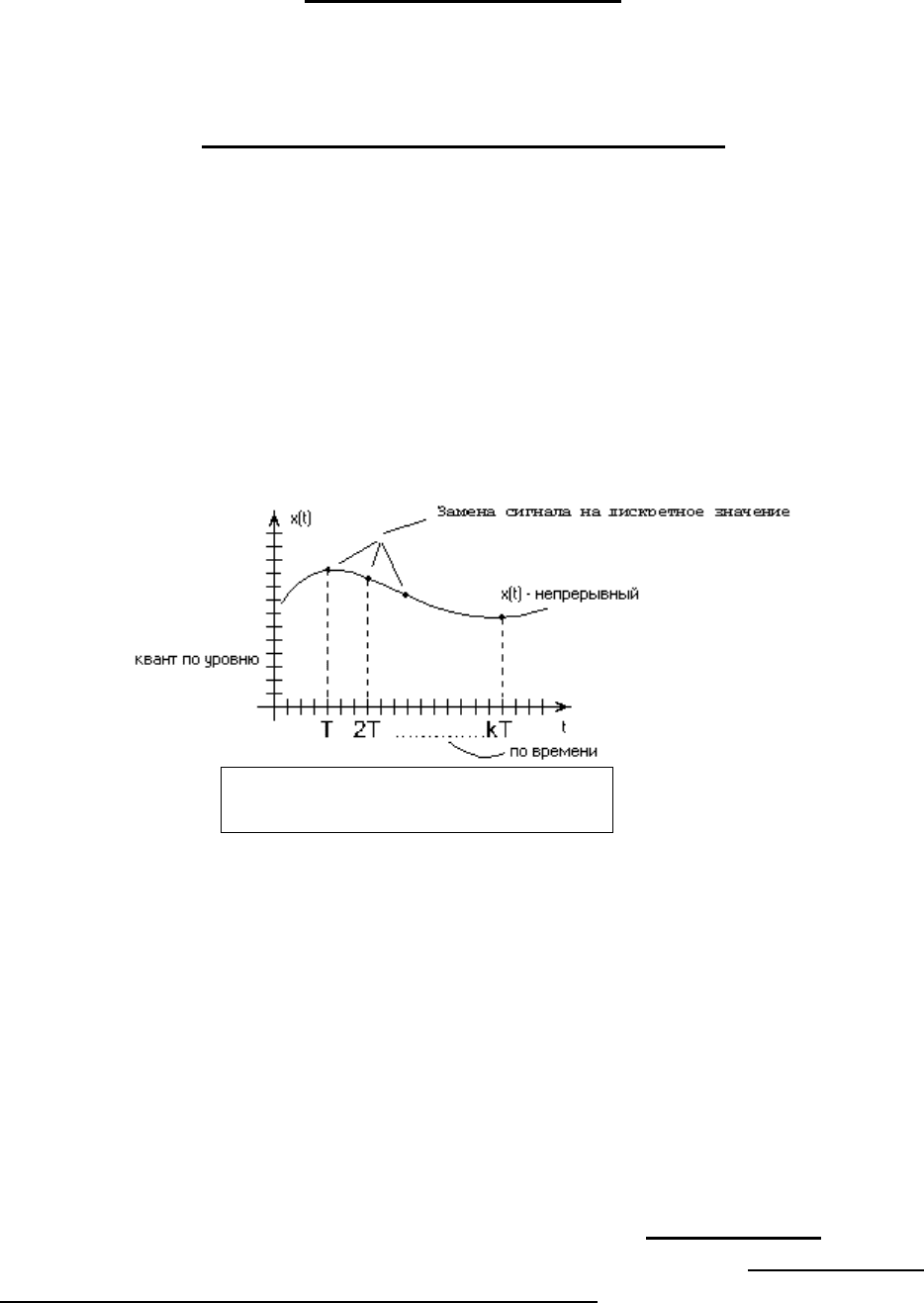
Квантование непрерывного сигнала
по времени и по уровню.
Туманов М.П. Теория импульсных, дискретных и нелинейных САУ:
Учебное пособие. – МГИЭМ. М., 2005, 63 с.
Часть 2 курса "ТАУ"
Теория импульсных, дискретных и нелинейных САУ.
Лекция 1.
Квантование непрерывных сигналов.
Как правило, в системе автоматического управления имеется
квантование сигналов (особенно при цифровых технологиях).
Квантование может быть: по уровню сигнала и по времени.
Как только в состав САУ включается цифровой вычислитель, т.е.
специализированная управляющая ЭВМ, или ЭВМ общего
назначения (ПК со специальными цифро-аналоговыми контрол-
лерами ввода/вывода), или микропроцессорное
устройство
автоматики, немедленно возникают два квантования - по уровню и
по времени.
Рис. 1.1
В результате квантования мы переходим от непрерывного сигнала к
множеству значений в моменты квантования кТ.
(kT)}x
~
{x(t)
квант
⎯⎯→⎯ , где T – шаг квантования по времени,
(kT)x
~
x(kt) ≠
– есть квантованное по уровню значение.
Квантование по времени КПВ и по уровню КПУ сказываются
совершенно по-разному. В частности, если в системе имеется только
квантование по времени – то она остаётся линейной, т.к.
Y(kT)}}{x(kT)}}{βY(kT)αx(kT)
β
α
+
=+
А квантование по уровню - нелинейная операция, поэтому системы, в
которых учитывается эффект квантования по уровню должны
рассматриваться как нелинейные.
Система с квантованием только по времени – импульсная.
Система с квантованием и по времени и по уровню – дискретная.
Основные источники появления таких систем:
4
КПВ – следствие неизбежной дискретности работы ЭВМ.
КПУ – наличие АЦП/ЦАП.

5
Квантование по уровню в АЦП.
Сейчас в промышленных применениях в основном используются 14-
16-разрядные квантователи. Значительно реже 8 и 10- разрядные.
1. Квантование по уровню – это преобразование сигнала с
помощью АЦП/ЦАП, когда диапазон изменения сигнала делится
на ступени в зависимости от разрядности АЦП/ЦАП.
Рис. 1.2
Ступенчатая линия описывает преобразование непрерывной
величины х(t) в квантованную по уровню величину )(
~
kTX .
n
xx
2
minmax
−
=
δ
, где n – разрядность кода
Оценим ошибку квантования при 8- и 16-разрядном АЦП/ЦАП:
при 8-разрядном кодировании:
)(104,0
minmax
2
8
xx −⋅≈
−
δ
при 16-разрядном кодировании:
)(1015,0
minmax
4
16
xx −⋅≈
−
δ
Важен также вопрос, связанный с представлением полученного кода.
Для эффективности использования 16-разрядного кода надо
использовать минимум 16-разрядную машину.
Для использования 20-разрядного кода надо использовать либо 32-
разрядную машину, либо считывать за 2 такта 16-разрядные данные.
⇒ Разрядность микропроцессорного контроллера, быстродействие и
погрешность преобразования связаны. Необходимо тщательно
выбирать платформу реализации контроллера и увязывать её с
выбираемыми типами цифровых преобразователей.
Видно, что погрешность при 16-разрядном кодировании достаточно
низка, по крайней мере, обычно существенно ниже погрешности
других элементов системы, например, датчиков.
Напрашивается вывод, что погрешностью 16 и более разрядного
АЦП/
ЦАП можно пренебречь, однако, это не всегда верно!
Покажем, что и при достаточно малой погрешности АЦП/ЦАП ошибка
может с течением времени накапливаться. Для примера рассмотрим
некоторый блок, в котором обрабатывается сигнал с ПФ W(p).

6
Рис.1.4
∫
−=
t
th
0
)(y(t)
τ
u
τ
τ
)d(
,
h(t) – весовая функция, соответствующая W(p).
Пусть в результате АЦ преобразования, а также ошибок арифметики
вычисления получаем:
),()()(
),()()(
),()(y(t)
0
0
0
tututu
yhthth
tyty
Δ+=
Δ+=
Δ+=
где
000
,, uhy – истинные значения сигналов,
uh ΔΔ ,
– ошибки квантования по уровню, причем
h
th
δτ
<−Δ )(
не зависят от времени (оценки погрешности);
u
tu
δ
<Δ )(
yΔ
– ошибка вычисления сигнала, тогда
∫∫∫∫∫
ΔΔ+Δ+Δ+=Δ+Δ+=
ttttt
tdhduhduhduhduuhhty
0
0
000
0
0
0000
))(()(
τττττ
,
где
)(
0
0
00
tyduh
t
=
∫
τ
.
∫∫
Δ+Δ=Δ
tt
dhuduhty
0
0
0
0
)(
ττ
Чтобы оценить абсолютное значение погрешности можно учесть
оценки
0
h
и
0
u :
h
Mh ≤
0
u
Mu ≤
0
tMtMy
uhhu
⋅+⋅≤Δ
δδ
Очевидно далее, что в простейшем случае, когда h
0
=const, ∆u=const,
∆h=const
и u
0
=const, накопленная погрешность может неограниченно
возрастать с течением времени. На самом деле, погрешность
частично компенсируется, т.к. меняется ее знак.
Замечание 1.
Повышение разрядности АЦП/ЦАП позволяет добиться
требуемой точности, если не происходит недопустимого накопления
погрешности.
Замечание 2
. Заметим, что в замкнутой САУ накопление
погрешностей обычно бывает гораздо меньше, так как работает
принцип ОС, для которого погрешность квантования - просто помеха.
Можно пренебречь,
так как имеет 2
порядок малости
7
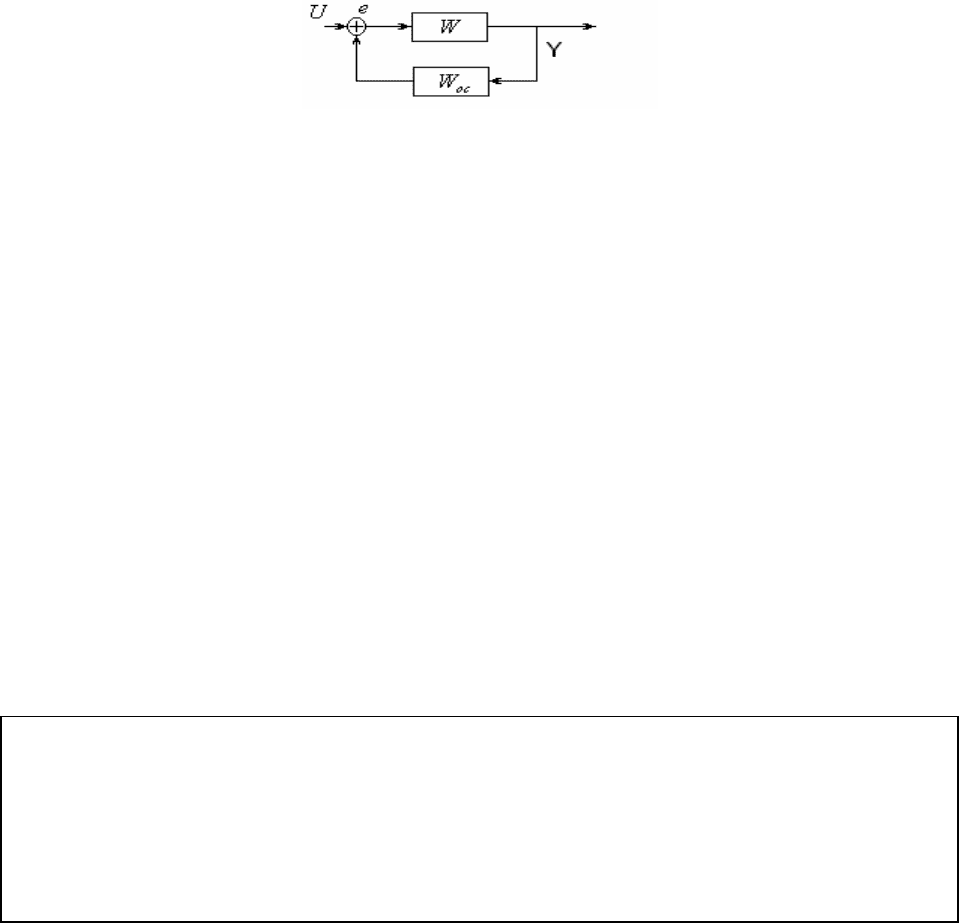
Рис. 1.5 Компенсация погрешности в замкнутой системе.
В самом деле, в соответствии с принципом управления по
отклонению, с помощью обратной связи происходит уменьшение
любых отклонений выходной величины Y от задающего воздействия,
вне зависимости от причины их возникновения (в том числе, из-за
ошибок квантования по уровню).
2. Квантование по времени
возникает в системе из-за того, что ввод
и вывод информации в ЭВМ происходит с некоторой периодичностью
и не чаще. Пусть T – период квантования по времени.
При правильном проектирование САУ (с достаточной разрядностью по
АЦП/ЦАП) КПУ чаще всего можно пренебречь, если учесть
накопление погрешности, а КПВ необходимо учитывать.
Как правило, не
удается сделать скорость ввод/вывод информации до
такой степени высокой, чтобы полностью пренебречь квантованием по
времени. Поэтому важно иметь теорию расчёта САУ с учётом КПВ.
Системы, в которых имеется только квантование по времени (КПВ), а
квантованием по уровню (КПУ) можно пренебречь, называются
импульсными в отличие от дискретных систем.
Дискретные системы
– нелинейные, их изучение представляет слож-
ную задачу, ее лучше избегать, повышая разрядность квантования.
Для импульсных систем имеется удобный математический аппарат.
8
∑
∑
∞
=
∞
=
−−−−=
−−−−=
0
*
0
))(1)(1)()(
))(1)(1()(
k
k
STktTkttftf
STktTkttp
Импульсные системы.
Описание процесса квантования по времени. Реальный и
идеальный квантователи.
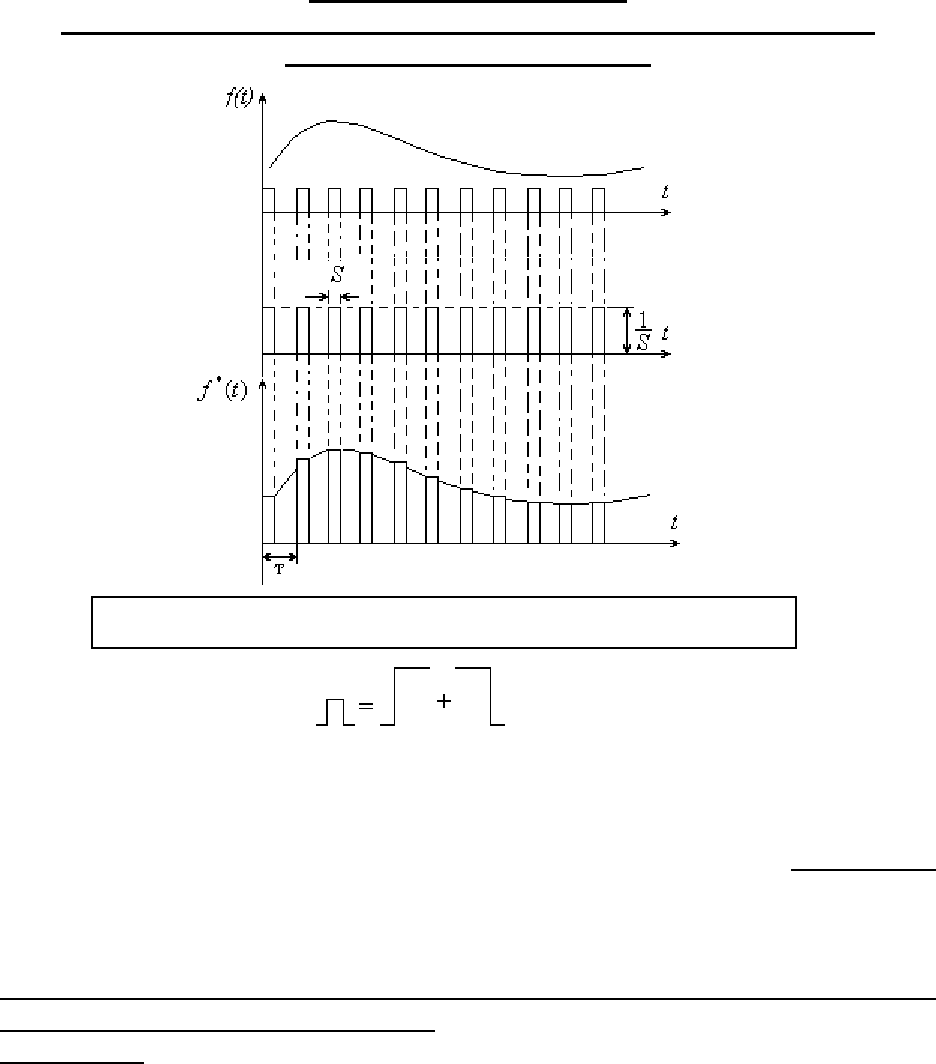
Рис. 1.6
Рассмотрим процесс квантования по
времени, как результат умножения
исходной непрерывной функции на
специальную импульсную последова-
тельность р(t) очень узких импульсов.
Фактически мы рассматриваем квантование, как импульсную
амплитудную модуляцию - АИМ.
Замечание
: если просто уменьшать ширину импульса, то в пределе
энергия импульсов f
*
(t) будет уменьшаться, стремясь к 0.
Чтобы не потерять энергию импульса дополнительно умножаем
результат на 1/s.
Обратим внимание на вершину импульса, она должна повторть форму
функции, именно тогда такое квантование – линейная операция.
При очень узком импульсе вершину можно взять плоской, как показано
на рисунке, чем уже иимпульс, тем меньше ошибка при использовании
импульсов с плоской вершиной.
Квантование как умножение на импульсную последовательность
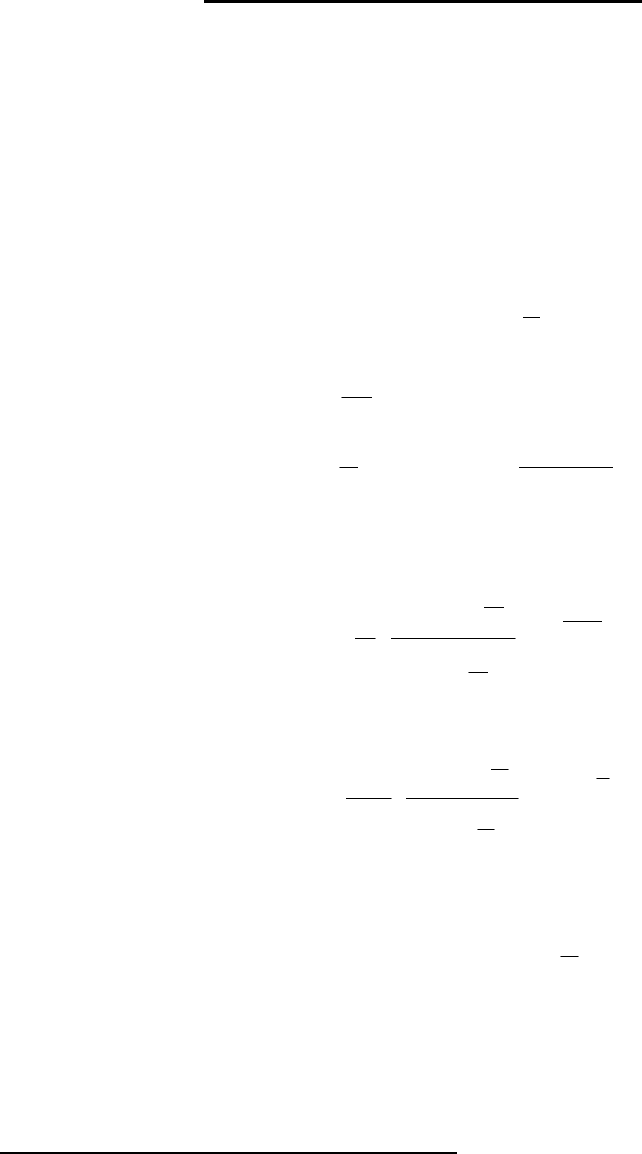
9
S
eCtp
tjk
k
k
p
1
)( ⋅=
∑
∞
−∞=
ω
•
Лекция 2. Спектр квантованного сигнала.
Вершина импульсов считается плоской, а сами импульсы
достаточно узкими, в противном случае учет неплоской вершины
импульса приводит к большим сложностям, хотя такой учёт
возможен.
Вычислим теперь спектр квантованного сигнала, т.е. выясним, что
происходит со спектром при квантовании.
Для этого вначале разложим p(t) в ряд Фурье:
(*)
∫
−
−
−
==
=
T
p
Sik
tjk
k
p
Tjk
e
dtetp
T
C
T
p
p
0
1
)(
1
2
ω
π
ω
ω
ω
Выразив экспоненту по формуле Эйлера и через половинные углы,
получаем такую формулу:
2
2
)
2
sin(
Sk
j
p
p
k
p
e
S
k
S
k
T
S
C
ω
ω
ω
−
⋅⋅=
Подставим последнее выражение в (*) и получим:
tjk
S
jk
p
p
k
pp
e
S
k
S
k
ST
S
tp
ωω
ω
ω
+−
∞
−∞=
⋅⋅
⋅
=
∑
2
2
)
2
sin(
)(
(S/T – скважность импульсов р(t))
S
etfCtf
tjk
k
k
p
1
)()(
*
⋅=
∑
∞
−∞=
ω
Теперь можно найти спектр квантованного сигнала.
Спектр
)(
*
tf : ))(()(
**
tfjF Φ=
ω
(преобразование Фурье)
Теорема о преобразовании Фурье:
)())((
p
tjk
jkjFetx
p
ωω
ω
−=⋅Φ ,
Эта простая теорема называется ещё теоремой о сдвиге
изображения в частотной области. Она показывает, что умножение
оригинала на мнимую экспоненту приводит к сдвигу

10
n
S
k
S
kC
p
pk
⋅=⋅
=⋅=
πω
ω
2
0)
2
sin(;0
преобразования Фурье в комплексной области на этот же самый
показатель. В силу этой теоремы можем записать:
∑
∞
−∞=
⋅−=
k
pk
S
jkjFCjF
1
)()(
*
ωωω
(**)
Таким образом, вместо исходного спектра непрерывного сигнала
получается спектр квантованного сигнала, состоящий из
бесконечного числа компонентов. Рассмотрим характерные случаи.
Пусть исходный сигнал f(t) есть гармонический с частотой
0
ω
:
ttf
0
sin)(
ω
=
Рис. 2.1
Некоторые коэффициенты С
к
могут быть обращены в ноль выбором
скважности импульсов квантования.
т.е. при некоторых соотношениях между частотой квантования и
шириной импульсов квантования соответствующая гармоника
может отсутствовать. Этим часто пользуются, если к спектру
квантованного сигнала предъявляются дополнительные
требования.
Пусть теперь исходный сигнал имеет конечную ширину
спектра (0 - ω
c
), или, в терминах обычной частоты:
f
max
< ω
c
/ 2π . (2.1)
Такой спектр должен встречаться чаще всего, и обычно известно,
какова ширина спектра полезного сигнала. Однако, реально, спектр
всё-таки не бывает жёстко ограниченным. Этому может мешать,
например, наличие помех (шумов), в том числе, и от квантования.
Линейчатый спектр
11
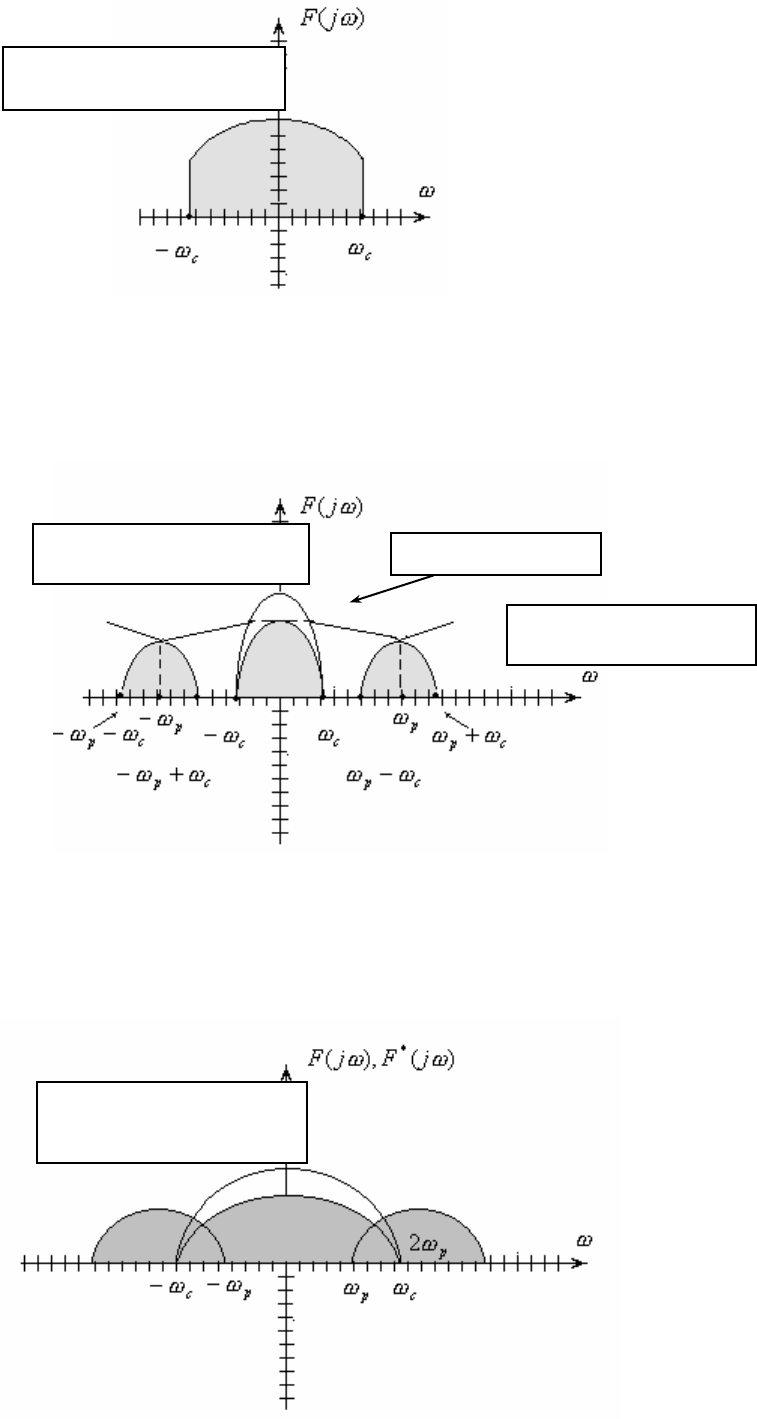
Рис. 2.2
Возможны два случая:
1. ω
р
> 2ω
c
частота квантования больше максимальной ширины спектра сигнала.
Рис. 2.3
Очевидно, что в этом случае отдельные составляющие спектра
квантованного сигнала не пересекаются и явно отделены.
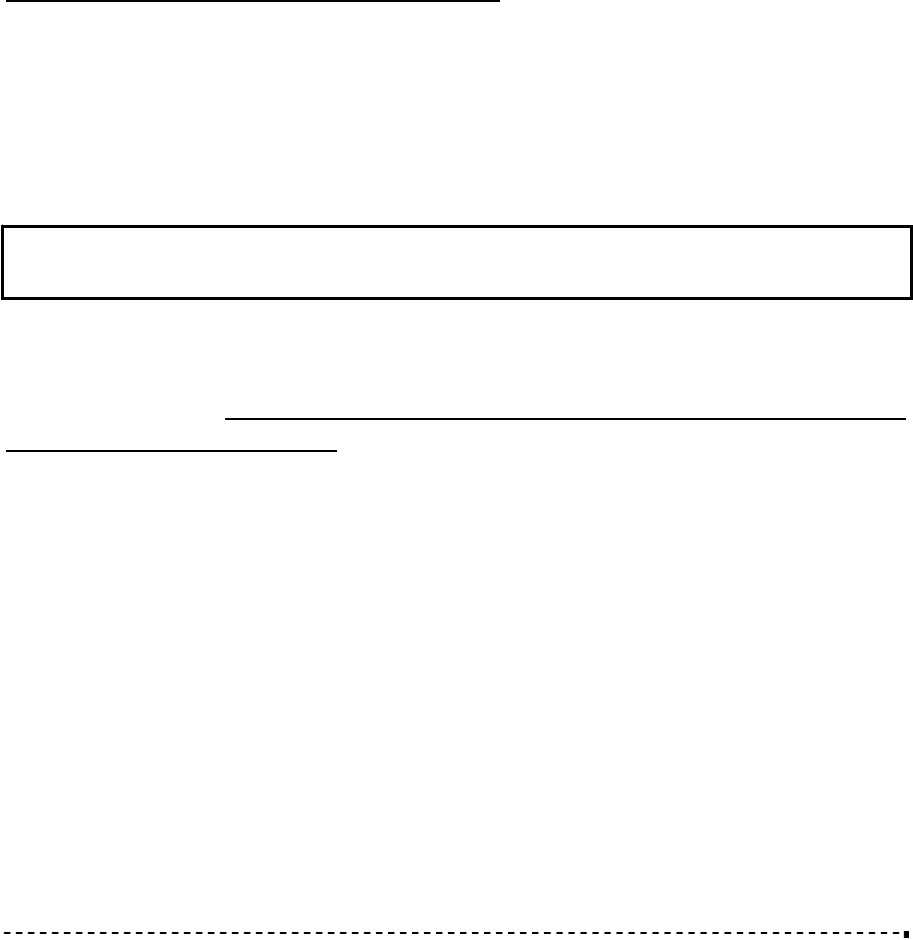
2. ω
р
< 2ω
c
частота квантования меньше максимальной ширины спектра сигнал.
Рис. 2.4
Ограниченный спектр
исходного сигнала
Бесконечный спектр
квантованного сигнала
Компоненты спектра
не пе
р
ек
р
ываются
Компоненты спектра
квантованного сигнала
п
ере
к
р
ыв
аю
т
с
я
Исходный спектр
12
Очевидно, что в этом случае отдельные составляющие спектра
квантованного сигнала пересекаются и не отделены друг от друга.
Несмотря на то, что после квантования полезный сигнал
рассматривается лишь в полосе частотой (-ω
c
… ω
c
), именно в
этой полосе частот появляются дополнительные составляющие,
которые к тому же сдвинуты на величину никак не связанную с
гармониками исходного сигнала, а зависящую от разности
частотой квантования и частоты соответствующей
гармоники.
Для того чтобы заведомо можно было бы восстановить исходный
сигнал из квантованного должно выполняться условие (1), которое
называется
теоремой Котельникова-Шеннона или импульсной
теоремой. Иногда также эта теорема называется теоремой
отсчётов.
Теорема Котельникова - Шеннона:
При выполнении условия (1), что возможно в условиях
ограниченного спектра сигнала и достаточно высокой частоты
квантования ω
р
> 2ω
c
(Т < 1/(2f
max
), потери информации не
происходит и она может быть полностью восстановлена.
То есть из квантованного сигнала можно без потерь восстановить
исходный непрерывный сигнал.
Эта важнейшая теорема является теоретической основой всей
цифровой обработки, хранения и передачи сигналов.
Заметим также что невыполнение условия Котельникова (1) ещё не
означает, что восстановление исходного сигнала заведомо
невозможно! Теорема Котельникова - Шеннона не является
необходимым условием. Например, если форма исходного сигнала
заранее известна, то он обычно может быть восстановлен и из
сложного спектра квантованного сигнала при невыполнении (1). Но
это будет уже , скорее, задача обнаружения известного сигнала, а
не восстановление абсолютно неизвестного сигнала с конечной
шириной спектра.
Снова отметим, что практически не бывает сигналов с конечной
шириной
спектра. Инженерное решение, применяемое в цифровой
обработке сигналов, заключается в том, что ещё до квантования
сигнала нужно ограничить полосу сигнала необходимой шириной,
применяя фильтр предварительной обработки. Следует иметь
ввиду, что такая фильтрация гораздо эффективнее
фильтрации после квантования.
