Tsoulfanidis N. Measurement and detection of radiation
Подождите немного. Документ загружается.

38
MEASUREMENT
AND
DETECTION OF RADIATION
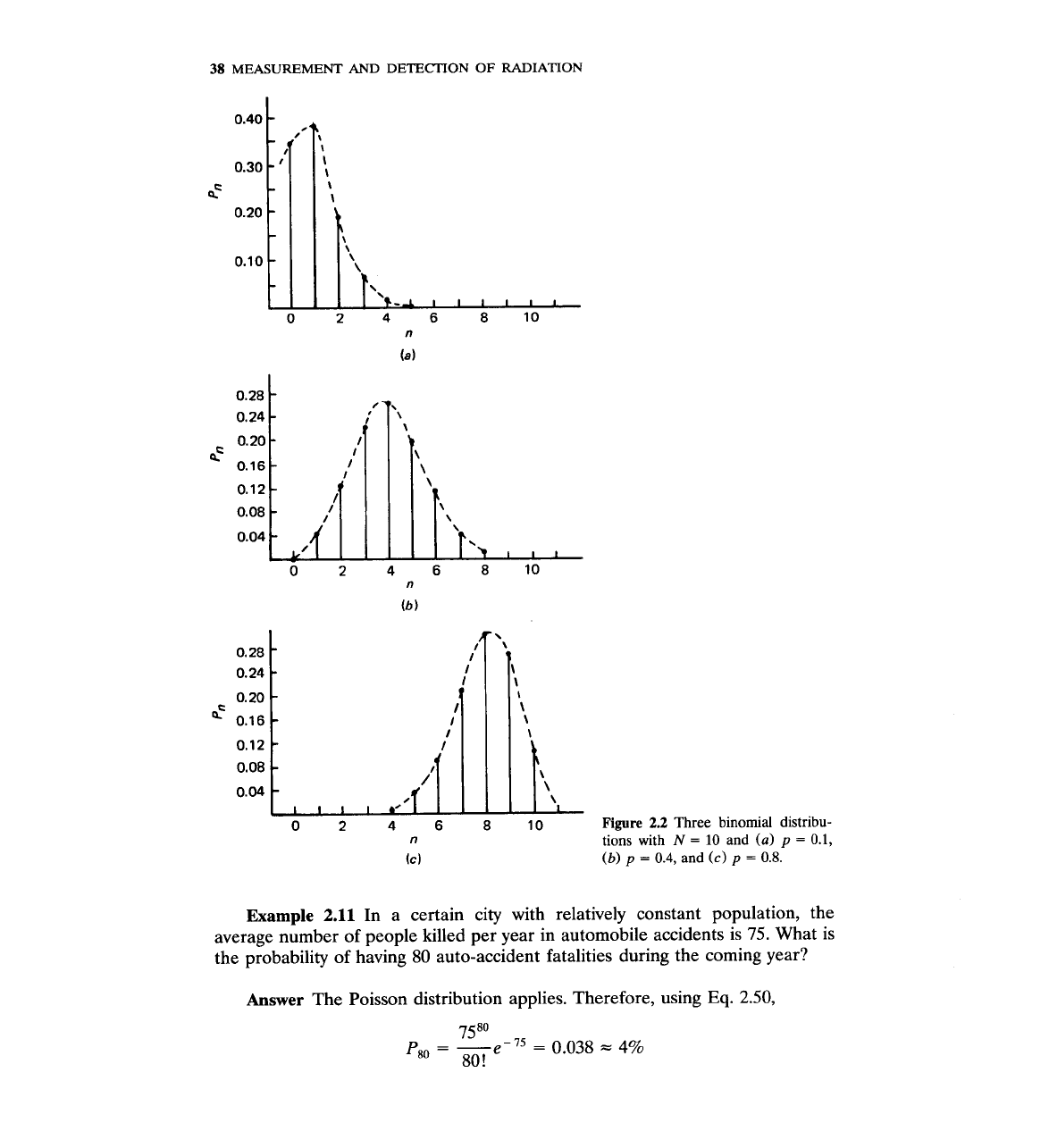
Figure
2.2
Three binomial distribu-
tions with
N
=
10
and
(a)
p
=
0.1,
(b)
p
=
0.4,
and
(c)
p
=
0.8.
Example
2.11
In a certain city with relatively constant population, the
average number of people killed per year
in
automobile accidents is
75.
What is
the probability of having
80
auto-accident fatalities during the coming year?
Answer
The Poisson distribution applies. Therefore, using
Eq.
2.50,
75,O
P,,
=
-
e-75
=
0.038
-
4%
80!

STATISTICAL
ERRORS
OF
RADIATION COUNTING
39
The Poisson distribution satisfies
The mean m is equal to
m
-
m=n=
C
nPn
=
m
n
=
0
The variance is
The standard deviation
a
is
Figure
2.3
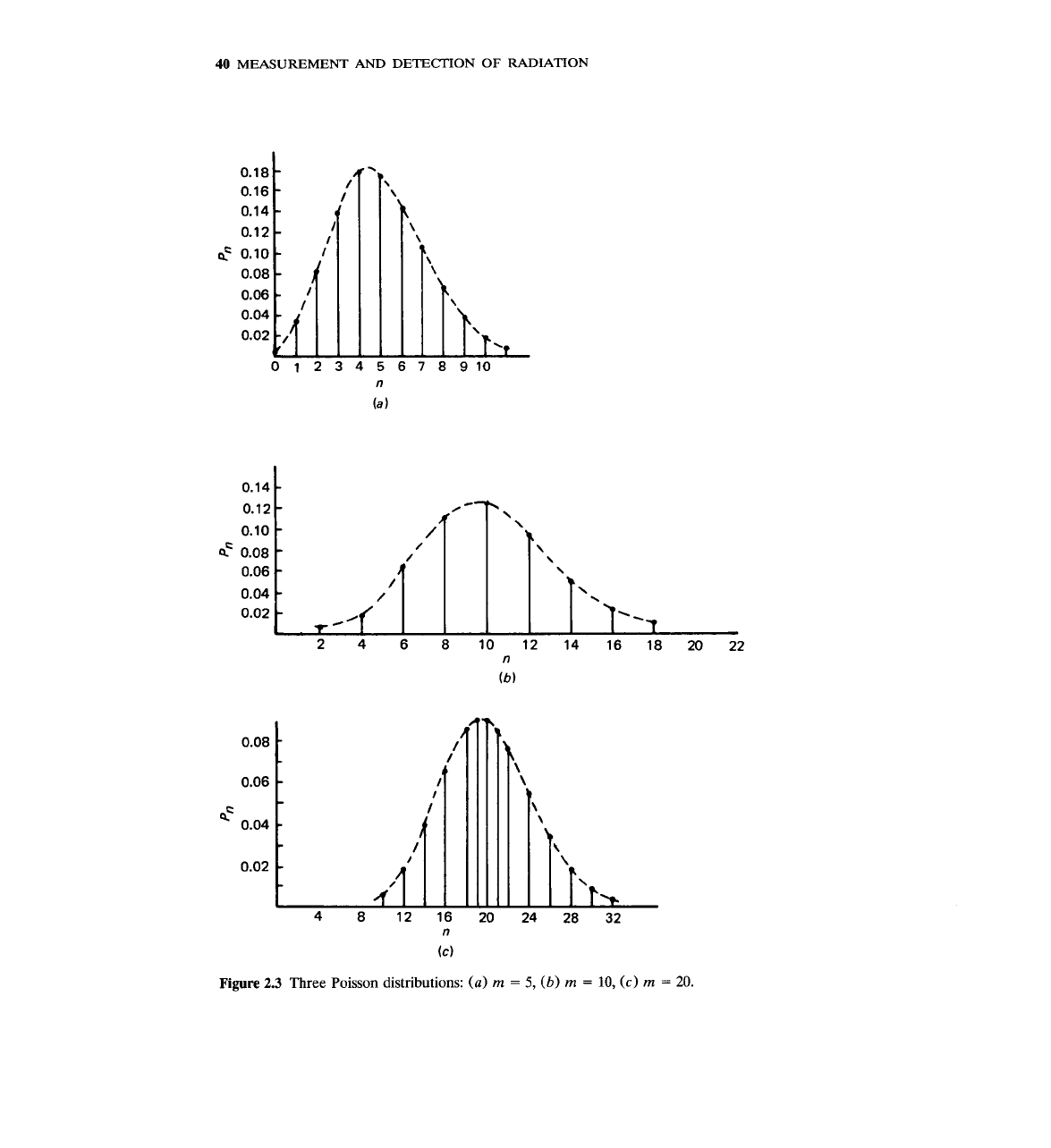
shows the Poisson distribution for three different means. It should be
pointed out that as the mean increases, the Poisson distribution becomes
symmetric around the mean. For m
=
20, the distribution is already for all
practical purposes symmetric around the mean, and it resembles the normal
distribution, which is discussed next.
2.10
THE NORMAL (GAUSSIAN) DISTRIBUTION
Both the binomial and Poisson distributions apply to discrete variables, whereas
most of the random variables involved in experiments are continuous. In
addition, the use of discrete distributions necessitates the use of long or infinite
series for the calculation of such parameters as the mean and the standard
deviation (see Eqs. 2.47, 2.48, 2.52, 2.53). It would be desirable, therefore, to
have a pdf that applies to continuous variables. Such a distribution is the normal
or Gaussian distribution.
The normal distribution
G(x)
is given by
where G(x)
dx
=
probability that the value of
x
lies between
x
and
x
+
&
m
=
average of the distribution
a
'
=
variance of the distribution
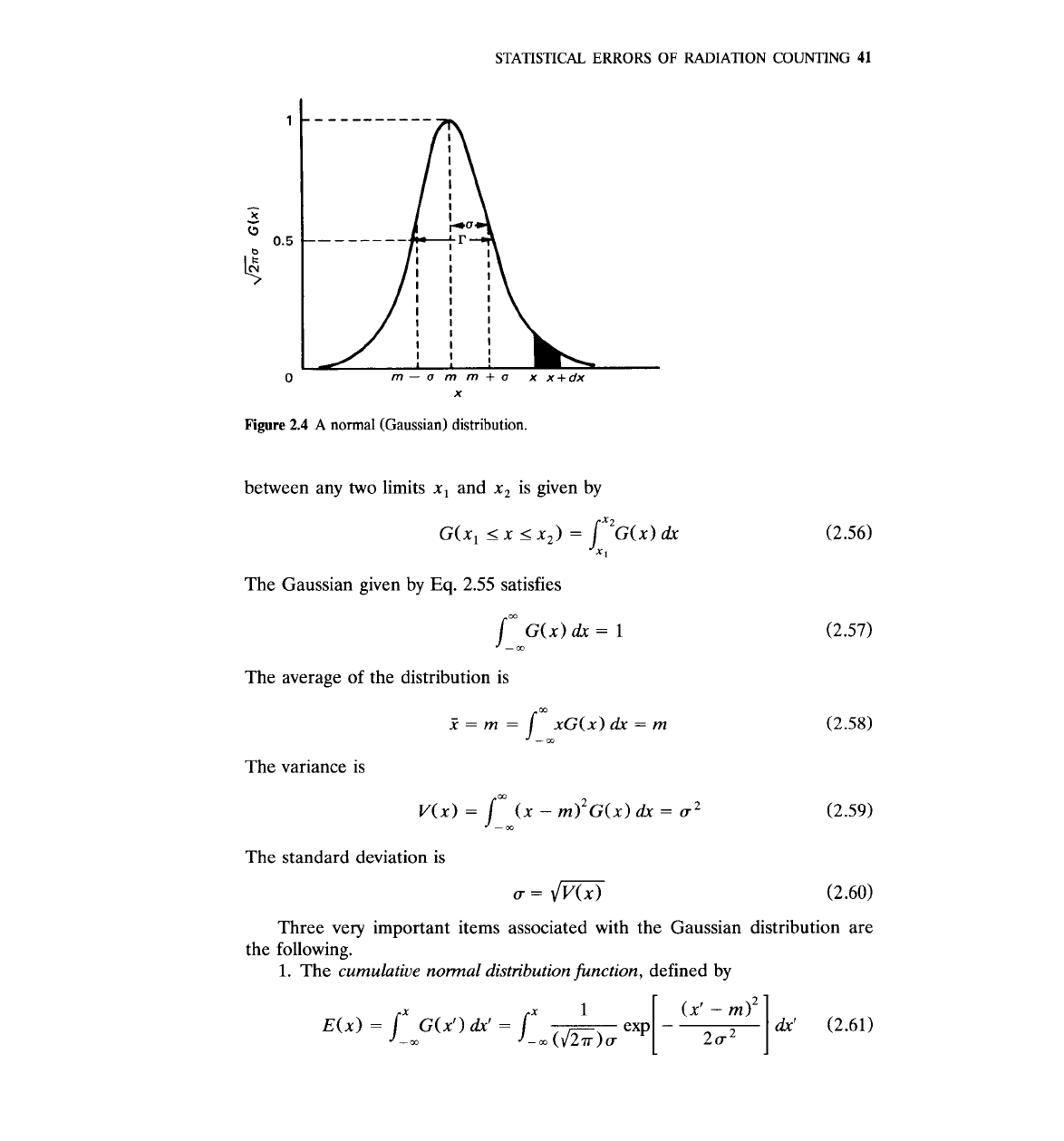
Notice that this distribution, shown in Fig. 2.4, has a maximum at
x
=
m,
is
symmetric around m, is defined uniquely by the two parameters
u
and m, and
extends from
x
=
-m
to
x
=
+m.
Equation 2.55 represents the shaded area
under the curve of Fig. 2.4. In general, the probability of finding the value of
x
40
MEASUREMENT
AND
DETECTION OF RADIATION
Figure
23
Three
Poisson distributions:
(a)
rn
=
5,
(b)
rn
=
10,
(c)
rn
=
20.
STATISTICAL ERRORS OF RADIATION COUNTING
41
0
m-o
m
m+o
x
x+dx
X
Figure
2.4
A
normal (Gaussian) distribution.
between any two limits
x,
and
x2
is given by
The
The
Gaussian given by
Eq.
2.55
satisfies
average of the distribution is
The variance is
The standard deviation is
Three very important items associated with the Gaussian distribution are
the following.
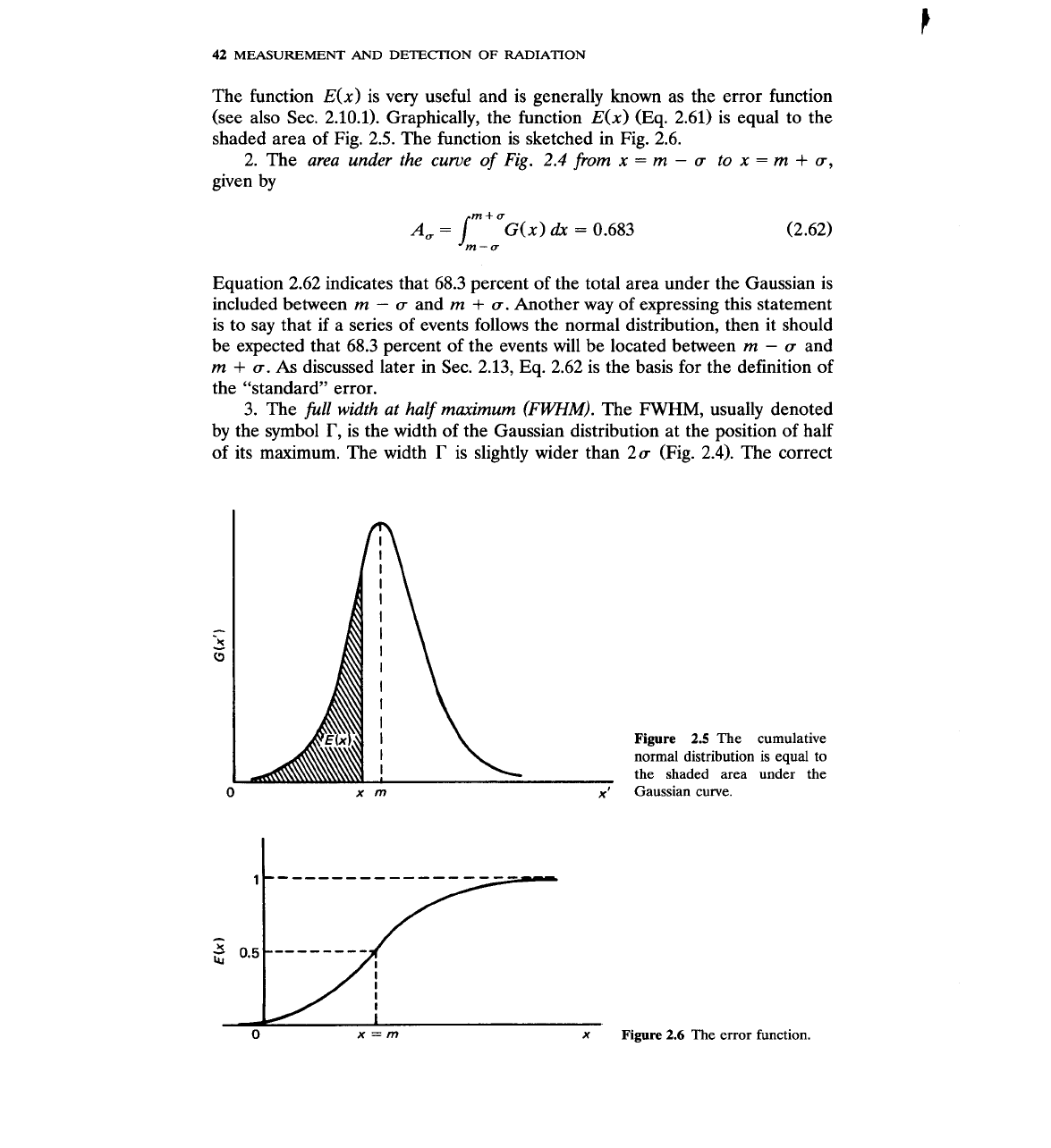
1.
The
cumulative normal distribution function,
defined by
x
1 (x'
-
m)
E(x)
=
G(xt)
dx'
=
-m
EX^[-
2u2
]
&'
(2.61)
42
MEASUREMENT AND DETECTION OF RADIATION
The function E(x) is very useful and is generally known as the error function
(see also Sec. 2.10.1). Graphically, the function E(x) (Eq. 2.61) is equal to the
shaded area of Fig. 2.5. The function is sketched in Fig. 2.6.
2. The
area under the curve of
Fig.
2.4
from
x
=
m
-
u
to
x
=
m
+
u,
given by
Equation 2.62 indicates that 68.3 percent of the total area under the Gaussian is
included between
m
-
u and
m
+
u. Another way of expressing this statement
is to say that if a series of events follows the normal distribution, then it should
be expected that 68.3 percent of the events will be located between
m
-
u and
m
+
a.
As
discussed later in Sec. 2.13, Eq. 2.62 is the basis for the definition of
the "standard" error.
3. The
full
width at half maximum
(FWHM).
The
FWHM,
usually denoted
by the symbol r, is the width of the Gaussian distribution at the position of half
of its maximum.
The
width
r
is slightly wider than 2u (Fig. 2.4). The correct
Figure
2.5
The
cumulative
normal distribution is equal to
the shaded area under the
0
x
m
x'
Gaussian curve.

STATISTICAL ERRORS OF RADIATION COUNTING
43
relationship between the two is obtained from Eq. 2.55 by writing
Solving this equation for
r
gives
The width
r
is an extremely important parameter in measurements of the
energy distribution of particles.
2.10.1
The
Standard Normal Distribution
The evaluation of integrals involving the Gaussian distribution, such as those of
Eqs. 2.56, 2.61, and 2.62, requires tedious numerical integration. The result of
such integrations is a function of
m
and
u.
Therefore, the calculation should be
repeated every time
m
or
u
changes. To avoid this repetition, the normal
distribution is rewritten in such as way that
m=O
and
u=1
The resulting function is called the
standard normal distribution.
Integrals
involving the Gaussian distribution, such as that of Eq. 2.61, have been tabu-
lated based on the standard normal distribution for a wide range of
x
values.
With the help of a simple transformation, it is very easy to obtain the integrals
for any value of
m
and
u.
The standard normal distribution is obtained by defining the new variable.
x-m
t=-
u
Substituting into Eq. 2.55, one obtains
It is very easy to show that the Gaussian given by Eq. 2.65 has mean
and variance
The cumulative standard normal distribution function, Eq. 2.61, is now written
as

44
MEASUREMENT AND DETECITON OF RADIATION
or, in terms of the error function that is tabulated
where
Example
2.12
The uranium fuel of light-water reactors is enclosed in
metallic tubes with an average outside diameter (OD) equal to 20 mm. It is
assumed that the OD is normally distributed around this average with a
standard deviation
a
=
0.5 mm. For safety reasons, no tube should be used with
OD
>
21.5 mm or OD
<
18.5 mm.
If
10,000 tubes are manufactured, how many
of them are expected to be discarded because they do not satisfy the require-
ments given above?
Answer
The probability that the
OD
of a tube is going to be less than
18.5
mm or greater than 21.5 mm is
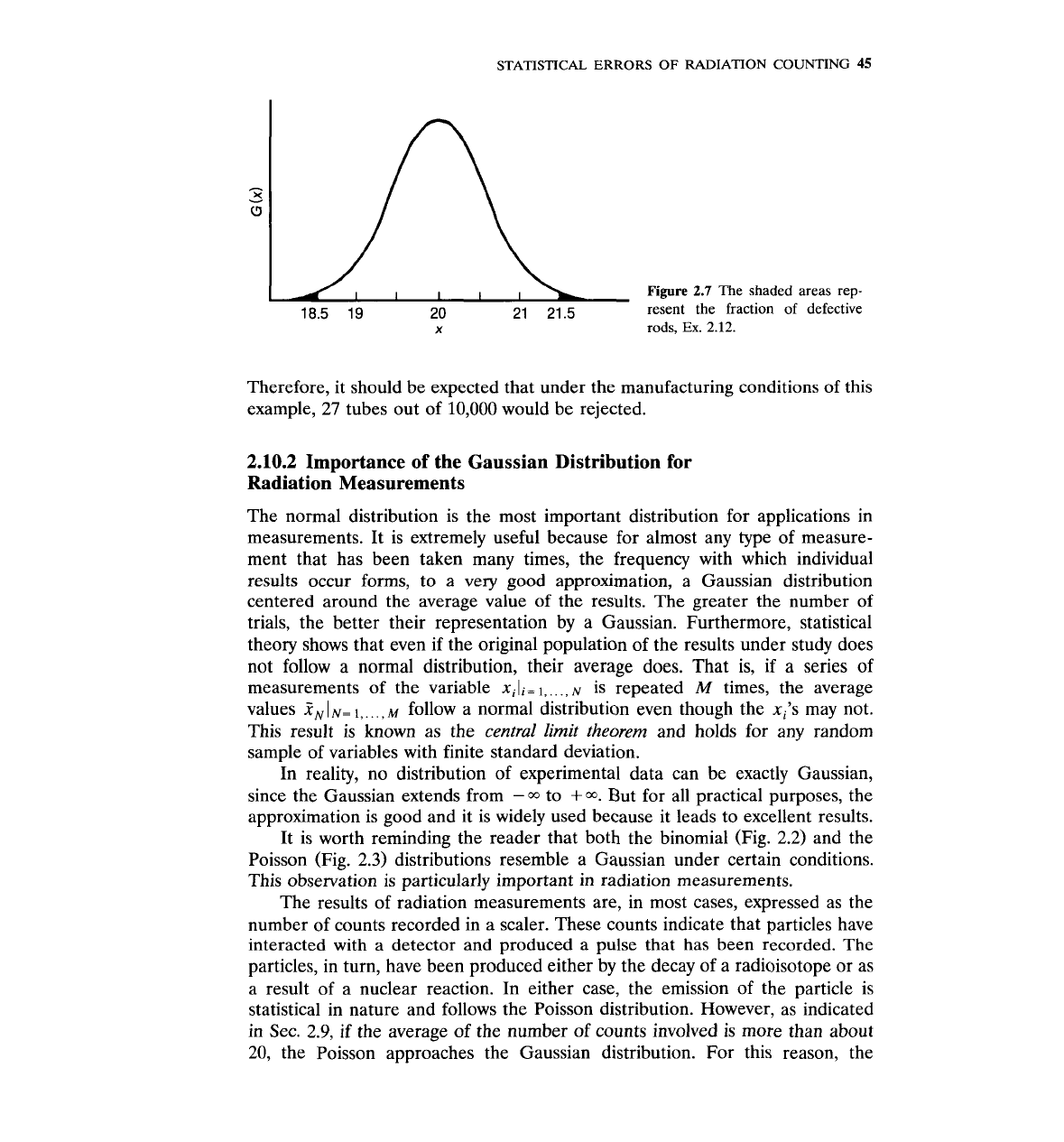
Graphically, the sum of these two probabilities is equal to the two shaded areas
shown in Fig. 2.7.
In terms of the standard normal distribution and also because the two
integrals are equal, one obtains
where
x
-
20
t
=
---
0.5
This last integral is tabulated in many books, handbooks, and mathematical
tables (see bibliography of this chapter). From such tables, one obtains
which gives
G(x
<
18.5)
+
G(x
>
21.5)
=
0.0027
STATISTICAL
ERRORS
OF
RADIATION COUNTING
45
Figure
2.7
The shaded areas rep-
resent the fraction of defective
rods,
Ex.
2.12.
Therefore, it should be expected that under the manufacturing conditions of this
example, 27 tubes out of 10,000 would be rejected.
2.10.2
Importance of the Gaussian Distribution for
Radiation Measurements
The normal distribution is the most important distribution for applications in
measurements. It is extremely useful because for almost any type of measure-
ment that has been taken many times, the frequency with which individual
results occur forms, to
a
very good approximation, a Gaussian distribution
centered around the average value of the results. The greater the number of
trials, the better their representation by a Gaussian. Furthermore, statistical
theory shows that even if the original population of the results under study does
not follow a normal distribution, their average does. That is, if a series of
measurements of the variable
xili=
I,...,
N
is repeated
M
times, the average
values
ZN
I
N=
.
.
,
follow a normal distribution even though the xi's may not.
This result is known as the
central limit theorem
and holds for any random
sample of variables with finite standard deviation.
In reality, no distribution of experimental data can be exactly Gaussian,
since the Gaussian extends from
-
w
to
+m.
But for all practical purposes, the
approximation is good and it is widely used because it leads to excellent results.
It is worth reminding the reader that both the binomial (Fig. 2.2) and the
Poisson (Fig. 2.3) distributions resemble a Gaussian under certain conditions.
This observation is particularly important in radiation measurements.
The results of radiation measurements are, in most cases, expressed as the
number of counts recorded in a scaler. These counts indicate that particles have
interacted with a detector and produced a pulse that has been recorded. The
particles, in turn, have been produced either by the decay of a radioisotope or as
a result of a nuclear reaction. In either case, the emission of the particle is
statistical in nature and follows the Poisson distribution. However, as indicated
in
Sec. 2.9, if the average of the number of counts involved is more than about
20, the Poisson approaches the Gaussian distribution. For this reason, the

46
MEASUREMENT
AND
DETECTION OF RADIATION
individual results of such radiation measurements are treated as members of a
normal distribution.
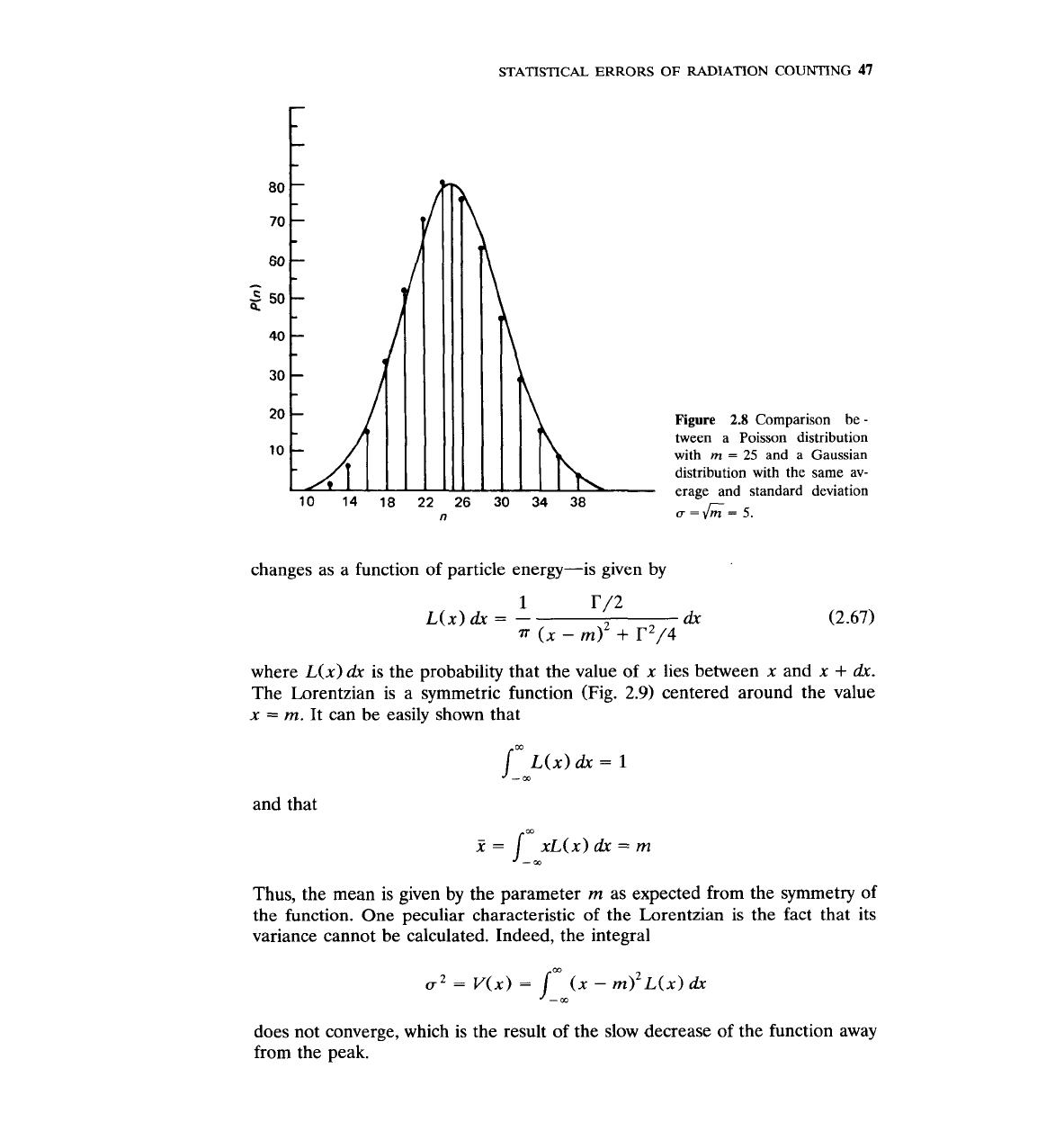
Consider now a Poisson and a Gaussian distribution having the same
average,
m
=
25. Obviously, there is an infinite number of Gaussians with that
average but with different standard deviations. The question one may ask is:
"What is the standard deviation of the Gaussian that may represent the Poisson
distribution with the same average?" The answer is that the Gaussian with
a
=
dk
=
5
is almost identical with the Poisson. Table
2.1
presents values of the
two distributions, and Fig.
2.8
shows them plotted.
The following very important conclusion is drawn from this result:
The outcomes of a series of radiation measurements are members of a Poisson distribution.
They may be treated as members of a Gaussian distribution if the avera e result is more than
m
=
20.
The standard deviation of that Gaussian distribution is
u
=
P
m
.
Use of this conclusion is made in Sec. 2.17, which discusses statistics of
radiation counting.
2.11
THE
LORENTZIAN DISTRIBUTION
The Lorentzian distribution, which describes the resonances of nuclear reactions
-in particular how the probability of interaction (cross section, see Chap.
4)
Table
2.1
Comparison between a Poisson and a Gaussian
Distribution Having the Same Mean
(m
=
25)
G(n) (Gaussian)
n
P,
(Poisson)
o
=
5
10 0.0004
0.0009
12 0.0017
0.0027
14 0.00$.9
0.0071
16 0.0154
0.0168
18 0.03 16
0.0299
20 0.0519 0.0484
22 0.0702
0.0666
24 0.0795
0.0782
25 0.0795
0.0798
26 0.0765
0.0782
28 0.0632 0.0666
30 0.0454
0.0484
3 2 0.0286
0.0299
34 0.0159
0.0168
36
0.0079
0.0071
3
8 0.0035
0.0027
STATISTICAL
ERRORS
OF
RADIATION
COUNTING
47
Figure
2.8
Comparison be
-
tween a Poisson distribution
with
m
=
25
and a Gaussian
distribution with the same av-
erage and standard deviation
34
38
a=&=5.
changes as a function of particle energy-is given by
where
L(x)
dx
is the probability that the value of
x
lies between
x
and
x
+
dx.
The Lorentzian is a symmetric function (Fig.
2.9)
centered around the value
x
=
m.
It can be easily shown that
and that
Thus, the mean is given by the parameter
m
as expected from the symmetry of
the function. One peculiar characteristic of the Lorentzian is the fact that its
variance cannot be calculated. Indeed, the integral
does not converge, which is the result of the slow decrease of the function away
from the peak.
