Tsoulfanidis N. Measurement and detection of radiation

Подождите немного. Документ загружается.

MEASUREMENT

AND DETECTION

RADIATION

Equations 2.12 and 2.13 hold for any number of events, provided the events

are mutually exclusive or stochastically independent. Thus, if we have

such

events xnln=l

,...,

P(x,

...

+xN)

P(xl)

P(x,)

...

+P(xN)

(2.14)

P(x,x,

...

x,)

P(x,)P(x,)

...

P(xN)

(2.15)

2.4

PROBABILITY DISTRIBUTIONS AND RANDOM VARIABLES

When an experiment is repeated many times under identical conditions, the

results of the measurement will not necessarily be identical. In fact, as a rule

rather than as an exception, the results will be different. Therefore, it is very

desirable to know if there is a law that governs the individual outcomes of the

experiment. Such a law, if it exists and is known, would be helpful in two ways.

First, from a small number of measurements, the experimenter may obtain

information about expected results of subsequent measurements. Second, a

series of measurements may be checked for faults. If it is known that the results

of an experiment obey a certain law and a given series of outcomes of such an

experiment does not follow that law, then that series of outcomes is suspect and

should be thoroughly investigated before it becomes acceptable.

There are many such laws governing different types of measurements. The

three most frequently used will be discussed in later sections of this chapter, but

first some general definitions and the concept of the random variable are

introduced.

quantity x that can be determined quantitatively and that in successive

but similar experiments can assume different values is called a random variable.

Examples of random variables are the result of drawing one card from a deck of

cards, the result of the throw of a die, the result of measuring the length of a

nuclear fuel rod, and the result of counting the radioactivity of a sample. There

are two types of random variables, discrete and continuous.

discrete random variable takes one of a set of discrete values. Discrete

random variables are especially useful in representing results that take integer

values-for example, number of persons, number of defective batteries, or

number of counts recorded in a scaler.

continuous random variable can take any value within a certain interval

-for example, weight or height of people, the length of a rod, or the tempera-

ture of the water coming out of a reactor.

For every random variable x, one may define a function f(x) as follows:

Discrete random variables

(xi)

probability that the value of the random variable is xi

1,2,.

. .

where

number of possible (discrete) values of x. Since

takes only one

STATISTICAL ERRORS OF RADIATION COUNTING

value at a time, the events represented by the probabilities f(xi) are mutually

exclusive; therefore, using

Eq.

2.14,

Continuous random variables.

Assume that a random variable may take any

value between a and

b).

Then

f(x)

probability that the value of x lies between x and

One should notice that for a continuous variable what is important is not

the probability that x will take a specific value, but only the probability that x

falls within an interval defined by two values of x. The equation corresponding

to Eq. 2.16 is now

Equations 2.16 and 2.17 give the probability of a sure event, because x will

certainly have one of the values x,, x,,

. .

x, and will certainly have a value

between a and

The function f(x) is called the probability density functionf (pdf).

Consider now the following function:

For a discrete variable,

Thus,

F(x,)

probability that the value of x is less than or equal to xi

The function F(x) is called the cumulative distribution function* (cdf). The cdf

has the following properties:

The cdf is a positive monotonously increasing function,

i.e., F(b)

F(a), if

a. There is a relationship between the cdf and the pdf obtained from Eq.

?It has also been called the frequency function.

'1t has also been called the integral or total distribution function.

MEASUREMENT

AND DETECTION

RADIATION

2.18, namely,

2.5

LOCATION INDEXES (MODE, MEDIAN, MEAN)

If the distribution function

F(x)

f(x)

is known, a great deal of information

can be obtained about the values of the random variable

Conversely, if

F(x)

f(x)

is not completely known, certain values of

provide valuable informa-

tion about the distribution functions. In most practical applications the impor-

tant values of

are clustered within a relatively narrow interval. To obtain a

rough idea about the whole distribution, it is often adequate to indicate the

position of this interval by "location indexes" providing typical values of

In theory, an infinite number of location indexest may be constructed, but

in practice the following three are most frequently used: the mode, the median,

and the mean of a distribution. Their definitions and physical meanings will be

presented with the help of an example.

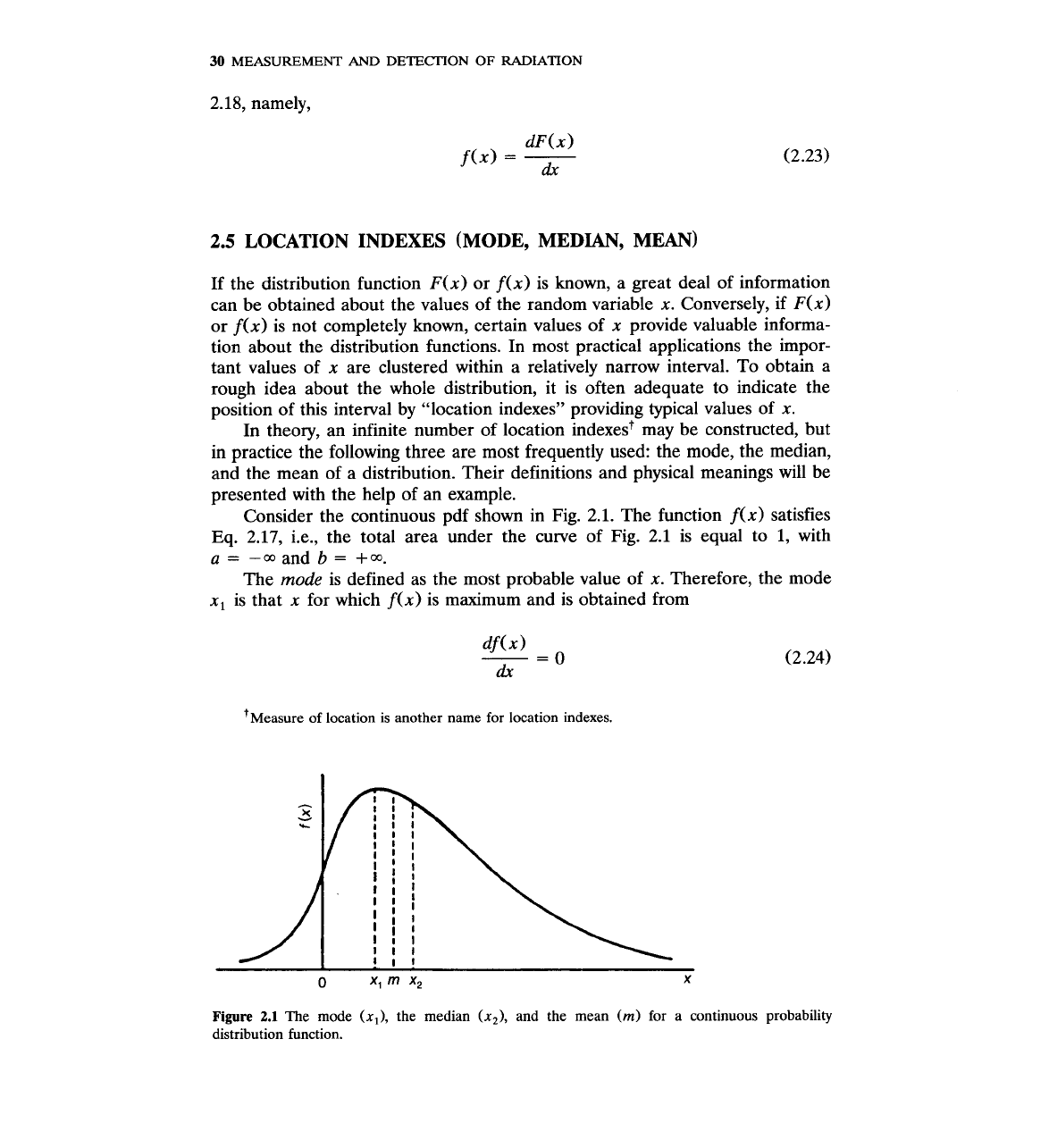
Consider the continuous pdf shown in Fig. 2.1. The function

f(x)

satisfies

Eq. 2.17, i.e., the total area under the curve of Fig. 2.1 is equal to 1, with

-ma nd

+a).

The

mode

is defined as the most probable value of

Therefore, the mode

is that

for which

f(x)

is maximum and is obtained from

'Measure of location is another name for location indexes.

Figure

2.1

The mode

(x,),

the median

(x,),

and the mean

(m)

for a continuous probability

distribution function.

STATISTICAL ERRORS

RADIATION COUNTING

The

median

is the value

for which

i.e., the probability of

taking a value less than

is equal to the probability of

taking a value greater than

x,.

The mean, also known as the "average" or the "expectation value" of

defined by the equation

expression more general than Eq. 2.26 that gives the mean or average of

any function

g(x),

regardless of whether or not

f(x)

satisfies Eq. 2.17, is

For a discontinuous pdf, the location indexes are defined in a similar way. If

the pdf satisfies Eq. 2.16, the mean is given by

Equation 2.28 is an approximation because the true mean can only be deter-

mined with an infinite number of measurements. But, in practice, it is always a

finite number of measurements that is available, and the average

ji.

instead of

the true

is determined. Equation 2.28 is analogous to Eq. 2.2, which defines

the probability based on a finite number of events.

The general expression for the average of a discontinuous pdf, equivalent to

Eq. 2.27, is

Which of these or some other location indexes one uses is a matter of

personal choice and convenience, depending on the type of problem studied.

The mean is by far the most frequently used index, and for this reason, only the

mean will be discussed further.

MEASUREMENT

AND

DETECTION

RADIATION

Some elementary but useful properties of the mean that can be easily

proven using Eqs. 2.26 or 2.28 are

AX=M=

am a

constant

Example

2.5

Calculation of the mean. The probability that a radioactive

nucleus will not decay for time

is equal to

where

is a constant. What is the mean life of such a nucleus?

Answer

Using Eq. 2.26, the mean life

Example

2.6

Consider the throw of a die. The probability of getting any

number between

and 6 is

What is the average number?

Answer

Using Eq. 2.29,

Example

2.7

Consider an experiment repeated N times giving the results

xiIi=l,,,,,~.

What is the average of the results?

Answer

Since the experiments were identical, all the results have the same

probability of occurring, a probability that is equal to 1/N. Therefore, the

mean is

Equation 2.31 defines the so-called arithmetic mean of a series of

random

variables. It is used extensively when the results of several measurements of the

same variable are combined.

extension of Eq. 2.31 is the calculation of the "means of means."

Assume that one has obtained the averages

Z,,

f,,

. .

by performing a

series of

measurements, each involving

N,,

events, respectively.

STATISTICAL

ERRORS

RADIATION

COUNTING

The arithmetic mean of all the measurements, X, is

where

2.6

DISPERSION INDEXES, VARIANCE, AND

STANDARD DEVIATION

pdf or cdf is determined only approximately by any location index. For

practical purposes it is sufficient to know the value of one location index-e.g.,

the mean-together with a measure indicating how the probability density is

distributed around the chosen location index. There are several such measures

called

dispersion indexes.

The dispersion index most commonly used and the only

one to be discussed here is the variance V(x) and its square root, which is called

the standard deviation

The variance of a pdf is defined as shown by Eqs. 2.33 and 2.34. For

continuous distributions,

For discrete distributions,

V(x)

(xi

m12f(xi)

(2.34)

It is assumed that f(x) satisfies Eq. 2.16 or 2.17 and

is a large number. It is

worth noting that the variance is nothing more than the average of (x

mI2.

The variance of

linear function of x, a

bx, is

V(a

bx)

b2v(x)

(2.35)

where a and

are constants.

2.7

COVARIANCE

AND

CORRELATION

Consider the random variables XI, X2,

. . .

X, with means m,, m,,

. . .

and

variances u:, u;,

. . .

ui.

question that arises frequently is, what is the

average and the variance of the linear function

a,X,

a2X2

+aMXM (2.36~)

where the values of aili,

are constants?

MEASUREMENT AND DETECTION

RADIATION

The average is simply (using Eq. 2.28)

The variance is

The quantity

(Xi

mi)(X,

m,) is called the "covariance" between Xi

and X,:

cov(Xi, X,)

(Xi

mi)(X,

m,) (2.38)

The covariance, as defined by Eq. 2.38, suffers from the serious drawback that

its value changes with the units used for the measurement of

Xi,

X,.

eliminate this effect, the covariance is divided by the product of the standard

deviations

ui, 9, and the resulting ratio is called the correlation coefficient

p(Xi, Xi). Thus,

Using Eq. 2.39, the variance of

becomes

Random variables for which pij

are said to be uncorrelated.

If the Xi's are mutually uncorrelated, Eq. 2.40 takes the simpler form

Consider now a second linear function of the variables XI, X2, X,,

XM,

namely,

blXl

...

bMXM. The average of

STATISTICAL

ERRORS

RADIATION

COUNTING

The covariance of

If all the X's are mutually uncorrelated, then

pi,

0 and

If all the X's have the same variance

a2,

Equations 2.40-2.44 will be applied in Sec. 2.15 for the calculation of the

propagation of errors.

2.8

THE

BINOMIAL DISTRIBUTION

The

binomial distribution

is a pdf that applies under the following conditions:

The experiment has two possible outcomes,

and

2. The probability that any given observation results in an outcome of type

is constant, independent of the number of observations.

The occurrence of a type

event in any given observation does not affect the

probability that the event

will occur again in subsequent observations.

Examples of such experiments are tossing a coin (heads or tails is the outcome),

inspecting a number of similar items for defects (items are defective or not), and

picking up objects from a box containing two types of objects.

The binomial distribution will be introduced with the help of the following

experiment.

Suppose that a box contains a large number of two types of objects, type

and type

Let

probability that an object selected at random from this box is type

probability that the randomly selected object is type

MEASUREMENT

AND

DETECTION

RADIATION

experimenter selects

objects at random.+ The binomial distribution,

giving the probability

that

out of the

objects are of type A, is

Example

2.8

A box contains a total of 10,000 small metallic spheres, of

which 2000 are painted white and the rest are painted black.

person removes

100 spheres from the box one at a time at random. What is the probability that

10 of these spheres are white?

Answer

The probability

picking one white sphere is

The probability that

out of 100 selected spheres will be white is, according to

Eq.

2.45,

Example

2.9

A coin is tossed three times. What is the probability that the

result will be heads in all three tosses?

Answer

The probability of getting heads in one throw is 0.5. The probability

of tossing the coin three times

3) and getting heads in all three tosses

3) is

Of course, the same result could have been obtained in this simple case by using

the multiplication law,

Eq.

2.13:

P(heads three times)

(0.5)(0.5)(0.5)

0.125

It is easy to show that the binomial distribution satisfies

The mean

equal to

'1t is assumed that the box has an extremely large number of objects so that the removal of

of them does not change their number appreciably, or, after an object is selected and its type

recorded, it is thrown back into the box. If the total number of objects is small, instead of

Eq.

2.45,

the hypergeometric density function should be used (see Johnson

Leone and Jaech).

STATISTICAL ERRORS

RADIATION

COUNTING

The variance

V(n)

The standard deviation

Figure 2.2 shows three binomial distributions for

10 and

0.1, 0.4, and

0.8. Notice that as

0.5, the distribution tends to be symmetric around the

mean.

2.9

THE POISSON DISTRIBUTION

The Poisson distribution applies to events whose probability of occurrence is

small and constant. It can be derived from the binomial distribution by letting

N+m

P+O

in such a way that the value of the average

stays constant. It is left as

an exercise for the reader to show that under the conditions mentioned above,

the binomial distribution takes the form known as the Poisson distribution,

where

is the probability of observing the outcome

when the average for a

large number of trials is

The Poisson distribution has wide applications in many diverse fields, such

as decay of nuclei, persons killed by lightning, number of telephone calls

received in a switchboard, emission of photons by excited nuclei, and appear-

ance of cosmic rays.

Example

2.10

radiation detector is used to count the particles emitted by

a radioisotopic source. If it is known that the average counting rate is 20

counts/ min, what is the probability that the next trial will give 18 counts/min?

Answer

The probability of decay of radioactive atoms follows the Poisson

distribution. Therefore, using

Eq.

2.50,

That is, if one performs 10,000 measurements,

844

of them are expected to give

the result 18 counts/min.