Tsoulfanidis N. Measurement and detection of radiation
Подождите немного. Документ загружается.


368
MEASUREMENT AND DETECTION OF RADIATION
Figure
11.7
A
Gaussian folded with a Gaussian gives a third Gaussian, which has a larger width.
Example
11.8
The source spectrum is a Lorentzian centered at
E,:
and the response function is also a Lorentzian with width
r.
What is the
measured spectrum?
Answer
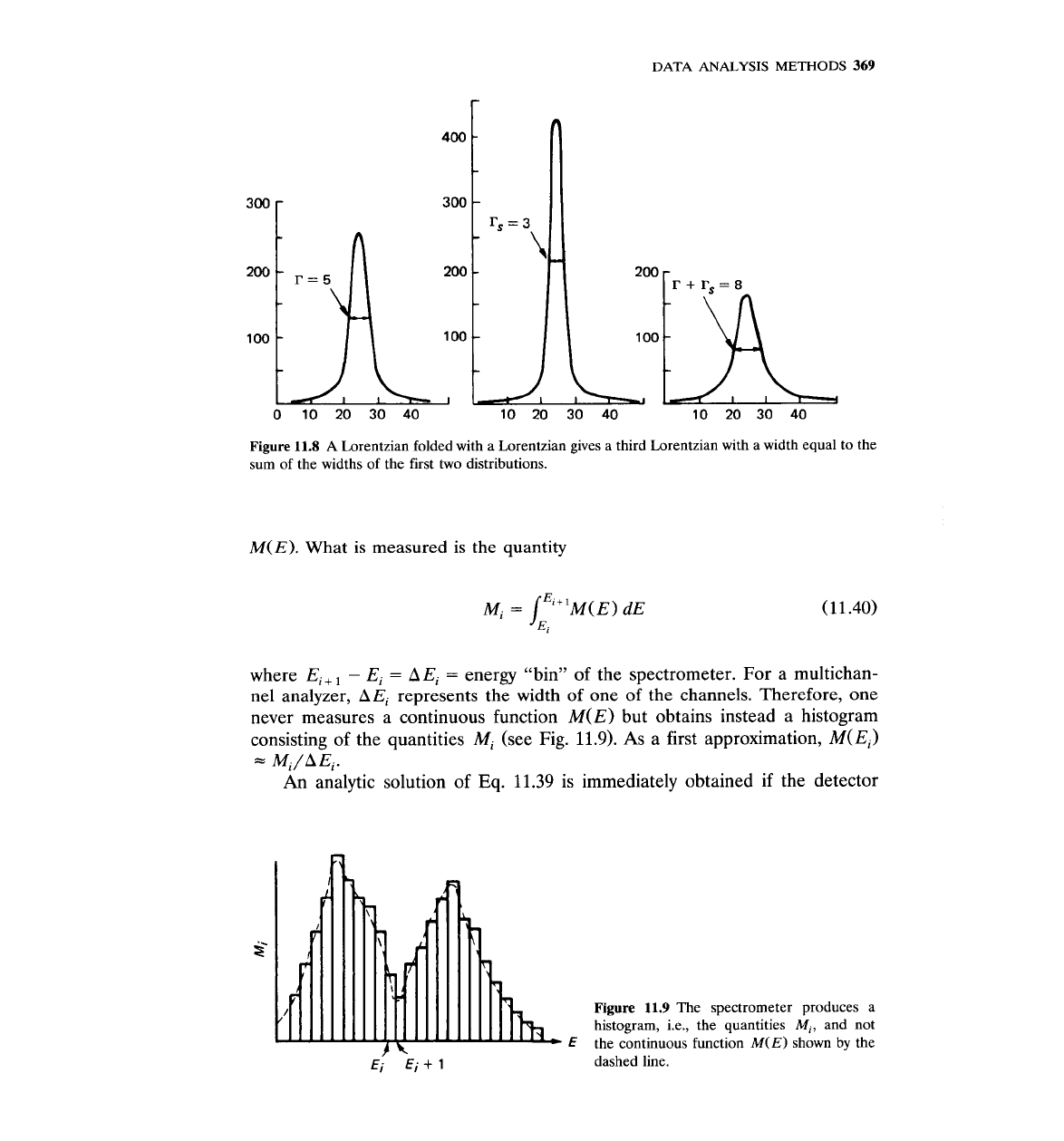
Figure
11.8
shows the three functions involved. Notice that by folding a
Lorentzian with a Lorentzian, the result is a third Lorentzian with width equal
to the sum of the two widths.
11.5.2
The General Method of Unfolding
This section discusses methods of unfolding, assuming that an energy spectrum
is measured with a multichannel analyzer or any other device that divides the
measured spectrum into energy bins. As stated at the beginning of Sec.
11.5,
unfolding means to solve the Fredholm-type integral equation
M(E)
=
/IR(E, EWE') d~'
(11.39)
0
for the unknown function
S(E).
Before possible methods of solution of Eq.
11.39
are discussed, it is important to note that no spectrometer measures
DATA
ANALYSIS
METHODS
369
Figure
11.8
A
Lorentzian folded with a Lorentzian gives a third Lorentzian with a width equal to the
sum of the widths of the first
two
distributions.
M(E). What is measured is the quantity
where E,,,
-
E,
=
AE,
=
energy "bin" of the spectrometer. For a multichan-
nel analyzer, AE, represents the width of one of the channels. Therefore, one
never measures a continuous function M(E) but obtains instead a histogram
consisting of the quantities Mi (see Fig. 11.9). As a first approximation, M(E,)
=
M,/AE,.
An
analytic solution of Eq. 11.39 is immediately obtained if the detector
Figure
11.9
The spectrometer produces a
histogram, i.e., the quantities
Mi,
and not
E
the continuous function
M(E)
shown
by
the
E,:
E;
+
1
dashed line.

370
MEASUREMENT AND DETECI'ION
OF
RADIATION
Figure
11.10
A
step-function response.
E'
response is a 6 function. Indeed, if R(E, E')
=
6(E
-
E'), then
This case is not encountered in practice because there is no detector with such a
response function; it indicates only that with perfect energy resolution there is
no need for unfolding. In general, the more the detector response resembles a
Sfunction, the more the measured spectrum looks like the source spectrum.
A
second type of response that gives an analytic solution, in principle, is a
step functiont (Fig 11.10). Let
R(E,E1)
=
O<EsE1
otherwise
where
C
is a normalization constant. Then Eq. 11.39 takes the form
The lower limit of the integral has been set equal to E because if the response
function is that given by Eq. 11.41, no source particles with energy E'
<
E can
contribute to M(E). Upon differentiation,'-4 Eq. 11.42 gives
which is the desired solution. This method of unfolding is known as the
differentiation method.
Since only the quantities
Mi
(Eq. 11.40) are obtained, and not the function
M(E), the differentiation indicated by Eq. 11.43 must be performed numerically.
There are several computer codes that perform such differentiation.
h he
response of proton-recoil counters resembles
a
step function (see Chap.
14).

DATA
ANALYSIS
METHODS
371
The most general method of unfolding is based on a transformation of Eq.
11.39 into a matrix equation. Equation 11.39 may be rewritten as
where the integral over
E'
has been written as a sum of integrals over
NR
energy intervals
AE,
=
E,,,
-
E,.
Next, Eq. 11.44 is integrated over
E
to give
(see Eq. 11.40)
Equation 11.45 is still exact. To proceed further, one needs an approximation
for
the source spectrum
S(E).
Two approximations and corresponding methods
of solving the resulting matrix equation are presented in the next two sections.
11.5.3
An Iteration Method of Unfolding
There are several iteration methods. The method presented here is useful for
slowly varying spectra and has been used successfully to unfold beta spectra.'
The source spectrum
S(E)
is approximated over any interval
AEj
by the
expression
si
S(E1)
=
-
AE,
Using Eq. 11.46 and defining
then Eq. 11.45 takes the form
or, in matrix notation,
M=R-S
A
formal solution of
Eq.
11.49 is
where
R-'
is the inverse of the matrix with elements given by Eq. 11.47.
Although in principle,
Eq.
11.50 represents a solution to the unfolding problem,
in practice the matrix inversion is not always achieved or leads to a solution with
a large error.

372
MEASUREMENT
AND
DETECTION
OF
RADIATION
The iteration method to be discussed here starts with
Eq.
11.48
and uses the
measured spectrum as the first guess of the iteration pr~cedure.~
This source spectrum when substituted into
Eq.
11.48
gives
The error of
Sj')
is taken to be
S.-S!~)=M.-M.(~) j=1,~~
I I
I
I
and the new guess for the second iteration is
S!2)
=
+
[Mi
-
~,.(l)]
j
=
1,
NR
I I
Substitution into
Eq.
11.48
gives
M!~)=~R~~s~(~)
I
i=l,NR
and so on. The nth iteration uses
s!")
=
s!"
-
1)
+
[M
-
~.(n
-
1)
I
I
I
I
]
j=l,NR
and is the solution to the problem if the difference
I
Mj
-
Mi(")[
for
j
=
1,.
. . ,
NR
is acceptably small. This iteration method converges in less than five iterations
and gives good results.
11.5.4
Least-Squares
Unfolding
A
different approximation for the source spectrum, used with neutrons, assumes
that
S(E)
can be represented as a sum of
NS
discrete
component^.^-^
There-
fore, one can write
NS
S(Et)
=
C
XjS(Et
-
E,)
(11.51)
j=
1
Using
Eq.
11.5 1
and defining
then
Eq.
11.45
takes the form
or in matrix notation,

DATA
ANALYSIS
METHODS
373
If
NR
=
NS,
the formal solution of Eq. 11.54 is, as with Eq. 11.49,
Because of the difficulties of matrix inversion, a least-squares solution has been
attempted with
NR
>
NS.
If
NR
<
NS,
no unique solution exists, but an
acceptable one has been obtained.
The least-squares unfolding starts with
Eq.
11.53
and minimizes the quantity
The weighting factors wi are usually taken to be the inverse of the variance of
Mi. The minimization is achieved by setting
which gives
and can be solved for
X,
for
j
=
1,
NS.
Equation 11.57 may be written in matrix
form6
where
=
transpose of
A.
Computer round-off errors in completing the matrix inversion shown by Eq.
11.58
lead to large oscillations in the solution
X.
The oscillations can be reduced
if the least-squares solution is "constrained." Details of least-squares unfolding
with constraints are given in Refs.
6
and
7.
11.6
DATA
SMOOTHING
The smoothing of raw experimental data is a controversial subject because it
represents manipulation of the data without clear theoretical justification.
However, smoothing is generally accepted as common practice, since experience
has shown that it is beneficial in certain cases to the subsequent analysis of the
data, for example, in identification of energy peaks in complex gamma energy
spectra (Chap.
12)
and unfolding of neutron energy spectra (Chap. 14). Data
smoothing should be viewed as an attempt to filter out the statistical fluctua-
tions without altering the significant features of the data.
To illustrate how data smoothing is performed, consider again
N
measure-
ments yili=
1,N,
where y,
=
y(xi). Smoothing, which is applied to the values of y,,
is an averaging process. In the simplest case, one adds a fixed odd number of yi

374
MEASUREMENT
AND
DETECI'ION
OF
RADIATION
values, takes the arithmetic average of the sum, and sets the smoothed value of
yi
at the center of the group equal to this average. Next, the first point of the
group is dropped, the next point is added at the other end of the group, and the
process is repeated for all
yi
points. In general, the "smoothing" equation takes
the form
1
j=n
where
C,
=
coefficients that depend on the method of smoothing (see below)
M
=
normalization constant
n
=
index showing the number of points used in the smoothing process
(the index
n
means that
2n
+
1
points were used for smoothing)
y,
=
smoothed value, replacing the old
y,
in the middle of
2n
+
1
points
The coefficients
C,
are determined by least-squares fitting a polynomial of
I
order
m
to
2n
+
1
data points9-" and taking the smoothed value equal to the
value of the polynomial in the middle point (Fig. 11.11). To illustrate the
method, a few examples are given below. The least-squares fit will be based on
Eqs. 11.18-11.20.
Three-point
zeroth-order
smoothing.
From
Eq.
11.18,
f(x)
=
a,
From Eq. 11.19,
3
A,,
=
Cwi=
El
=3
i=
1
i
From Eq. 11.20,
3 3
B~
=
Cwiyi
=
C
yi
1
i=
1
From Eq. 11.16,
B,
1
3
a,
=-=-Cy.
'11
3
i=l
(2n
+
1)
Data points
-
Polynomial of
i.'
degree
m
Figure
11.11
Data smoothing.
A
polynomial of degree
m
is fitted
to
(2n
+
1)
data points, and the
smoothed value is equal to the
value of the polynomial in the
111111
x
middle point.

DATA
ANALYSIS
METHODS
375
Therefore, if three-point zeroth-order smoothing is applied (Fig.
11.121,
the
constants of
Eq.
11.59
are
M=3
Cl=C2=C3=1
and
y.
1
=
i(
3
Yi-I
+~i +~i+l)
Five-point zeroth-order smoothing.
Following the same
s
obtains
M=5 Ci=l
i=1,5
and
y.
r
=
i(
5
Yi-2
+
Yi-I
Yi
+Yi+l
+~i+2)
;teps as above, one
Three-point first-order smoothing.
From Eq.
11.18,
f(x)
=
a,
+
a,x.
Using
Eqs.
11.19, 11.20,
and
11.16,
one can solve for the values of
M
and
Ci.
If the
xi
points are equally spaced, the result is identical with three-point zeroth-order
smoothing (Eq.
11.60).
This is true, in general, for equally spaced
xi;
that is, the
result of smoothing with an even-order polynomial is the same as that with a
polynomial of the next higher order. Table
11.2
gives the values of
M
and
C,
for
second-order smoothing.
As an example of using the various equations, Fig.
11.13
shows results of
three-point zeroth-order smoothing and five-point second-order smoothing, i.e.,
using Eqs.
11.60
and
11.62:
If the total number of points is N, the number of smoothed points is
N
-
2n
for
(2n
+
1)-point smoothing because the first smoothed point is
i
=
n
+
1
and the last one is N
-
n.
The smoothing process can be repeated if
necessary-i.e., one may smooth data that were previously sm~othed.~
1..
Figure
11.12
Three-point, zeroth-order smoothing.

376
MEASUREMENT
AND
DETECTION
OF
RADIATION
Table
11.2
Coefficients for Second-Order Smoothingt
f~rom reference
9.
One of the difficulties in data smoothing is the choice of the correct value
for
n.
Unfortunately, there are no strict criteria for the selection of
n.
The
analyst should be guided mainly by experience and by the general effects of
smoothing on the results. In particular, if the data represent energy spectra with
many peaks, the smoothed spectrum may tend to flatten the peaks and fill the
valleys.
50
45
--
40
--
35
--
30
--
Yi
25
--
20
--
15
--
lo
--
Figure
11.13
The same data smoothed with two different equations. Circles are original data,
squares are data smoothed with Eq. 11.60, and crosses are data smoothed with Eq. 11.62.

DATA
ANALYSIS
METHODS
377
The general smoothing equation may be written as
which has the same form as the folding-unfolding matrix equations (Eq. 11.48).
Thus, smoothing may be considered as folding the data (y,) with the weights
(Ri-
,)
as the response function. Taking it one step further, one may perform
smoothing by using a continuous function, i.e., a Gaussian. Then
The operation indicated by Eq. 11.64 has been applied to neutron spectroscopic
data.12
PROBLEMS
11.1
The table below shows radioactive decay data from a certain isotope. Using least-squares fit,
determine the half-life of the isotope. What is the error of the half-life as determined by this set of
data?
t(rnin) Counts t(min) Counts
11.2
The numbers below represent values of cosine for the corresponding angles.
Angle:
5'
10"
15" 20"
25"
3
0"
Cosine:
0.99619 0.98481
0.96593 0.93969 0.90631 0.86603
Obtain cosine values, by interpolation, for 22" using Lagrange's three-point interpolation formula.
Evaluate the error of your result. Compare the error with its correct value.
11.3
Prove Eqs. 11.22 to 11.24.
11.4
Obtain the least-squares fit equations for a quadratic fit.
11.5
Prove that the result of folding a step function with a Gaussian is
where the source spectrum is
E
2
E,
S(E)
=
(?
otherwise
