Tsoulfanidis N. Measurement and detection of radiation
Подождите немного. Документ загружается.

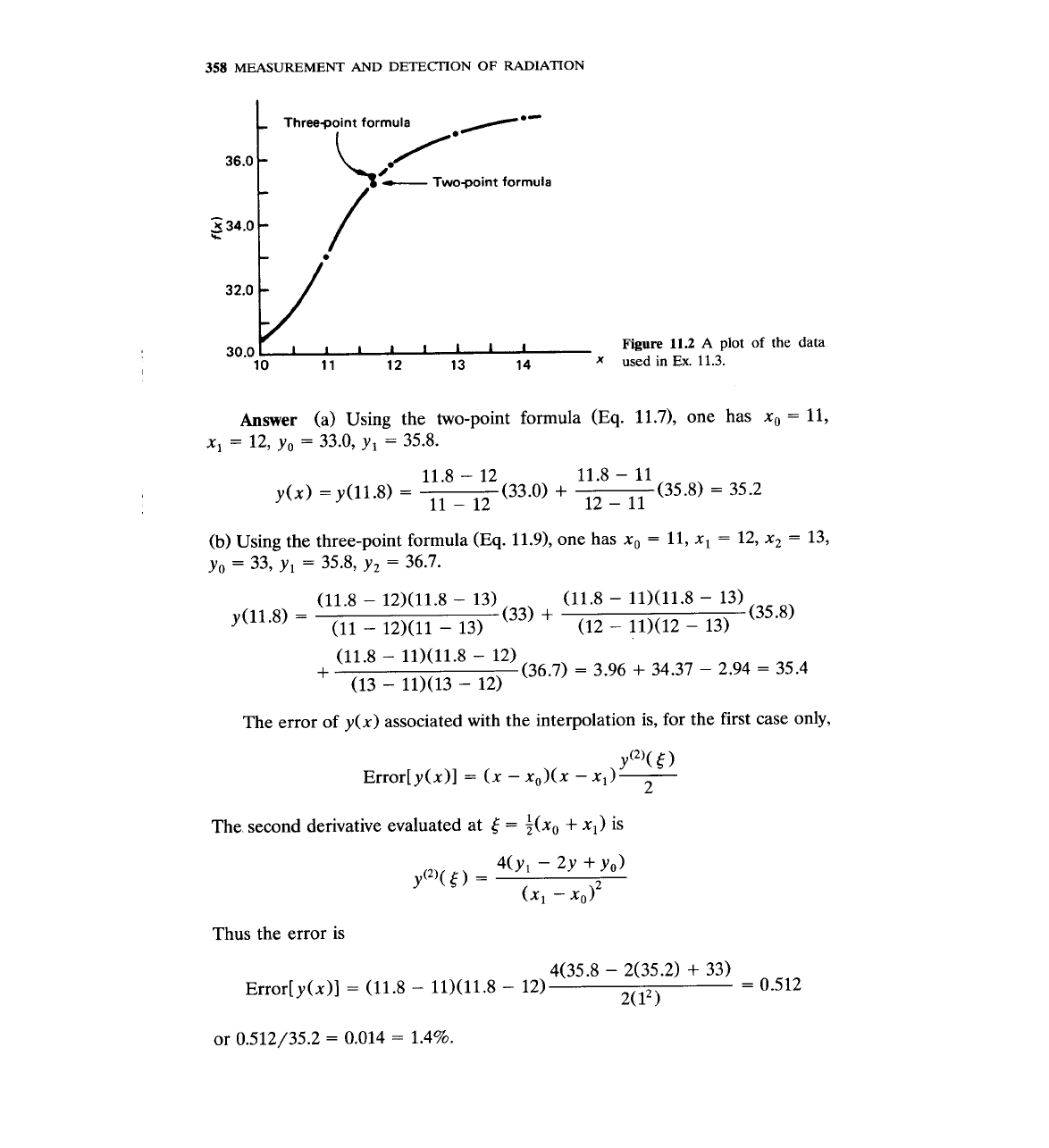
358
MEASUREMENT
AND
DETECTION
OF
RADIATION
Figure
11.2
A
plot
of
the
data
used
in
Ex.
11.3.
Answer
(a) Using the two-point formula
(Eq. 11.7),
one has
xo
=
11,
x,
=
12, yo
=
33.0, y,
=
35.8.
(b)
Using the three-point formula
(Eq. 11.9),
one has
xo
=
11, x,
=
12, x2
=
13,
yo
=
33, y,
=
35.8, y2
=
36.7.
The error of
y(x)
associated with the interpolation is, for the first case only,
The second derivative evaluated at
6
=
i(xo
+
x,)
is
Thus the error is

DATA
ANALYSIS
METHODS
359
11.4
LEAST-SQUARES FITTING
Assume that an observer obtained the experimental data yi
=
y(xi)li=
1;~.
It is
often desirable to find a function that can represent the data, i.e., to find a
function that can be fitted to the data. Let such a function be written as
fxaa 2,...,aM
M<N
where a,l,=
1,~
are parameters to be determined. According to the method of
least squares, the best values of the parameters a, are those that minimize the
quantity
N
Q
=
C
wi[yi -f(x,)12
(11.10)
i=
1
where wili=l,N are weighting functions. Minimization of
Q
is achieved by
requiring
dQ
--
-
0
rn
=
1,
...,
M
'am
Before
Eq.
11.11 is solved, it should be pointed out that the observer
decides about the form of the function f(x) and the weighting functions wi. The
form of f(x) is obtained by the curve-fitting methods discussed in Sec.
11.2.
The
weighting functions are selected based on the type of data and the purpose of
the fit. For example, if the data are the result of a counting experiment,
wi
=
1/ai2, where
ai
is the standard deviation of
yi.
There are two types of least-squares fit, linear and nonlinear. Linear
least-squaresfit is based on a function f(x) of the form
where the +,(x) are known functions of x.
Nonlinear least-squares fit is based on
such as
a function f(x) nonlinear in a,,
f(x, a,, a,,
.
.
.
,
a,)
=
a, cos(a2x)
The interested reader should consult the bibliography of this chapter (see
Bevington) for further information on nonlinear least-squares fit.
For a linear least-squares fit, the parameters
amlm=
,,
are determined
from
Eq.
11.11, with
Eq.
11.12 giving the form of f(x). The result is
If one defines

360
MEASUREMENT
AND
DETECTION
OF
RADIATION
and
then Eq.
11.13
takes the form
Equation
11.16
forms a system of
M
linear nonhomogeneous equations for the
M
unknowns
a,l,=
and can be solved by using any of the standard methods
(e.g., Kramer's rule). In matrix notation, the solution is
where
A
and
B
are matrices with elements given by Eqs.
11.14
and
11.15.
If the function
f(x)
is a polynomial, then
M
f(x, a,, a,,
. .
.
,
am)
=
x
amxm-'
(11.18)
m=l
Equations
11.14
and
11.15
take the form [since
+k(~)
=
xk-
'
1
Akm
=
C
wiX;-
lxy
-
I
(11.19)
i
B,
=
~wiyix"
-'
(11.20)
1
The notation used in Eqs.
11.19
and
11.20
and in the next section is
C:
,
-+
Xi.
11.4.1
Least-Squares Fit
of
a Straight Line
If the function represented by Eq.
11.18
is a straight line, then
f(xi, a,, a,)
=
a,
+
a2xi
Thus, Eqs.
11.19
and
11.20
become
A,,
=
Cw,
AI2
=
wixi
=
A2'
A2,
=
Ewix?
1
i i
B,
=
wiyi B,
=
Cwiyixi
i
t
Then, Eq.
11.16
takes the forms
Allai
+
Al,a2
=
B,
A,,
a1
+
A22a2
=
B2

DATA
ANALYSIS
METHODS
361
which are solved to give
1
a2
=
[(
f
wi)
(
f
WiYiXi)
-
(ii)
(Y)]
(11.23)
and
The variance of
a,
and
a,
is obtained by using the principle of propagation of
error presented in Chap.
2.
where
a,,
=
standard error of
yi
=
ui.
In many cases, the standard deviation of
yi
defines the weighting functions,
and specifically, analysts use
Then,
Eq.
11.25
gives
where
D
is given by Eq.
11.24
with
wi
=
1/ui2.
Equations
11.22-11.27
are
further simplified if all the
ui
have the same value.
11.4.2
Least-Squares Fit
of
General Functions
A
straight-line least-squares fit is not limited to linear functions of
x.
It may be
used with functions such as the exponential
(y
=
aebx)
or the power relationship
(y
=
axb)
after an appropriate transformation of variables. For example, the
exponential function can be written as
In
y
=
In
a
+
bx
which is of the form given by Eq.
11.21
after setting
y'
=
In
y
a;
=
In
a
a;
=
b

362
MEASUREMENT
AND DETECTION
OF
RADIATION
When the variable is transformed, it is necessary to obtain the standard
deviation of the new variable. In general, if one sets
then the standard deviation of yl(x) is
In the example given above, y'
=
In y and
Therefore, if a transformation is applied to the function, all the
ui
in Eqs.
11.26
and
11.27
should be replaced by the values given by Eq.
11.30.
If the parameters a, are transformed, the standard deviation of the new
constant is again determined by Eq.
11.29.
In the example given above, a'
=
In a
and
Table
11.1
presents a number of functions that can be cast into a linear (or
polynomial) form by a transformation of variables. It should be emphasized that
although the functions shown in Table
11.1
are not linear in x, the least-squares
fit is still linear.
An
example of a function f(x, a,,
.
.
.
)
that represents a
nonlinear least-squares fit is
f(x, a,, a,,
. .
.)
=
a, cos(a,x)
Example
11.4
The
following table gives neutron-absorption cross-section
values and their errors as a function of neutron kinetic energy. Determine the
analytic function that fits this data set.

DATA
ANALYSIS
METHODS
363
Table
11.1
Functions That Can Be Changed into a Form Suitable for a
Linear Least-Squares Fit
Function used in
Function y(x) Transformation
the least-squares fit
y
=
aebx
y'=lny
a'=lna
y'
=
a'
+
bx
Answer
If
one plots the data on log-log paper, the result is very close to a
straight line (see Fig. 11.3). Therefore, the function to use is
If one takes
wi
=
1/ui2 and applies Eqs. 11.22-11.27, the result is
Figure
11.3
The least-squares fit
to the
data
of
Ex.
11.4.

364
MEASUREMENT
AND DETECTION
OF
RADIATION
11.5
FOLDING
AND
UNFOLDING
To define the problems of folding and unfolding, consider the functions
where the function R(x, x') is normalized to 1:
Folding the function
S(x) with the function R(x, x') to obtain the function
M(x) means to perform the integration
Unfolding means to obtain the function S(x), knowing M(x) and R(x, x'). Thus,
folding is an integration, as shown by Eq. 11.33. Unfolding, on the other hand,
entails solving the integral equation, Eq. 11.33-known as the Fredholm equa-
tion-for the unknown function S(x).
In the field of radiation measurements, folding and (especially) unfolding
are very important operations that have to be applied to the experimental data.
In most radiation measurements, the variable x is the energy of the particle, and
for this reason the discussion in this section will be based on that variable. The
reader should be aware, however, that x may represent other quantities, such as
time, velocity, or space variables. If x is the energy of the particle, the functions
S(x), M(x), and R(x, x') have the following meanings (also given in Sec. 9.7):
S(
E) dE
=
source spectrum
=
number of particles emitted by the source
with energy between E and E
+
dE
M(
E) dE
=
measured spectrum
=
number of particles recorded as having
energy between E and
E
+
dE
R(E, E') dE
=
response of the detector =probability that a particle emitted by
the source with energy
E'
will be recorded with energy
between E and
E
+
dE
As
explained in Chap. 9, the response function is measured using monoen-
ergetic sources.
A
monoenergetic source is represented mathematically by the
delta function
(8
function), which has these properties (Fig. 11.4):
l-;6(~
-
E,) dE
=
if El
<
E,
<
E,
0
otherwise

DATA
ANALYSIS
METHODS
365
Thus, the
6
function is equal to zero everywhere except at E
=
E,, which is, of
course, what the energy spectrum of a monoenergetic source represents. Be-
cause of the property expressed
by
Eq.
11.34, integrals involving the 6 function
are immediately evaluated. For any function f(E), one obtains
because there is no contribution to the integral except at
E
=
E,. For the same
reason, if
E,
is outside the limits of integration, then
Assume that a nionoenergetic source emitting
S,
particles per second (Fig.
11.4) is used to measure the response function.
If
one substitutes the expression
for this source,
into
Eq.
11.33, the result is
M(E)
=
ImR(~, E')S,S(E
-
E,) dE'
=
S,R(E, E,)
(11.38)
0
Equation 11.38 shows that the measured spectrum is indeed equal to the
response function in the case of a monoenergetic source.
11.5.1
Examples of Folding
In radiation measurements, folding means to obtain the shape of the measured
spectrum when the source and the detector response are known. Several
examples of folding using a Gaussian distribution as the response function are
presented next.
366
MEASUREMENT
AND
DETECTION OF RADIATION
Example
11.5
The source spectrum is a step function:
What is the measured spectrum?
Answer
where
(
"i:
)
=
error function
=
&
L(E-E.)/~
r2/2
erf
-
e
dt
Figure
11.5
shows the three functions involved.
Example
11.6
The source spectrum is a square spectrum:
El
I
E
I
E2
S(E)
=
otherwise
What is the measured spectrum?
Answer
Figure
11.6
shows the functions involved.
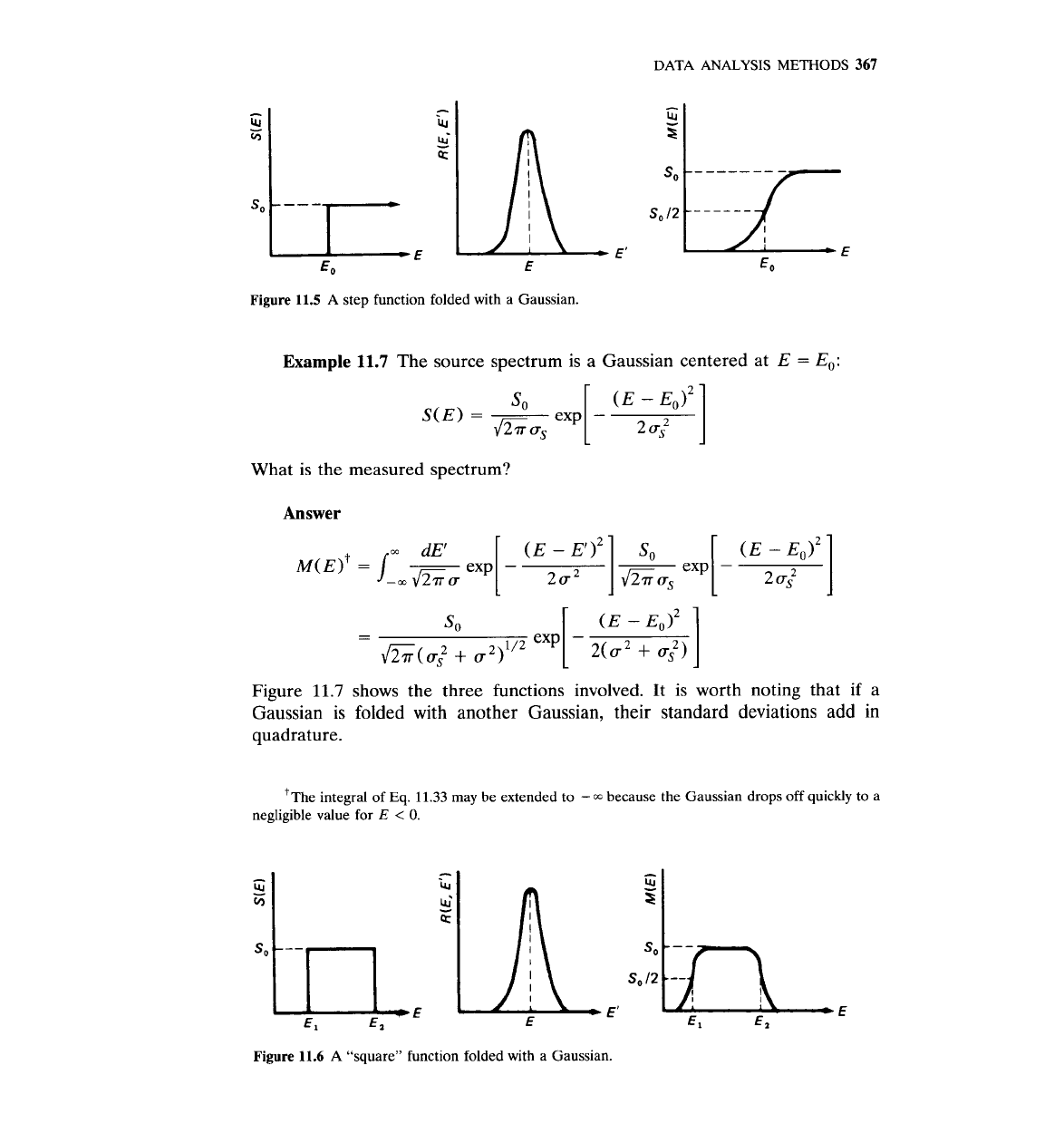
DATA
ANALYSIS
METHODS
367
Figure
11.5
A step function folded with a Gaussian.
Example
11.7
The source spectrum is a Gaussian centered at
E
=
E,:
What is the measured spectrum?
Answer
m
dE'
M(E)'
=
/
7
exp
-m
~TU
Figure
11.7
shows the three functions involved. It is worth noting that if a
Gaussian is folded with another Gaussian, their standard deviations add in
quadrature.
h he
integral of Eq.
11.33
may be extended to
-m
because the Gaussian drops off quickly to a
negligible value for
E
<
0.
Figure
11.6
A
"square" function folded with a Gaussian.
