Троян В.Н. Принципы решения обратных геофизических задач
Подождите немного. Документ загружается.


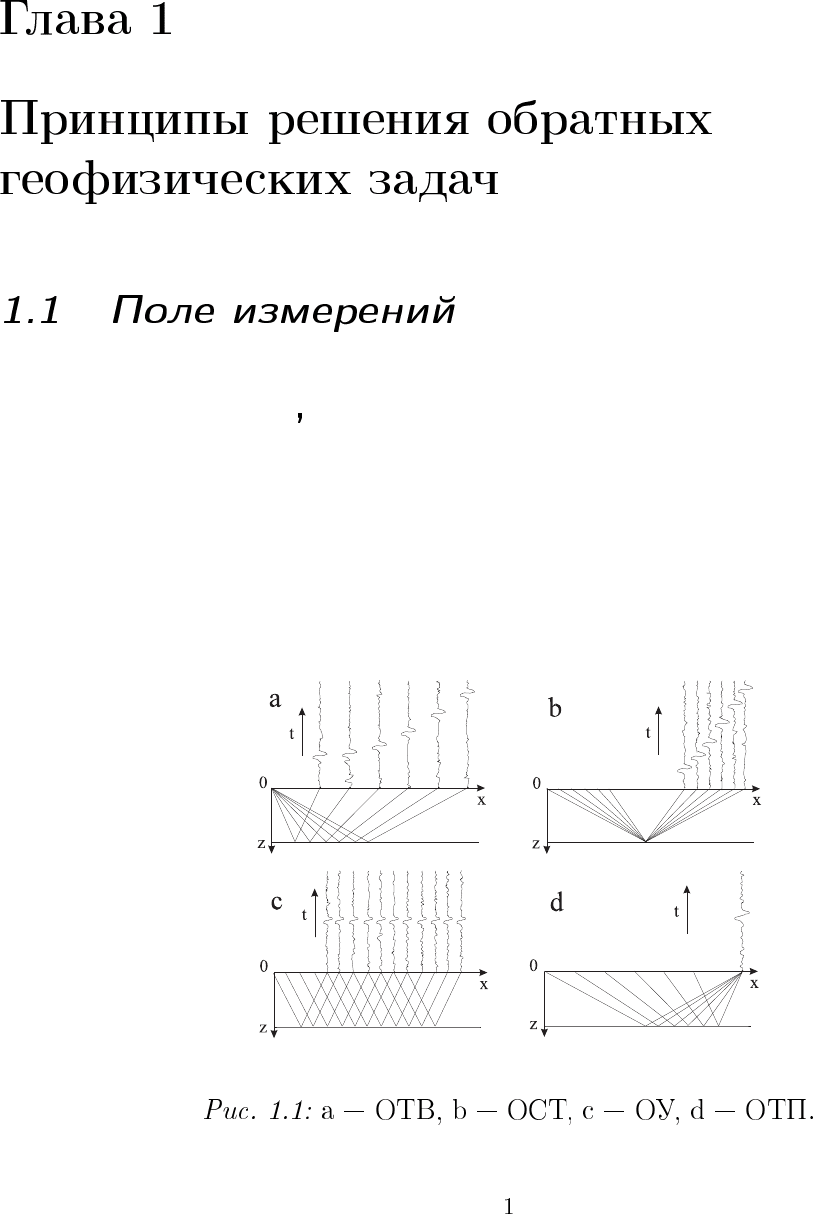
~u(~x, t), ~x ∈ R
3
u
i
=
Z
T
dt
Z
V
dxδ(x
i
− x)h
i
(t
i
− t)(~e
T
(x
i
)~n(x))ϕ(~x, t),
~ϕ(~x, t) = ~nϕ(~x, t)
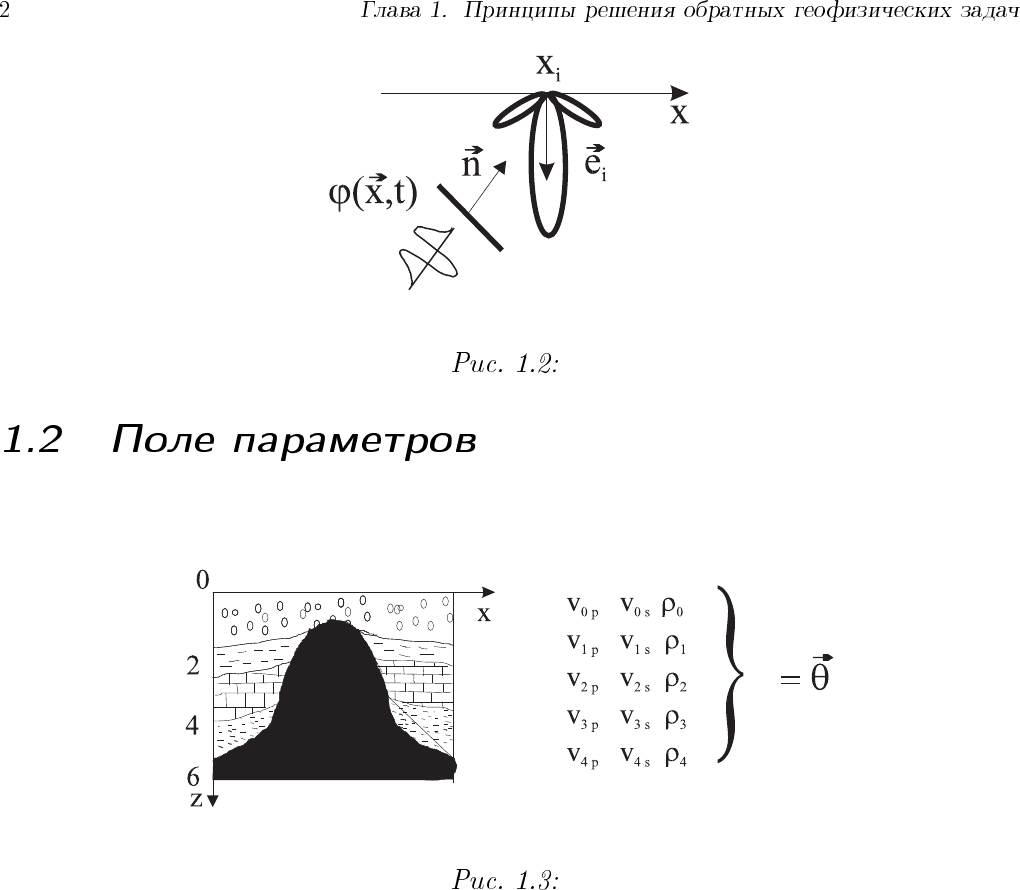
ϕ(~x, t); ~x ∈ R
3
; S(~x, t); θ(~x) ∈ φ(~x)
L
θ
ϕ = S
ϕ(~x, t)|
t=t
0
= ϕ
0
(~x, t), ϕ(~x, t)|
Γ
= ϕ
1
(~x, t)
u = Hϕ + ε
ϕ = L
−1
θ
S
⇒
ˆ
~
θ
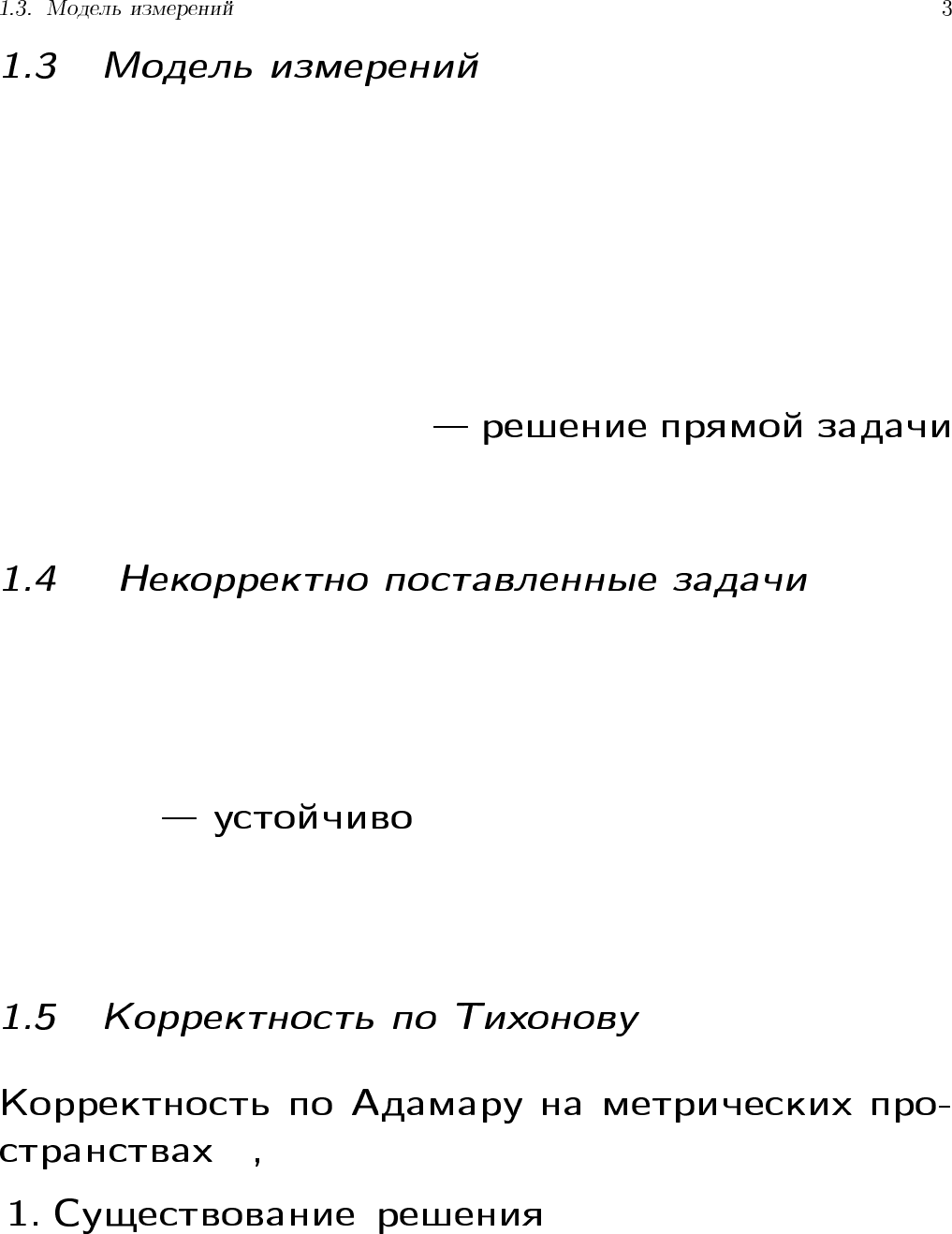
u = P(θ) + ε
P : P(θ) = Hϕ
u = P(θ
0
) + P
′
|
θ
0
δθ + ˜ε
˜ε = ε+O(kδθk
2
); P(θ
0
)
˜ε ∈ N(hεi, K
ε
)
Lϕ = s;
ϕ ∈ φ; s ∈ S
ρ
s
(s
1
, s
2
); ρ
φ
(ϕ
1
, ϕ
2
); s
1
, s
2
∈ S; ϕ
1
, ϕ
2
∈ φ
ϕ = R(s)
ε > 0; δ(ε) > 0
ρ
s
(s
1
, s
2
) ≤ δ(ε) → ρ
φ
(ϕ
1
, ϕ
2
) ≤ ε
ϕ
1
= R(s
1
); ϕ
2
= R(s
2
); s
1
, s
2
∈ S ϕ
1
, ϕ
2
∈ φ
φ S
s ∈ S, ϕ ∈ φ :
ϕ = R(s)

⊓
φ⊂
φ
(
˜ϕ = arg infkLϕ − sk
2
B
∆
=arg inf(Lϕ − s, B(Lϕ − s))
˜ϕ ∈
⊓
φ = kϕk
2
H
∆
=(ϕ, Hϕ) ≤ c
kϕk
2
H
˜ϕ
α
= arg inf{kLϕ − sk
2
B
+ αkϕk
2
H
}
α : k˜ϕ
α
k
2
H
≤ c, α
(L
∗
BL + αH)ϕ = L
∗
Bs
u = P(θ) + ε

J(θ) = J(θ
n
) + (J
′
, θ − θ
n
) + 1/2(θ − θ
n
, J
′′
(θ − θ
n
)) ⇒
⇒ J
′′
(θ − θ
n
) + J
′
⇒ θ
n+1
= θ
n
− [J
′′
n
]
−1
J
′
n
J(θ) = ku − P(θ)k
2
K
−1
ε
+ kθ − θ
0
k
2
K
−1
θ
˜
θ = arg min J(θ) ⇒ θ
n+1
= θ
n
− [J
′′
n
]
−1
J
′
n
J
′′
n
=
δ
2
δθ
2
|
θ
n
J = 2[P
∗
n
K
−1
ε
P
n
+ K
−1
θ
]
δ
δθ
|
θ
n
J = [P
∗
n
K
−1
ε
(u
n
− u) + K
−1
θ
(θ
n
− θ
0
)]
P
n
=
δ
δθ
|
θ
n
P; u
n
= P(θ
n
)
θ
n+1
= θ
n
− [P
∗
n
K
−1
ε
P
n
+ K
−1
θ
]
−1
×
×[P
∗
n
K
−1
ε
(u
n
− u) + K
−1
θ
(θ
n
− θ
0
)]
A
~
θ =
~
b
A
~
θ ≥
~
b
~
θ ∈ N(
~
θ
0
, K
θ
)

I
Geol.
(~x)
P
Petr.
=⇒I
P etr.
(~x)
P
W
(N
w
)
=⇒ φ
W
(~x
s
, ~x
r
, t)
P
H
(N
H
)
=⇒ u(~x
s
, ~x
r
, t) ⇒
P
Proc.
(N
Proc.
)
=⇒ ˜u(~x
0
, t)
P
inv.
(N
inv.
)
=⇒
ˆ
θ
P
(~x)
P
Int.
(N
Int.
)
=⇒
ˆ
G
Imag
(~x)
P
Int
∼ P
−1
P etr
; P
Inv
∼ P
−1
W
-
6
?
?
?
-

~
ξ = (x
1
, x
2
, . . . , x
n
)
g(x
1
, . . . , x
n
)
¯x = (1/n)
n
X
i=1
x
i
.
s
2
= (1/n)
n
X
i=1
(x
i
− ¯x)
2
.
v =
s
¯x
.

~
ξ
~
ξ ∈ f(~x,
~
θ), θ ∈ Ω,
~
θ
F = {f(~x,
~
θ),
~
θ ∈ Ω}
~
ξ
D d d ∈ D
~x ∈ X
~
θ ∈ Ω
X D Ω
~
θ
g(x
1
, . . . , x
n
)
