Троян В.Н. Принципы решения обратных геофизических задач
Подождите немного. Документ загружается.


~x
g(~x)
ˆ
~
θ
n
= g(x
1
, . . . , x
n
).
P (|
ˆ
θ
n
− θ
0
| ≤ ε) ≥ 1 − η,
ε > 0 η > 0
ˆ
θ
n
θ
0
M[
ˆ
θ
n
−θ
0
]
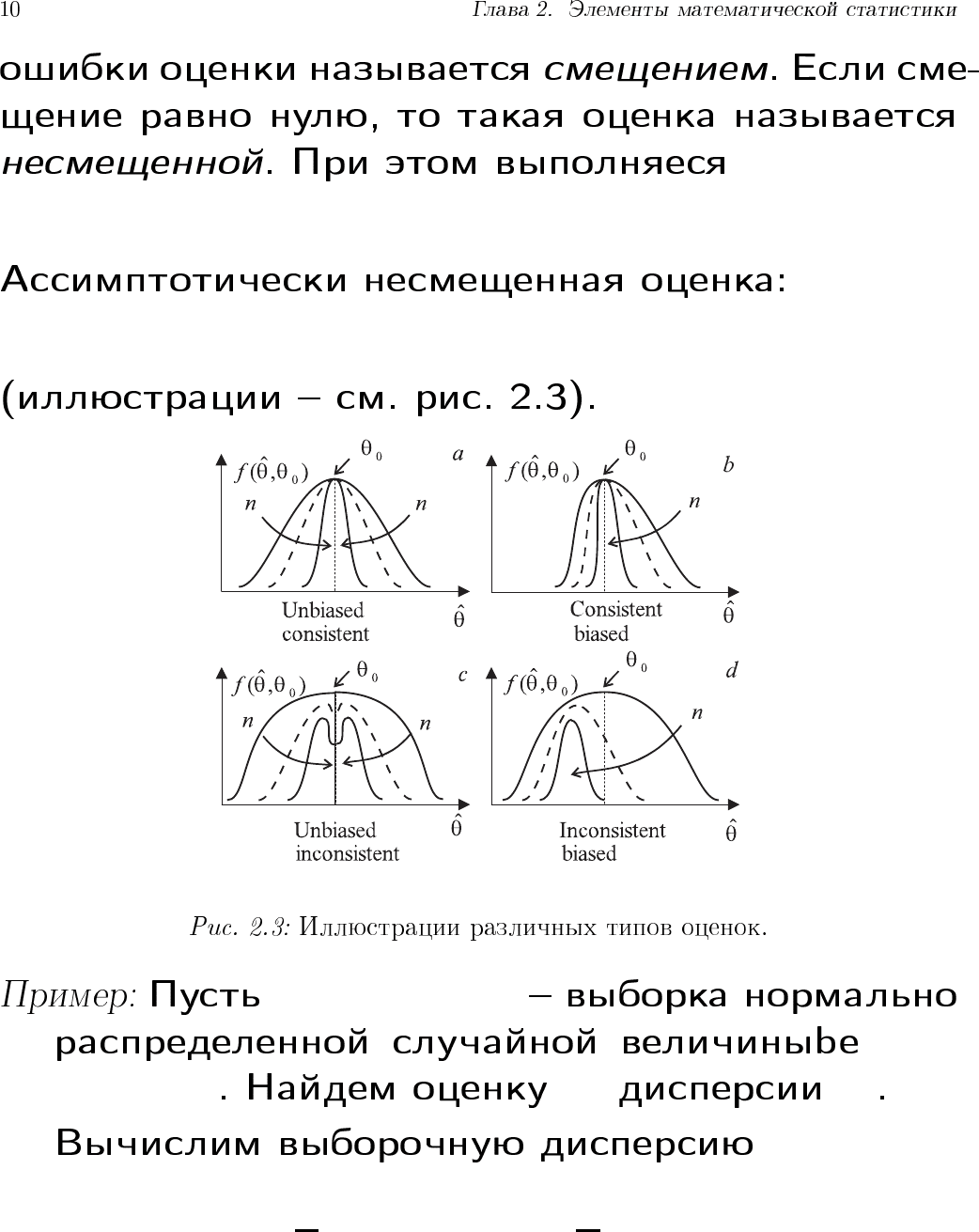
b
n
(
ˆ
θ) = M(
ˆ
θ
n
) − θ
0
= 0, M[
ˆ
θ] = θ
0
.
M(
ˆ
θ
n
)
n→∞
→ θ
0
(x
1
, x
2
, . . . , x
n
)
x
i
∈
N(m
ξ
, σ
2
ξ
)
ˆ
S
2
σ
2
s
2
=
1
n
n
X
i=1
(x
i
− ¯x)
2
=
1
n
n
X
i=1
x
2
i
− ¯x
2
.

M( s
2
) =
1
n
n
X
i=1
M( x
2
i
) − M(¯x
2
) =
1 −
1
n
σ
2
.
ˆ
S
2
=
n
n − 1
s
2
=
1
n − 1
n
X
i=1
(x
i
− ¯x)
2
,
M(
ˆ
S
2
) =
n
n − 1
M( s
2
) = σ
2
.
x
1
, x
2
, . . . , x
n
L(~x, θ) =
n
Y
i=1
f(x
i
, θ).
ˆ
θ =
ˆ
θ(x
1
, x
2
, . . . , x
n
)
L(~x, θ)
Z
. . .
Z
L(x
1
, x
2
, . . . , x
n
, θ)dx
1
, . . . , dx
n
= 1.

θ
Z
. . .
Z
∂L
∂θ
dx
1
, . . . , dx
n
= 0.
ˆ
θ
M
ˆ
θ = θ
Z
. . .
Z
ˆ
θLdx
1
, . . . , dx
n
= θ,
Z
. . .
Z
ˆ
θ(x
1
, . . . , x
n
)
∂L
∂θ
dx
1
, . . . , dx
n
= 1.
Z
. . .
Z
[
ˆ
θ − θ]
∂L(x
1
, . . . , x
n
, θ)
∂θ
dx
1
, . . . , dx
n
= 1
Z
. . .
Z
[
ˆ
θ − θ]
1
L
∂L
∂θ
Ldx
1
, . . . , dx
n
= 1.
M[(
ˆ
θ − θ)(
1
L
∂L
∂θ
)] = 1.
ˆ
θ − θ = V
1
L
∂L
∂θ
= W
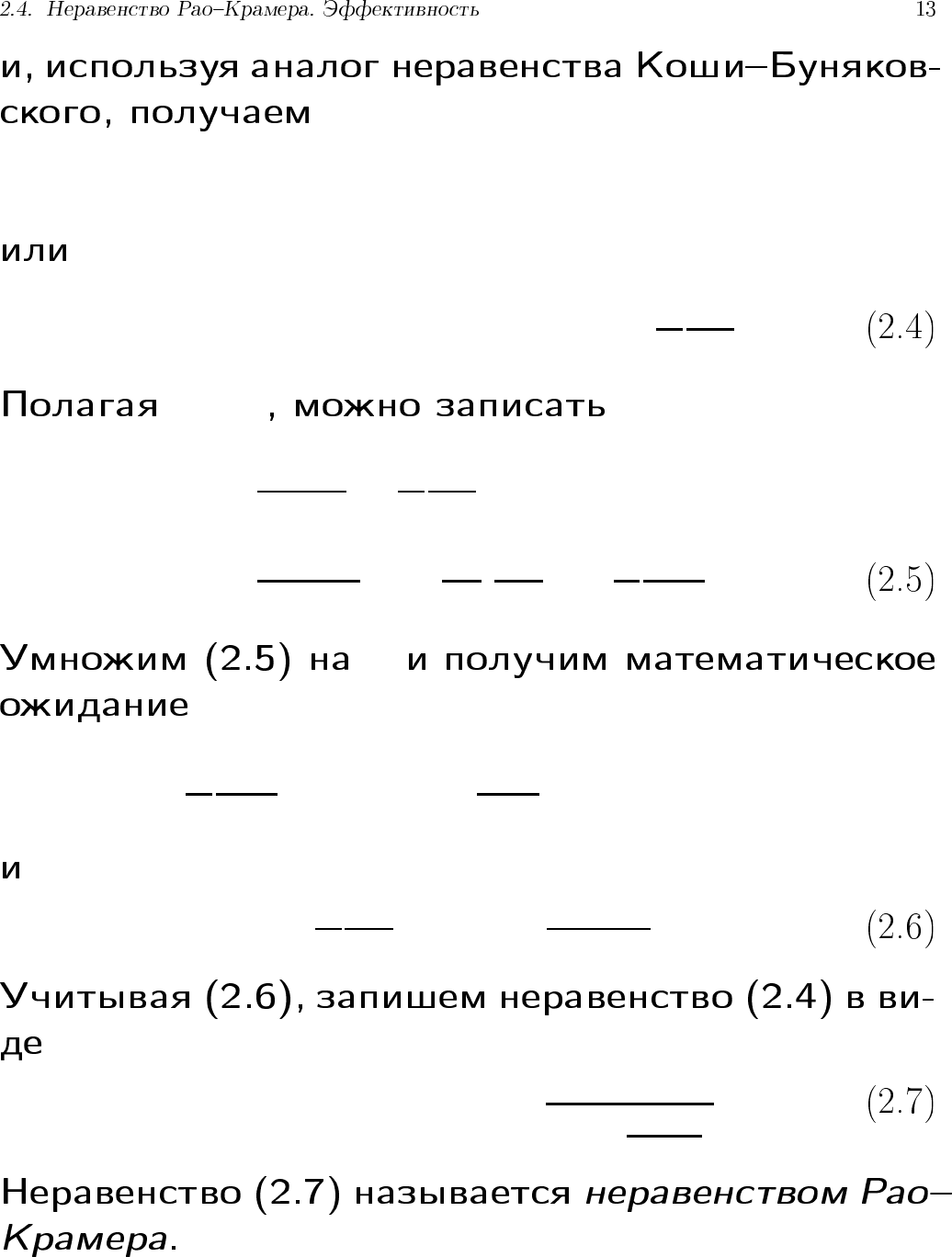
M( V
2
) · M(W
2
) ≥ [M(V · W )]
2
M( V
2
) · M(W
2
) ≥ 1, M(
ˆ
θ − θ)
2
· M[
1
L
∂L
∂θ
]
2
≥ 1.
L 6= 0
∂ ln L
∂θ
=
1
L
∂L
∂θ
,
∂
2
ln L
∂θ
2
= −
1
L
2
[
∂L
∂θ
]
2
+
1
L
∂
2
L
∂θ
2
.
L
M[
1
L
∂
2
L
∂θ
2
] =
Z
. . .
Z
∂
2
L
∂θ
2
dx
1
, . . . , dx
n
= 0
M[
1
L
∂L
∂θ
]
2
= −M[
∂
2
ln L
∂θ
2
].
D(
ˆ
θ)= M(
ˆ
θ − θ)
2
≥
1
M[−
∂
2
ln L
∂θ
2
]
.

M[−
∂
2
ln L
∂θ
2
] = M[
∂ ln L
∂θ
]
2
= I
(F )
(θ)
ˆ
θ
D(
ˆ
θ) ≥ (I
(F )
(θ))
−1
.
~
θ = (θ
1
, . . . , θ
s
)
D(
ˆ
~
θ) ≥ (I
(F )
(
~
θ))
−1
,
D
ss
′
= M[(
ˆ
θ
s
− θ
s
)(
ˆ
θ
s
′
− θ
s
′
)]
I
(F )
ss
′
= M[−
∂
2
ln L(~x,
~
θ)
∂θ
s
∂θ
s
′
] = M[
∂ ln L(~x,
~
θ)
∂θ
s
∂ ln L(~x,
~
θ)
∂θ
s
′
]
ˆ
θ
D(
ˆ
θ) = [I
(F )
(θ)]
−1
.

ˆ
θ(x
1
, . . . , x
n
)
θ
(x
1
, . . . , x
n
)
L(~x, θ)
L(~x, θ) = g(
ˆ
θ, θ)h(~x).


u
x
k
y
l
z
m
t
i
u(x
k
, y
l
, z
m
, t
i
), x
k
= k∆x, y
l
= l∆y, z
m
= m∆z, t
i
= i∆t.
~
θ = (θ
1
, . . . , θ
s
),
s
u
~
θ
f(
~
θ, x
k
, y
l
, z
m
, t
i
)
u(x
k
, y
l
, z
m
, t
i
) = f(x
k
, y
l
, z
m
, t
i
,
~
θ) + ε(x
k
, y
l
, z
m
, t
i
),
