Trent E.M., Wright P.K. Metal Cutting

Подождите немного. Документ загружается.

MANAGEMENT OF TECHNOLOGY 423

12. Furness, R., Proceedings of the CIRP International Workshop on Modeling of Machining

Operations, held in Atlanta, GA., Published by the University of Kentucky Lexington, KY,

40506-0108. (1998)

13. Taniguchi, N., Precision Engineering, 16, (1), 5 (1994)

14. Dornfeld, D.A., Lectures in Precision Engineering at the University of California Berkeley

(1999)

15. Smith, S., and Tlusty, J., Journal of Manufacturing Science and Engineering, 119, 664,

(1997)

16. Madden, A.P, and Moore, G., The Red Herring Magazine, 64 (April 1998)

17. Peterson, Science News, 152, 302 (November 8th., 1997)

18. Ayres, R.U. and Miller, S.M., Robotics: Applications and Social Implications, Ballinger

Press, Cambridge MA, (1983)

19. A Technology Roadmap for the Machine Tool Industry, The Association for Manufacturing

Technology. McLean, VA (1996).

20. 1997-98 Economic Handbook of the Machine Tool Industry, The Association for Manufac-

turing Technology. McLean, VA (1997).

21. Komanduri, R., Symposium on US Contributions to Machining and Grinding Research in

the 20th Century. Reprinted from Applied Mechanics Reviews Volume 46, Number 3,

March 1993 and available from the ASME Book Number AMR 126. (1993).

This Page Intentionally Left Blank

CHAPTER 14 EXERCISES FOR

STUDENTS

14.1 REVIEW QUESTIONS

14.1.1 Essential features of machining

1. Present in note form some practical and fundamental reasons why the machinability of an

alloy is difficult to assess. Make comparisons with the extrusion process.

2. Is it reasonable to describe pure copper as “easily machined”? Give reasons.

3. Define or describe in short, 3-4 line paragraphs, with equations or a diagram:

•i) Shear plane angle and its measurement.

•ii) Merchant’s force circle.

•iii) The force needed to achieve minimum energy.

•iv) The basic equation from the Rowe-Spick theory.

(14. 1)

4. Why is the shear plane angle an important point of focus in machining?

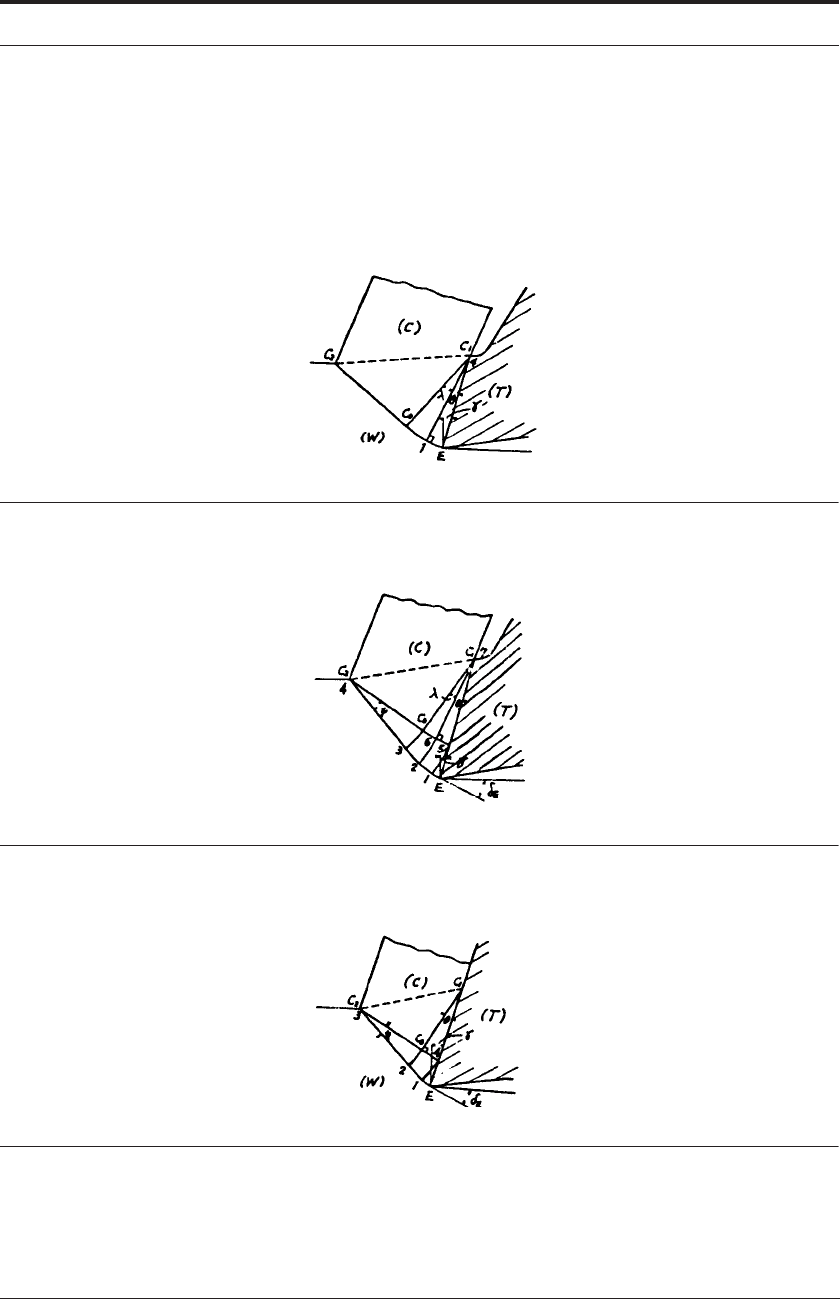
5a. Draw Merchant’s force circle and derive the theoretical expression for the shear plane angle:

develop the geometrical equations to show

(14. 2)

where = shear angle; = rake angle; λ = friction angle

dφ⁄ kus()

primary

βkus()

ondarysec

+0.==

φπ4⁄α2⁄λ2⁄–+=

φα

426 EXERCISES FOR STUDENTS

5b. Then develop a relationship for the theoretical cutting force. In this case do not present the

details of the differentiation method but explain the underlying principles and show the result.

5c. Comment on how well this analysis will fit experimental data.

6a. Draw the velocity triangle for the following single shear plane model of cutting.

FIGURE 14.1 Single shear plane with fan-shaped secondary shear zone (controlled contact tool).

6b. Draw the velocity triangle for this fan-shaped primary and secondary zone combined.

FIGURE 14.2 Fan-shaped zones in both primary and secondary.

6c. Draw the same field for an unrestricted tool face.

FIGURE 14.3 Unrestricted tool face.

7. Use the Rowe-Spick theory to calculate the shear plane angle for the following information

on free-machining steel.

•Speed = 100 m min

-1

REVIEW QUESTIONS 427

•Rake angle = 18°

•Feed rate = 0.285 mm/rev

•Contact length = 0.6 mm

• is part-sticking/part-sliding = 0.8.

8. A commercially pure copper machined with a 6° positive rake angle tool and a “quick stop”

section shows that full sticking friction occurs on the rake face. The undeformed chip thickness

is 0.30 mm per rev and the shear plane angle is 18°. What chip tool contact length is expected

from the Rowe Spick analysis?

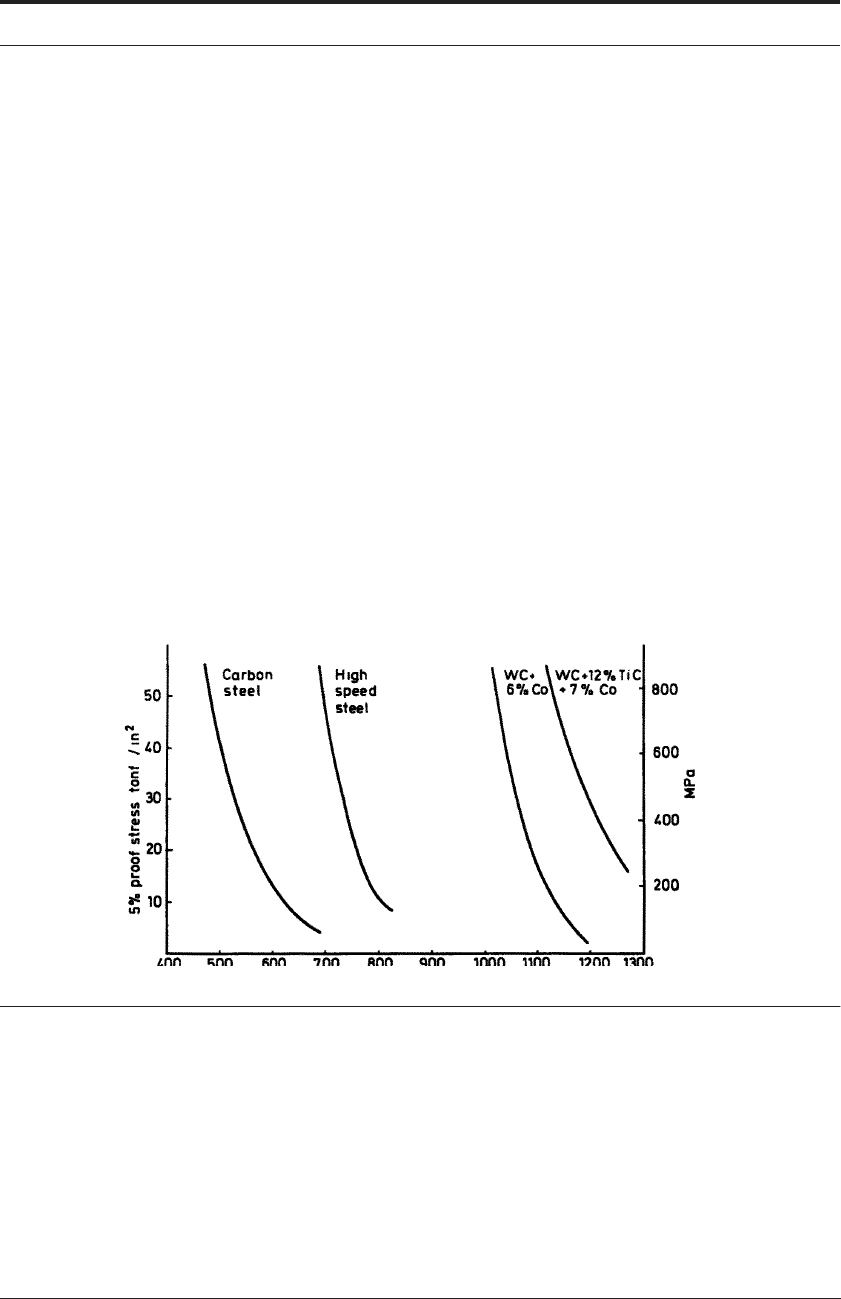
9. The following data was recorded when cutting a low alloy steel.

•Cutting force = 630 N

•Thrust force = 410 N

•Rake angle = 6°

•Chip width = 1.72 mm

•Contact length = 1.05 mm

•Temperature of tool edge = 775°C

Assume that the normal stress on the rake face is distributed evenly over the contact area and

then analyze the “ability to withstand wear by plastic deformation of the edge” for each of the

tool materials.

FIGURE 14.4 5% proof stress of tool materials

10. The figure below is a “quick stop” section taken from the machining of commercially pure

copper. The following data has been recorded:

•Cutting speed = 210 m min

-1

•Feed rate = 0.2 mm. (undeformed chip thickness)

•Shear plane angle = 14.81°

•Width of primary shear zone = 0.093 mm

428 EXERCISES FOR STUDENTS

Calculate

•i) The primary shear strain.

•ii) The primary shear strain rate.

•iii) The bulk chip speed, and show this in a velocity triangle.

FIGURE 14.5 Chip section of commercially pure copper

11. Categorize the chip forms shown in the figure below of “quick stop” sections of AISI 1045

steel. What range of cutting speed could be estimated for the four photographs? (Feed = con-

stant = 0.1 mm per rev, rake angle = + 6°).

FIGURE 14.6 Four chips from the same medium carbon iron

REVIEW QUESTIONS 429

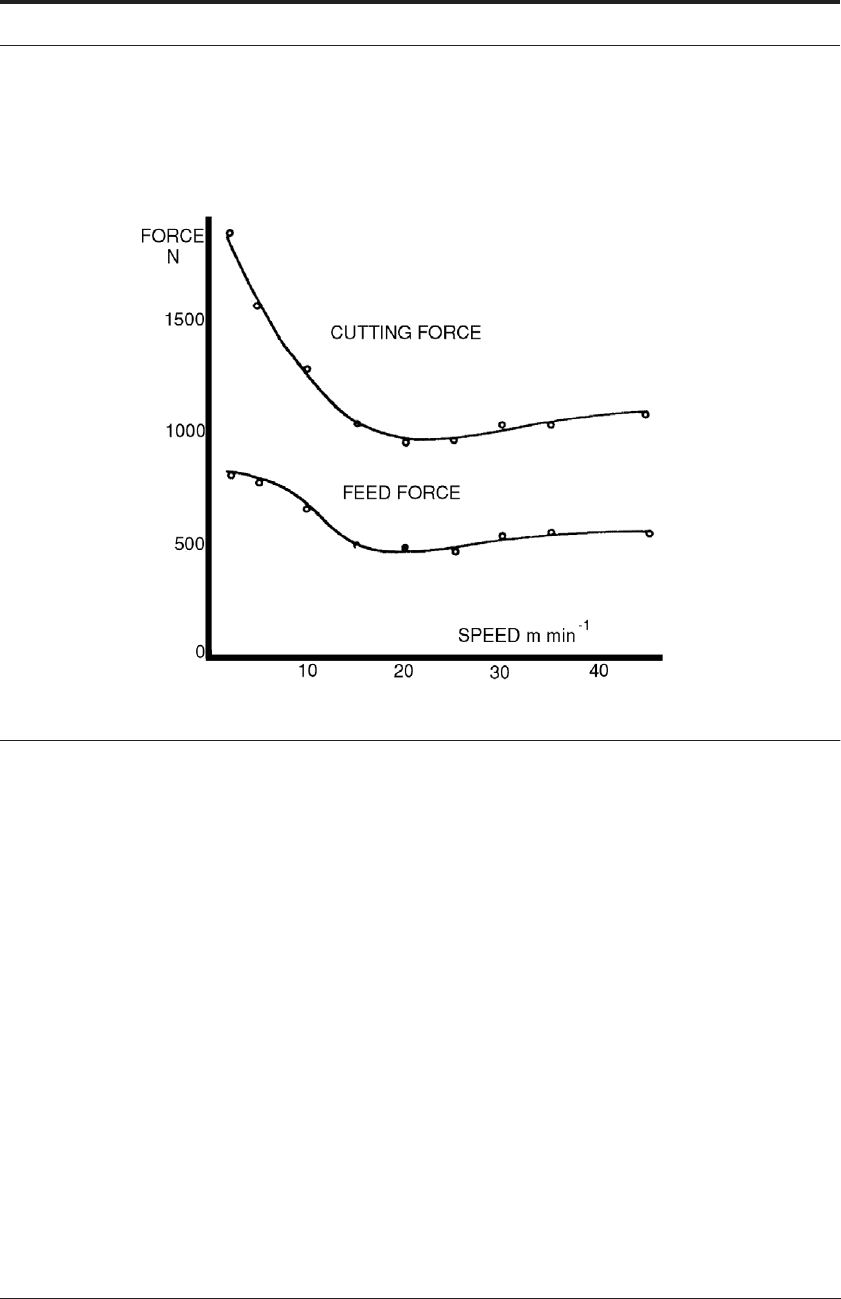
12. Calculate the range of power requirement for the results shown below when machining aus-

tenitic 13% manganese steel at a feed rate of 0.3 mm per rev.

FIGURE 14.7 Forces when machining austenitic 13% manganese steel

13. The following machining data for a bar of commercially pure copper should be used to cal-

culate:

a) The primary zone temperature

b) The temperature profile along the rake face to position 1.4mm

Undeformed Chip thickness = 0.2mm

Undeformed Chip width = 1.5mm

Rake angle = 6 degrees

Shear plane angle = 13 degrees

Main cutting force = 640 N

Thrust force = 315 N

Test bar initial temperature = 17 degrees C

Length of seizure content = 1.4 mm

Thickness of secondary zone = 0.07 mm

Cutting Speed = 100 m min

-1

Use typical room temperature values for the conductivity, density and specific heat of copper.

With these values and Figure 5.1, it should be found that approximately 52% of the heat goes

into the bar. Assume that plane strain conditions occur.

430 EXERCISES FOR STUDENTS

14.1.2 Supplementary questions on machining economics

14a. A batch of simple parts is made on a manual lathe. Verify that the cost per component, C,

may be given in terms of the {operator’s wage + overhead} = W, by:

(14. 3)

•WT

= “non-productive” costs, which vary depending on loading and fixturing

•WT

= actual costs of cutting metal

•WT

= the tool replacement cost shared by all the components machined. This cost is divided

up among all the components because each one uses up T

minutes of total tool life, T, and is

allocated of WT

•Using the same logic, all components use up their share of the tool cost, y.

14b. Which costs might be reduced by moving the job from a manual to a CNC machine? At

the same time, which costs might be increased? Factors such as batch size and part complexity

influence such decisions.

15. The right hand side of the above equation 14.3 can be re-formulated in terms of cutting

speed. The values of T

and T

are constants but the other times are speed dependent:

(14. 4)

is the Taylor equation that expresses the tool life T in terms of V.

(14. 5)

is an expression for the time to machine a round bar in a lathe where the length of the bar is (l),

its diameter (d), the feed rate is (f) and the cutting speed is V.

Units are peculiar to the standard industrial ways of expressing speed in meters per minute

and feed in terms of millimeters. Length and diameter are also in millimeters. To make all the

units compatible, the meters per minute are multiplied by 1000.

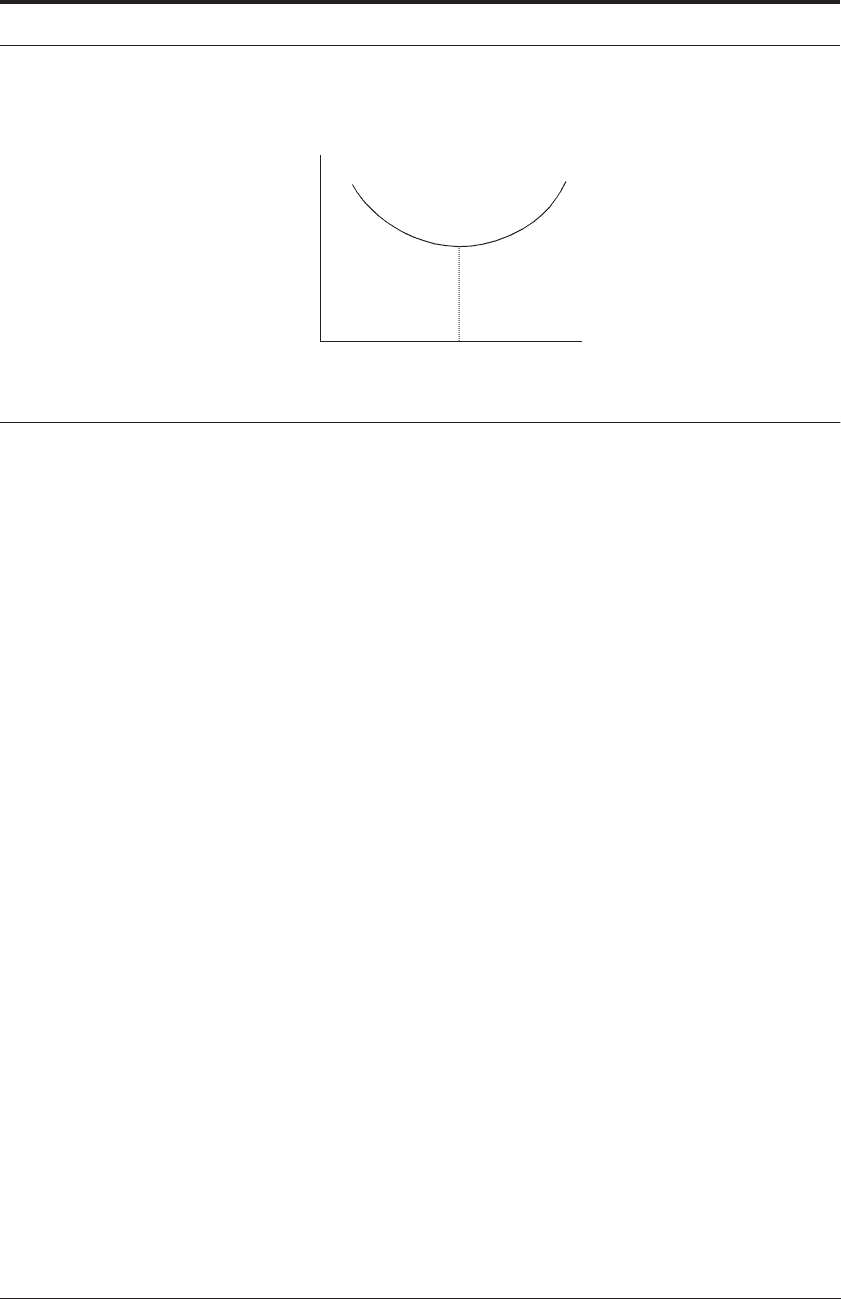
It is possible to calculate the optimum cost per component with respect to cutting speed.

Essentially, the idea is to differentiate equation 14.3 above with respect to V and find the mini-

mum in the curve below - Figure 14.8.

TOTAL

--------

+++=

-------

πdl()1000⁄ fV=

REVIEW QUESTIONS 431

FIGURE 14.8 Optimal cutting speed to minimize costs

On the left side of the figure, costs are too high - this is because the machine tool is “being

driven too slowly” and the machining time T

per component is too long. On the other hand, on

the right side, the costs are too high - this is because the machine tool is “being driven too fast”,

the tools wear out too fast and both T

and tool costs increase. {In a teaching situation one can

make the race-car analogy - too slow means too long around the track but too fast might mean

too many visits to the pits}.

The first step is to maximize the feed rate, f. This is done by choosing the surface finish (R

)

as the main criterion that controls part quality. This is given by the equation shown near the end

of Chapter 12, where (R) is the nose radius of the tool.

(14. 6)

The second step is to perform the differentiation of equation 14.3 using the sub-equations

14.4 and 14.5 to isolate the parameter V.

The expressions are rather cumbersome. Detailed analyses are presented in other machining

text books (such as Cook or Armarego and Brown - see Bibliography). Only the final equations

- usable in the next three examples - are given below. The value of T appearing in the following

equations is the value of tool life that will give minimum cost with variations in V. The cutting

speed, V, at the minimum cost is also shown in these equations and in the above figure as V

opt

At this optimum set of values, all the variable parameters (f, V, and T, etc) are denoted with a

superscripted star (*).

The third step is to make note of some minor additions to the procedure.

•First, the Taylor equations can also be prepared in terms of feed rate. However, increases in

feed rate are “less damaging” to the tool life than increases in speed - thus a value of n

also

appears which is the exponent that is obtained from tool life testing leading to plots of (T vs.

f). The value of n

first appears in the third equation below - equation 14.9.

•Second, since the Taylor equations are now a function of both V and f, the constant (C) is

replaced by the constant (K), which combines both the feed and speed constants. This is also

shown in equation 14.9.

opt

Costs

0.0321 f

R⁄()=

432 EXERCISES FOR STUDENTS

•Third, to account for the variables in the main equation 14.3 that are not directly related to

change in speed, another constant (R) is formed that combines the tool cost, y, {operator +

machine cost} = W, and the tool replacement time, T

. All times are measured in minutes,

and all costs in cents. As a specific example - in the first case study - (R = 3 + 70/11.67). This

is because there are 4 edges in the insert (280/4 cents), and the operator + machine costs are

700/60 cents per minute.

(14. 7)

(14. 8)

(14. 9)

(14. 10)

- or - (14. 11)

In summary, the above equations relate the optimized tool life, T*, the recommended cutting

speed, V*, and the recommended feed rate, f*, to get the minimum in the parabolic graph

shown earlier. Equation 14.5 gives T

15a. The tool life relationship for a single pass turning operation on 18-8 stainless steel with a

WC-TiC-Co tool is:

(14. 12)

where V is the cutting speed in m min

-1

and f is the feed rate in mm per rev. The “throwaway”

insert costs $2.80 but offers 4 cutting edges; the machining plus overhead costs are $7.00 per

hour; the time taken to change a cutting edge is 3 mins., and the non-productive time per com-

ponent is 30 seconds. The component diameter is 25 mm and its length is 100 mm.

If the feed rate must not exceed f* = 0.3 mm per rev to achieve a satisfactory surface finish,

calculate:

yW()⁄()+=

---1–

⎝⎠

⎛⎞

()

1n/–

f()

-----–

()

-----

----------------------=

1n–

------------+

⎝⎠

⎜⎟

⎛⎞

⎝

⎠

⎜

⎛

⎞

------+

⎝⎠

⎜⎟

⎛⎞

⎝⎠

⎜⎟

⎛⎞

⎝⎠

⎜⎟

⎛⎞

mins()

7.5 10

2.15

----------------------=