Trent E.M., Wright P.K. Metal Cutting

Подождите немного. Документ загружается.

FINITE ELEMENT ANALYSIS BASED MODELS 383

triangles, rectangles and similar shapes - called subregions or elements - give a piecewise

approximation to the continuum equations. Finite element analysis reduces a continuum prob-

lem with infinite variations to a discretized problem with very large number but a finite number

of unknowns. The roots of the FEA method are often traced to the Courant Institute in New

York.

The solution region is first divided into elements. Then the unknown field variable (in this par-

ticular case T) is expressed in terms of an assumed approximating function within each element.

The approximating function - called an interpolation function - is defined in terms of the values

of the field variable at specified corners of the mesh elements - these are called the nodes or

nodal points. The nodal values of the field variable, and the interpolation functions for the ele-

ments, completely define the behavior of the field variable within the elements. For the finite

element representation of any problem, the nodal values of the field variable become the new

unknowns. Once these unknowns are found, the interpolation function defines the field variable

throughout the assembly of elements.

FIGURE 12.8 Continuum approach on the left vs. discretized FEA approach on the right

384 MODELING OF METAL CUTTING

12.5.2 Developing the analysis

(a) Discretize the continuum

: As reviewed by Black

the first step is to divide the solution

region into the elements shown on the right of Figure 12.8. A variety of element shapes are used

in the same solution region. The number and type of elements to be used in any given problem

are matters of judgement, experience and trial and error. For example, the authors and colleagues

have studied other metal-processing problems that involve high friction at a tool/work interface.

It was critical to use a very fine mesh at that interface to obtain results in which theory and

experiment matched each other.

(b) Select the interpolation function(s): The next step is to assign the corner nodes to each ele-

ment and then choose the type of interpolation function that represent the variations of the field

variable over the elements. Often, although not always, polynomials are selected as interpola-

tion functions for the field variable because they are easy to integrate and differentiate. The

degree of the polynomial chosen, depends on the number of nodes assigned to the element, the

nature and number of unknowns at each node, and certain continuity requirements.

express the properties of the individual elements. Four possible schemes are reviewed below: i)

the direct approach, ii) the variational approach, iii) the weighted residual approach, iv) the

energy balance approach.

(d) Assemble the element properties to obtain the system equations: To find the properties of the

overall system, the matrix equation for each element must be integrated with all other matrix

equations in order to finally express the behavior of the solution region or system. The assembly

procedure relies on the fact that, at any node where elements are interconnected, the value of the

field variable must be the same for each element sharing that node. Finally, before the system

equations are ready for solution on the computer, they must incorporate the physics of the

boundary conditions of the problem. For metal cutting they will include friction at the interface

and the temperature conditions at the boundaries of the workpiece, toolholder and free edge of

the chip.

(e) Solve the system equations: The assembly process of the preceding step gives a very large

set of simultaneous equations that can be solved on a computer to obtain the unknown nodal val-

ues of the field variable - in this discussion the temperature T.

12.5.3 Approaches to the finite element analysis (FEA)

The four different approaches to formulating and calculating the properties of individual ele-

ments include:

(a) Direct approach: Structural analysis in civil engineering is the origin of the direct approach

(equation 12.20). This direct approach is based on a direct stiffness method of the structure.

(b) Variational approach: Element properties can also be determined by the more versatile vari-

ational approach. The variational approach relies on the calculus of variations and involves

extremizing the functions. In solid mechanics, the functional turns out to be potential energy, the

complementary potential energy, or a derivative of these.

the weighted residuals approach. It begins with the governing equations of the problem and pro-

ceeds without relying on a functional or a variational statement. This allows a finite element

analysis to be used on problems where no functional is available.

FINITE ELEMENT ANALYSIS BASED MODELS 385

(d) Energy balance approach: This approach relies on the balance of thermal and/or mechani-

cal energy of a system. The energy balance approach requires no variational statement and

hence further broadens the possible applications.

FIGURE 12.9 Overview of finite element solution procedure (Courtesy J.T. Black)

12.5.4 Application of FEA to the specific problem of machining

How do the matrix equations shown near the bottom of Figure 12.9 get solved in a situation

where the tool and work material are in relative motion? As summarized by Athavale and Stren-

kowski,

the two basic approaches are the Lagrangian and the Eulerian formulations, together

with an arbitrary Lagrangian-Eulerian formulation.

386 MODELING OF METAL CUTTING

12.5.4.1 Lagrangian formulation

In a Lagrangian formulation, the mesh is “attached to the workpiece”. In a virtual sense it

resembles the experiments in which researchers etch a photogrid onto the workpiece and then

study its deformation during cutting. The tool or workpiece is advanced through predefined dis-

placement increments, and the finite element solution is obtained. The displacement increment is

a function of the time step in explicit solution methods.

32,33

This can be related to the material

removal rate during cutting. By contrast, in an implicit solution,

34-37

the time step has no physi-

cal significance. In the various papers in the literature, different material models are used: they

include i) elastic-plastic, ii) only plastic, iii) viscoplastic, and iv) additive

as well as

multiplicative

decomposition of elastic and plastic strains.

From a civil engineering (structural) viewpoint, the application of finite element analysis for

stress analysis leads to a system equation for the nodal displacement vector

{u} of the system as

follows:

(12. 20)

where

[K] = the global stiffness matrix and

{R} = the load vector which include all its applied loads.

The solution of the system of the equation yields the nodal displacement vector {u} from

which the element strains and hence stresses can be calculated.

By contrast from a metal cutting viewpoint, the assumptions used in the above equation 12.20,

namely small displacement linear analysis and constant material properties, are no longer valid.

In the updated Lagrangian formulation, because the elements move with the workpiece, they

experience both large plastic deformation and rigid body motion. Under such circumstances, the

larger deformations, and the changing material properties due to stress and strain in the material,

need to be considered. The global stiffness matrix [K] is no longer constant. The stiffness matrix

is dependent on the current geometry and the stress history imposed by the loading sequence.

Since the governing equations are now nonlinear, the system must be solved iteratively on the

computer.

The advantage of the updated Lagrangian formulation is that the tool can be simulated from

the start of cutting to a steady-state. One of the disadvantages, however, is that the model

requires large computational times to reach steady-state conditions. In addition, a material fail-

ure and “parting-line or separation” mechanism has to be provided to allow the chip to sepa-

rate from the workpiece.

In the Lagrangian formulation, this “parting-line” or “separation” mechanism of the chip from

the parent workpiece material ahead of the tool tip remains a significant and controversial issue

for researchers. Nodes on this line are separated, and the line “unzipped”, when the tool tip is

sufficiently close, or when a certain level of plastic strain is attained. Various schemes have been

employed as criteria to part the chip: they include effective strain,

geometric distortion,

and

crack generation and propagation.

To implement the chip parting line, several algorithms have

been used: the slide-line,

node/element birth and death,

and remeshing.

K[]u{} R{}=

FINITE ELEMENT ANALYSIS BASED MODELS 387

Obviously, this “unzipping” approach makes assumptions both on the location and stress level

of the “failure”, namely the cutting of the material. Sekhon and Chenot

and Marusich and

Ortiz,

by contrast, have investigated mesh adaptivity and remeshing to allow for an arbitrary

surface of separation. This approach is much more desirable because it more accurately models

the cutting process. However, it is a time-consuming task to numerically perform the remeshing

and mesh adaptivity and it is still dependent on the material model to correctly describe the

“parting-line failure” in the workpiece just ahead of, or at the very tool tip.

A related problem in a Lagrangian formulation is the computational instability due to the large

distortion of some elements. This problem may eventually cause unrealistic results or premature

termination of the analysis. Severe element distortion also results in a degradation of the accu-

racy. To address this issue it is useful to redefine the mesh system periodically - a process called

rezoning. The rezoning involves the assignment of a new mesh through interpolation. The capa-

bility of rezoning has been included in many finite element codes for large displacement, large

strain, plastic deformations.

12.5.4.2 Eulerian formulation

In the Eulerian formulation, the workpiece material is assumed to flow through a meshed con-

trol volume - the cutting zone. This Eulerian viewpoint focuses attention on a particular point in

space and then examines the phenomena occurring there.

The cutting process is treated as a large deformation process involving a viscoplastic material.

It is assumed that elastic effects are negligible. Therefore, the constitutive law becomes a vis-

cous flow equation relating flow stress to the instantaneous strain rates.

(12. 21)

where

= the viscosity which is dependent on the strain rate

The global matrix for all elements in the chip and workpiece is found by summing the contri-

bution for each element. This results in the following equation:

(12. 22)

where

[K] = the global stiffness matrix

{U} = the nodal velocities

{P} = the vector of all applied nodal loads

There are three iterative cycles that are performed during this simulation:

(1) The first involves solving the viscoplastic equation for velocity and strain-rate distribution

in the chip and workpiece. An estimate of the strain-rate is initially used to calculate the viscos-

ity at ambient temperature conditions. After each iteration, the strain-rate is compared to the ini-

tial value. The iterations are continued until the initial and calculated strain-rate converge.

σ{} C μ(){}]ε

{}[=

K[]U{} P{}=

388 MODELING OF METAL CUTTING

(2) Once the velocities have been determined, the temperature is calculated. Because, in gen-

eral, the thermal properties of both the workpiece and tool will depend on the temperature, an

iterative solution is again required until the temperatures converge.

(3) The final step consists of updating the chip geometry to ensure that the computed velocities

on the chip surfaces are parallel to the free surfaces. As Athavale and Strenkowski

point out,

one disadvantage of the Eulerian formulation is that the boundaries of the chip free surface i)

need to be known in advance and ii) also need to be adjusted iteratively during the simulation.

This issue can be addressed in an updated Eulerian approach as follows. At the end of each

iteration step the calculated velocity field is integrated. Then, the displacement obtained can be

used to create a new geometry, which defines the next Eulerian step. During such calculations,

the free surface of the chip, and the chip shape, must be determined explicitly. Also, the work-

piece velocities must be determined explicitly. The incoming bulk workpiece velocity must

obviously be tangential to the element sides that represent the external physical boundaries of

the free surface of the workpiece and newly forming chip. Similarly, the two boundaries of the

formed chip - one along the rake face and the other opposite on the chip’s free surface - must be

repositioned iteratively. The repositioning of these two chip boundaries may be independent

dependent.

Also note that for the Eulerian formulation, the strains have to be computed from

the strain-rates by integrating along stream lines. Thus the basic method is not applicable to a

discontinuous workpiece that the tool would cut in an interrupted fashion. Space-time Eulerian

formulations

are being developed for discontinuous workpieces, discontinuous chips and seg-

mented chips and these will see further uses in the future.

12.5.4.3 Summary

Despite these challenges, the main advantage of the Eulerian formation is that it eliminates the

need for an explicit material failure or separation criterion. For Eulerian models, the chip parting

criteria occurs at the stagnation point at the tool tip. And this is obtained from the velocity distri-

bution. Further, physical separation of the chip and workpiece nodes are not required, since the

mesh is not attached to the workpiece surface.

12.5.5 Brief historical perspective of FEA use in metal cutting research

The reader is first referred to a comprehensive review by Chen and Black.

This contains most

of the significant citations up to the early 1990s. Second, the collection of papers edited by Jawa-

hir, Balaji and Stevenson

contains contributions from many of today’s investigators in the FEA

area.

The earliest papers appeared in 1973. Klamecki

analyzed the stress state transition from

plane stress at the workpiece surface to plane strain in the central region of the shear zone, and

Tay et al

27, 48-50

presented a two-dimensional model of the temperature distribution generated

during orthogonal machining. It used the following two-dimensional energy equation,

for the

heat conduction and convection:

(12. 23)k

∂

∂x

---------

∂

∂y

---------+

⎝⎠

⎜⎟

⎛⎞

ρC

∂T

∂x

------

∂T

∂y

------

⎝⎠

⎛⎞

– q

+0=

FINITE ELEMENT ANALYSIS BASED MODELS 389

where k

is the thermal conductivity, is the density, is the specific heat, T is the tempera-

ture and is the volumetric heat generation rate.

The following boundary conditions apply:

T = T

on a surface S

where T is defined,

on a surface S

where q is defined.

(T - T ) on a surface S

where is h is defined.

By the late 1970s, Tay, Stevenson, de Vahl Davis and Oxley

49,50

had successfully adapted the

analysis to avoid the need for a flow field as input, partly based on Stevenson and Oxley’s ear-

lier work.

Also, a basic mesh for a given tool geometry was automatically adjusted for shear

angle and contact length over wide range.

Stevenson, Wright and Chow

also used the tool etching method described in Chapter 5 to

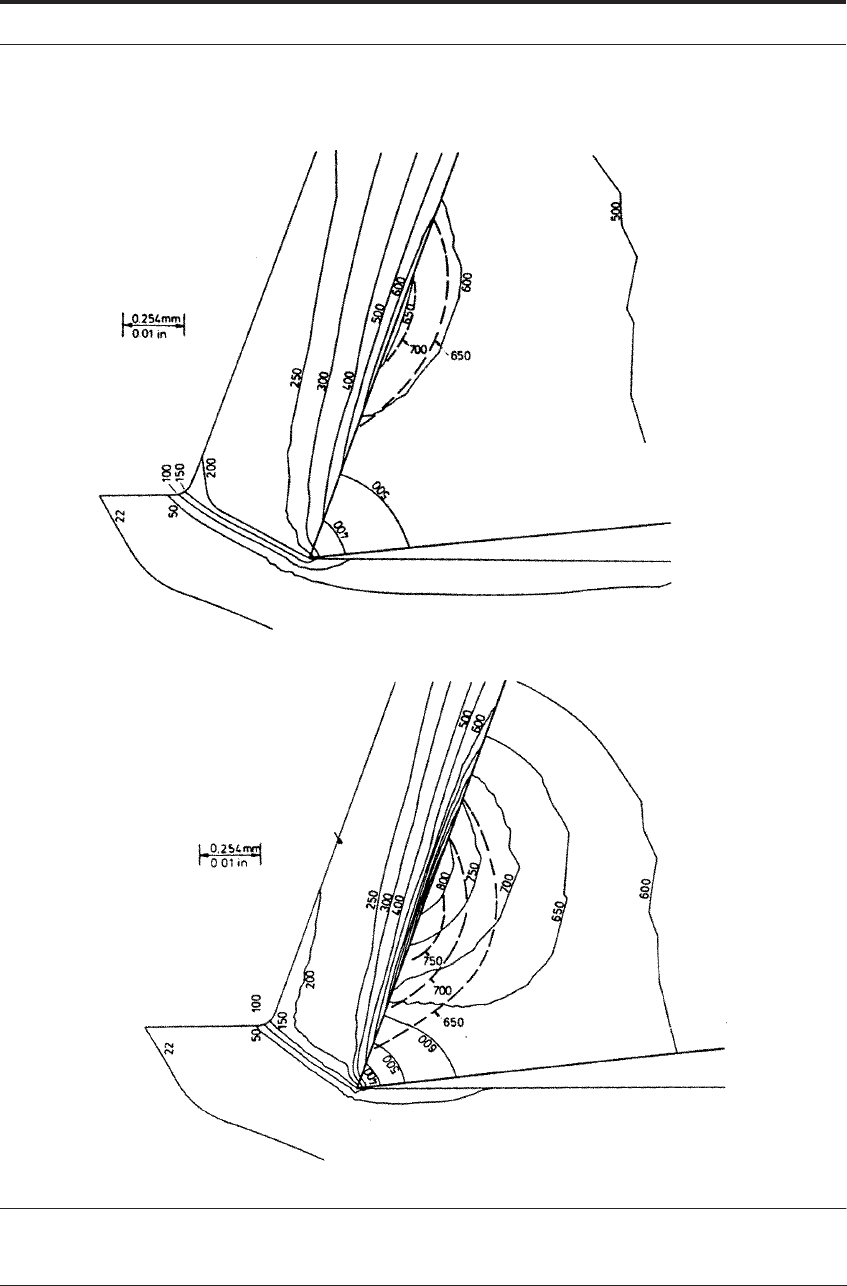
verify the FEA predictions. Figure 12.10 shows very good agreement, with a discrepancy

between experiment and calculation of only about 50°C, although in this case the calculation

gives the higher temperatures. Also, the isothermals of the calculation in the second case are dis-

placed along the rake face from those of the experiment, suggesting an error in the measurement

of the contact length used as input to the calculation.

Such an error could also have arisen from the formation of the crater. The contact length scar

which was measured on the tool may have resulted from the early period of the cut before the

crater formed. Formation of the crater would promote chip curl and gradually reduce contact

length as the cut continued.

Also in the late 1970s, Muraka, Barrow and Hindjuka

published a finite element analysis for

calculating the temperature distributions in orthogonal machining. They used the same govern-

ing equation and boundary conditions as Tay et al., and obtained the solution by using the Galer-

kin method.

The effects of coolant on temperature distribution in metal cutting were then studied both

experimentally and theoretically by Childs, Maekawa and Maulik,

using an analysis similar to

that of Tay et al. An interesting conclusion reached, compatible with the findings in Chapter 10,

was that the effect of coolant was least on the rake face, greater on the flank face and greatest on

the tool and tool holder.

In related work, Maekawa, Nakano and Kitagawa

found that the use of a high-thermal-con-

ductivity tool such as diamond, was more effective in reducing the rake temperature than the use

of a coolant. This tendency became more obvious when a low-thermal-conductivity material

such as a titanium alloy was machined.

ρ C

∂T

∂n

------

– q=

∂T

∂n

------

∞

390 MODELING OF METAL CUTTING

FIGURE 12.10 Experimental results from the tool etching method (dashed lines) in Chapter 5 and the

corresponding FEA predictions Cutting speeds:61 m min

-1

and 106 m min

-1

FINITE ELEMENT ANALYSIS BASED MODELS 391

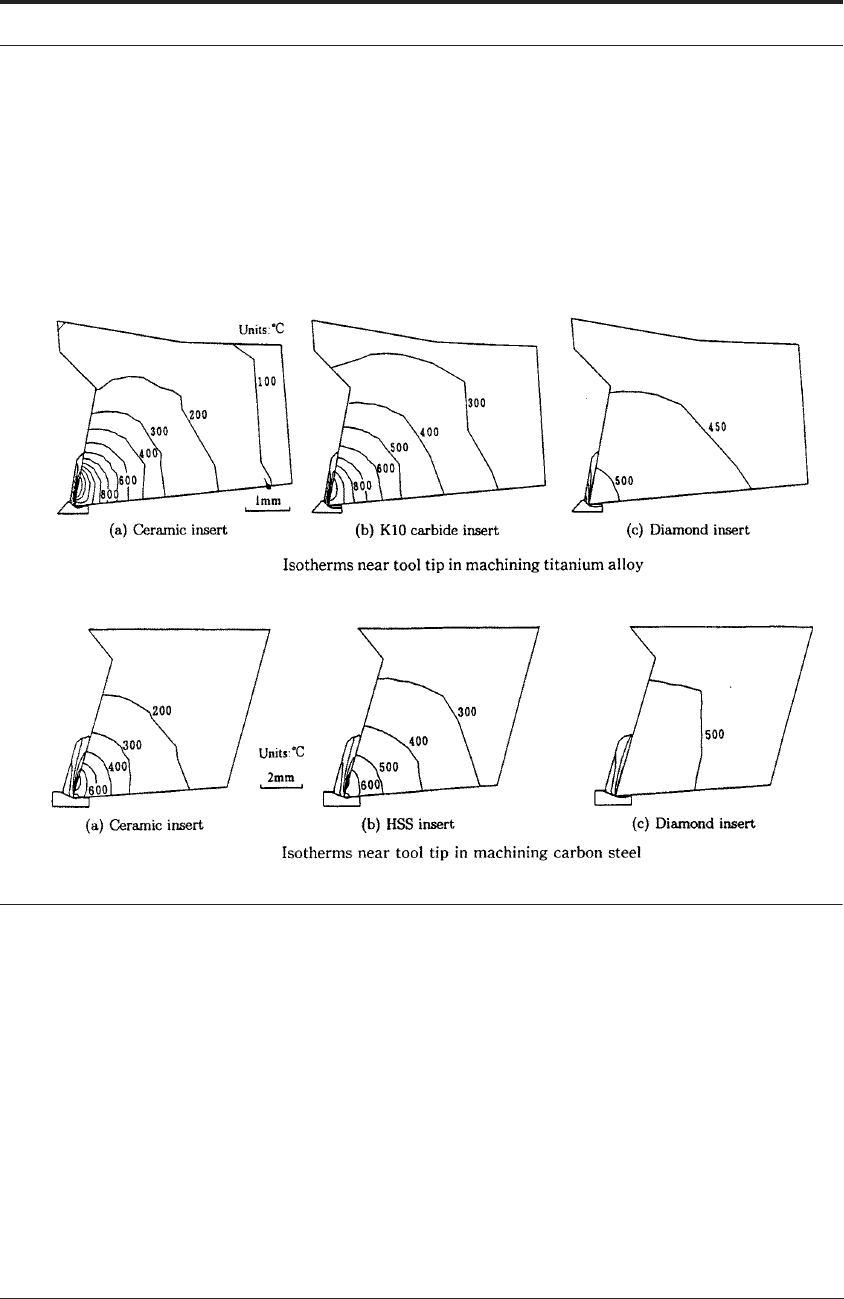
For example, Figure 12.11a shows the steady cutting temperature when machining the tita-

nium alloy in air using a) ceramic, b) carbide and c) diamond tools. Figure 12.11b shows a sim-

ilar result for machining medium-carbon steel. The intervals of isotherms in both figures are

100°C. The cutting temperature for the titanium alloy is higher for every tool type, even though

a low cutting speed and feed was set as compared to the steel machining. An interesting result is

that the edge temperature for the ceramic tool, whose thermal conductivity is the lowest, mark-

edly increases to as high as 1300°C.

FIGURE 12.11 Maekawa et al.’s calculated isotherms near tool tip a) above: when machining titanium

alloy b) below when machining medium-carbon steel

12.5.5.1 Lagrangian examples

Following the early FEA-machining papers of the 1970s, both Lagrangian and Eulerian

approaches have been developed over the last twenty years.

In 1991, for example, Komvopoulos and Erpenbeck

used the general purpose code

ABAQUS and an updated Lagrangian formulation. A distance criterion was used as the chip

separation criterion. They investigated two possible constitutive deformation laws: i) elastic-

perfectly plastic (EPP) and ii) elastic-plastic with isotropic strain hardening and strain rate sensi-

tivity (EPSHR). Unworn and worn (cratered) tools with strongly adherent built-up edges were

used for comparison. A total of five finite element simulations with different material models,

different friction coefficient values and different tool geometries were studied to find their

effects on the cutting process. Coulomb’s law was used for the modeling of the tool-chip inter-

392 MODELING OF METAL CUTTING

face friction - the reviews of the seizure conditions in Chapters 4 through 9 indicate that their

results could still be re-run with different boundary conditions and some new insights will

emerge.

Lin and Lin

also developed a thermo-elastic-plastic finite element model based on the

updated Lagrangian formation and the Prandtl-Reuss flow rule. A strain energy density was used

as the chip separation criterion. This is a material constant representing the energy absorption

capability, and was determined from a uniaxial tensile test.

12.5.5.2 Eulerian examples

In 1990, Strenkowski and Moon

employed an improved Eulerian model. In this modified

version, a separate procedure was used to predict the chip geometry and chip/tool contact length.

The chip geometry was predicted by requiring that material velocity normal to a free surface be

zero. This method was originally proposed by Zienkiewicz et al.

Once the chip geometry was

determined, the contact length was predicted by checking the normal stress at every node along

the tool-chip interface. A positive normal stress at any node along the interface meant that this

particular node had been released from the tool/chip interface. The predicted contact length was

then determined and used to modify the thermal conduction path between the chip and the tool.

Also, Strenkowski and Hiatt

coupled the stresses resulting from the improved Eulerian

model with a fracture mechanics model proposed by Broek.

It allowed the prediction of the

ductile regime in a single point diamond turning operation on a brittle material. In further work,

Strenkowski, Larson and Chern

coupled the temperatures resulting from the improved Eule-

rian model with a tool-wear by diffusion model. In this work, thermal infinite elements were

used for the flow zone in secondary shear. The infinite element

differs from the standard finite

element because one of its edges is made to extend to infinity - such an element geometry is use-

ful for unbounded field problems. Given the nature of the flow zone (e.g. a thin zone where

shear strains are between 20 and 50 - see Chapters 4 and 5) the use of an element which is very

long and thin has great intuitive appeal. Once Strenkowski et al. had calculated the temperature

distributions in such a way, the depth of the diffusion wear along the tool rake face was then

determined from the diffusion coefficients.

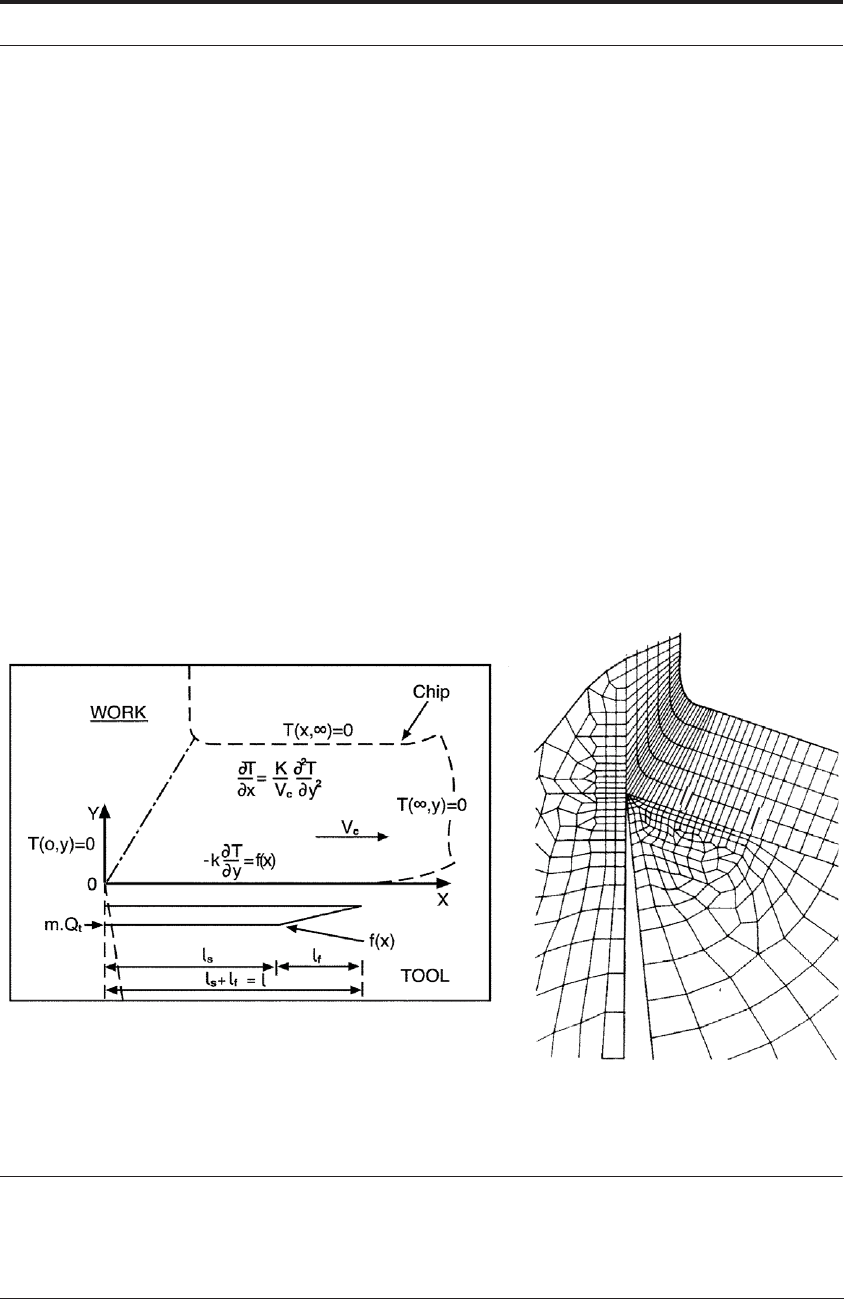
12.5.6 Case study I: modeling chip-breaker grooves

Jawahir and colleagues developed an Eulerian formulation that followed the Hu-Washizu vari-

ational principle.

The global stiffness matrix was based on equation 12.22 in the earlier sec-

tion, and similarly the constitutive equation was:

(12. 24)

where is the effective stress, is the strain-rate and temperature dependent viscosity

and is the strain-rate. The thermal effects were developed from the same 2-D

equation as Tay et al’s.

The model also included the chip-groove on the tool rakeface. The boundary conditions used

for the deformation analysis and the thermal analysis are shown in Figure 12.12.

First, the normal component of the velocity at the tool-chip interface is set to be zero.

Second, a frictional, tangential stress is prescribed at the tool-chip interface and the groove back-

wall. In the “controlled contact” or land region - see Figure 4.11 - it is assumed that the chip is

σμε

σμ

μμσε

T ε,,,()=

()