Тимофеев В.Н. (ред.) Применение магнитогидродинамических устройств в металлургии

Подождите немного. Документ загружается.

284

Рис. 1.6.11 – Источник питания ВГТ2 – 25/66

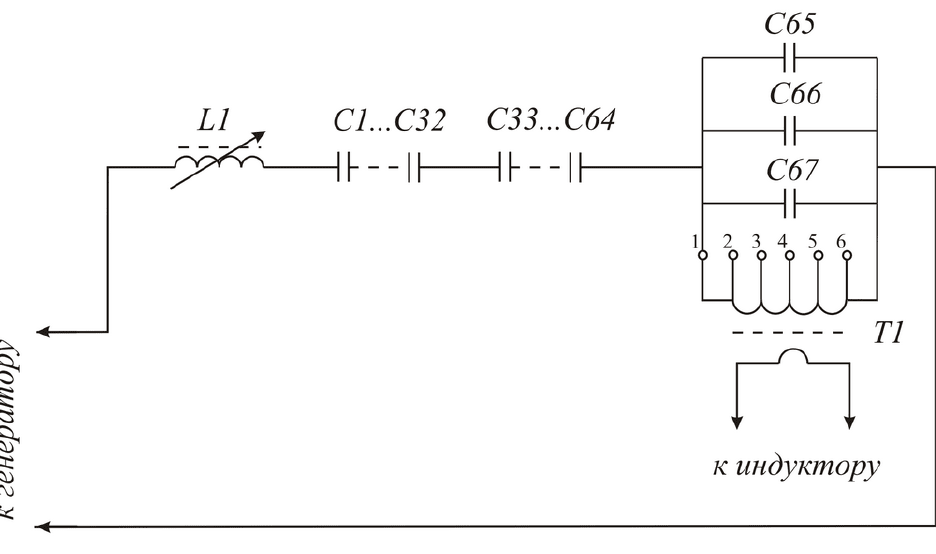
Электрическая схема согласования параметров индуктора с

параметрами источника питания представлена на рис. 1.6.12. Схема состоит

из водоохлаждаемого дросселя L1, последовательной батареи конденсаторов

К78-2-1000В (C1 - C64), общей емкостью 150.9 нФ, параллельной батареи

конденсаторов К78-21А-500В (С65 - С67), общей емкостью 4.1 мкФ, и

согласующего трансформатора ТС1 (Т1) с шестью отпайками для

регулирования напряжения на нагрузке. Ввиду

того, что в параллельном

контуре протекают большие токи, порядка 1–1,5 кА проводящие элементы

охлаждаются водой.

285

Рис. 1.6.12 – Электрическая схема контура согласования генератора и трансформатора

Для надежной работы генератора обеспечена гальваническая развязка

индуктора и генератора не менее чем на 1,5 кВ действующего значения

напряжения, которая осуществлена с помощью трансформатора.

Настроечные работы согласования индуктора с генератором

осуществляются при питании силовых цепей генератора от внешнего

источника постоянного тока с напряжением на выходе

В 60

, подключаемым

к гнездам на лицевой панели генератора со строгим соблюдением

полярности. Нагрузочная цепь подключается к выходу генератора, а во все

водоохлаждаемые элементы подается вода. Включение нагрева

осуществляется при максимальной частоте. Затем, понижая частоту,

фиксируется изменение тока на выходе генератора и напряжения на

параллельном контуре. Изменением частоты и параметров контура

необходимо

добиться, чтобы максимальный ток при 60 В составлял не более

4 А, а напряжение на параллельном контуре не более 40 В. Если эти условия

выполнены, можно переходить на полное напряжение 600 В.

Для измерения электрических параметров в режиме настройки и

работы использован милливольтметр В3-38, трансформатор тока

высокочастотный и встроенные амперметр и вольтметр преобразователя

частоты

и внешнего источника постоянного тока.

286

1.6.4 Технологические параметры процесса литья

К основным параметрам процесса литья относятся скорость,

температура металла, напряжение на индукторе и интенсивность охлаждения

слитка.

Скорость литья влияет на качество слитка, а так же на технико-

экономические показатели процесса в целом. Наибольшее влияние скорость

литья оказывает на производительность процесса, определяемого как

количество массы металла, отлитого в единицу времени. При

этом скорость

литья должна быть меньше, чем критическая, при которой слиток

разрушается.

Величина критической скорости литья слитков зависит от химического

состава отливаемого сплава, формы и размера поперечного сечения слитка.

Чем больше расплав содержит легирующих элементов, тем ниже его

пластичность, тем в большей мере приходится ограничивать скорость литья

[8, 9]. В ряде случаев

при выборе скорости литья на первый план выступают

качественные характеристики: высота, плотность, равномерность структуры

и механические свойства по сечению слитка.

Температура литья влияет на форму, величину зерна и внутреннее

строение слитка. С повышением температуры литья возрастает склонность к

столбчатой кристаллизации на периферии, но увеличивается однородность

структуры слитка, увеличивается микропористость и величина

ветвей

дендритов. Так как диаметр слитка, и соответственно, диаметр отверстий в

литейной оснастке малы, то во избежание замерзания расплава, особенно в

начальной стадии литья, необходим его перегрев.

Напряжение на индукторе при заданной высоте жидкой зоны

определяется размерами слитка и частотой тока. С увеличением частоты тока

нагрузки напряжение увеличивается пропорционально частоте.

Напряжение

контролируется и поддерживается постоянным или регулируется системой

автоматического регулирования размеров слитка. Высота жидкой зоны

существенно влияет на процесс кристаллизации. Колебания высоты жидкой

зоны приводят к колебанию размера слитка.

Равномерность и количество охлаждающей жидкости существенно

влияет на устойчивость процесса литья и структуру слитка. Расположение

пояса охлаждения должно быть таким, чтобы фронт

кристаллизации

287

находился на уровне середины высоты индуктора, где величина

электромагнитного усилия максимальна.На рис. 1.6.13 представлен процесс

начального формирования слитка в электромагнитном кристаллизаторе.

Рис. 1.6.13 – Формирующийся слиток

При выборе габаритных размеров ЭМК необходимо руководствоваться

следующими факторами: размерами получаемых слитков, энергетическими

затратами на производство слитка и удобством подачи металла в

кристаллизатор.

Наилучшие энергетические характеристики имеет индукционная

установка, в которой внутренний диаметр ЭМК имеет размеры, близкие к

размерам отливаемых слитков. Проведенные на экспериментальной

установке исследования показали, что при заданном диаметре

слитков,

внутренний диаметр индуктора должен лежать в диапазоне

сл

D)4,12,1(



причем большие значения в представленном диапазоне необходимо

принимать для слитков меньшего поперечного сечения с целью обеспечения

удобства подачи металла в ЭМК. При переходе литья от слитков больших

диаметром на слитки с меньшим диаметром если их диаметры отличаются не

более чем на 30%, литье можно вести без смены кристаллизатора, что не

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Федеральное государственное образовательное учреждение

высшего профессионального образования

«Сибирский федеральный университет»

С.Ф. Сарапулов Ф.Н. Сарапулов Т.В. Тимофеева Т.А. Колпакова

Структурное моделирование

Учебное пособие по самостоятельной работе

Красноярск 2007 г.

УДК

ББК

Рецензенты:

Сарапулов Ф.Н. и др.

Структурное моделирование: учебное пособие по самостоятельной

работе/ Ф.Н. Сарапулов, С.Ф. Сарапулов, Т.В. Тимофеев, Т.А. Колпакова

– Красноярск: ФГОУ ВПО «Сибирский федеральный университет», 2007

ISBN

В пособии изложены основы синтеза структурных схем и

математических моделей в переменных

состояния для

электромеханических систем и их элементов. Сформулированы

методические процедуры преобразования структурных схем к

детализированным. Приведены примеры исследования переходных

процессов в различных электрических цепях и устройствах с

использованием структурных схем.

Учебное пособие предназначено для бакалавров и магистров по

направлению 140200 «Электроэнергетика и электротехника».

УДК

ББК

 ФГОУ ВПО

«Сибирский

федеральный университет»

СОДЕРЖАНИЕ

ВВЕДЕНИЕ.............................................…………………..…………………...5

Глава 1. СТРУКТУРНЫЙ СИНТЕЗ ДИНАМИЧЕСКИХ

МОДЕЛЕЙ ЭЛЕКТРОТЕХНИЧЕСКИХ УСТРОЙСТВ…………...8

1.1. Описание структурного метода ......................…………………………...8

1.2. Синтез динамических моделей цепей ………………………….............11

Глава 2. МОДЕЛИРОВАНИЕ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ........................21

2.1. Последовательная двухэлементная RL-цепь ...………………………...21

2.2. Последовательная трехэлементная RLC-цепь....……………………….28

2.3. Сложная цепь с несколькими источниками питания…………………..32

2.4. Индуктивно связанные цепи ………………………............……………37

2.5. Трехфазные цепи…………………………………………………………45

2.6. Модели

резистивных цепей……………………………………………...55

2.7. Катушка индуктивности с ферромагнитным сердечником……………59

Глава 3. МОДЕЛИРОВАНИЕ ТРАНСФОРМАТОРОВ……………............65

3.1. Идеальный трансформатор.…………………………….......……………65

3.2. Реальный трансформатор………………...………...........………………69

Глава 4. МОДЕЛИРОВАНИЕ ИНДУКЦИОННЫХ МАШИН

С РАЗОМКНУТЫМИ И ЗАМКНУТЫМИ

МАГНИТОПРОВОДАМИ ……………..............…………………..75

4.1. Динамические модели линейных индукционных машин .....……….....75

4.2. Аналитическая модель ЛАД в осях координат , ..…………………..86

4.3. Численная модель ЛАД с многофазной кольцевой обмоткой

"фаза-

паз" …...……………………………………....................................93

4.4. Модель индуктора с барабанной обмоткой .............………………….107

4.5. Модель ЛАД в программе SIMULINK .....................………………….113

4.6. Определение статических характеристик ЛАД ...........……………….143

4.7. Моделирование ЛАД в замкнутой системе электропривода ………..146

4.8. Структурные схемы тепловых цепей ЛАД ................………………...150

Глава 5. МОДЕЛИРОВАНИЕ МЕХАНИЧЕСКИХ

ПРЕОБРАЗОВАТЕЛЕЙ ЭЛЕКТРОПРИВОДОВ.........................157

5.1. Функции механических преобразователей ..............…………………157

5.2. Структурный метод синтеза обобщенных моделей механических

преобразователей ………………………………………......................159

5.3. Электропривод при жестких линейных механических связях............164

5.4. Преобразователи с упругими связями .………………………………..221

БИБЛИОГРАФИЧЕСКИЙ СПИСОК ..........................................…………293

ВВЕДЕНИЕ

Разработка методов и универсальных математических моделей для

исследования динамических режимов работы электромеханических

систем является весьма актуальной задачей, что можно объяснить

постоянным стремлением исследователя наиболее полно отразить в

модели особенности объекта (усложнить модель), с одной стороны, и

представить его как элемент системы (по возможности упростить

модель), с другой. Удачным компромиссным

выходом при выполнении

этих противоречащих друг другу требований представляется

использование теории цепей, методы расчета которых достаточно

хорошо разработаны в теооретической электротехнике [5, 12, 22]. При

разумной детализации цепи, соответствующей объекту, можно

обеспечить приемлемую точность результатов расчета путем введения

соответствующих параметров цепи (параметрически). Во многих

случаях при исследовании нестационарных процессов другой

физической природы оказывается весьма

удобным и эффективным

использование аппарата аналоговых схем замещения, которые с

формально математической точки зрения решаются теми же методами,

что и применяемые в электротехнике. Достаточно назвать примеры

исследования магнитных процессов в устройствах на основе магнитных

цепей и тепловых процессов – с помощью тепловых цепей [7].

Традиционный подход к анализу электромеханических

преобразователей энергии предполагает

использование моделей типа

«поле – цепь», когда особенности распределения мгновенных значений в

зоне энергопреобразования исследуются с помощью «полевых»

численных моделей, а изменение во времени интегральных величин

устройства (токов, усилий, мощностей) в динамических режимах – с

помощью «цепных» моделей (схем замещения), параметры которых

определяются на первом этапе решения задачи и далее могут

корректироваться

в ходе расчетов. Однако практически во всех случаях

можно остаться в рамках цепного подхода, используя вместо моделей

«поле – цепь» модели типа «детализированная цепь – цепь». Это вполне

логично, поскольку детализированная цепь получается на основе

конечно-разностной сетки полевой модели (метод конечных разностей)

при укрупнении шага сетки. Такие модели удобны еще и

тем, что они

допускают построение своего рода гибридных вариантов, когда

детализированная цепь исследуемой области соединяется с

«интегральной» (укрупненной) цепью другой области, не требующей к

себе повышенного внимания с позиций как точности расчетов, так и

влияния ее на процессы в устройстве.

Удобным инструментом анализа динамических режимов работы

электромеханической системы и ее цепей является аппарат

структурных

схем, широко применяемых при исследовании электроприводов и систем

управления ими. Данный подход эффективно использует достоинства метода

визуального программирования и компьютерные пакеты типа SIMULINK

(приложение к Matlab) с ориентацией на современную вычислительную

технику. Иерархическая структура моделей позволяет наполнять библиотеку

новыми модулями, на отвлекаясь каждый раз на рутинные операции синтеза

исходных элементов («строительных

блоков»).

Следует отметить, что в компьютерной модели каждое звено

структурной схемы выполняет математические операции (вычислительные

процедуры) над переменными во временной области, хотя передаточные

функции звеньев записываются в операторной форме [3]. При этом легко

формируются каналы вычисления мгновенных значений мощностей и

электромагнитных усилий электромеханической системы как произведения

соответствующих переменных, а нелинейность ее параметров

учитывается

при помощи типовых блоков нелинейностей или дополнительных

функциональных преобразователей величин.

Применение детализированных структурных схем (ДСС), которые

отличаются детализацией алгоритмов вычислений до элементарных

операций, позволяет легко выделять линейные и нелинейные области

модели, наращивать ее дополнительными элементами в соответствии с

расширением реальной электротехнической системы. Линейная часть модели

может быть преобразована по

обычным правилам преобразования

структурных схем [19], хотя при этом зачастую теряется топологическое

соответствие модели реальной структуре. Чтобы исключить необходимость

свертывания схемы при наличии алгебраических контуров, в ряде случаев

бывает полезно превратить их в искусственно динамические путем

включения фильтров с малыми постоянными времени, как показано в главе

2.6.

Модель «запускается», как и реальная

система, с нулевых начальных

условий и выходит далее на исследуемые режимы работы. В случае

необходимости ненулевые начальные условия учитываются путем

включения на выходы соответствующих интеграторов дополнительных

блоков, суммирующих начальные значения переменных с выходными

сигналами интеграторов, или соответствующим редактированием их