Тихоненков В.А. Конструирование и надежность измерительно-вычислительных комплексов летательных аппаратов

11

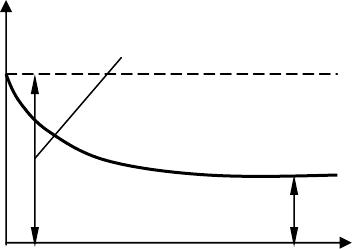
График изменения интенсивности отказов во времени приведен на рис.

1.1. Если

λ

2

>

λ

1

, тогда для времени t

→

∞

, члены содержащие

t

e

⋅

−

2

λ

малы и

λ

(t)

→

λ

1

.

λ

Если t → 0, то значения c

1

⋅λ

1

+ c

2

⋅λ

2

t

е

⋅

−

1

λ

и

t

е

⋅

2

λ

близки

к единице, тогда интенсив-

ность отказов при суперпо-

зиции двух показательных

λ

1

функций будет равна сумме

t

λ

(t)

≈

c

1

⋅λ

1

+ c

2

⋅λ

2

Рис 1.1

1.2. Сохраняемость неремонтируемых систем.

Неремонтируемые изделия могут находится в процессе эксплуатации в

состоянии хранения или транспортирования, когда они не функционируют.

Иногда эти условия могут приближаться к условиям работы, в том случае,

когда они хранятся не на складе, а установлены на объекте, но не работают.

При этом хранение и транспортирование их осуществляется при условиях

хранения и транспортирования объекта.

В этих условиях надежность системы характеризуется параметром , на-

зываемым сохраняемостью.

Сохраняемость это свойство изделия поддерживать свои эксплуатаци-

онные показатели в течение и после срока хранения и транспортирования, ус-

тановленные технической документацией. То есть изделие не работает но

всегда готово к работе. Здесь случайной величиной является срок сохраняе-

мости Т

с

до отказа. То есть, если просто будет стоять, то сколько простоит

до отказа.

Случайный срок сохраняемости Т

с

до отказа обычно имеет экспоненци-

альный закон распределения вероятностей, дифференциальная форма которо-

го является плотностью распределения отказа:

)exp()( ttf

ccc

⋅

−

⋅

=

λ

. (1.9)

где

λ

с

– интенсивность отказов изделия при хранении, обычно

λ

с

= (0,01

– 0,001)

λ

;

λ

– интенсивность отказов изделия, когда оно функционирует.

12

Зная плотность распределения срока сохраняемости можно определить

количественные показатели, характеризующие надежность изделия в услови-

ях хранения.

Вероятность безотказного хранения изделия:

( ) ( )

∫ ∫

⋅−⋅−

=⋅−=−=

t t

tt

cc

edtedttftP

0 0

11

λλ

λ

. (1.10)

Средний срок сохраняемости изделия:

∫ ∫

∞ ∞

=⋅−==

0 0

1

)exp()(

c

cссрс

dttdttРТ

λ

. (1.11)

Так как

λ

с

<<

λ

, то Т

ср с

>> Т

ср

, где Т

ср

– среднее время безотказной

работы изделия. Обычно среднее время безотказной работы Т

ср

составляет

тысячи или десятки тысяч часов, а средний срок сохраняемости Т

ср с

– года

или десятки лет.

1.3. Долговечность неремонтируемых систем.

Таким образом, надежность неремонтируемых систем характеризуется

двумя показателями:

- безотказностью Т

ср

– когда изделие функционирует и сохраняет

работоспособность;

- сохраняемостью Т

ср с

– когда изделие не функционирует но сохра-

няет готовность к нормальному функционированию.

Еще одним свойством изделия непосредственно связанным с надежно-

стью является его долговечность.

Долговечность – это свойство аппаратуры сохранять работоспособность

до предельного состояния, оговоренного в технической документации. Дол-

говечность описывается двумя показателями надежности:

- Ресурсом Т

р

– это величина наработки изделия до предельного со-

стояния, оговоренного в технической документации (обычно единица изме-

рения час);

- Сроком службы Т

сл

– который исчисляется календарной продолжи-

тельностью эксплуатации системы вплоть до момента возникновения его

предельного состояния.

Предельное состояние изделия определяется невозможностью его даль-

нейшей эксплуатации, обусловленной либо снижением его технических ха-

13

рактеристик ниже допустимых технической документации значений, либо по

экономическим, либо по требованиям безопасности использования.

Так как под эксплуатацией понимается время нахождения изделия у по-

требителя с момента его приобретения, то срок службы включает в себя как

время хранения и транспортирования, так и время его непосредственной ра-

боты, то есть:

Т

сл

=Т

ср.с

+Т

ср.р

,

где Т

сл

- средний срок службы;

Т

ср.с

- средний срок сохраняемости;

Т

ср.р

- средний ресурс работы.

Для неремонтируемых систем средний ресурс работы равен средней на-

работке на отказ, то есть Т

ср.р

=Т

ср

.

То есть в данном случае случайными величинами являются два интерва-

ла времени Т

ср.с

и Т

ср.р

, каждый из которых обладает своими показателями на-

дежности.

F

c

(t);P

c

(t);

λ

c

(t) – количественные показатели надежности сохра-

няемости;

F

р

(t);P

р

(t);

λ

р

(t) – количественные показатели надежности безотказ-

ной работы.

Стоит задача определения надежностных характеристик срока службы

Т

сл

, по количественным показателям составных частей. При этом в зависимо-

сти от условий эксплуатации системы делятся на:

- системы одноразового использования – это системы, ресурс работы

которых полностью вырабатывается после хранения за один раз включения

аппаратуры (например, ракетные установки, гидро и электростанции и дру-

гие);

- системы многоразового использования – это системы, у которых

срок хранения разбивается на части, между которыми производится много-

кратная работа изделия (например, корабли, самолеты, технологическое обо-

рудование и так далее)

Соответственно и методы определения Т

ср

и его количественных показа-

телей надежности для каждого случая свой.

1. Системы одноразового использования должны иметь количествен-

ные показатели надежности определенные как композиции на двух последо-

вательный интервалах времени Т

ср.с

и Т

ср.р

.

Воспользовавшись теорией надежности ремонтируемых систем для по-

следовательного свершения событий при стационарных потоках отказов (то

есть среднее число отказов в единичном интервале времени является посто-

янным), тогда в Лапласовых изображениях функция плотности распределе-

ния отказов будет иметь вид [1]:

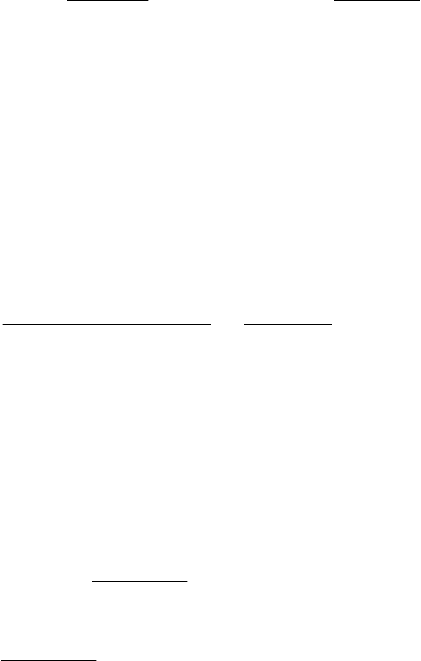
14

∫

=⋅=−⋅=

t

слpcpcсл

SfSfSfdtfftf

0

)()()()()()(

&&&

τττ

где f

сл

(t) – плотность распределения наработки системы за срок службы;

f

с

(

τ

) – плотность распределения отказов за время хранения;

f

р

(t –

τ

) – плотность распределения наработки за время работы системы;

τ

− время хранения системы;

t

o

–

τ

− время работы системы;

)(Sf

c

&

− Лапласовое изображение плотности f

с

(

τ

);

)(Sf

p

&

− Лапласовое изображение плотности f

р

(t –

τ

).

Лапласовые изображения соответственно равны:

p

c

S

Sfи

S

Sf

λ

+

=

+

= )()(

&&

,

где

λ

с

и

λ

р

- соответственно интенсивности отказов в процессе хранения и

работы.

С учетом этих значений, и переходя от изображения к оригиналу, исход-

ное уравнение будет иметь вид:

[

]

t

cp

pc

cлсл

p

c

ee

SS

Sftf

⋅

=

++

⋅

==

λ

λλ

λ

λλ

λ

-

-))((

)()(

&

. (1.12)

Отказ наступает при t = t

c

+ t

p

, причем t

c

и t

p

– независимы.

Зная функцию плотности распределения отказов, можно определить ве-

роятность безотказной работы за срок службы:

[ ]

t

c

t

p

cp

t t t

t

cp

pc

слсл

p

c

p

c

ee

dtedtedttftР

⋅−

∞ ∞ ∞

⋅−

⋅−⋅

−

=













−⋅

−

⋅

==

∫ ∫ ∫

λ

λλ

1

)()(

(1.13)

Аналогично используя Лапласовые изображения, можно определить ин-

тенсивность отказов за срок службы [1]:

15

[

]

t

cp

pc

сл

pc

et

⋅+−

−

+

⋅

=

)(

1)(

λλ

λ

. (1.14)

При больших значениях t = t

c

+ t

p

(t

c

– десятки лет), то есть при t

→

∞

,

значение

0

)(

→

⋅

+

−

t

cp

e

λ

, тогда

cp

pc

cл

t

λλ

λ

+

⋅

=)(

. (1.15)

Тогда при t

→

∞

, срок службы системы одноразового использования для

экспоненциального закона распределения отказов можно представить в виде:

pc

cp

сл

t

Т

λλ

λ

⋅

+

==

)(

1

. (1.16)

2. Системы многоразового использования.

Для определения количественных показателей надежности, последова-

тельность событий которых неизвестны, используют суперпозиционный за-

кон распределения вероятностей [6]. Плотность распределения наработки до

отказа принимается:

f

сл

(t) = c

1

⋅

f

c

(t) + c

2

⋅

f

p

(t) .

где с

2

=Т

ср

/Т

с

; с

1

=1– с

2

– коэффициенты веса, учитывающие влияние различ-

ных слагаемых.

При экспоненциальных законах распределения каждой из составляющих,

плотность распределения наработки до отказа за время службы Т

сл

равна:

t

p

t

cсл

p

c

ecectf

⋅

−

⋅−

⋅⋅+⋅⋅=

λ

λλ

21

)( . (1.17)

Вероятность безотказной работы за срок службы:

t

сл

p

c

ecectР

⋅−

⋅+⋅=

λ

21

)(

. (1.18)

Интенсивность отказов за срок службы:

16

t

p

t

c

сл

p

c

p

c

ecec

t

⋅−

⋅

−

⋅−

⋅+⋅

⋅⋅+⋅⋅

=

λ

λλ

λ

21

)(

. (1.19)

Средний срок службы

рс

ср

рс

сл

сс

Т

λλ

λ

λλ

⋅

+

⋅

=+=

21

. (1.20)

Так как

λ

с

<<

λ

p

то:

- для больших t

→

∞

значение

0

→

⋅

−

t

p

e

λ

, тогда

.)(;)(;)(

11 cсл

t

сл

t

cсл

tectРectf

cc

λλλ

λλ

=⋅=⋅⋅=

⋅−⋅−

- для малых t

→

0 значения

1

→

≈

⋅

t

p

e

c

-

e

λ

, тогда

.)(;)(;)(

212121 рcслслрcсл

ссtсctРсctf

λ

⋅

+

⋅

=

+

=

⋅

+

⋅

=

Кроме среднего значения ресурса Т

ср р

= Т

ср

и среднего срока службы

Т

ср сл

= Т

сл

используют понятия

γ

% и медианного ресурса и срока службы Т

р

γ

;

Т

сл

γ

; и Т

р50

; Т

сл50

.

Гамма-процентный ресурс или срок службы – это тот, который равен

или превышает в среднем заранее заданное число процентов (

γ

) изделий за-

данного типа, не вышедших из строя при испытаниях. Например, если

γ

=95%, то это означает, что не менее 95 из 100 изделий обладают назначен-

ным ресурсом или сроком службы. Таким образом,

γ

определяет вероятность

безотказной работы за время ресурса или срока службы, то есть

∫∫

∞∞

==

слр

Т

сл

Т

p

dttfилиdttf .

100

)(

100

)(

γ

Левые и правые части равенств определяют вероятность нахождения

случайной величины в интервале [Т

γ

;∞]. А в целом эти равенства определяют

каким должен быть Т

γ

, чтобы

γ

% изделий имели Т

γ

лежащем в интервале

времени [Т

γ

;∞].

17

Пусть плотности распределения ресурса и срока службы имеют экспо-

ненциальный закон

t

pp

p

etf

⋅

−

⋅=

λ

)( и

t

слсл

сл

etf

⋅−

⋅=

λ

)(

,

тогда

∫

∞

⋅−⋅−

∞

⋅−⋅−

==+−=−=⋅

γ

λ

λλλλ

р

pp

p

pp

Т

tt

T

tt

р

ee

e

edte .

100

1

|

Логарифмируя, получим:

⋅













=⋅−

100

ln

γ

λ

γ

рр

Т

,

откуда

γ

% ресурс изделия

.

100

ln

1













⋅−=

γ

λ

γ

р

Т

(1.21)

Аналогично,

γ

% срок службы:

.

100

ln

1

γ

λ

γ

⋅=

сл

Т

(1.22)

Если

γ

= 90% (наиболее часто задаваемое в ТЗ на разработку), то есть

90% и более изделий имели ресурс или срок службы, заданной в ТЗ, то:

сл

слсрр

pр

р

ТТилиTТ 1,0

1

1,01,0

1

1,09,0ln

1

9090

===≈⋅−=

λλλ

То есть средние ресурс и срок службы в 10 раз больше чем

γ

= 90% ре-

сурс и срок службы , что соответствует

γ

% ресурсу и сроку службы при

γ

≈36,6%. Действительно, вероятность безотказной работы для экспоненциаль-

ного закона распределения при t = T

ср

может быть представлена в виде:

%6,36366,0)(

1

======

−−

⋅

−

⋅−

ееeetР

ср

T

t

λλ

λ

18

1.4. Юридическо-правовые понятия надежности.

Кроме указанных количественных характеристик долговечности, а

именно:

γ

%, медианных и средних ресурсов, сроков хранения и сроков служ-

бы в паспортах и описаниях на изделия устанавливаются так называемые га-

рантийные ресурс, срок хранения и срок службы.

Эти понятия юридические, как известно в течение гарантийного срока

службы завод изготовитель принимает претензии по качеству выпущенных

изделий.

Гарантийный срок службы, хранения и ресурс находятся по кривым

убыли надежности при наработке и при хранении. При этом предприятие за-

дается гарантийной вероятностью безотказной работы Р

рг

, гарантийной веро-

ятностью срока хранения Р

сг

и гарантийной вероятностью срока службы Р

слг

и по кривым убыли находят гарантийный ресурс Т

рг

, гарантийный срок хра-

нения Т

сг

и гарантийный срок службы Т

сл г

.

Для экспоненциального закона распределения вероятность безотказной

работы (ресурса), вероятность срока хранения и вероятность срока службы

соответственно имеют вид:

Р

р

(t) = exp(-

λ

p

⋅

t) ; Р

с

(t) = exp(-

λ

с

⋅

t); Р

сл

(t)= exp(-

λ

сл

⋅

t) .

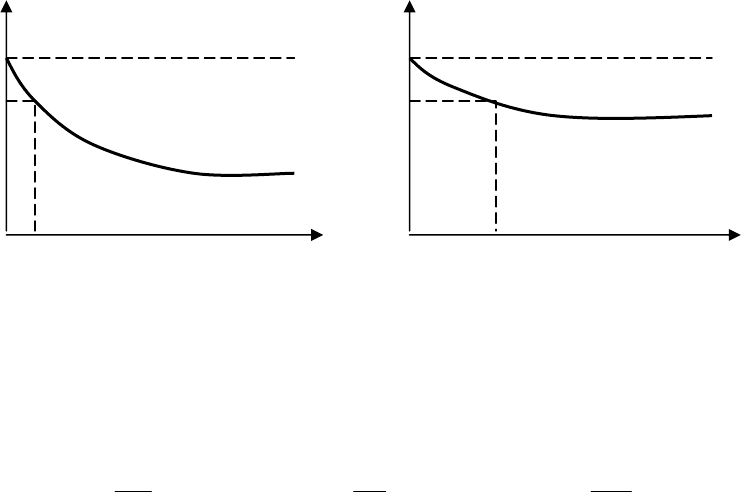
Тогда графически (например, для гарантийных ресурса и срока службы)

это выглядит следующим образом (см. рис. 1.2).

Р

р

(t) Р

сл

(t)

1 1

Р

рг

Р

сл г

Р

сл

(t)= exp(-

λ

сл

⋅

t)

Р

р

(t) = exp(-

λ

p

⋅

t)

t t

Т

рг

Т

сл г

Рис. 1.2.

Аналитически, переходя к

γ

% выражению вероятностей безотказной ра-

боты, срока хранения и срока службы, получим:

рг

р

рг

PТ ln

1

⋅−=

λ

;

сг

с

сг

PТ ln

1

⋅=

λ

;

слг

сл

слг

PТ ln

1

⋅=

λ

(1.22)

19

При назначении гарантийных ресурса, срока хранения и срока службы

завод изготовитель заинтересован в получении минимального количества

рекламаций, поэтому при назначении гарантийных вероятностей Р

рг

, Р

сг

и

Р

сл г

их выбирают близкими к 1. На практике их берут не менее 0,98, что оз-

начает, что к концу гарантийной наработки, гарантийного срока хранения или

гарантийного срока службы 98% всех изделий будут сохранять работоспо-

собность и только 2% изделий необходимо будет заменить в соответствии с

гарантийными обязательствами.

1.5. Задания к выполнению самостоятельной работы.

При испытаниях неремонтируемой системы на отказ и хранение уста-

новлено, что закон распределение отказов близок к нормальному и интенсив-

ность отказов составила:

- при наработке на отказ –

λ

р

(см. табл. 1.1);

- при хранении –

λ

с

(см. табл. 1.1).

Определить для двух режимов эксплуатации – одноразового и многора-

зового использования следующие показатели надежности:

- средний ресурс работы Т

р

;

- средний срок хранения Т

с

;

- средний срок службы Т

сл

;

- медианный ресурс Т

р50

;

- медианный срок хранения Т

с50

;

- медианный срок службы Т

сл50

;

-

γ

% ресурс Т

р

γ

при

γ

= N

1

% (см. табл. 1.1);

-

γ

% срок хранения Т

с

γ

при

γ

= N

2

% (см. табл. 1.1);

-

γ

% срок службы Т

сл

γ

при

γ

= N

3

% (см. табл. 1.1);

- гарантийный ресурс при вероятности безотказной работы Р

рг

(см.

табл. 1.1);

- гарантийный срок хранения при вероятности безотказного хране-

ния Р

сг

(см. табл. 1.1);

- гарантийный срок службы при вероятности безотказной службы

Р

слг

(см. табл. 1.1).

если известно:

- вероятность безотказной работы Р(t) за время t

1

(см. табл. 1.1);

- вероятность безотказного хранения Р(t) за время t

2

(см. табл. 1.1);

- вероятность безотказной службы Р(t) за время t

3

(см. табл. 1.1);

Времена t

1

, t

2

, t

3

заданы в процентах от Т

р

, Т

с

, Т

сл

соответственно.

20

Таблица 1.1.

№

вар.

λ

λλ

λ

р

×

××

×10

-

4

[1/час]

λ

λλ

λ

с

×

××

×10

-

6

[1/час]

N

1

[%]

N

2

[%]

N

3

[%]

Р

рг

Р

сг

Р

сл г

t

1

[%]

t

2

[%]

t

3

[%]

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

0,5

0,7

0,9

1,0

1,2

1,3

1,5

1,7

1,8

2,0

2,2

2,3

2,5

2,7

2,8

3,0

2,9

2,6

2,4

2,1

1,9

1,6

1,4

1,1

0,9

0,6

0,4

3,2

3,5

3,7

5,0

4,8

4.7

4,5

4,3

4,2

4,0

3,8

3.7

3,5

3,3

3,2

3,0

2,8

2,7

2,5

2,3

2,2

2,0

2,1

2,4

2,6

2,9

3,1

3,4

3,6

3,9

4,1

4,4

4,6

75

77

78

80

82

83

85

87

88

90

89

86

84

81

79

76

75

77

78

80

82

83

85

87

88

90

89

86

84

81

90

89

88

87

86

85

84

83

82

81

80

79

78

77

76

90

89

88

87

86

85

84

83

82

81

80

79

78

77

76

61

62

63

64

65

66

67

68

69

70

71

72

73

74

75

61

62

63

64

65

66

67

68

69

70

71

72

73

74

75

0,995

0,993

0,990

0,987

0,985

0,983

0,980

0,977

0,975

0,976

0,978

0,979

0,981

0,982

0,984

0,995

0,993

0,990

0,987

0,985

0,983

0,980

0,977

0,975

0,976

0,978

0,979

0,981

0,982

0,984

0,960

0,961

0,962

0,963

0,964

0,965

0,966

0,967

0,968

0,969

0,970

0,971

0,972

0,973

0,974

0,973

0,972

0,971

0,969

0,968

0,967

0,966

0,965

0,964

0,963

0,962

0,961

0,960

0,959

0,958

0,950

0,951

0,952

0,953

0,954

0,955

0,956

0,957

0,958

0,959

0,960

0,961

0,962

0,963

0,964

0,950

0,951

0,952

0,953

0,954

0,955

0,956

0,957

0,956

0,955

0,954

0,953

0,952

0,951

0,950

30

35

40

45

50

55

60

65

70

75

80

75

70

65

60

30

35

40

45

50

55

60

65

70

75

80

75

70

65

60

80

75

70

60

55

50

45

30

35

40

45

50

55

60

65

80

75

70

60

55

50

45

30

35

40

45

50

55

60

65

45

46

47

48

49

50

51

52

53

54

55

56

57

58

59

60

61

62

63

64

65

66

67

68

69

70

71

72

73

74

Провести сравнение рассчитанных показателей надежности для однора-

зового и многоразового использования неремонтируемой системы и объяс-

нить причину их расхождения.

Расчетные данные занести в таблицу 1.2.

Таблица 1.2.

Условия

эксплуатации

λ

λλ

λ

сл

[1/час]

Т

р

[час]

Т

с

[год]

Т

сл

[год]

Т

рγ

γγ

γ

[час]

Т

сγ

γγ

γ

[год]

Т

слγ

γγ

γ

[год]

Т

р50

[час]

Т

с50

[год]

Т

сл50

[год]

Т

рг

[час]

Т

сг

[год]

T

сл г

[год]

P(t)

P

c

(t)

Р

сл

(t)

Одноразовая

Многоразовая

Тихоненков В.А. Конструирование и надежность измерительно-вычислительных комплексов летательных аппаратов

Подождите немного. Документ загружается.