Теорія ймовірностей та математична статистика
Подождите немного. Документ загружается.

81
Розділ 3
СИСТЕМИ ВИПАДКОВИХ ВЕЛИЧИН
3.1. ЗАКОНИ РОЗПОДІЛУ СИСТЕМИ ВИПАДКОВИХ
ВЕЛИЧИН І ВИПАДКОВИХ ВЕЛИЧИН,
ЯКІ ВХОДЯТЬ ДО СИСТЕМИ
Сукупність випадкових величин
(
)
,,...,,
21 n
XXX
які розгляда-
ються спільно, називається системою
n
випадкових величин.
Якщо
,n 2
=
тобто розглядається система двох випадкових вели-
чин
()
YX ,
, то геометрично її можна тлумачити як випадкову точ-
ку з координатами
()
YX ,
на площині
XOY
або як випадковий ве-
ктор, складові якого — випадкові величини
. i YX
Аналогічно,
якщо
3
=
n
, то маємо випадкову точку
(
)
ZYX ,,
або випадковий
вектор у тривимірному просторі. У загальному випадку систему
n
випадкових величин можна інтерпретувати як випадкову точку
або випадковий вектор у просторі
n
вимірів.
Розглядають системи дискретних випадкових величин, непе-
рервних випадкових величин, а також системи, до яких входять
як дискретні, так і неперервні випадкові величини. Закони розпо-
ділу систем випадкових величин задаються різними способами.
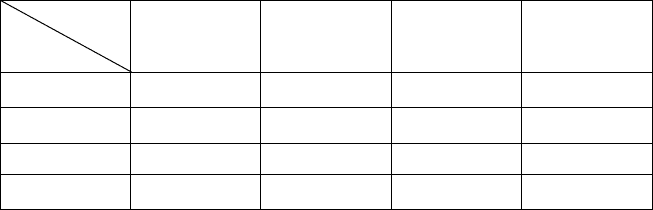
Так, закон розподілу системи двох дискретних випадкових вели-
чин можна задати таблицею:
i
y
i
x
1
y
2
y
…
n
y
1
x
11
p
12
p
…
n
p
1
2
x
21
p
22
p
…
n
p
2
… … … … …
m
x
1m
p
2m
p
…
mn
p
У цій таблиці
(
)
.;
jiij
yYxXPp ===
Функція розподілу
(
)
yxF ,
системи двох випадкових величин ви-
значає ймовірність спільного настання двох подій:
; i yYxX <
<
82
()( )
.;, yYxXPyxF
<<=
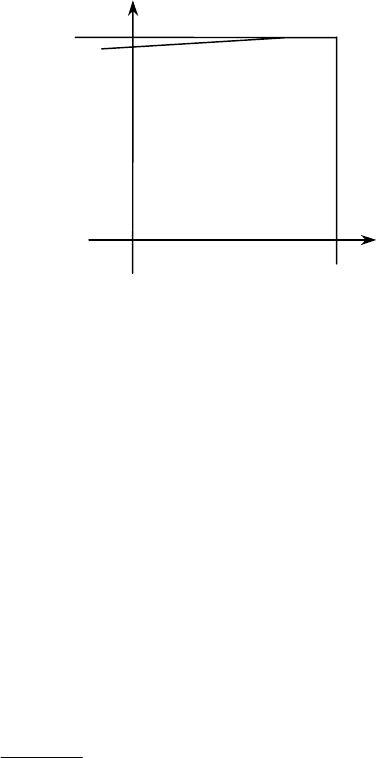
Геометрично функцію розподілу можна
інтерпретувати як імовірність потрапляння випадкової точки в
нескінченний прямокутник із вершиною
(
)
,, yx
обмежений згори і
праворуч (рис. 3.1).
Х
Y
О
M
(
x
; y)
Рис. 3.1
Функція розподілу має такі властивості:
1)
()
1; , 0
≤≤
yxF
2)
(
)
yxF ,
— неспадна функція х і y;
3)
(
)( )
(
)
;0,,,
=−∞=−∞=−∞−∞
yFxFF
4)
(
)
;1,
=+∞+∞
F
5)
(
)()
(
)
(
)
., ,,
21
yFyFxFxF
=∞+=+∞
Функції
() ()
yFxF
21
i
визначають закони розподілу для випад-
кових величин
, i YX
які входять до системи.
За допомогою функції розподілу можна подати ймовірність
потрапляння випадкової точки у прямокутник, сторони якого па-
ралельні осям координат:
()
(
)
(
)
(
)( )
.,,,,,
112112222121
yxFyxFyxFyxFyYyxXxP
+−−=<≤<≤
Якщо розглядається система неперервних випадкових вели-
чин, то для неї визначається щільність розподілу
()
()
.
,
,
2
yx
yxF
yxf
∂∂
∂
=
При цьому
(
)
yxf ,
має такі властивості:
1)
(
)
;0,
≥
yxf
2)
()
∫∫
∞
∞−
∞
∞−
= .1, dxdyyxf

83
Імовірність потрапляння випадкової точки
(
)
yx,
у довільну
область D подається формулою:
(
)
(
)
(
)
∫∫
=
∈
D
dxdy.x,yfDx,yP
Функція розподілу системи двох випадкових величин виража-
ється через щільність розподілу:
() ()
∫∫
∞−∞−
=
x
y
dudvvufyxF ,,.
Коли відомий закон розподілу системи випадкових величин,
то можна знайти закони розподілу для її складових. Якщо в таб-
лиці задано закон розподілу системи
(
)
,,YX
то ймовірності
(
)
()
ji
ypxp i
визначаються за формулами:
()
(
)
∑∑
==
====
m
i
ijj
n
j
iji
njpypmipxp
11
....,,2,1 , ;...,,2,1 ,
Скориставшись властивостями функції розподілу системи не-
перервних величин, можна знайти щільності розподілу величин,
які входять до цієї системи:
() () () ()
∫∫
∞
∞−
∞
∞−
== ., ,,
21
dxyxfyfdyyxfxf
Умовним законом розподілу випадкової величини
, яка нале-
жить системі, називається закон розподілу, знайдений за умови,
що друга випадкова величина набула певного значення.
Умовні щільності розподілу визначаються за формулами:
()
(
)
()
(
)
()
()
(
)
()
(
)
()
.
,
,,
/ ;
,
,,
/
1
2
2
1
∫∫
∞
∞−
∞
∞−
====
dyyxf
yxf
xf
yxf
xyf
dxyxf
yxf
yf
yxf
yxf
Для умовних законів розподілу розглядають числові характе-
ристики — умовне математичне сподівання і умовну дисперсію,
які обчислюються за формулами:
() () ()
()
()()
;/// ,//
2
2
2
xYMxYMxYDdyxyyfxYM −==
∫
∞
∞−
() () ()
()
()()
./// ,//
2
2
1
yXMyXMyXDdxyxxfyXM −==
∫
∞
∞−

84
Формули, які виражають умовні математичні сподівання, на-
зиваються
рівняннями регресії першого роду
.
Випадкові величини, які входять до системи, незалежні, якщо
умовні закони розподілу для них збігаються з безумовними. Як-
що щільність розподілу системи величин подається як добуток
функцій, кожна з яких залежить тільки від однієї змінної, то ве-
личини, які входять до системи, незалежні.
Приклади розв’язування задач
Приклад 1
. Система випадкових величин
(
)
YX , із не-
від’ємними складовими має функцію розподілу
()
=yxF ,
(
)
. 0 ,0 1 >β>α+−−=
β−α−β−α− yxyx
eee Знайти
()
i , yxf
()
.32 ;21
<≤<≤
YXP
Дослідити, чи будуть незалежними величи-
ни
, i YX
які входять до системи.
Розв’язання. Обчислимо ймовірність за допомогою функції
розподілу за наведеною раніше формулою:
()
(
)
(
)
(
)
(
)
−−=+−−=<≤<≤
α−2
12,12,23,13,232 ;21 eFFFFYXP
+−++−−++−+−
β−α−β−α−β−α−β−α−β−α−β−
222233323
11 eeeeeeee
=+−−=+−−+
β−α−β−α−β−α−β−α−β−α−β−α−
22233222
1 eeeeeee
(
)
(
)
(
)
(
)
.1111
223 β−α−β−α−α−β−α−α−β−α−
−−=+−++−−= eeeeeee
Для дослідження незалежності
Y
X
i
знайдемо щільність
розподілу системи
()
()
:
,
,
2
yx
yxF
yxf
∂∂
∂
=
()
()
., ;
,
yxyxyxx
eeeyxfee
x
yxF
β−α−β−α−β−α−α−
βα=αβ=α−α=
∂
∂
Щільність розподілу системи подано як добуток двох функ-
цій, кожна з яких залежить від однієї змінної. Отже, величини,
що утворюють систему, незалежні.
Приклад 2. Система випадкових величин рівномірно розподі-
лена в даній області D (рис. 3.2). Знайти
(
)
,, yxf
(
)()
,/ ,
21
xyfxf
()()
xYDxYM / ,/ й умовну ймовірність
(
)
.5,3/6,12,0 =<≤ XYP

85
Х
Y
О
3
5
2
D
Рис. 3.2
Розв’язання. Для визначення щільності розподілу даної сис-
теми випадкових величин скористаємося її властивістю:
()
∫∫
∞
∞−
∞
∞−
=1, dxdyyxf
, а також тим, що в області
D
функція
()
., cyxf =
Тоді
()
;1,
∫∫
=
D
dxdyyxf .1
∫∫
=
D
dxdyc Оскільки даний по-
двійний інтеграл чисельно дорівнює площі області, обчислимо
його як площу трапеції:
.82
2
53
=⋅
+
=
D
S
Тоді
()
(
)
()
⎪
⎩
⎪
⎨
⎧
∈
∉
=
., якщо,
8
1
;, якщо ,0
,
Dyx
Dyx
yxf
Знайдемо щільність розподілу
(
)
.
1
xf
За формулою
()
=xf
1
()
.,
∫
∞
∞−
= dyyxf Якщо значення
x
недодатні, то щільність розподі-
лу системи дорівнює нулю, а отже, щільність
(
)
.0
1
=xf
Якщо
]
3,0(∈x
, то область обмежена лініями y = 0 i y = 2. Маємо,
()
.
4
1
8
1
2
0
1
==
∫
dyxf
Коли
x
змінюється на проміжку
(
]
,5,3
обмежен-
ня області
D
за y такі: знизу y = 0, угорі y = 5 – x. Звідси
()
.
8
5
8
1
5
0
1
x
dyxf
x
−
==
∫
−
Нарешті, якщо
,5>x
(
)
0
1
=xf
(згідно зі зна-
ченням
()
yxf ,
). Запишемо щільність розподілу для Х:
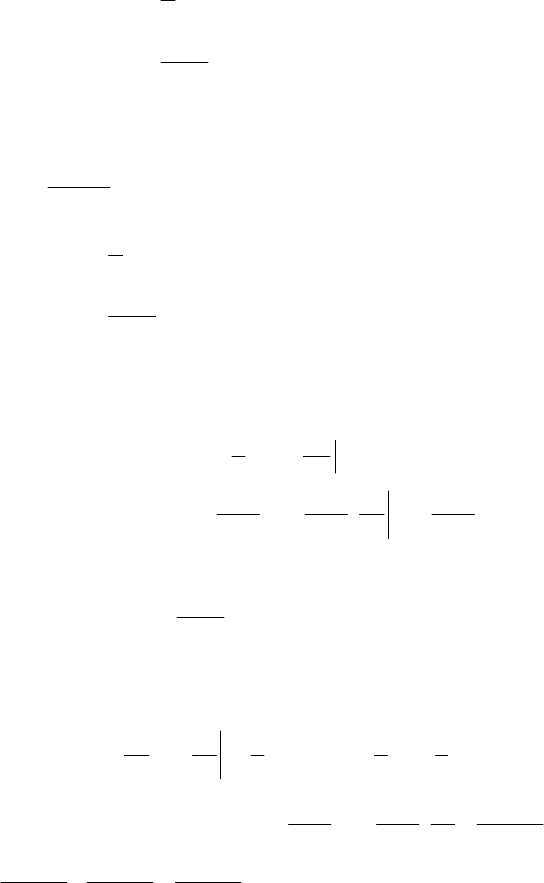
86
()
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
>
≤<
−
≤<
≤
=
.x
;x
x
;x
;x
xf
5 якщо 0,
53 якщо,
8
5
30 якщо ,
4
1
0 якщо ,0
1
Знайдемо умовну щільність розподілу, скориставшись форму-
лою
()
()
()
.
,
/
1
2
xf
yxf
xyf =
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
<<−<<
−
≤<<<
=
.xx, y
x
;x, y
xyf
5350 якщо,
5
1
3020 якщо ,
2
1
/
2
Умовна щільність має два відмінні від нуля аналітичні вирази,
кожний з яких має певне умовне математичне сподівання та дис-
персію.
Якщо
()
,3,0∈x
то
()
1
42
1
/
2
0
2
2
0
===
∫
y
ydyxYM
,
а якщо
()
,5,3∈x
то
()
.
2
5
25
1
5
/
5
0
2
5
0
xy
x
dy
x
y
xYM
x
x
−
=⋅
−
=
−
=
−
−
∫
()
⎪
⎩
⎪
⎨
⎧
<<
−
≤<
=
.53 якщо,
2
5
30 якщо ,1
/
x
x
;x
xYM
Для знаходження умовної дисперсії обчислимо
(
)
./
2
xYM
Якщо
(
]
,3,0∈x
то
()
;
3
4
62
/
2
0
3
2
0
2
2
===
∫
y
dy
y
xYM
()
3
1
1
3
4
/ =−=xYD
,
а якщо
()
,5,3∈x
то
()
()
;
3
5
35
1
5
/
2
3
5
0
2
2
xy
x
dy
x
y
xYM
x
−
=⋅
−
=
−
=
∫
−
()
()
()()
.
12
5
4
5
3
5
/
222
xxx
xYD
−
=
−
−
−
=
87
()
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
<<
−
≤<
=
.x
x
;x
xYD
53 якщо ,
3
5
30 якщо ,
3
1
/
2
Для обчислення умовної ймовірності потрібно зінтегрувати
умовну щільність на відповідному проміжку:
()()
./5,3/6,12,0
6,1
2,0
2
∫
==<≤ dyxyfXYP
Якщо
(
]
5,3∈x
, то значення y обмежені нерівністю
x.y −<
<
50
Тоді при х = 3, 5 верхня межа для значення
.5,1
=
y
Підставляючи
у вираз для умовної щільності значення х = 3,5, маємо:
()
.
15
13
3
2
5,3/6,12,0
5,1
2,0
∫
===<≤ dyXYP
Вправи для самостійного розв’язування
3.1.
Система випадкових величин
(
)
YX ,
рівномірно розпо-
ділена в області, яка являє собою багатокутник із вершинами
A(1,0), B(0,2), C(2,4), D(4,1), E(3,0). Знайти
(
)
,, yxf
()
xf
1
і
()
.3/41,0 =<≤ XYP
3.2.
Область значень системи випадкових величин
(
)
YX ,
—
багатокутник із вершинами
(
)
,0,2
−
A
(
)
,1,2−B
(
)
,1,0C
(
)
.0,1D
Знай-
ти
c (
c
сталий в області),
(
)
yf
2
і
(
)
,6,0/15,1
=
<
≤
−
YXP
як-
що
()( )
., yxcyxf +=
3.3.
Система випадкових величин
(
)
YX ,
має щільність роз-
поділу
()
()( )
222
2516
,
yx
A
yx
++π
=
. Знайти А і функцію розподілу
()
., yxF
3.4.
Координати випадкової точки
(
)
YX ,
розподілені рівномі-
рно у прямокутнику, обмеженому прямими х = 0, х =
,a
,0
=
y
.by
=
Визначити імовірність потрапляння випадкової точки у
круг радіусом R, якщо
ba >
і центр круга збігається з початком
координат.
88
3.5.
Задано щільність розподілу системи випадкових величин
()
YX ,
:
()
(
)
()
.0,0,
22
>>=
+−
yxkxyeyxf
yx
Визначити
k
і закони розподілу випадкових величин, які вхо-
дять до системи.
3.6.
Щільність розподілу системи випадкових величин
()
YX ,
задано формулою:
() ( )
.0,0,
22
>>=
−+−
caAeyxf
cybxyax
Знайти закони
розподілу величин, які входять до системи.
3.7.
Система випадкових величин
(
)
YX , рівномірно розподі-
лена у багатокутнику з вершинами
(
)
,0,1A
(
)
,4,0B
(
)
,4,5C
()
,2,6D
(
)
.0,4F
Знайти
()
yxf ,
і
(
)
.Y/xM
3.8.
Система випадкових величин
(
)
YX ,
рівномірно розподі-
лена у багатокутнику з вершинами
(
)
,0,1A
(
)
,5,3B
(
)
,3,6C
()
.0,5D
Знайти
()
yxf ,
і
(
)
.Y/xM
3.9.
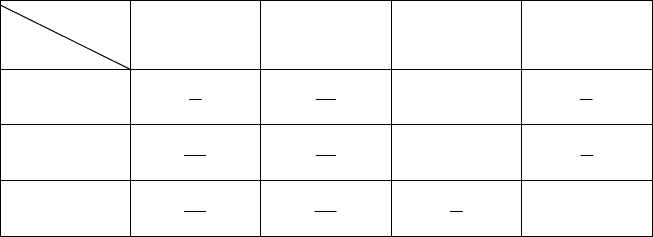
Закон розподілу системи дискретних випадкових величин
задано в табличній формі:
j
y
i
x
2 3 4 5
2
9
1
18
1
—
4
1
3
36
1
18
1
—
6
1
4
36
1
36
5
6
1
—
Знайти закони розподілу величин, які входять до системи,
()()
.3/ i 3/ == YxFYXM
3.2. ЧИСЛОВІ ХАРАКТЕРИСТИКИ СИСТЕМИ
ВИПАДКОВИХ ВЕЛИЧИН
Початковим моментом порядку
rk
+
системи
(
)
YX ,
нази-
вається величина
(
)
rk
rk
YXM ⋅=ν
,
. Якщо
0 ,1
=
=
rk
, маємо
;
0,1
MX=ν
при
1 ,0
=
= rk
дістаємо
.
1,0
MY=ν

89
Центральним моментом порядку
rk
+
називається величи-
на
()
(
)
(
)
rk
rk
MYYMXXM −−=µ
,
. При значеннях
0 ,2
=
=
rk
=µ
0,2
()
.
2
DXMXXM =−=
Якщо навпаки,
2 a ,0
=
=
rk
, то
(
−=
µ
YM
2,0
)
;
2
DYMY =− нарешті, при
1 i 1
=
=
rk
=
11
µ
,
()
(
MXXM −
())
MYY −
XY
K
—
кореляційний момент
(
коваріація
) випадко-
вих величин
. i YX
Його можна обчислити також за формулою:
()
.MYMXXYMK
XY
⋅−=
Для незалежних випадкових величин ко-
реляційний момент дорівнює нулю.
Кореляційний момент характеризує тісноту лінійної залежності
між величинами. З цією самою метою застосовують
коефіцієнт ко-
реляції
.
YX
XY
XY
K
σσ
=ρ
Якщо кореляційний момент (коефіцієнт коре-
ляції) дорівнює нулю, то величини називаються
некорельованими
.
Із незалежності величин випливає їх некорельованість, але із неко-
рельованості величин не випливає їх незалежність. Якщо величини
пов’язані лінійною функціональною залежністю, то
.
XY
1ρ ±=
Для системи випадкових величин
(
)
n
XXX ,...,,
21
числові ха-
рактеристики задаються вектором математичних сподівань
()
n
aaa ,...,,
21
і кореляційною матрицею:
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
=
...
... ... ... ...
...
...
21
22221
11211
nnnn
n
n
KKK
KKK
KKK
K
Якщо елементи цієї матриці поділимо на добуток
ji
YX
σσ
, діс-
танемо матрицю, складену з коефіцієнтів кореляції:
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
=
...
. ...... .....
...
...
R
nn
n
n
1ρρ
ρ1ρ
ρρ1
21
221
112
Приклади розв’язування задач
Приклад 1
. Частка продукції заводу, що містить брак через де-
фект
А, становить 3 %, а через дефект В — 4,5 %. Придатна продук-
ція становить 95 %. Знайти коефіцієнти кореляції дефектів
А і В.
90
Розв’язання.
Розглянемо систему дискретних випадкових ве-
личин
(
)
.,YX
Вони дорівнюють відповідно 1, якщо продукція має
дефект
А або В, і нулю, якщо дефект відсутній. Можливі 4 комбі-
нації значень змінних. Визначимо їхні ймовірності. За умовами
придатна продукція становить 95 %, тому
(
)
.95,00;0 === YXP
Випадкова величина
Х набуває значення 1 з імовірністю 0,03, то-
ді
()
.97,003,010 =−==XP
Отже,
()
(
)
(
)
0;001;0 ==−==== YXPXPYXP
.02,095,097,0 =
−
=
Далі визначаємо такі ймовірності:
(
)( )
−==== 11;1 YPYXP
()
.025,002,0045,01;0 =−===− YXP
Нарешті обчислюємо
(
)
(
)
.955,0045,01110 =−==−== YPYP
Запишемо результати обчислень у таблицю:
X
Y
1 0
()
yp
1 0,025 0,02 0,045
0 0,005 0,95 0,955
(
)
xp
0,03 0,97 1
Для обчислення коефіцієнта кореляції
XY
ρ
визначимо кореля-
ційний момент:
(
)
.MYMXXYMK
XY
⋅−=
Знайдемо значення вели-
чин, які входять до цієї формули:
()
;045,0 ;03,0 ;025,0
2
1
2
1
====
∑∑
==
MYMXpyxXYM
ij
ijji
.02365,0045,003,0025,0 =⋅−=
XY
K
Обчислимо дисперсії
X
і
:Y
;03,0
2
=MX
;0291,0
=
DX
;045,0
2
=MY
;,DY 0429750
=
.669,0
042975,00291,0
02365,0
≈
⋅
=ρ
XY
Приклад 2
. Випадкові величини
YX i
мають відповідно ма-
тематичні сподівання
ba i
, дисперсії
2
2
2
1
i σσ
і коефіцієнт коре-
ляції
.
XY
ρ
Знайти математичне сподівання і дисперсію випадкової
величини
,γ
+
β+α= YXZ
де
γ
β
α
i ,
— сталі.
