Теорія ймовірностей та математична статистика

91

Розв’язання.

Згідно з властивостями математичного сподіван-

ня маємо:

()

.

γ

+

β

+

α

=

γ

+

β

+

α

=

γ

+

β+α= baMYMXYXMMZ

Величини

YX i

залежні. Виведемо формулу для визначення

дисперсії

:Z

()()()()

=γ+β+α−γ+β+α=−=

22

YXMYXMMZZMDZ

()()()()()()

=−β+−α=γ+β+α−γ+β+α=

22

bYaXMbaYXM

() ()()()

(

)

()

+−α=−β+−−αβ+−α=

2

2 aXMbYbYaXaXM

( )() ()

.22

2

22

1

2

σβ+αβρ+σα=−β+−−αβ+

XY

bYMbYaXM

Приклад 3

. Визначити математичні сподівання і кореляційну

матрицю системи випадкових величин

(

)

,,YX

якщо

()

.

yxπ

x,yf

3

22

1

2

++

=

Розв’язання.

Знайдемо числові характеристики системи за на-

веденими раніше формулами:

()

()()

∫∫∫∫

=++++⋅

π

=

++

π

=

−

∞

∞−

∞

∞−

∞

∞−

11

2

12

1

2

22

3

22

3

22

yxdyxdy

yx

xdx

dyMX

(

)

.0

2

1

lim

1

2

22

=

⎟

⎠

⎞

⎜

⎝

⎛

−

++

π

=

∫

∞

∞−

−

∞→

dy

yx

b

Очевидно, що з огляду на симетрію розподілу, математичне

сподівання

Y

також дорівнює нулю.

Визначаємо дисперсії величин, які входять до системи:

=DX

()

∫∫

∞

∞−

∞

∞−

++

π

==

.

1

2

3

22

2

yx

dxx

dyMX

Цей інтеграл обчислюємо, інте-

груючи один раз частинами, а далі переходимо до полярних ко-

ординат.

()

() ()

∫∫

∞

∞−

∞

∞−

=

⎟

⎠

⎞

⎜

⎝

⎛

++

⋅−=

++

=

==

=

++

π

=

;

1

4

1

;

1

; ;

1

2

22

3

22

3

22

2

yx

v

yx

xdx

dv

dxduux

yx

dxx

dyDX

92

() ()

∫∫∫

∞

∞−

∞

∞−

∞

∞−

−

∞→

=

++

π

+

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

++

−

π

=

2

22

2

22

1

2

1

14

lim

2

yx

dx

dydy

yx

x

b

()

∫∫

π∞

=

+

ϕ

π

=

⎟

⎠

⎞

⎜

⎝

⎛

=+

ϕ=

ϕ=ϕ=

=

2

00

2

222

1

2

1

;

;sin;cos

r

rdr

d

ryx

rdrddxdy

ryrx

()

∫∫

ππ

∞→

=ϕ

π

=ϕ

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

+

−

π

=

2

0

2

0

2

.

2

1

4

1

12

1

lim

2

1

dd

r

b

На підставі симетричності щільності розподілу системи має-

мо:

.

2

1

== DXDY

Залишилося знайти

.

XY

K

Математичні споді-

вання

YX i

дорівнюють нулю, а тому

()

∫∫

∞

∞−

∞

∞−

=

++

π

= 0

1

2

1

3

22

yx

xdx

ydyK

XY

(нулю дорівнює внутрішній інтеграл, який було обчислено при

знаходженні математичного сподівання

Х).

Отже,

.

2

1

0

2

1

⎟

⎠

⎞

⎜

⎝

⎛

=K

Вправи для самостійного розв’язування

3.10.

Систему випадкових величин

(

)

YX ,

задано законом роз-

поділу:

X

Y

–1 0 1

–1 0,1 0,3 0,2

0 0,1 0,1 0,05

1 0,05 0,04 0,06

Знайти числові характеристики системи.

93

3.11.

Систему випадкових величин

(

)

YX ,

задано законом роз-

поділу:

X

Y

0 1

–1 0,3 0,2

0 0,2 0,2

1 0,05 0,05

Знайти математичні сподівання та дисперсії величин, які вхо-

дять до системи.

3.12.

Систему випадкових величин розподілено рівномірно в

області, що являє собою трикутник із вершинами

(

)

,0,0O

()

,4,2A

()

.2,4B

Знайти кореляційну матрицю системи.

3.13.

Задано матрицю

K

системи випадкових величин

(

)

ZYX ,,

:

.

25910

998

10816

⎟

⎠

⎞

⎜

⎝

⎛

−

−−

−

=K

Знайти

()

.32 ZYXD ++

3.14.

Скласти кореляційну матрицю для системи випадкових

величин

(

)

,,, ZYX

якщо

,4=σ

X

,2=

XY

K

,6,1−=

XY

K

,4,0=ρ

XY

,5,0−=ρ

XZ

а випадкові величини

Y

Z

i

некорельовані.

3.15.

Випадкові величини

X

та

Y

розподілені нормально з

тими самими параметрами

. i

σ

a

Знайти коефіцієнт кореляції си-

стеми величин

()

,32, YXYX β−αβ+α

якщо

.6,0−=ρ

XY

3.16.

Виконуються чотири незалежні вимірювання тієї самої

величини. Результати вимірювання

,

1

X

,

2

X

,

3

X

4

X

мають одна-

кові математичні сподівання та дисперсії. Розглянемо величини

,

211

XXY −−=

,

322

XXY +=

.

243

XXY −=

Знайти числові характе-

ристики системи

()

.,,

321

YYY

3.17.

.YXZ β+α=

За яких умов

DYDXDZ

22

β+α<

?

3.18.

Вивести формулу для дисперсії добутку двох незалежних

випадкових величин.

3.19.

Значення

X

коливається під впливом випадкових фак-

торів

А і В. Середнє квадратичне відхилення в результаті дії А

дорівнює 1,2, а

В — 1,1. Коефіцієнт кореляції між відхиленнями

дорівнює 0,125. Знайти

X

σ

як результат дії двох факторів.

94

3.20.

Випадкову величину

X

розподілено рівномірно на про-

міжку (–1, 1 ].

m

X

Y

=

(m — ціле число). Знайти

.

XY

ρ

3.21.

Випадкові величини

n

XXX ,...,,

21

мають однакові мате-

матичні сподівання і дисперсії,

0

ρ=ρ

ij

;

1

∑

=

m

i

XY

;

1

∑

+

+=

=

rm

mi

i

XZ

.

1

∑

+=

=

n

mi

i

XU

Для системи

(

)

UZY ,,

знайти кореляційну матрицю.

3.22.

Задано систему випадкових величин

(

)

.,YX

МХ = MY = 0,

DX = 100, DY = 64. При якому значенні

a

випадкові величини

YaXVXU +== i

будуть некорельованими, якщо MXY = 32?

Знайти

. i

DVMV

3.3. ФУНКЦІЇ ДЕКІЛЬКОХ ВИПАДКОВИХ АРГУМЕНТІВ

Нехай задано систему випадкових величин

(

)

YX

,

і функцію

()

.,

YXZ

ϕ=

Потрібно знайти закон розподілу для Z. Якщо

()

YX

,

—

система дискретних величин, то відомі ймовірності

=

ij

p

(

)

ji

yYxXP === ;

і можна знайти ймовірності

(

)

(

)

=ϕ==

jiij

yxzZP ,

.,...,2,1 ;,...,2,1 , njmip

ij

===

А якщо маємо систему неперервних випадкових величин, то

для визначення

()

zf

обчислюємо

(

)

(

)

()

,,

∫∫

=

zD

dxdyyxfzF

де

()

zD

—

область на площині

XOY, в якій

(

)

.,

zyx

<ϕ

Щільність розподілу

(

)

zf

дістаємо диференціюванням функ-

ції розподілу.

Щільність розподілу суми двох випадкових величин

YX

Z

+=

подається формулами:

() ( ) ( )

∫∫

∞

∞−

∞

∞−

−=−= .,, dyyzyfdxxzxfzf

Якщо

YX i

— незалежні випадкові величини, то

()

=yxf ,

() ()

yfxf

21

= і

()

zf

() ( ) ( ) ()

∫∫

∞

∞−

∞

∞−

−=−= .

2121

dyyfyzfdxxzfxf

Нерідко доводиться розглядати суми випадкових величин, ро-

зподілених за нормальним законом. Здобута випадкова величина

— результат підсумовування — має нормальний закон розподілу.

Параметри розподілу додаються в тому разі, якщо величини не-

95

залежні. Додаючи дві нормально розподілені величини із параме-

трами

,

1

aMX

=

,

2

1

σ=DX

,

2

aMY

=

2

σ=DY

і коефіцієнтом коре-

ляції

XY

ρ

, маємо нормальний закон розподілу з параметрами

,

21

aaMZ

+=

.2

21

2

1

σ⋅σρ+σ+σ=

XY

DZ

У загальному випадку закон розподілу функцій двох непере-

рвних випадкових величин визначаємо за такою схемою:

1)

відшукуємо область зміни системи випадкових величин

()

;,

YX

2)

обчислюємо найбільше і найменше значення функції =

Z

()

YX ,ϕ=

у заданій області;

3)

розглядаємо сім’ю кривих

(

)

yxz ,

ϕ

=

і встановлюємо, скі-

льки аналітичних виразів матиме

(

)

;

zf

4)

будуємо лінію

(

)

yxz ,

ϕ

=

і визначаємо

(

)

,

zD

тобто множи-

ну точок, для яких

()

;, zyx

<

ϕ

5)

інтегруємо щільність розподілу на множині

(

)

,

zD

дістаю-

чи

()

;

zF

6)

щоб знайти

()

zf

, диференціюємо функцію розподілу, вра-

ховуючи той факт, що коли:

() ( )

()

(

)

()

(

)

∫∫

ϕ

ψ

=Φ

z

zx

dyyxfdxz

2

1

2

1

,,

,

то

() ( )( )() ()()()()

()

∫

ϕ

ψ

′

ψ−ψ

′

ψ=Φ

′

z

dxzxzxxfzxzxxfz

2

1

.,,,,,,

1122

Числові характеристики функцій можна знайти, визначивши

закон розподілу, а також скориставшись формулами, аналогічни-

ми тим, які застосовувались для функцій одного випадкового ар-

гументу:

()() ( )

∫∫

∞

∞−

∞

∞−

−=ϕ= ;MZMZdxdy; DZx,yfx,yMZ

2

()()()

∫∫

∞

∞−

∞

∞−

ϕ= dxdy.x,yfx,yMZ

2

Деякі розподіли випадкових величин,

що застосовуються в математичній статистиці

Розглянемо деякі розподіли випадкових величин, що застосо-

вуються в математичній статистиці. Вони являють собою функції

кількох випадкових аргументів.

96

1.

Розподіл

.χ

2

Розглядаємо послідовність

n

XXX

,...,,

21

попарно

незалежних випадкових величин, які розподілені нормально з ну-

льовими математичними сподіваннями і одиничними дисперсіями.

Якщо

∑

=

n

i

XU

1

2

,

то ця сума має розподіл

2

χ

з n ступенями во-

лі. Щільність розподілу

()

., ueu

n

uf

un

n

χ

0

2

Γ2

1

2

1

2

>

⎟

⎠

⎞

⎜

⎝

⎛

=

−−

Числові ха-

рактеристики розподілу:

n.n; DUMU 2

=

До виразу щільності

розподілу входить гамма-функція

.

2

0

1

2

dxex

n

x

n

−

∞

−

∫

=

⎟

⎠

⎞

⎜

⎝

⎛

Γ

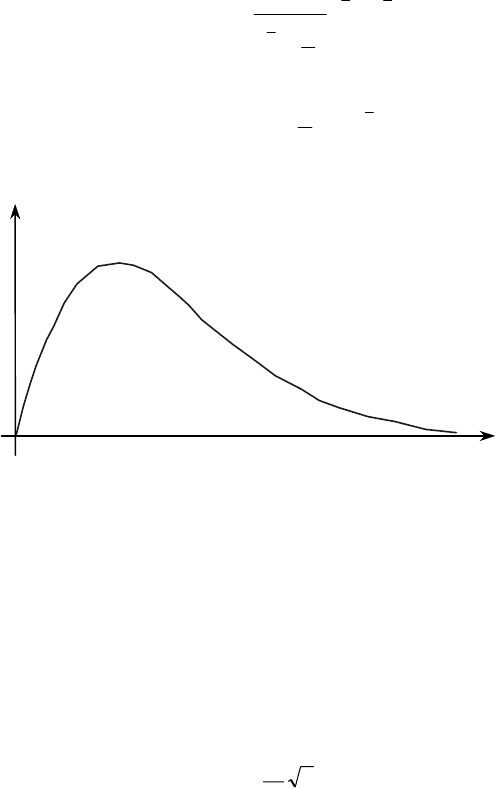
Графік щільності розподілу зображено на рис. 3.3.

Х

f

(

x

)

О

λ

2

Рис. 3.3

Для розподілу

2

χ

складено таблиці виду

()

∫

∞

χ

α

=χ>χ

2

22

dxxfP

для кількості ступенів волі від 1 до 30. У таблицях для заданих

значень імовірностей (здебільшого

;95,0 ;98,0 ;99,0

=

α

0,9; 0,8; 0,7;

0,5; 0,3; 0,2; 0,1; 0,05; 0,02; 0,01; 0,005; 0,002; 0,001) вказано зна-

чення

2

α

χ

для відповідної кількості ступенів волі. Якщо кількість

ступенів волі більша від 30, то розподіл мало відрізняється від нор-

мального з відповідними математичним сподіванням і дисперсією.

2. Розподіл Стьюдента

. Розподіл Стьюдента з n cтупенями

волі має випадкова величина

,

n

V

X

T

=

де Х — нормально розпо-

ділена величина з нульовим математичним сподіванням і одини-

97

чною дисперсією, а

UV

=

. Випадкова величина

U

не залежить

від

Х і має розподіл

2

χ

з n ступенями волі. Щільність розподілу

()

.1

2

1

2

1

2

+

−

⎟

⎠

⎞

⎜

⎝

⎛

+

π

⎟

⎠

⎞

⎜

⎝

⎛

Γ

⎟

⎠

⎞

⎜

⎝

⎛

+

Γ

=

n

t

n

tf

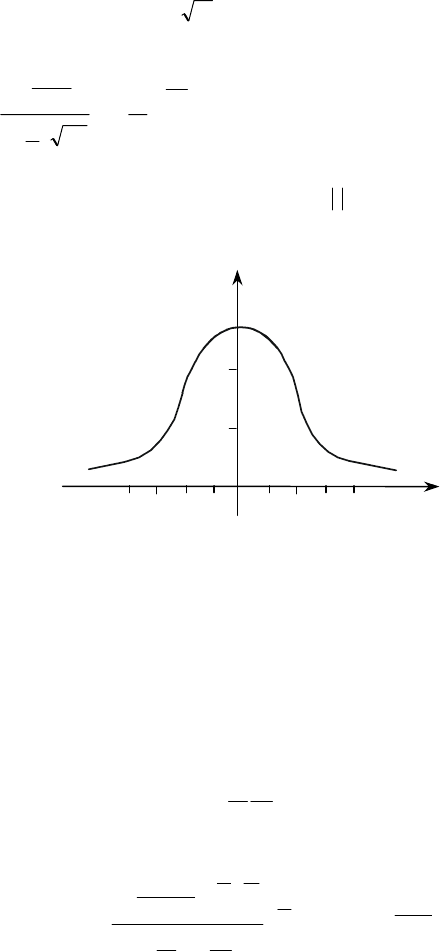
Графік щільності розподілу Стьюдента

за зовнішнім виглядом нагадує нормальні криві. Але вони значно

повільніше спадають до осі

t, якщо

,∞→

t

особливо за малих

значень

n (рис. 3.4).

t

f

(

t

)

О

Рис. 3.4

Складено таблиці розподілу Стьюдента, здебільшого виду

() ( )

,

∫

∞−

=

t

dzzftF

для кількості ступенів волі від 1 до 20. Якщо кіль-

кість ступенів волі більша, то можна застосовувати нормальний

закон розподілу з нульовим математичним сподіванням і одини-

чною дисперсією.

3. Розподіл Фішера

. Якщо випадкові величини

VU

i

неза-

лежні і мають

2

χ

— розподіл відповідно з

21

i

nn

ступенями волі,

то випадкова величина

1

2

n

V

U

F =

має розподіл Фішера з

21

,

nn

ступенями волі. Щільність цього розподілу подається формулою:

() ()

.0 ,

22

2

12

1

2

21

2

1

21

1

21

>+

⎟

⎠

⎞

⎜

⎝

⎛

Γ

⎟

⎠

⎞

⎜

⎝

⎛

Γ

⎟

⎠

⎞

⎜

⎝

⎛

+

Γ

=

+

−

xxnnx

nn

xf

nn

n

nn

F

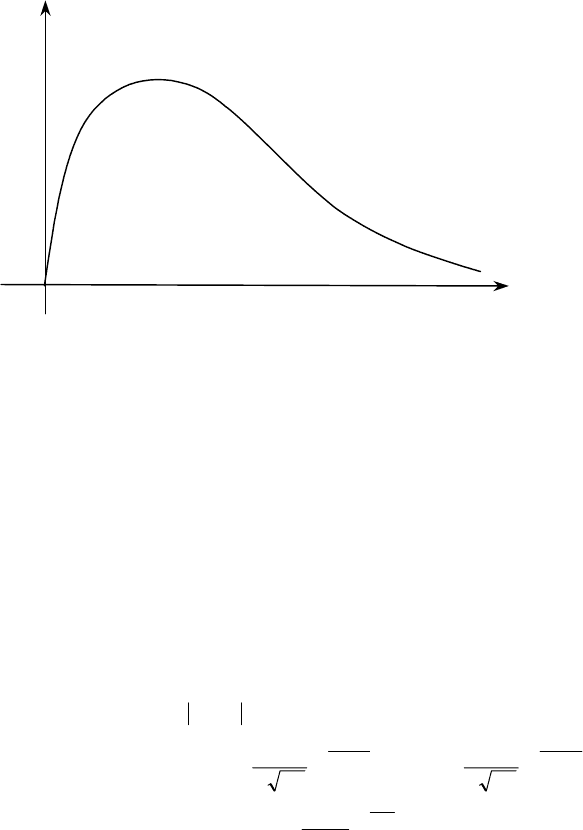
98

Щільність розподілу Фішера має графік, зображений на

рис. 3.5.

Х

f

(

x

)

О

Рис. 3.5

Для розподілу Фішера складено таблиці, в яких для відповід-

ної кількості ступенів волі для ймовірностей

01,0 i 05,0 =α

=

α

наведено значення

α

f

–

(

)

.α=>

α

fFP

Приклади розв’язування задач

Приклад 1

. Махове колесо виготовляється із двох однакових

частин. Маса кожної з них — нормально розподілена величина з

математичним сподіванням, що дорівнює

a

, і дисперсією

.

2

σ

Для балансування колеса важливою є різниця мас зазначених ча-

стин. Знайти закон розподілу заданої випадкової величини.

Розв’язання.

Позначимо масу першої частини літерою Х, а дру-

гої —

Y. Різниця мас

.

YXZ

−=

Закони розподілу

YX i

задаються

щільностями розподілу:

()

,

2

1

2

1

σ

−

πσ

=

ax

exf

()

.

2

1

2

σ

−

πσ

=

ay

eyf

Спільний розподіл

: i

YX

()

()()

(

)

.

2

1

,

22

2

1

2

byax

eyxf

−+−

σ

−

πσ

=

Область

зміни системи

()

YX

,

— уся числова площина, функція Z набуває

невід’ємних значень. При деякому додатному значенні

z побуду-

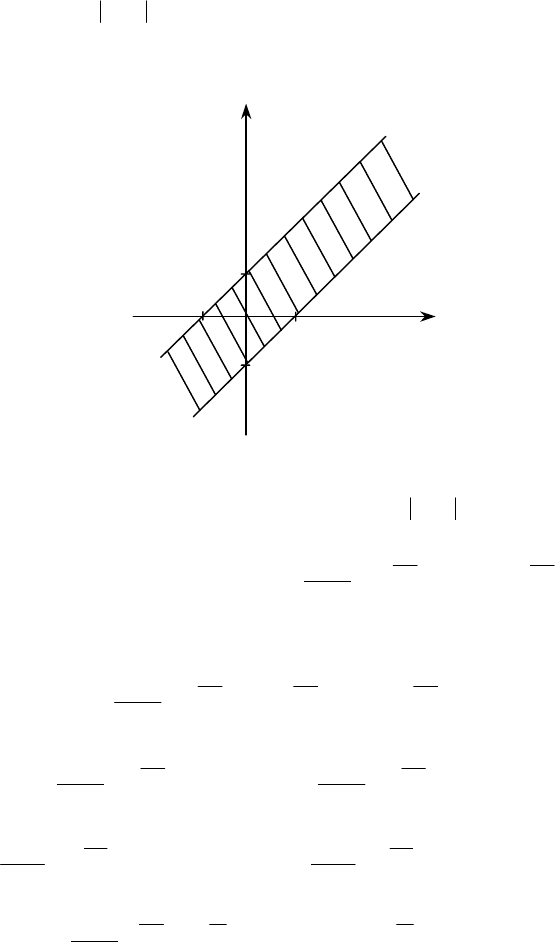
99

ємо область

.

zyx

<−

Ця область обмежена прямими 0=−

−

z

y

x

.0 i =

+

− zyx

Відповідну побудову виконано на рис. 3.6.

Y

D

О

X

Рис. 3.6

Область

()

,

zD

тобто область, для якої

zyx

<−

, лежить між

прямими (на рис. 3.6 її заштриховано). Побудуємо функцію ро-

зподілу:

() ( )

()

() ()

∫∫∫∫

∞

∞−

+

−

σ

−−

σ

−

πσ

== .

2

1

,

2

1

2

1

2

dyedxedxdyyxfzF

zx

ayax

zD

Диференціюючи функцію розподілу, дістаємо щільність роз-

поділу:

()

() () ()

=

⎟

⎠

⎞

⎜

⎝

⎛

+

πσ

=

−−

σ

−−+

σ

−

∞

∞−

−

σ

−

∫

dxeeezf

azxazxax

2

1

2

1

2

1

2

1

()( )

()

()( )

(

)

=

πσ

+

πσ

=

∫∫

∞

∞−

−−+−

σ

−

∞

∞−

+−+−

σ

−

dxedxe

zaxaxzaxax

2222

2

1

2

1

2

1

2

1

()() ()

()

()() ()

(

)

∫∫

∞

∞−

∞

∞−

+−−−+−

σ

−+−+−+−

σ

−

=

πσ

+

πσ

= dxedxe

zaxzaxaxzaxzaxax

2

22

2

22

2

1

2

1

2

1

2

1

()()

()

()()

()

.

2

1

2

22

2

11

2

⎟

⎠

⎞

⎜

⎝

⎛

+

πσ

=

∫∫

∞

∞−

−−−

σ

−

∞

∞−

−+−

σ

−

σ

−

dxedxee

axzaxaxzax

z

100

Для обчислення знайдених невласних інтегралів застосуємо

наведений далі інтеграл, який при

А > 0 виражається за допомо-

гою інтеграла Пуассона:

.

2

A

BAC

CBxAx

e

A

dxe

−

∞

∞−

+±−

π

=

∫

Тоді

()()

()

=

∫

∞

∞−

++−

σ

−

dxe

axzax

2

1

()()

()

.

2

42

1

σ

∞

∞−

+−−

σ

−

πσ=

∫

z

axzax

edxe

Отже, щільність розподілу буде такою:

()

=zf

()

. 0z ,

1

2

1

2

442

2

>

σπ

=πσ

πσ

=

σ

−

σσ

−

zzz

eee

З точністю до сталої дістали так званий напівнормальний за-

кон розподілу.

Приклад 2. Маса деталей — випадкова величина, рівномірно

розподілена на проміжку

(

]

.5,2;2

Знайти закон розподілу маси

двох деталей.

Розв’язання. Позначимо масу однієї деталі літерою Х, а дру-

гої — Y. Вага двох деталей

.YXZ

+

=

Закони розподілу

X

і

Y

і

системи

(

)

YX ,

визначаються через щільності розподілу:

()

⎪

⎩

⎪

⎨

⎧

>

≤<

≤

=

2,5. якщо,0

;5,22 якщо,2

;2 якщо,0

1

x

xf

()

⎪

⎩

⎪

⎨

⎧

>

≤<

≤

=

2,5. якщо,0

;5,22 якщо,2

;2 якщо,0

2

x

yf

()

(

)

()

⎩

⎨

⎧

∈

∉

=

S.yx,

S;yx,

yxf

якщо,4

якщо,0

,

Множину

S

зображено на рис. 3.7.

Наведені раніше формули для визначення закону розподілу суми

двох випадкових величин застосувати не можна, тому розв’яжемо

задачу за загальними правилами. Знайдемо область значень для су-

ми. Очевидно, що

(

]

.5;4∈z

Пряма

zy

x

=

+

проходить через мно-

жину S і, якщо

,5,44

<

< z

перетинає прямі

.2 i 2

=

yx

Область

()

zD

— множина точок, які лежать нижче від прямої. Справді, як-

що підставимо в рівняння прямої, координати, наприклад, точки

(2; 2), то вона задовольняє умову. Отже, якщо

(

)

5,4;4∈z

, то область

()

zD

має такий вигляд, як зображено на рис. 3.8.

Теорія ймовірностей та математична статистика

Подождите немного. Документ загружается.