Теорія ймовірностей та математична статистика

Подождите немного. Документ загружается.

111

У СМО з очікуванням заявка, що надходить у момент, коли

всі канали зайняті, не залишає систему, а стає в чергу на обслуго-

вування.

Процес роботи СМО являє собою

випадковий процес

Процес називається

процесом із дискретними станами

, як-

що його можливі стани

θ,...,θ,θ

можна зарані перелічити, а пе-

рехід системи з одного до іншого відбувається миттєво (стрибко-

подібно). Процес називається

процесом із неперервним часом

якщо моменти можливих переходів системи з одного стану до

іншого не фіксовані заздалегідь, а випадкові.

Процес функціонування СМО являє собою випадковий

процес із дискретними станами та неперервним часом.

Математичний аналіз роботи СМО істотно спрощується, якщо

процес цієї роботи —

марковський

4.3. ПОНЯТТЯ МАРКОВСЬКОГО ПРОЦЕСУ

Випадковий процес називається

марковським

, якщо для будь-

якого моменту часу

імовірнісні характеристики процесу в

майбутньому залежать лише від його стану в даний момент

не залежать від того, коли і як система набула цього стану.

Приклад

. Система

— лічильник у таксі. Стан системи в

момент t характеризується кількістю кілометрів, пройдених ав-

томобілем до даного моменту. Нехай у момент

лічильник по-

казує

Імовірність того, що в момент

tt >

лічильник показу-

ватиме ту чи іншу кількість кілометрів

залежить від

але

не залежить від того, в які моменти часу змінювались покази лі-

чильника до моменту

Деякі процеси можна наближено вважати марковськими.

Приклад

. Система

— група шахістів. Стан системи харак-

теризується кількістю фігур супротивника, що збереглися на до-

шці до моменту

Імовірність того, що в момент

tt >

матеріа-

льна перевага буде на боці одного із супротивників, залежить

насамперед від того, в якому стані перебуває система в даний

момент

а не від того, коли і в якій послідовності зникали фі-

гури з дошки до моменту

112

Аналізуючи випадкові процеси з дискретними станами, зруч-

но користуватися геометричною схемою — так званим

графом

станів

. Зазвичай стани системи зображають прямокутниками

(кручежками), а можливі переходи від одного стану до іншого —

стрілками, що сполучають стани.

Приклад

. Побудувати граф станів такого випадкового проце-

су: пристрій

утворено із двох вузлів, кожний з яких у випадко-

вий момент часу може вийти з ладу, після чого негайно почина-

ється ремонт вузла, який триває протягом зарані не відомого

випадкового часу.

Розв’язання.

Можливі стани системи:

— обидва вузли

справні;

— перший вузол ремонтується, а другий справний;

— другий вузол ремонтується, а перший справний;

— оби-

два вузли ремонтуються.

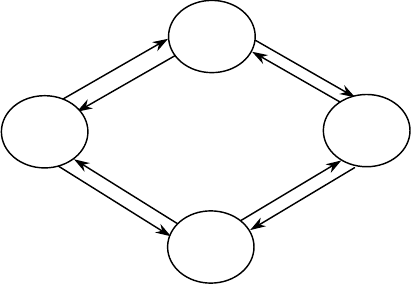
Граф системи наведено на рис. 4.2.

Рис. 4.2

Стрілка, напрямлена із

до

,θ

означає перехід системи в

момент відказу першого вузла; стрілка із

до

— перехід у

момент закінчення ремонту цього вузла. Стрілки із

до

не-

має, оскільки припускається, що вузли виходять із ладу незалеж-

но один від одного.

Для математичного опису марковського випадкового процесу

з дискретними станами і неперервним часом, що відбувається в

СМО, розглянемо одне з важливих понять теорії ймовірностей —

поняття

потоку подій

113

4.4. НАЙПРОСТІШИЙ ПОТІК ПОДІЙ

Потоком подій

називається послідовність подій, які відбу-

ваються одна за одною у випадкові моменти часу. Наприклад,

потік заявок, що надходить до підприємства побутового обслу-

говування, потік викликів до телефонної станції, потік відказів

(збоїв) під час роботи на ПЕОМ тощо. Середня кількість подій,

які відбуваються за одиницю часу, називається

інтенсивністю

потоку

Потік називається

найпростішим

, якщо він має такі власти-

вості:

стаціонарність

— імовірність того, що за деякий промі-

жок часу t відбудеться та чи інша кількість подій, залежить лише

від довжини проміжку і не залежить від початку його відліку,

тобто інтенсивність потоку стала;

відсутність післядії

— імовірність настання деякої кілько-

сті подій на довільному проміжку часу не залежить від того, яка

кількість подій відбулась до початку цього проміжку;

ординарність

— імовірність настання двох і більше подій

за малий проміжок часу t істотно менша за ймовірність того, що

відбудеться одна подія.

Якщо потік подій найпростіший, то ймовірність того, що за

проміжок часу t подія А настане m раз, визначається формулою:

()

(

)

λ−

де

— інтенсивність потоку. Ця формула від-

биває всі властивості найпростішого потоку, а отже, є його мате-

матичною моделлю.

Приклад

. Середня кількість заявок, які надходять до комбіна-

ту побутового обслуговування за 1 год, дорівнює 4. Знайти ймо-

вірність того, що за 3 год надійде: 1) 6 заявок; 2) менш як 6 зая-

вок; 3) не менш як 6 заявок.

Розв’язання.

Нехай подія А — «надходження однієї заявки».

Потік заявок найпростіший. Тому для розв’язування задачі засто-

суємо наведену щойно формулу, в якій

,6<m

.6≥m

Обчислимо відповідні ймовірності.

()

;0249,0

≈=

−

(

)()

(

)

(

)

(

)

(

)

(

)

;0199,15432106

33333333

≈+++++=< PPPPPPmP

(

)

(

)

.9801,00199,01616

333

=−=<−=≥ mPmP

114

4.5. РІВНЯННЯ КОЛМОГОРОВА.

ГРАНИЧНІ ЙМОВІРНОСТІ СТАНІВ

Імовірністю і-го стану

називається ймовірність

(

)

(

)

ni ,...,2,1=

того, що в момент t система перебуватиме у стані

(

)

.,...,2,1 ni =

Очевидно, що для будь-якого моменту t сума ймовірностей

станів дорівнює 1:

()

∑

(1)

Правило побудови рівнянь Колмогорова

. У лівій частині

кожного з рівнянь має бути похідна ймовірності і-го стану. У

правій частині — сума добутків імовірностей усіх станів (з яких

відбувається перехід до даного стану) на інтенсивності відповід-

них потоків подій мінус сумарна інтенсивність усіх потоків, що

виводять систему із даного і-го стану, помножена на ймовірність

цього стану.

Наприклад, для системи

,θ

що має чотири стани

;

, система диференціальних рівнянь Колмогорова для ймовір-

ностей станів набуває такого вигляду:

(

)

002012201100

pppp λ+λ−λ+λ=

′

(

)

113103310011

pppp λ+λ−λ+λ=

′

(

)

223203320022

pppp λ+λ−λ+λ=

′

(

)

332312231133

pppp λ+λ−λ+λ=

′

(2)

У системі (2) незалежних рівнянь на одне менше від загальної

кількості рівнянь. Тому для розв’язування системи необхідно до-

дати рівняння (1) при п = 3.

Особливість розв’язання диференціальних рівнянь взагалі по-

лягає в тому, що потрібно задавати так звані початкові умови, у

даному разі — імовірності станів системи в початковий момент

.0=t

Так, систему (2) маємо розв’язувати за умовою, що в почат-

ковий момент обидва вузли справні і система перебувала у стані

, тобто за початкових умов

(

)

,10

(

)

(

)

(

)

.0000

321

=== ppp

Рівняння Колмогорова дають змогу знаходити всі ймовірності

станів як

функції часу

. Особливий інтерес становить імовірності

системи

()

ni ,...,1=

граничному стаціонарному режимі

тобто при

∞→t

, які називаються

граничними ймовірностями

станів

115

У теорії випадкових процесів доведено, що коли кількість

станів системи скінченна і з кожного з них можна перейти до

будь-якого іншого стану, то граничні ймовірності існують.

Гранична ймовірність стану

має такий зміст: вона показує

середню відносну тривалість перебування системи в цьому стані.

Наприклад, якщо гранична ймовірність стану

становить

5,0

, то це означає, що в середньому половину часу система

перебуває у стані

Приклад 1

. Знайти граничні ймовірності для системи

прикладу, наведеного на с. 114, граф станів якої наведено на

рис. 4.2. При

=λ

Розв’язання.

Система алгебраїчних рівнянь, що описує стаці-

онарний режим для даної системи, належить до виду (1):

⎪

⎩

⎪

⎨

⎧

=+++

;224

;34

;323

3210

302

301

210

pppp

ppp

Розв’язуючи цю систему рівнянь, дістаємо

,4,0

,2,0

,27,0

.13,0

Отже, у граничному стаціонарному режимі

система

в середньому 40 % часу перебуватиме у стані

,θ

20 % —

у стані

,θ

27 % — у стані

,θ

13 % — у стані

.θ

Приклад 2

. Знайти прибуток від експлуатації у стаціонарному

режимі системи

, коли відомо, що за одиницю часу справна ро-

бота першого та другого вузлів приносить дохід, який становить

відповідно 10 і 6 ум. од., а їх ремонт потребує витрат, що станов-

лять відповідно 4 і 2 ум. од.

Оцінити економічну ефективність зменшення вдвічі середньої

тривалості ремонту кожного з цих вузлів, якщо в такому разі до-

ведеться вдвічі збільшити витрати на ремонт.

Розв’язання.

З прикладу 1 випливає, що в середньому перший

вузол справний протягом частки часу, що становить р

+ р

= 0,4 + 0,27 = 0,67, а другий вузол — протягом частки р

+ р

= 0,4 + 0,2 = 0,6. В такому разі перший вузол перебуває в ремонті

в середньому частку часу, що дорівнює р

+ р

= 0,2 + 0,13 = 0,33,

а другий — р

+ р

= 0,27 + 0,13 = 0,4. Тому середній прибуток за

116

одиницю часу від експлуатації системи (різниця між доходом та

витратами) буде таким:

ПРИБУТОК = 0,67 ·10 + 0,60 · 6 – 0,33 · 4 – 0,40 ·2 = 8,18 (ум. од)

Зменшення вдвічі середнього часу ремонту кожного з вузлів

згідно з

=σ=

означатиме збільшення вдвічі інтенсивності

потоку «закінчення ремонту» кожного вузла. Отже, у такому разі

=λ

і система лінійних алгебраїчних

рівнянь (1) набирає вигляду:

⎪

⎩

⎪

⎨

⎧

=+++

;427

;66

;643

3210

302

301

210

pppp

ppp

Розв’язуючи цю систему, дістаємо

,6,0

,15,0

,2,0

.05,0

Оскільки р

+ р

= 0,6 + 0,2 = 0,8; р

+ р

= 0,6 + 0,15 = 0,75,

+ р

= 0,15 + 0,05 = 0,2; р

+ р

= 0,2 + 0,05 = 0,25, то витрати на

ремонт першого та другого вузла становитимуть відповідно 8 і 4

ум. од. Звідси маємо середній прибуток за одиницю часу:

(ПРИБУТОК)

= 0,8 ·10 + 0,75 · 6 – 0,2 · 8 – 0,25 · 4 = 9,9 (ум. од.).

(ПРИБУТОК)

більший за ПРИБУТОК (наближено — на 2 %),

тому економічна доцільність скорочення термінів ремонту вузлів

очевидна.

Вправи для самостійного розв’язування

4.1.

Середня кількість літаків, які прибувають до аеропорту за

1 хв, дорівнює 3. Знайти ймовірність того, що до 2 хв прибуде:

4 літаки;

менш як 4 літаки;

не менш як 4 літаки.

Потік прибуття літаків вважається найпростішим.

4.2.

Середня кількість викликів, які надходять на АТС за 1 хв,

дорівнює 2. Знайти ймовірність того, що за 4 хв надійде:

3 виклики;

менш як 3 виклики;

не менш як 3 виклики.

Потік викликів вважається найпростішим.

117

4.3.

Середня кількість обривів ниток на ткацькому верстаті

за хвилину становить 3. Знайти ймовірність того, що за 3 хв

буде:

5 обривів ниток;

менш як 5 обривів ниток;

не менш як 5 обривів ниток.

Потік подій вважається найпростішим.

4.4.

На АТС надходить найпростіший потік викликів з інтен-

сивністю

2,1=λ

викликів за хвилину. Знайти ймовірність того,

що за дві хвилини:

не надійде жодного виклику;

надійде рівно один виклик;

надійде хоча б один виклик.

4.5.

Випадковий процес описується формулою

()

XetX

−

()

0>t

, де Х — випадкова величина, розподілена за нормальним

законом з параметрами

Знайти математичне сподівання,

дисперсію, кореляційну і нормовану кореляційну функції випад-

кового процесу.

4.6.

Побудувати граф станів такого випадкового процесу: сис-

тему утворено з двох автоматів з продажу газованої води, кожний

з яких може бути зайнятим або вільним.

4.7.

Побудувати граф станів системи

, що являє собою

електричне коло з електричною лампочкою, яка у випадковий

момент часу може бути або вимкненою, або ввімкненою, або

зіпсованою.

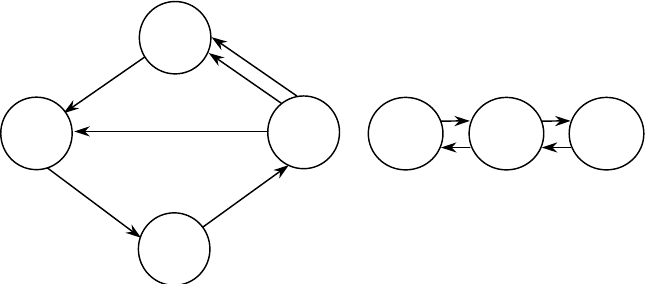
4.8.

Знайти граничні ймовірності для систем

, графи яких зо-

бражено на рис. 4.3 і 4.4.

Рис. 4.3 Рис. 4.4

118

4.9.

Середня кількість заявок на такі, що надходять на диспет-

черський пункт за 1 хв, дорівнює 3. Знайти ймовірність того, що

за дві хвилини надійде:

4 виклики;

принаймні один виклик;

не надійде жодного виклику.

4.10.

Погода на деякому острові через певні проміжки часу

стає чи дощовою (Д), чи сонячною (С). Імовірності щоденних

змін задано матрицею:

СД

6,04,0

3,07,0

⎟

⎠

⎞

⎜

⎝

⎛

=Р

Якщо в середу погода дощова, то яка ймовірність того, що

вона буде дощовою в найближчу п’ятницю?

Якщо в середу очікується дощова погода з імовірністю 0,3,

то яка ймовірність того, що вона буде дощовою в найближчу

п’ятницю?

4.11.

Імовірності переходу за один крок у ланцюгу Маркова

задано матрицею:

⎟

⎠

⎞

⎜

⎝

⎛

Потрібно: 1) знайти кількість станів; 2) побудувати граф, що

відповідає матриці Р.

4.12.

Довести, що всі стохастичні матриці виду

⎟

⎠

⎞

⎜

⎝

⎛

α−α

αα−

де

α<

мають однаковий стаціонарний розподіл.

119

Розділ 5

МАТЕМАТИЧНА СТАТИСТИКА

5.1. ПЕРВИННА ОБРОБКА І ГРАФІЧНЕ

ПОДАННЯ ВИБІРКОВИХ ДАНИХ.

ЧИСЛОВІ ХАРАКТЕРИСТИКИ ВИБІРКОВОЇ СУКУПНОСТІ

Генеральною сукупністю в математичній статистиці назива-

ється множина однотипних об’єктів, кількісна чи якісна ознака

яких підлягає вивченню. Підмножина об’єктів, дібраних у відпо-

відний спосіб із генеральної сукупності, називається вибірковою

сукупністю. Вважаємо, що ознака, яка вивчається, є випадковою

величиною Х із функцією розподілу

(

)

.xF

Результати вибірки ро-

зглядатимемо як послідовність незалежних однаково розподіле-

них випадкових величин

.,...,,

21 n

XXX

Закон розподілу для всіх

визначається функцією

(

)

.xF

Результати вибірки — реалізації

випадкових величин — позначатимемо відповідно через

xx ....,

Розмістивши ці числа в порядку зростання і записав-

ши частоти

з якими зустрічаються ці значення, дістанемо ва-

ріаційний, або статистичний, ряд:

…

Частоти

…

На підставі такого ряду можна побудувати статистичну функ-

цію розподілу

()

(

)

∑

∗

Якщо

∞

→n , то статистична фун-

кція розподілу збігається до теоретичної функції розподілу.

Статистичний ряд графічно подається полігоном розподілу.

Щоб побудувати його, на осі абсцис відкладають значення реалі-

зацій, а на осі ординат — відповідні їм частоти (відносні часто-

ти). Здобуті точки сполучають відрізками прямих.

У разі, коли Х — неперервна величина і обсяг вибірки

вели-

кий, результати вибірки подають інтервальним рядом. Для цього

область реалізацій розбивають на k інтервалів і для кожного інте-

120

рвалу визначають частоти. Кількість інтервалів nk

lg5

≤

, а їхню

довжину

x∆

найчастіше беруть однаковою. Здобутий ряд геоме-

трично подається гістограмою. Для побудови її на осі абсцис від-

кладають інтервали, а на них як на основах будують прямокутни-

ки, висота яких пропорційна до частоти (відносної частоти)

інтервалу. Гістограма дає певне уявлення про графік щільності

розподілу.

Для вибіркової сукупності обчислюють числові характеристи-

ки —

вибіркові випадкові функції: вибіркову середню

вибір-

кову дисперсію

статистичні моменти розподілу тощо. Реалі-

зації цих вибіркових функцій знаходять за формулами, вигляд

яких залежить від того, в якій формі подано вибіркові дані. Якщо

вибіркові дані не згруповано, то

()

∑∑

−==

Якщо вибіркові дані зведено у статистичний ряд, то

∑

()

∑

−=

nxx

Якщо дані подаються інтервальним рядом, то перехід до ста-

тистичного ряду виконують, обчислюючи для кожного інтервалу

його середину.

Початкові і центральні статистичні моменти розподілу обчис-

люють відповідно за такими формулами

∑

=ν

()

∑

−=µ

Формули, за якими центральні статистичні моменти подають-

ся через початкові, аналогічні тим, які виконуються для теорети-

чних моментів розподілу.

Крім того, розглядають звичайні і умовні моменти розподілу.

Звичайні моменти обчислюють за формулою

()

∑

−=

У разі подання вибіркових даних інтервальним рядом з однако-

вими довжинами інтервалів обчислення числових характеристик

значно спрощується завдяки застосуванню умовних моментів ро-

зподілу. Якщо

u — середини інтервалів і виконано заміну

∆

−

за умови, що С — одне зі значень

, то значення