Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics
Подождите немного. Документ загружается.


Variational Principles. Canonical Transformations
221
()
() ()
()
2
jjj
xt t xt xt tεΔ ε Δ ε
′′′
+= + +
O
() () ()
()
2
jjj
xt xt xt tεδ ε Δ ε=+ + + O ,
taking into account (20.1.2); using also the relations (20.1.2''), (20.1.2''') and neglecting
()
2
εO , we find again the second relation (20.1.12'').
The velocity on the varied path is given by
()()
d
d
dd
d
1...
d
ddd
1
d
jj
j
jjj
xx
x
t
xxxt
ttt
t
t
εΔ
εΔ εΔ
εΔ
+
′
′
== =+ − +
′
+
()
()
2
dd
dd
jjj
xxxt
tt
εΔ Δ ε=+ − +O .
Observing that
jj j
xx xεΔ
′
=+
and neglecting
()
2
εO , we obtain the operator
relation
dd
dd
jjj
xxxt
tt
ΔΔ Δ=−
,
(20.1.13)
which, in the asynchronous case, replaces the relation (20.1.5); this result corresponds
to
0
d
d
d
1
d
jj
j
xx
t
x
t
t
ε
εΔ
Δ
ε
εΔ
=
+
∂
=
∂
+
(20.1.13')
and can be written also in the form
d
d
jjjjj
xxxtxxt
t
ΔδΔδΔ=+=+
,
(20.1.13'')
if we take into account (20.1.5) and (20.1.12'').
By a change of variable, we may calculate the asynchronous variation of the
functional (20.1.1) in the form (
00 0
tt tεΔ
′
=+ ,
11 1
tt tεΔ
′
=+ )
()
()
1
0
12
0
, ,..., ; , d
t
n
jj
t
Ixx x Ftx x t
ε
Δ
ε
′
′
=
∂
′′ ′
=
∂
∫
()
()
1
0
0
d
;, 1 d
d
t
jjjj
t
Ft tx x x x t t
t
ε
εΔ εΔ εΔ ε Δ
ε
=
∂
⎡⎤
=++++
⎢⎥
∂
⎣⎦
∫
() ()
[]
()
{
}
1
0
0
d
1d
d
t
t
Ft Ft t t
t
ε
εΔ ε Δ
ε
=
∂
=++
∂
∫
,

MECHANICAL SYSTEMS, CLASSICAL MODELS
222
so that
()
()
1
0
12
d
, ,..., d
d
t
n
t
Ixx x F F t t
t
ΔΔΔ=+
∫
.
(20.1.14)
This relation is reduced to the relation (20.1.3'') if
0tΔ = . Further, we may write
()
1
0
12
11
d
, ,..., d
d
nn
t
n
jj
t
jj
jj
FF
Ixx x Ft x x F t t
xxt
ΔΔΔΔΔ
==
⎛⎞
∂∂
=+++
⎜⎟
∂∂
⎝⎠
∑∑
∫
1
1
1
0
0
0
11 1
d
d
d
t
t
nn n
t
jj j
t
jj j
jj j
t
t
FF F
xxFt xFFtt
xx tx
ΔΔ Δ
== =
⎛⎞⎡ ⎤
∂∂ ∂
⎛⎞
=−−+ −+
⎜⎟
⎢⎥
⎜⎟
∂∂ ∂
⎝⎠
⎝⎠⎣ ⎦
∑∑ ∑
∫
1
0
1
d
d
d
n
t
j
t
jj
j
FF
xt
xtx
Δ
=
∂∂
⎡⎛⎞⎤
+−
⎜⎟
⎢⎥
∂∂
⎣⎝⎠⎦
∑
∫
,
where we took into account the operator relation (20.1.13). But
11
dd
dd
nn
j
j
jjj
jj
FFF
xF F x
tx tx x
==
∂∂∂
⎛⎞⎡⎛⎞⎤
−+= −
⎜⎟ ⎜⎟
⎢
⎥
∂∂∂
⎝⎠⎣⎝⎠⎦
∑∑
,
and we are thus led to
()
1
0
12
11
, ,...,
t
nn
n
jj
jj
jj
t
FF
Ixx x x x F t
xx
ΔΔΔ
==
⎡
⎛⎞⎤
∂∂
=−−
⎜⎟
⎢
⎥
∂∂
⎣
⎝⎠⎦
∑∑
1
0
1
d
d
d
n
t
j
t
jj
j
FF
xt
xtx
δ
=
∂∂
⎡⎛⎞⎤
+−
⎜⎟
⎢⎥
∂∂
⎣⎝⎠⎦
∑
∫
,
(20.1.15)
on the basis of the relation (20.1.13); the second relation (20.1.12'') allows us to write
()
1
1
0
0
12
11
d
, ,..., d
d
t
nn
t
n
jj
t
jjj
jj
t
FFF
Ixx x x Ft x t
xxtx
ΔδΔ δ
==
⎡⎤
∂∂∂
⎡⎛⎞⎤
=++−
⎢⎥
⎜⎟
⎢⎥
∂∂∂
⎣⎝⎠⎦
⎣⎦
∑∑
∫
.
(20.1.15')
If the functions
j
xΔ (or
j
xδ ), 1,2,...,jn= , and tΔ vanish at the ends of the
interval (varied paths with fixed ends, for which the time is the same at both ends), it
follows
()
1
0
12
1
d
, ,..., d
d
n
t
n
j
t
jj
j
FF
Ixx x x t
xtx
Δδ
=
∂∂
⎡⎛⎞⎤
=−
⎜⎟
⎢⎥
∂∂
⎣⎝⎠⎦
∑
∫
,
(20.1.15'')
as in the synchronous case. Taking into account the constraint relations (20.1.12'') and
using Lagrange’s multipliers
k
λ , 1,2,...,km= , we may write
Variational Principles. Canonical Transformations
223
()
1
0
12
11
d
, ,..., d
d
nm
t
n
j
kkj
t
jj
jk
FF
Ixx x A x t
xtx
Δλδ
==
∂∂
⎡⎛⎞ ⎤
=−+
⎜⎟
⎢⎥
∂∂
⎣⎝⎠ ⎦
∑∑
∫
.
By the usual method, one determines the multipliers
k
λ ,
1,2,...,km=
, mn< , so
that the
m square brackets vanish; there remain nm− brackets which multiply
nm− virtual displacements, now independent. As in the synchronous case, we
prescribe the stationarity condition
()
12
, ,..., 0
n
Ixx xΔ = ;
(20.1.16)
applying the basic lemma of the variational calculus, we obtain the Euler–Lagrange
equations with multipliers
1
d
0
d
m
kkj
jj
k
FF
A
xtx
λ
=
∂∂
⎛⎞
−+=
⎜⎟
∂∂
⎝⎠
∑
, 1,2,...,jn= ,
(20.1.16')
corresponding to the true curve C. In general, in case of arbitrary asynchronous varied
curves (without fixed ends and for which the time is not the same at the ends of the
interval), we have
()
1
0
12
11
, ,...,
t
nn
n
jj
jj
jj
t
FF
Ixx x x x F t
xx
ΔΔΔ
==
⎡
⎛⎞⎤
∂∂
=−−
⎜⎟
⎢
⎥
∂∂
⎣
⎝⎠⎦
∑∑
1
0
1
t
n
j
j
j
t
F
xFt
x
δΔ
=
⎡⎤
∂
=+
⎢⎥
∂
⎣⎦
∑
(20.1.15''')
along the integral curves of the Euler–Lagrange equations with multipliers. Starting
from the relations (20.1.7) and (20.1.15''), we obtain the relation connecting the
asynchronous to the synchronous variation of a functional in the form
1
0
t
t
IIFtΔδ Δ=+ .
(20.1.17)
If
01
0ttΔΔ== (or, more general, if
() ()
01
Ft Ft= and
01
ttΔΔ= ), there
results
IIΔδ= ,
(20.1.17')
the asynchronous and synchronous variations being equal; thus, the difference between
the effects of those variations disappears.
We notice also that, in case of varied paths with fixed ends
(
() ()
01
0
jj
xt xtΔΔ==, 1,2,...,jn= ) for which 0F =
(the function
F
does not
depend explicitly on time), the Euler–Lagrange equations entail also Jacobi’s first
integral (20.1.18). The relation (20.1.15) shows that one can write
MECHANICAL SYSTEMS, CLASSICAL MODELS
224
()()
12 1 0
, ,...,
n
Ixx x h t tΔΔΔ=− −
(20.1.18)
along the integral curves of Euler–Lagrange equations; to obtain
0IΔ = , one must
have
01
ttΔΔ= , hence the motion on the varied paths must have the same duration as
on the true curve. This last condition concerning the asynchronous variations is
somewhat restrictive; we can also write
()()
12 1 0
, ,...,
n
Ixx x h t tΔΔΔ+−
() () () () () ()
()
[]
1
0
12 12
, ,..., , , ,..., ; d 0
t
nn
t
Fxtxt x txtxt x tt h tΔ=+=
∫
,
(20.1.18')
a relation which can be used in various particular cases.
We will estimate
1
11
00
0
11 1
dd
t
nn n
tt
jj j
tt
jj j
jj j
t
FF F
Ft x x F t t x
xx x
ΔΔΔΔΔ
== =
⎛⎞
∂∂ ∂
=++=
⎜⎟
∂∂ ∂
⎝⎠
∑∑ ∑
∫∫
1
1
0
0
11
d
d
d
t
nn
t
jj
t
jj
jj
t
FF
xt x F tt
xtx
ΔΔ
==
⎡⎤
∂∂
⎛⎞
−+ +
⎢⎥
⎜⎟
∂∂
⎝⎠
⎣⎦
∑∑
∫
1
0
1
d
d
d
n
t
j
t
jj
j
FF
xt
xtx
Δ
=
∂∂
⎡⎛⎞⎤
+−
⎜⎟
⎢⎥
∂∂
⎣⎝⎠⎦
∑
∫
,
using the variation (20.1.14) without the term
()
d/dFttΔ . We can write
1
1
0
0
11
d
d
d
t
nn
t
jj
t
jj
jj
t
FF
FxtFtt x
xt x
ΔΔΔΔ
==
⎛⎞
∂∂
+−=
⎜⎟
∂∂
⎝⎠
∑∑
∫
1
0
1
d
d
d
n
t
j
t
jj
j
FF
xt
xtx
Δ
=
∂∂
⎡⎛⎞⎤
+−
⎜⎟
⎢⎥
∂∂
⎣⎝⎠⎦
∑
∫
(20.1.19)
too. It follows
1
1
0
0
11
d
d
d
t
nn
t
jj
t
jj
jj
t
FF
FxtFtt x
xt x
ΔΔΔΔ
==
⎛⎞
∂∂
+−=
⎜⎟
∂∂
⎝⎠
∑∑
∫
(20.1.19')
along the integral curves of Euler–Lagrange equations. If the varied paths are with fixed
ends (
() ()
01
0
jj
xt xtΔΔ==), then we can state
Theorem 20.1.4 (O. Hölder). In the case of asynchronous varied paths with fixed ends,
the functional (20.1.1) verifies the relation
1
0
1
d
d0
d
n
t
j
t
j
j
F
FxtFtt
xt
ΔΔΔ
=
⎛⎞
∂
+−=
⎜⎟
∂
⎝⎠
∑
∫
(20.1.19'')
Variational Principles. Canonical Transformations
225
along the integral curves of the corresponding Euler–Lagrange equations.
In case of some constraint relations of the form (20.1.12), one uses, as above, the
methods of Lagrange’s multipliers.
20.1.2 The General Integral Principle
Following the ideas of the previous section, we will state the general form of a
variational principle and of the general integral principle; these results will be given for
synchronous as well as for asynchronous variations.
20.1.2.1 Preliminary Considerations
Let be a discrete mechanical system
S of n particles and
i
P
a particle of this
system, of position vector
i
r with respect to an inertial frame of reference, subjected to
the action of the resultant
i
F
of the given forces (by given forces we intend external as
well as internal ones); it is obvious that
1,2,...,in= . In the time interval
[
]
01
,tt , the
particle
i
P
describes the true curve
i
C
of equation
()
ii
t=rr
. Let us suppose that the
particle
i
P
is displaced by
i
εΔr , where ε is a small parameter, till the point
i
P
′
of
position vector
ii i
εΔ
′
=+
rr r,
1,2,...,in=
.
(20.1.20)
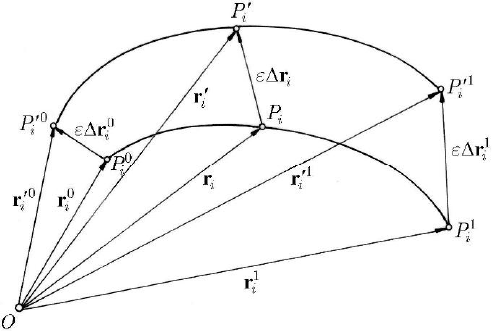
Fig. 20.2 Varied paths
From the set of possible displacements
()
i
tΔr of class
2
C , we choose those which,
univocally, lead to the point
i
P
′
, the locus of which is a varied path
i
C
′
(see Fig. 20.2);
the motion on this path corresponds to the proper time
t
′
, given by (20.1.2''). One
obtains thus an infinity of varied paths, the motion on those ones being, in general,
asynchronous (
0tΔ ≠ ). If 0tΔ = , the variations are synchronous, and
ii i
εδ
′
=+
rr r, 1,2,...,in= ,
(20.1.20')

MECHANICAL SYSTEMS, CLASSICAL MODELS
226
where
i
δr are virtual displacements (synchronous variations). We assume that the
possible displacements verify the linear constraint relations
0
1
0
n
i
ki k
i
tΔαΔ
=
⋅+ =
∑
rα
, 1,2,...,km= ,
(20.1.21)
where
()
12
, ,..., ;
n
ki ki
t= rr rαα , 1,2,...,in= , and
()
12
00
, ,..., ;
n
kk
tαα= rr r are
functions of class
1
C . Considering also the finite form of the constraint relations
0
1
0
n
i
ki k
i
α
=
⋅+ =
∑
rα
,
1,2,...,km=
,
(20.1.21')
and eliminating the parameter
0k
α , we find constraint relations of the form
1
0
n
i
ki
i
δ
=
⋅=
∑
rα
, 1,2,...,km= ,
iii
tδΔ Δ=−rrv, 1,2,...,in= ,
(20.1.21'')
where, obviously,
ii
=
vr
are real velocities, while
i
δr
are virtual displacements.
The velocity on the varied path is given by
()()
d
d
dd
d
1...
d
ddd
1
d
ii
i
iii
t
t
ttt
t
t
εΔ
εΔ εΔ
εΔ
+
′
′
== =+ − +
′
+
vr
r
vvr
()
()
2
dd
dd
iii
t
tt
εΔ Δ ε=+ − +vrvO .
We notice that
ii i
εΔ
′
=+vv v and we neglect
()
2
εO ; the asynchronous variation of
the velocity is thus given by
dd
dd
iii
t
tt
ΔΔ Δ=−vrv, 1,2,...,in= .
(20.1.22)
Because
()
d/dd/dd
iii
tt tt tΔΔ=+vva, where
i
a is the acceleration of the
particle
i
P , we can write this relation also in the form
d
d
iii
t
t
ΔδΔ=+vra, 1,2,...,in= ,
(20.1.22')
where we took into consideration the second relation (20.1.21''). If
0tΔ = , then one
obtains the synchronous variation
d
d
ii
t
δδ=
vr, 1,2,...,in= ,
(20.1.23)

Variational Principles. Canonical Transformations
227
and the operator relation (20.1.5'). Hence, the relation between the two variations
(asynchronous and synchronous) will be of the form
iii
tΔδ Δ=+vva,
d
d
i
i
t
=
v
a
, 1,2,...,in= .
(20.1.22'')
The synchronous variation of the kinetic energy will be given by
()
()
2
22 2
11
11
22
nn
ii i i i i i
ii
TTT m mεδ εδ
==
′′
=−= − = + −
⎡
⎤
⎣
⎦
∑∑
vv v v v
()
2
1
n
ii i
i
mεδε
=
=⋅+
∑
vvO ,
so that
1
n
ii i
i
Tmδδ
=
=⋅
∑
vv;
(20.1.24)
analogously, we obtain the asynchronous variation
1
n
ii i
i
TmΔΔ
=
=⋅
∑
vv
.
(20.1.24')
Performing a scalar multiplication of the relation (20.1.22'') by
ii
m v summing for all
values of the index
i , taking into account (20.1.24), (20.1.24'), and observing that
()
2
d/2/d
iii
t =⋅vva, we can write the relation between the asynchronous and the
synchronous variation of the kinetic energy in the form
d
d
T
TT t
t
Δδ Δ=+
.
(20.1.25)
In case of quasi-conservative given forces, which derive from a quasi-potential
()
12
, ,..., ;
n
UU t= rr r , we obtain the asynchronous variation
1
n
ii
i
UUUtΔΔΔ
=
=∇⋅ +
∑
r
,
U
U
t
∂
=
∂
;
(20.1.26)
the synchronous variation is of the form
1
n
ii
i
UUδδ
=
=∇⋅
∑
r .
(20.1.26')
Observing that
1
d
d
n
ii
i
U
UU
t
=
=∇⋅+
∑
v
MECHANICAL SYSTEMS, CLASSICAL MODELS
228
and taking into account the second relation (20.1.21''), one obtains the relation between
the asynchronous and the synchronous variations of the quasi-potential in the form
d
d
U
UU t
t
Δδ Δ=+
.
(20.1.27)
For the mechanical energy
ETUTV=−=+, VU=− , one obtains,
analogously,
d
d
E
EE t
t
Δδ Δ=+
,
(20.1.28)
while for Lagrange’s kinetic potential
TU TV=+=−L we can write
d
d
t
t
Δδ Δ=+
L
LL
.
(20.1.28')
Generically, we denote by E a quantity of energetic nature, e.g.,
,,,TU EL or any
other linear combination (with numerical coefficients) of them; as a matter of fact, two
of these quantities can be considered as basic ones (for instance
T
and L ), while the
other quantities are expressed by means of them. We will thus have
d
d
t
t
Δδ Δ=+
E
EE
.
(20.1.28'')
Let us introduce the functional
1
0
d
t
t
t=
∫
A E ,
(20.1.29)
called action; the quantity
dt E will be the elementary action. We have thus to do with
the kinetic action
T
A
, corresponding to T=E , with the potential action
U
A
, for
U=E , with the Lagrangian action
L
A
, corresponding to = LE , or with the
mechanical action
E
A
, for E=E . We mention that the magnitude 2
T
A
corresponds
to the classical notion of action. Using the formula (20.1.14), we can express the
asynchronous variation of the action
A
in the form
()
11
00
d
dd
d
tt
tt
ttt
t
ΔΔ Δ Δ==+
∫∫
A EEE;
(20.1.29')
analogously, the corresponding synchronous variation is given by
11
00
dd
tt
tt
ttδδ δ==
∫∫
A EE,
(20.1.29'')
where a permutation between the operator
δ and the integral operator is possible.
Taking into account (20.1.28''), we can express the asynchronous variation (20.1.29') in
the form

Variational Principles. Canonical Transformations
229
1
1
0
0
d
t
t
t
t
ttΔΔ δ=+
∫
A EE;
(20.1.30)
hence, the relation between the asynchronous and the synchronous variations of an
action is given by
1
0
t
t
tΔδ Δ=+AAE .
(20.1.30')
If
01
0ttΔΔ== (or, more general, if
() ()
01
tt=EE and
01
ttΔΔ= , the motion
having the same duration on all varied paths), we obtain
Δδ=
A
A ,
(20.1.30'')
the asynchronous variation being equal to the synchronous one.
20.1.2.2 Two Forms of a General Integral Principle
Starting from the principle of virtual work, which can be applied in case of ideal
constraints (see Sect. 11.1.2.10), written in the form
1
0
n
ii
i
δ
=
⋅=
∑
rΦ ,
ii ii
m=−FaΦ ,
(20.1.31)
where
i
F are given forces (external and internal), and integrating with respect to time,
between the limits
0
t and
1
t , we obtain
1
0
1
d0
n
t
ii
t
i
tδ
=
⋅=
∑
∫
rΦ .
(20.1.31')
Inversely, starting from (20.1.31') and using the basic lemma of Lagrange (the virtual
displacements
i
δr are independent or verify the constraint relations (20.1.21''), case in
which one uses Lagrange’s multipliers
k
λ , 1,2,...,km= , leading to the constraint
forces
1
m
i
kki
k
λ
=
=
∑
R α
,
1,2,...,in=
), we find
i
= 0Φ or
ii
+=R0Φ ,
1,2,...,in= , hence Newton’s equations of motion. The relations (20.1.31) and
(20.1.31') are thus equivalent.
We can calculate
() ()
111
000
11 1
dd
ddd
dd
nn n
ttt
ii i i i i ii i
ttt
ii i
mt m tm t
tt
δδ δ
== =
⋅= ⋅ − ⋅
∑∑ ∑
∫∫∫
ar vr v r
1 1
1 1
0 0
0 0
111
dd
tt
nnn
tt
ii i ii i ii i
tt
iii
tt
mmtmTtδδδδ
===
=⋅− ⋅=⋅−
∑∑∑
∫∫
vr vv vr
,
where we took into account (20.1.23) and (20.1.24); on the other hand

MECHANICAL SYSTEMS, CLASSICAL MODELS
230
1
n
ii
i
Wδδ
=
⋅=
∑
Fr ,
(20.1.32)
where
Wδ is the virtual work of the external and internal given forces. Finally, the
relation (20.1.31') leads to
()
1
1
0
0
1
d
n
t
t
ii i
t
t
i
WTt mδδ δ
=
+= ⋅
∑
∫
vr
;
(20.1.33)
using only asynchronous variations, one can also write
()
1
1
0
0
1
d
d2
d
t
n
t
ii i
t
i
t
T
WTP tt m Tt
t
ΔΔ Δ Δ Δ
=
⎡
⎤
⎡⎤
+−+ = ⋅−
⎢
⎥
⎢⎥
⎣⎦
⎣
⎦
∑
∫
vr ,
(20.1.33')
where we took into account (20.1.21'') and (20.1.25), where
1
n
ii
i
WWPtΔδ Δ Δ
=
=+ = ⋅
∑
Fr
(20.1.32')
is the asynchronous variation of the work of external and internal forces and where
1
d
d
n
ii
i
W
P
t
=
== ⋅
∑
Fv
(20.1.34)
is the power of the same given forces.
In case of synchronous varied paths with fixed ends, the relation takes the form
(20.1.33), hence
()
1
0
d0
t
t
WTtδδ+=
∫
,
(20.1.35)
equivalent to the relation (20.1.31'), that is to the principle of virtual work (20.1.31).
Following V. Vâlcovici, we will call this relation the general integral principle,
because – starting from (20.1.35) – we can obtain the most important variational
(integral) principles, in case of synchronous variations (Vâlcovici, V., 1969, 1973).
In the asynchronous case, we start from the relation (20.1.33') and consider
asynchronous varied paths with fixed ends, for which
01
0ttΔΔ==; we obtain thus
()
1
0
d
d0
d
t
t
T
WTP tt
t
ΔΔ Δ
⎡⎤
+−+ =
⎢⎥
⎣⎦
∫
.
(20.1.33'')
We notice that the relation (20.1.33') can be written also in the form
()
1
1
0
0
1
dd
2d
dd
t
n
t
ii i
t
i
t
T
WT PtT tt m
tt
ΔΔ Δ Δ Δ
=
⎡⎤
++ − + = ⋅
⎢⎥
⎣⎦
∑
∫
vr;
(20.1.33''')
