Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

Hamiltonian Mechanics

211

Replacing in the equation (19.2.104), we obtain

⎧⎡ ⎤ ⎫

∂

⎛⎞

′

−+ + + =−

⎨⎬

⎜⎟

⎢⎥

′

∂

⎝⎠

⎩⎣ ⎦ ⎭

∂

⎡⎤

⎛⎞

⎜⎟

⎢⎥

∂

⎝⎠

⎣⎦

222

122

sin ,

ha kMa

kI a

where

a is the third essential constant; there results thus the complete integral

′′′

=− + + +

∫∫

11 2 2

()d ()dShta RρρρΘθθ,

(19.2.105)

where we have denoted

() ( )

′′

=−−− =−

22 22 2 2

2212 2

()2 ,() 2 sinR Mha akM IakIρρΘθθ

(19.2.105')

The trajectory of the representative point

∈

P Λ is given by the equation

′

−=

′

−=−

′

∫

∫∫

11 1

()

() ()

MMa

ρΘθ

(19.2.106)

while the motion on the trajectory is specified by

′

=−

′

∫

()

Mtt

(19.2.106')

Eliminating the integral between the first equation (19.2.106) and the equation

(19.2.106'), we get

()

′

=−+

tt b

(19.2.107)

hence the projection of the mass centre on the

Ox -axis has a uniform motion. The

integral with respect to

′

ρ leads to

()

′

=−= −−=

221

cos , 2 ,

AttA Mhaa k

ρω ω

;

(19.2.107')

the constants

a and

a must verify the positiveness of the quantity under the radical

(we have

0, 0kh>> too). The integral with respect to θ is an elliptic one.

Obviously, these results correspond to those in Sect. 19.1.3.5, where one eliminates the

MECHANICAL SYSTEMS, CLASSICAL MODELS

212

generalized momenta

p and p

between (19.1.97) and (19.1.97') ( θ verifies the

equation of the mathematical pendulum); moreover, the respective formulae allow then

to calculate these generalized momenta.

Chapter 20

Variational Principles. Canonical Transformations

We will present first the main variational principles, which allow a formulation of

the motion problems of mechanical systems in the configuration space

Λ , as well as in

the phase space

. Then, we consider the canonical transformations which let

invariant the equations of motion in the space

, as well as the variational principles

from which they are deduced (their canonical form). A special attention is given to

Noether’s theorem, obtaining thus first integrals for the equations of motion.

20.1 Variational Principles

The differential principles of mechanics (with a local character) have been presented

in Sect. 6.2.1.4 for a particle and in Sect. 11.1.2.10 for a discrete mechanical system of

particles. New differential principles, in a global form, have been introduced in Sects.

12.1.1.2 and 20.1.2 for continuous mechanical systems and in Sects. 14.1.1.10 and

20.1.2.1 for the free rigid solid and for the rigid solid with constraints, respectively. In

Sect. 18. the principles of Newton, d’Alembert, Gauss and Hertz are stated in the space

E , as well as various forms of the principle of virtual work (d’Alembert-Lagrange,

Jourdain, Gauss a.s.o.) in the space

(Newton, I., 1686–1687; Alembert d’, 1743;

Hertz, H., 1894).

Unlike the differential principles, the variational principles of mechanics have a

global character – being integral principles; they do not reply to certain causality

conditions and do not correspond to an actual (present) state of the mechanical system,

but contain in them the past as well the future of this one. In connection with the

variational principles, we can mention the names of W.R. Hamilton, M.V.

Ostrogradskiĭ, J.-L. Lagrange, P.-L. Moreau de Maupertuis, K.-G.-J. Jacobi, O. Hölder,

A. Voss etc (Hamilton, W.R., 1890; Ostrogradskiĭ, M.V., 1946; Lagrange, J.-L., 1788;

Jacobi, C.G.J., 1882; Voss, A., 1901).

We notice that the basic principles of Newtonian mechanics (see Sect. 1.1.2.5) have

a physical, mechanical meaning, their formulation being thus adequate. In the frame of

Lagrangian and of Hamiltonian mechanics we are led to an analytical formulation of

those principles, with a tendency of universality, even if we are situated – sometimes –

in the frame of particular mechanical systems; obviously, this analytical formulation has

also a pregnant mechanical substratum, even this one is not evident from the very

beginning. The analytical principles of mechanics try, in general, to contain – besides

the laws of Newtonian mechanics – also other natural laws (corresponding to a thermal

213

P.P. Teodorescu, Mechanical Systems, Classical Models,

MECHANICAL SYSTEMS, CLASSICAL MODELS

214

or electromagnetic field, or to some optical and acoustical phenomena a.s.o.); in fact,

this is one of the tendencies of actual physics: unification of mechanical and physical

phenomena in a unitary analytical formulation. The model used for these formulations

is that of Fermat’s principle, governing geometrical optics, the variational method of

calculus being essential.

These analytical principles can have a differential character (as the principle of

virtual work) or an integral character; in the last case, we study the behaviour of the

mechanical system as a whole. We apply certain variations to the trajectories of the

particles which constitute the mechanical system (or to the trajectory of the

representative point), defining thus varied (admissible) paths; to a point on the true

(real) trajectory will correspond, univocally, a point on the varied path. If the

chronology of the motion is the same on both trajectories, then the variation is

synchronous; otherwise, it is asynchronous.

We pass in review some results having a general character (from a mathematical point of

view, as well as concerning variational principles). We present then Hamilton’s and

Maupertuis’s principles, and some applications of them to continuous mechanical systems;

we consider also other variational principles in the frame of a general theory.

20.1.1 Mathematical Preliminaries

We present in what follows some preliminaries having a mathematical character,

concerning variational calculus, useful for the general form which can have the

corresponding principles; the synchronous form as well as the asynchronous form can

be put thus into evidence.

20.1.1.1 General Considerations

In Sect. 7.2.1.4 we have made concise considerations concerning equations leading

to the extremal curves in case of some particular functionals. In case of variational

principles of mechanics, we take again the problem for the functionals of the form

()

() () () () () ()

()

12 12 12

, ,..., ; , ,..., , , ,..., d

nnn

Ixx x Ftxtxt xtxtxt xt t≡

∫

 

(20.1.1)

where

()

xxt= , 1,2,...,

n= , are the parametric equations of a curve C in

\ ;

the co-ordinates

x can be, in particular, the co-ordinates of a particle in

E , the co-

ordinates of a discrete mechanical system in

E , or the co-ordinates of a

representative point in

or in

Γ . Corresponding to the definition of a functional, to

every point P of C corresponds a real number

()

, ,...,

Ixx x , by the integral

(20.1.1); we admit that the functions

()

xt are of class

C on the interval

[

]

,tt , the

function

being also of class

with respect to its arguments. In the basic problem

one must determine the functions

()

xt for which

realizes an extremum (maximum

or minimum).

By convention, the geometric image of the functions

()

xt is called a real (true)

curve C; starting from the point P of the curve C, we will define the point

′

, hence

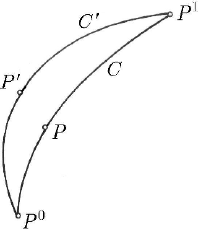
Variational Principles. Canonical Transformations

215

the varied path

′

, using functions of the form

()

;

xxtε

′′

= ,

[

]

,ttt∈ , of class

, the parameter ε varying in an interval containing the origin. We suppose that,

along these varied paths, the conditions imposed in the problem, corresponding to the

real (natural) curve, are not violated; if the latter one is obtained for

0ε = , then we

take

()

xt xt

′

= , so that

() () ()

jj j

xt xt xtεδ

′

=+ ,

1,2,...,

(20.1.2)

where the variations

()

xtδ are functions of class

C , while ε is a small parameter. It

is convenient to assume that all varied paths

′

are with fixed ends (they have the same

origin

P and the same extremity

P (

() ()

xt xt

′

() ()

xt xt

′

) (see

Fig. 20.1); hence,

() ()

xt xtδδ==, 1,2,...,

n= .

(20.1.2')

If the points

P and P

′

are in motion on the curve C and on the path C

′

respectively, with the same chronology (the same time

t ), we say that we have to do

with a synchronous variation (denoted by

xδ ); otherwise, the variation is

asynchronous (denoted by

xΔ

), the corresponding chronology being specified by the

time variable

Fig. 20.1 Varied paths with fixed ends

tt tεΔ

′

=+ ,

(20.1.2'')

where

tΔ is a function of class

C , of time t ; we can write

()

() ()

jj j

xt xt xtεΔ

′′

, 1,2,...,jn= .

(20.1.2''')

Obviously, for

0tΔ = we obtain a synchronous variation.

20.1.1.2 Case of Synchronous Variations

Introducing the variation of the function

F , we can write

()

′′

Ftx x



()

Ftx x Fεδ=+



in case of a synchronous variation; but a development into a

Taylor series allows us to write

MECHANICAL SYSTEMS, CLASSICAL MODELS

216

()()

()

;, ;,

jj jj j j

Ftx x Ftx x x x

εδ δ ε

∂∂

⎛⎞

′′

=+ ++

⎜⎟

∂∂

⎝⎠

∑

 



so that, using both expressions, we obtain

()

FFtxx

∂

′′

∂



(20.1.3)

It results also

()

12 12

, ,..., , ,...,

Ixxx Ixxx

∂

′′ ′

∂

(20.1.3')

Observing that

()

() ()

()

∫

, ,..., ; , d

Ixx x Ftx t x t tδδ



() ()

()

∂

′′

∂

∫

;, d

Ftx t x t t



() ()

()

∂

′′

∂

∫

;, d

Ftxtxt t



we have

()

() ()

()

, ,..., ; , d

Ixx x Ftxtxt tδδ=

∫



(20.1.3'')

If the functional

()

, ,...,

Ixx x has an extremum, then the function

()

, ,...,

Ix x x

′′ ′

, considered to be a function of the parameter ε (denoted ()f ε ),

takes an extreme value for

0ε = . If (0)f is an extremum, then – necessarily –

()

(0) , ,..., / 0

fIxxx

′′′′

=∂ ∂ =

for any variation

xδ ; taking into account

(20.1.3'), there results

()

, ,..., 0

Ixx xδ = .

(20.1.4)

We can thus state

Theorem 20.1.1 If the functional

()

, ,...,

Ixx x has an extremum for

()

xxt= ,

then – necessarily – the relation (20.1.4) takes place for any virtual variation

xδ ,

1,2,...,

, of the accepted class (20.1.2).

If the condition (20.1.4) is verified, then we will say – by definition – that the

functional

()

, ,...,

Ixx x is stationary on the varied paths obtained starting from the

functions

()

xxt= , 1,2,...,jn= .

To can associate a sufficient condition of extremum, one takes into account also the

variation of second order

()

222

12 12

, ,..., , ,..., /

Ixx x Ix x x

δε

′′ ′

=∂ ∂

. One can

Variational Principles. Canonical Transformations

217

prove that to realize a maximum or a minimum for the functional

()

, ,...,

Ixx x it is

sufficient to have

()

, ,..., 0

Ixx xδ < or,

()

, ,..., 0

Ixx xδ > , respectively, for

any variation

()

xtδ , 1,2,...,jn= .

If we differentiate the relation (20.1.2) with respect to time, then we obtain

d/d

jj j

xx xtεδ

′



, so that

δδ=



;

(20.1.5)

there results the operator relation

ddtt

δδ=

(20.1.5')

which takes place only in case of synchronous variations. This permutability relation is

replaced by a transitivity relation (

dd 0δδ−≠) in case of asynchronous variations.

Let

()

ft be a continuous function on the interval

[

]

,tt , with real values. One

supposes that there exists

()

,ttτ ∈ , so that () 0f τ ≠ (to fix the ideas, () 0f τ > );

there exists an interval

()

[

]

01 01

,,ttττ ⊂ for which

()

,τττ∈ , and

()

0ft > if

[

]

,t ττ∈ . Let also be a function

()

tη

of class

C on the interval

[

]

,tt , with

real values, defined by

()

0 for ,

for ,

0 for .

tt t t

ηττ ττ

≤<

⎧

⎪

=− − ≤≤

⎨

⎪

<≤

⎪

⎩

We have

()() ()

()

dd0

ft t t ft t t t

ηττ=−−>

∫∫

;

by reducing ad absurdum, we can state

Theorem 20.1.2 (the basic lemma of variational calculus; J.-L. Lagrange). Let

[

]

→

:,ftt

be a continuous function. If

()()

ft t tη =

∫

(20.1.6)

for any function η

[

]

→

:,tt

of class

C , vanishing at the ends of the interval

(

() ()

0ttηη==), then

()

0ft =

on the interval

[

]

,tt .

This result takes place also for

Cη ∈ .

In case of synchronous variations, the relation (20.1.3'') leads to

MECHANICAL SYSTEMS, CLASSICAL MODELS

218

()

, ,..., d

Ixx x x x t

δδδ

∂∂

⎛⎞

⎜⎟

∂∂

⎝⎠

∑

∫



while the relation (20.1.5) allows to write (integration by parts)

()

, ,..., d

jjj

FFF

Ixx x x x t

xxtx

δδ δ

∂∂∂

⎡⎛⎞⎤

=+−

⎜⎟

⎢⎥

∂∂∂

⎣⎝⎠⎦

∑∑

∫



;

(20.1.7)

taking into account the conditions (20.1.2'), there results

()

, ,..., d

Ixx x x t

xtx

δδ

∂∂

⎡⎛⎞⎤

=−

⎜⎟

⎢⎥

∂∂

⎣⎝⎠⎦

∑

∫



(20.1.7')

Imposing the stationarity condition (20.1.4), taking a non-zero variation

xδ (all

other variations vanishing), and using the basic lemma of the variational calculus, we

can show that the parenthesis multiplying

xδ must vanish; using this reasoning for any

1,2,...,jn= , we obtain the Euler–Lagrange equations (denomination which puts in

evidence the contribution of Euler (1744) and of Lagrange (1760) to the development

of variational calculus) (Euler, L., 1955–1974)

xtx

∂∂

⎛⎞

−=

⎜⎟

∂∂

⎝⎠



, 1,2,...,jn= .

(20.1.7'')

Corresponding to the results in Sect. 18.2.3.4, we notice that for

0F =



these equations

admit the Jacobi’s first integral

xFh

∂

−=

∂

∑



(20.1.8)

where

is an integration constant.

In general, we observe that in case of arbitrary synchronous varied paths (without

fixed ends), we have

()

, ,...,

Ixx x x

δδ

∂

∑



(20.1.7''')

along the integral curves of Euler–Lagrange equations.

The problem of a brachistochrone curve, formulated by J. Bernoulli in 1696 and

studied in Sect. 7.2.1.5, is the first problem of a variational nature which has been

considered.

20.1.1.3 Case of Functionals Which Depend on Functions of Several Variables

The results obtained above can be used successfully in case of discrete mechanical

systems. To study continuous mechanical systems one must introduce a functional of

the form

Variational Principles. Canonical Transformations

219

() d

Iu Ft=

∫

(20.1.9)

where

()

123 123

;,,,,,,, dFtxxxuuuuu

Ω

Ω=

∫

F ,

(20.1.9')

()

123

,,;uuxxxt= being a function of class

C . Here Ω is a three-dimensional

domain (eventually the support of a continuous mechanical system), which can be also

two- or one-dimensional,

123

ddddxxxΩ = is the support element, while F is a

density (corresponding to the unit of support); one has denoted

/uut=∂ ∂



uux=∂ ∂ , 1, 2,3i = . Passing to a varied path, we introduce the admissible

functions

()()()

123 123 123

,,; ,,; ,,;uxxxt uxxxt uxxxtδ

′

=+ , where uδ are

functions of class

C , vanishing on the space frontier Ω∂ , as well as on the time one

. As in the previously considered synchronous case, we admit that the

independent variables

123

,,xxx, and

as well as their limits do not have variations.

As in the previously subsection, we can prove

Theorem 20.1.3 (the second basic lemma of the variational calculus). Let be a function

()

123

,,fxx x , continuous on the domain Ω and with real values. If

()()

∫

123 123

,, ,, d 0fxx x xx x

Ω

ηΩ

(20.1.10)

for any function

η of class

C , vanishing on Ω , then

()

123

,, 0fxx x = on the

domain

Ω .

This result is valid also for

Cη ∈ .

Expanding into a Taylor series, we can write (we use permutability relations of the

form (20.1.5'))

uu u

uutux

δδ δ δ

∂∂∂∂∂

=+ +

∂∂∂∂∂



FF F

where a summation convention from 1 to 3 is used. We notice that

()

ut u ut

ut u t u

δδ δ

∂∂ ∂ ∂∂

⎛⎞

=−

⎜⎟

∂∂ ∂ ∂ ∂

⎝⎠

∫∫

 

FF F

()

ddd

ii i i i i

uu u

ux xu xu

ΩΩΩ

δΩ δ Ω δΩ

∂∂ ∂∂ ∂∂

⎛⎞ ⎛⎞

=−

⎜⎟ ⎜⎟

∂∂ ∂∂ ∂∂

⎝⎠ ⎝⎠

∫∫∫

FFF

If we apply a formula of flux-divergence type (see App., Subsec. 2.3.3) to the first

integral in the second member of the second relation and if we notice that

uuu

Ω

δδδ

∂

===

, then, finally, it follows

MECHANICAL SYSTEMS, CLASSICAL MODELS

220

ddd dd

It t ut

utu xu

Ω

δδ δΩ δΩ

∂∂ ∂

⎡⎛⎞⎤

⎛⎞

== = − −

⎜⎟

⎢⎥

∂∂ ∂

⎝⎠

⎣⎝⎠⎦

∫∫∫ ∫∫



FF F

;

we have introduced the derivatives

d/dt and d/d

x ,

1,2, 3i =

, to notice that the

differentiation is made taking into account the implicit dependence (by the agency of

the function

u ) of F on the independent variables

123

,,,xxxt.

Applying the second basic lemma of the variational calculus and by a reasoning

similar to that of the previous subsection, we obtain the Euler–Ostrogradskiĭ equations

in the form

utu xu

∂∂ ∂

⎛⎞ ⎛⎞

−− =

⎜⎟ ⎜⎟

∂∂ ∂

⎝⎠ ⎝⎠



FF F

(20.1.11)

Obviously, in case of a n-dimensional domain one obtains a similar result

(summation from 1 to n). Also, in case of several dependent functions

1,2,...,mα = , there result the equations

utu xu

αα α

∂∂ ∂

⎛⎞

−− =

⎜⎟

∂∂ ∂

⎝⎠



FF F

, 1,2,...,mα = .

(20.1.11')

20.1.1.4 Case of Asynchronous Variations

We suppose that the variations which lead from the motion on the true curve to the

motion on a varied path are such that the two motions are not synchronous; we will thus

consider the functional (20.1.1), using the notations introduced in Sect. 20.1.1.1 for

asynchronous variations. The quantities

()

xtΔ play the rôle of possible

displacements, of class

C , which satisfy linear constraint relations of the form

kj k

Ax A tΔΔ

∑

, 1,2,...,km= ,

(20.1.12)

where

()

, ,..., ;

kj kj

AAxx xt= , 1,2,...,

n= , and

()

, ,..., ;

AAxxxt=

are functions of class

. We consider also the finite form of these relations

kj k

Ax A

∑



, 1,2,...,km= ;

(20.1.12')

eliminating the parameter

A , we find constraint relations of the form

Axδ

∑

, 1,2,...,km= ,

jjj

xxxtδΔ Δ=−



, 1,2,...,jn= ,

(20.1.12'')

where

xδ are virtual displacements. We notice that, expanding into a Taylor series,

one can write