Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics
Подождите немного. Документ загружается.


Hamiltonian Mechanics
191
Remaking the modality to pass from Lagrange’s equations to the canonical ones
(Legendre’s transformation), we obtain
∂∂
==−=−
∂∂
,,
jj
jj
SW
qSpWSW
qq
.
(19.2.69'')
We can write, as well,
∂∂
=−
∂∂
j
j
SW
aa
,
(19.2.70)
being thus led to the above results.
Obviously, the modality to approach the problem is equivalent to the previous one,
that we can make an analogous study concerning the possibility to separate the
variables.
19.2.3 Applications
First of all, we will consider the case of motion of a single particle; we pass then to
the application of the Hamilton–Jacobi method in case of a system of two particles, as
well as in case of a rigid solid.
19.2.3.1 Motion of a Particle
The canonical co-ordinates are
==,, 1,2,3
jjj
qxpj in case of a free particle
123
(,, )Px x x (see Sect. 19.1.3.1); the Hamilton-Jacobi equation, which corresponds to
the Hamiltonian (19.1.79'), reads
()
⎡⎤
∂∂∂
⎛⎞⎛⎞⎛⎞
+++=+
⎜⎟⎜⎟⎜⎟
⎢⎥
∂∂∂
⎝⎠⎝⎠⎝⎠
⎣⎦
222
123
1
2
2
SSS
SmUh
mx x x
.
(19.2.71)
Assuming that the quasi-potential
U is a potential ( = 0U
), we can take
=− +
123
(,, )ShtSxxx,
h
being the energy constant; the reduced Hamilton–Jacobi
equation reads
()
()
∂∂∂
⎛⎞⎛⎞⎛⎞
=++=+
⎜⎟⎜⎟⎜⎟
∂∂∂
⎝⎠⎝⎠⎝⎠
222
2
123
grad 2
SSS
SmUh
xxx
.
(19.2.71')
If
=− +
12312
(,, ;,,)ShtSxxxaah is a complete integral, then we obtain the
sequences of relations
∂∂∂
===+
∂∂ ∂
12 3
12
,,
SSS
bbtb
aa h
,
(19.2.72)
∂∂∂
===
∂∂∂
123
123
,,
SSS
ppp
xxx
.
(19.2.72')

MECHANICAL SYSTEMS, CLASSICAL MODELS
192
The first two equations of the sequence (19.2.67) specify the trajectory of the
representative point
∈
3
P Λ , while the last equation gives the motion on this trajectory;
the sequence of relations (19.2.67') completes the solution for the representative point
∈
6
P Γ . If we take into account (19.1.79), we obtain the components of the velocity
(we have
===pvgrad gradSSm)
∂∂∂
===
∂∂∂
12 3
123
111
,,
SSS
xxx
mx mx mx
,
(19.2.72'')
the reduced Hamilton–Jacobi equation corresponding to the first integral of the
mechanical energy. We notice that, at each point, the velocity
v , of components
=,1,2,3
j
xj , is normal to the wave surface =
123
(,, ) constSx x x ; hence, the
trajectory of the representative point is normal to this surface.
If we make the change of function
= lnSKψ in the reduced Hamilton–Jacobi
equation (19.2.71'), then it results
()
()
−+ =
2
2
2
grad 0
2
K
Uh
m
ψψ,
(19.2.71'')
getting thus a first form of Schrödinger’s equations. This result has been obtained in the
frame of the research made to establish a differential equation from which must result
the energetical levels of the electron of the atom of hydrogen; one takes
=
2
/Uer,
where
,,meh are the mass. the charge and the energy of the electron, respectively, and
r is the distance electron-nucleus.
Starting from the Hamilton function (19.1.80'), one obtains the Hamilton–Jacobi
equation
() ()()
∂∂∂
⎡⎤
=++−=
⎢⎥
∂∂∂
⎣⎦
222
2
11
(,,;) 0
2
SSS
SUrzt
mr z
r
θ
θ
(19.2.73)
in cylindrical co-ordinates (
===
123
,,qrq qzθ ); as well, if = 0U
, then we have
=− + (,,)ShtSrzθ , the reduced Hamilton–Jacobi equation being given by
∂∂∂
⎛⎞ ⎛⎞⎛⎞
++=+
⎜⎟ ⎜⎟⎜⎟
∂∂∂
⎝⎠ ⎝⎠⎝⎠
222
2
1
2( )
SSS
mU h
rz
r
θ
.
(19.2.73')
A complete integral is
=− +
12
(,,; , ,)ShtSrzaahθ ; we can write a sequence of
relations of the form (19.2.72), as well as the sequence
∂∂∂
===
∂∂∂
,,
rz
SSS
ppp
rz
θ
θ
.
(19.2.74)
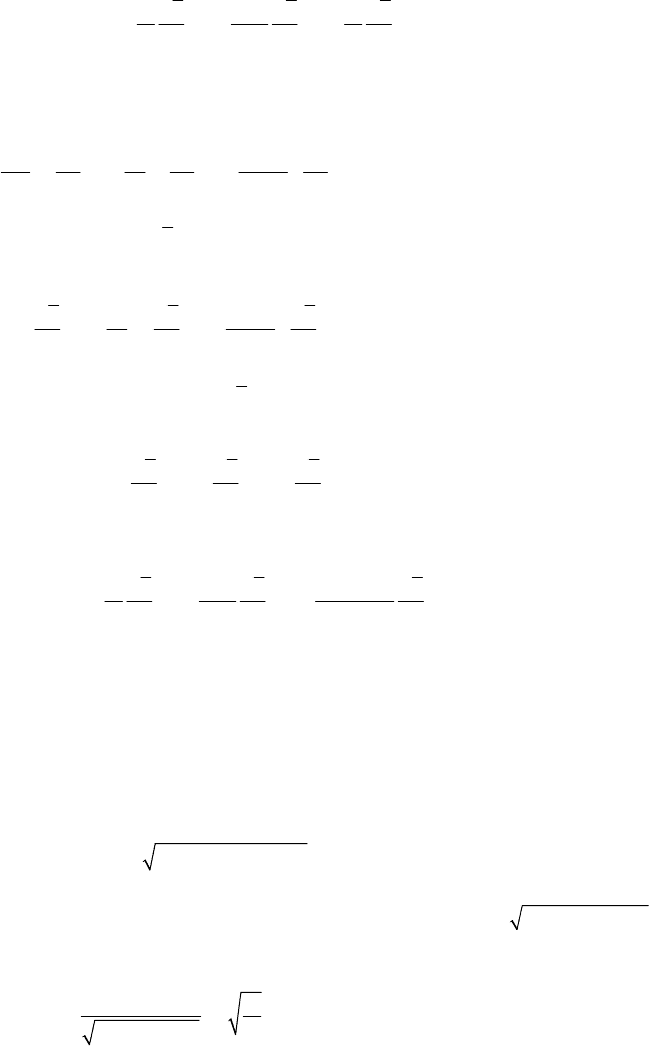
Hamiltonian Mechanics
193
The components of the velocity will be
∂∂∂
== =
∂∂∂
2
111
,,
SSS
rz
mr mz
mr
θ
θ
.
(19.2.74')
As well, in spherical co-ordinates (
===
123
,,qrq qθϕ) we obtain the Hamilton–
Jacobi equation
() ()
⎧⎡ ⎤⎫
∂∂ ∂
⎛⎞
+++ −=
⎨⎬
⎜⎟
⎢⎥
∂∂ ∂
⎝⎠
⎩⎣ ⎦⎭
2
22
22
11 1
(,, ;) 0
2
sin
SS S
SUrt
mr
r
θϕ
θϕ
θ
.
(19.2.75)
We can take
=− + (,,)ShtSrzθ if = 0U
; it results the reduced Hamilton–Jacobi
equation
⎡⎤
∂∂ ∂
⎛⎞ ⎛⎞ ⎛⎞
++ =+
⎢⎥
⎜⎟ ⎜⎟ ⎜⎟
∂∂ ∂
⎝⎠ ⎝⎠ ⎝⎠
⎣⎦
22 2
22
11
2( )
sin
SS S
mU h
r
r
θϕ
θ
.
(19.2.75')
The complete integral
=− +
12
(,, ; , , )ShtSr aahθϕ leads to a sequence of the form
(19.2.72) , to the sequence
∂∂∂
===
∂∂∂
,,
r
SSS
ppp
r
ϕ
θ
θϕ
(19.2.76)
and to the components of the velocity
∂∂ ∂
== =
∂∂ ∂
222
11 1
,,
sin
SS S
r
mr
mr mr
θϕ
θϕ
θ
.
(19.2.76')
If
=++
123 11 22 3 3
(,, ) () () ()Ux x x U x U x U x ,
(19.2.77)
then the reduced Hamilton–Jacobi equation (19.2.71') correspond to a Hamilton’s
function of the form (19.2.44), hence being with separate variables. We notice that
2
(, ) /2 , 1,2,3
jjj j j j
gxp p mU a j=−==; there result the generalized momenta
[
]
=+=2(),1,2,3
jjjj
pmUxaj .
(19.2.77')
Because
=++
123 1 2 3
(,, )Ha a a a a a, while
∂∂= = +//2()/
jjj jj
gppm Uam
,
the co-ordinates
123
,,xxx are given by (19.2.45'); we have
()
=+=
+
∫
d
2
,1,2,3
()
j
j
jj j
x
tb j
m
Ux a
,
(19.2.77'')
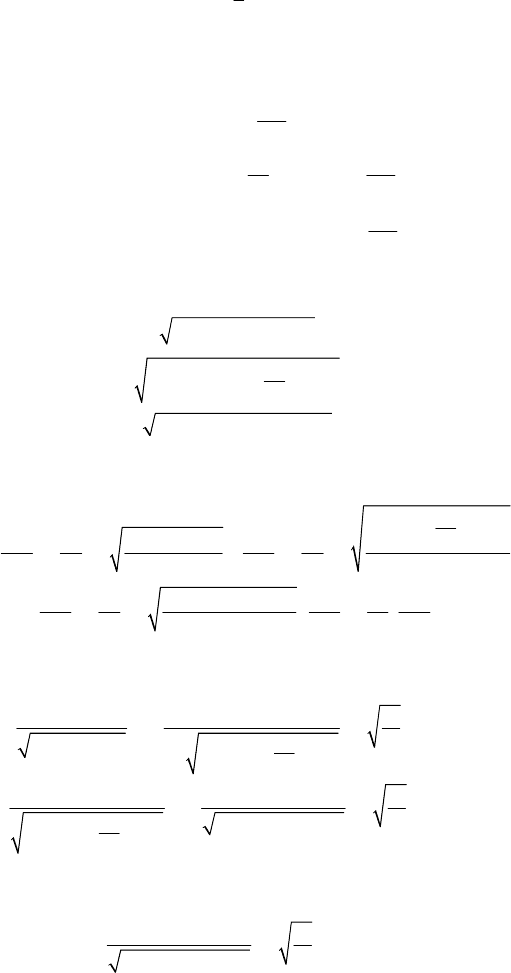
MECHANICAL SYSTEMS, CLASSICAL MODELS
194
the problem being thus reduced to three quadratures. Obviously, Hamilton’s first
equations (19.2.79'') lead to the same result.
If
=+ +
1
(,,) () () ()
2
rz
Ur z U r U U z
θ
θθ,
(19.2.78)
then Hamilton’s function (19.1.80') is of the form (19.2.46), with
==−=
==−+=
== =− + ==
2
1
2
2
2
2
3
(, ) () ,
2
(;, ) () ,
2
(;, ) () .
2
r
rr r r
z
zzrz rz
p
ggp U a
m
g
p
gggrp Ur a
m
r
p
Hg ggzp gUz a h
m
θ
θθ θ θ
θ
θ
θθ
One obtains the generalized momenta
[
]
[]
=+
⎡
⎤
=−+
⎢
⎥
⎣
⎦
=+−
1
2
2
2
2(),
2() ,
2() .
j
rr
zz
pmUa
a
pmUr a
r
pmUzha
θθ
θ
(19.2.78')
Taking into account the partial derivatives
()
(
)
()
−+
∂+
∂
== ==
∂∂
+−
∂∂∂
== = =
∂∂∂
1
2
2
1
2
2
12
2
2
,,
2
1
,,1,
r
rr
r
z
zz r z
z
a
Ua
gp Ua
gp
r
pm m pm m
Uha
gp g g
pm m a a
r
θθ θ
θ
the formulae (19.2.47') give the trajectory of the particle
P in the form
−=
+
−+
−=
+−
−+
∫∫
∫∫
1
1
2
2
2
2
1
2
2
2
dd2
,
()
()
dd2
,
()
()
j
r
z
r
r
b
a
m
Ua
rUr a
r
rz
b
a
m
Uz h a
Ur a
r
θ
θ
θ
(19.2.78'')
while the formula (19.2.47'') specifies the motion on this trajectory by the equation
=
+−
∫
2
2
d2
()
z
z
b
m
Uz h a
.
(19.2.78''')
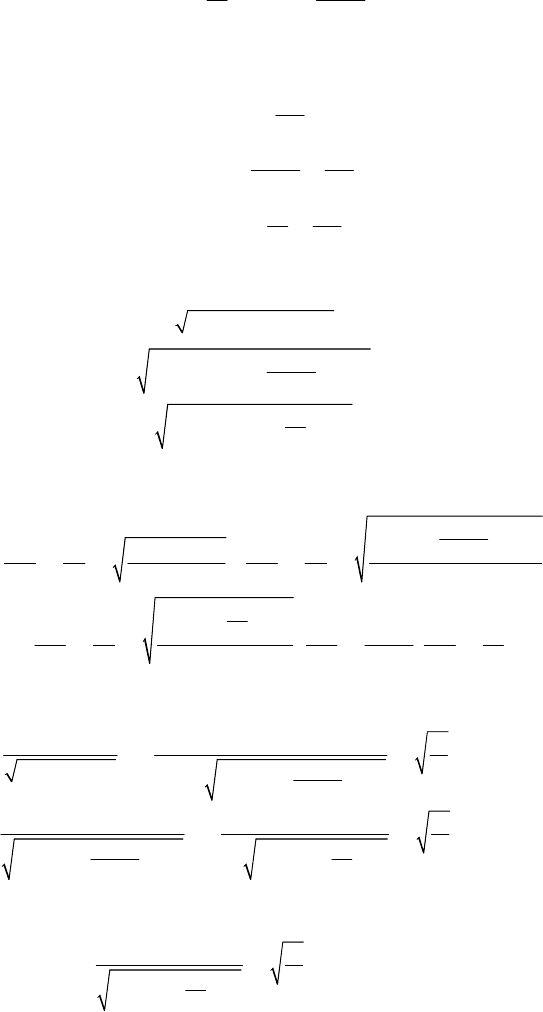
Hamiltonian Mechanics
195
The problem is thus reduced to quadratures.
In case of a potential of the form (corresponding to the potential (18.3.46))
⎡
⎤
=+ +
⎢
⎥
⎣
⎦
22
11
(,, ) () () ( )
sin
r
Ur U r U U
r
ϕ
θ
θϕ θ ϕ
θ
,
(19.2.79)
Hamilton’s function (19.1.81') is of the form (19.2.46) too, with
==−=
==+−=
== =+ − ==
2
1
2
2
2
2
3
2
(, ) () ,
2
(;,) () ,
2
sin
(;, ) () .
2
r
rr r r
p
gg p U a
m
p
g
ggg p U a
m
g
p
Hg ggrp Ur a h
m
r
ϕ
ϕϕ ϕ ϕ
ϕ
θ
ϕ
θθ θ θ
θ
θ
ϕϕ
θθ
θ
The generalized momenta will be
[]
=+
⎡
⎤
=−+
⎢
⎥
⎣
⎦
⎡
⎤
=++
⎢
⎥
⎣
⎦
1
1
2
2
2
2
2(),
2() ,
sin
2() .
rr
pmUa
a
pmU a
a
pmUr h
r
ϕϕ
θθ
ϕ
θ
θ
(19.2.79')
We calculate the partial derivatives
()
(
)
(
)
−+
∂+∂
== ==
∂∂
−+
∂
∂∂
== = =
∂∂∂
1
2
2
1
2
2
22
12
2
2
sin
,,
2
11
,,.
sin
r
rr r
r
a
Ua
gp Ua gp
pm m pm m
a
Uh
g
gp g
r
pm m a a
r
θ
θθ θ θθ
θθ
θ
θ
θ
As in the preceding case, the trajectory of the particle will be given by
−=
+
−+
−=
−+ −+
∫∫
∫∫
1
1
2
1
2
2
2
12
2
2
22
dd2
,
()
sin ( )
sin
dd2
,
() ()
sin
r
b
a
m
Ua
Ua
r
b
aa
m
UarUrh
r
ϕ
θ
θ
ϕθ
ϕ
θθ
θ
θ
θ
θ
(19.2.79'')
the motion on this trajectory being specifies by
()
=+
−+
∫
3
2
2
d2
()
r
r
tb
a
m
Ur h
r
.
(19.2.79''')
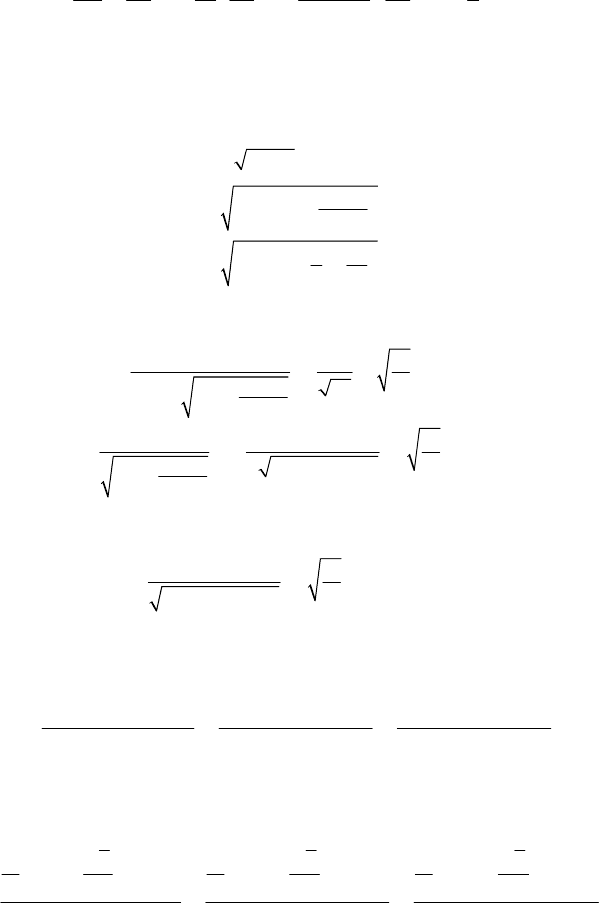
MECHANICAL SYSTEMS, CLASSICAL MODELS
196
In this case too, the problem is reduced to quadratures.
If
=>/, 0Ukrr (case of forces of Newtonian attraction), then Hamilton’s
function is given by (19.1.81') and the Hamilton–Jacobi equation reads
() ()
⎡⎤
∂∂ ∂
⎛⎞
+++ −=
⎜⎟
⎢⎥
∂∂ ∂
⎝⎠
⎣⎦
2
22
222
11 1
0
2
sin
SS Sk
S
mr r
rr
θϕ
θ
.
(19.2.80)
As a matter of fact, this case is contained in the previously considered one. The
generalized momenta will be (
== =0, /
r
UU Ukr
ϕ
θ
, while ϕ is a cyclic
co-ordinate)
()
()
==
=−
=+−
1
1
2
2
2
2
2const,
2,
sin
2.
r
pma
a
pma
a
k
pmh
r
r
ϕ
θ
θ
(19.2.80')
The trajectory of the particle is given by
=−
−
−=
+−
−
∫
∫∫
1
1
2
1
2
2
2
1
2
2
2
d2
,
sin
sin
dd2
,
sin
b
a
am
a
r
b
a
m
rhr kr a
a
ϕθ
θ
θ
θ
θ
(19.2.80'')
the motion on this trajectory being specified by
()
=+
+−
∫
3
2
2
d2rr
tb
m
hr kr a
.
(19.2.80''')
In the case of elliptic co-ordinates (see Sects. 18.3.2.1 and 19.1.3.1) let us suppose
that the simple potential
U is given by
=++
−− −− −−
11 22 33
1213 2321 3132
() () ()
()()()()()()
Uq Uq Uq
U
qqqq qqqq qqqq
.
(19.2.81)
Taking into account Hamilton’s function (19.1.83) and the notations (18.2.37'),
(18.3.39'), we can write the reduced Hamilton-Jacobi equation in the form
∂∂∂
⎛⎞ ⎛⎞ ⎛⎞
−−−
⎜⎟ ⎜⎟ ⎜⎟
∂∂∂
⎝⎠ ⎝⎠ ⎝⎠
++=
−− −− −−
22 2
112 23 3
12 3
1213 2321 3132
22 2
() () ()
()()()()()()
SSS
fq U fq U fq U
mq mq mq
h
qqqq qqqq qqqq
.
The identity
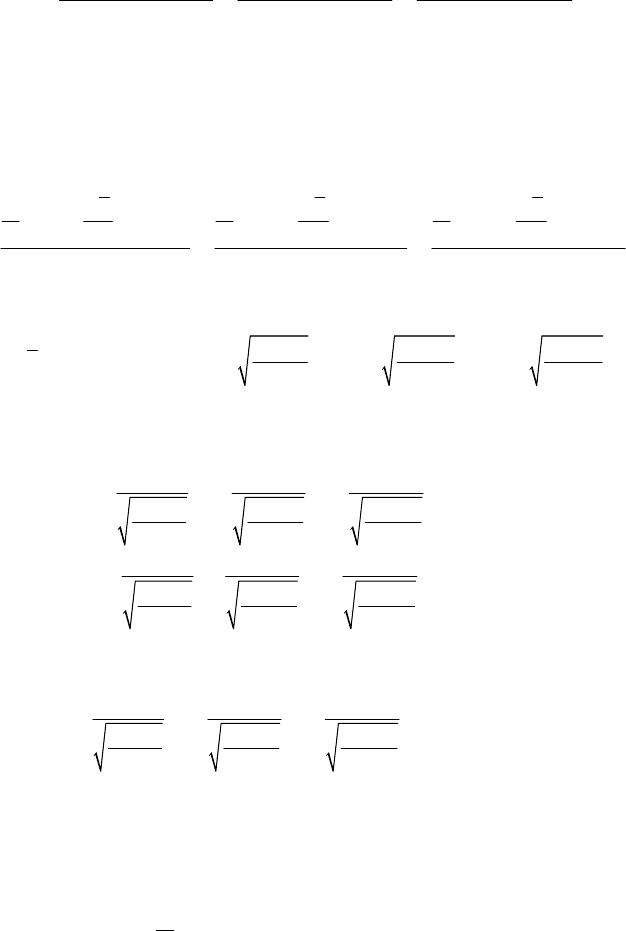
Hamiltonian Mechanics
197
++ ++ ++
++=
−− −− −−
222
1211 1222 1233
1213 2321 3132
22 22 22
()()()()()()
aaqhq aaqhq aaqhq
h
qqqq qqqq qqqq
is easily verified for any
1
a and
2
a ; denoting
=+ + =
2
12
2()2 2 , 1,2,3
jj j j
Sq a aq hq j ,
(19.2.82)
the Hamilton–Jacobi equation takes the form
∂∂∂
⎛⎞ ⎛⎞ ⎛⎞
−−−
⎜⎟ ⎜⎟ ⎜⎟
∂∂∂
⎝⎠ ⎝⎠ ⎝⎠
++=
−− −− −−
222
112 23 3
12 3
1213 2321 3132
22 2
() 2 () 2 () 2
0
( )( ) ( )( ) ( )( )
SSS
fq S fq S fq S
mq mq mq
qqqq qqqq qqqq
.
We find thus the complete integral
=++
∫∫∫
11 22 33
12312 1 2 3
12 3
() () ()
(,, ;, ,) d d d
() () ()
Sq Sq Sq
Sq q q a a h q q q
fq fq fq
,
which annuls each of the three ratios. The trajectory of the particle will be given by the
equations
++=
++=
∫∫∫
∫∫ ∫
123
1
11 22 33
123
11 22 33
2
11 22 33
12 3
ddd
,
() () ()
() () ()
dd d
,
() () ()
() () ()
qqq
b
Sq Sq Sq
fq fq fq
qq qq qq
b
Sq Sq Sq
fq fq fq
(19.2.82')
the motion on the trajectory being specified by the equation
()
++=+
∫∫∫
222
11 22 33
3
11 22 33
123
ddd
2
() () ()
() () ()
qq qq qq
tb
Sq Sq Sq
fq fq fq
.
(19.2.82'')
If
===
123
0UUU , then one obtains the equations of a straight line in elliptic
co-ordinates.
In case of an electrized particle in an electromagnetic field (see Sect. 19.1.3.3), the
formula (19.2.88) leads to the Hamilton–Jacobi equation
()()
+− −+=
,, 0
1
0
iiii
SSqASqAqA
m
.
(19.2.83)
19.2.3.2 Mechanical Systems with Two degrees of freedom
In the case of a mechanical system with two degrees of freedom (e.g., the motion of
a particle on a plane or on a surface – a holonomic constraint) the Hamilton–Jacobi
equations reads

MECHANICAL SYSTEMS, CLASSICAL MODELS
198
∂∂
⎛⎞
+=
⎜⎟
∂∂
⎝⎠
12
12
,, , ; 0
SS
SHqq t
qq
.
(19.2.84)
By means of a complete integral
=
1212
(, ;, ;)SSqqaat, the integrals of the canonical
equations will be given by
∂∂∂∂
=== =
∂∂∂∂
12 1 2
121 2
,,,
SSS S
bbpp
aaq q
.
(19.2.84')
If the constraint is scleronomic, then we ca take
=− +
121
(, ;,)ShtSqqah, the
reduced Hamilton–Jacobi equation being
∂∂
⎛⎞
=
⎜⎟
∂∂
⎝⎠
12
12
,, ,
SS
Hqq h
qq
.
(19.2.85)
The motion of the mechanical system is specified by
∂∂ ∂ ∂
==+ = =
∂∂ ∂∂
1212
112
,,,
SS S S
btb p p
ah qq
.
(19.2.85')
The trajectory of the representative point (for various values of the constant
1
b ) are
normal to the curves
= constS .
In case of a heavy particle
P , which is moving in a vertical plane, the reduced
Hamilton-Jacobi equation reads
⎡⎤
∂∂
⎛⎞⎛⎞
+−=
⎢⎥
⎜⎟⎜⎟
∂∂
⎝⎠⎝⎠
⎣⎦
22
2
12
2
mS S
gx h
xx
,
the
1
Ox -axis being horizontal, while the
2
Ox -axis is along the descendent vertical;
because
1
x is a cyclic co-ordinate, we search a solution of the form =+
12
()Sax xϕ ,
being led to the equation
′
+−=
⎡⎤
⎣⎦
22
122
()
2
m
axgxhϕ
,
wherefrom
=+ −+
∫
2
121 11 1 2 2
(,;,) 2 2 dSx x a h ax h a gx x.
The trajectory of the particle is given by the equation
−=−−+=
−+
∫
21
2
11 1 1 2 1
2
12
d
22
22
xa
xa x ha gx b
g
ha gx
,
(19.2.86)
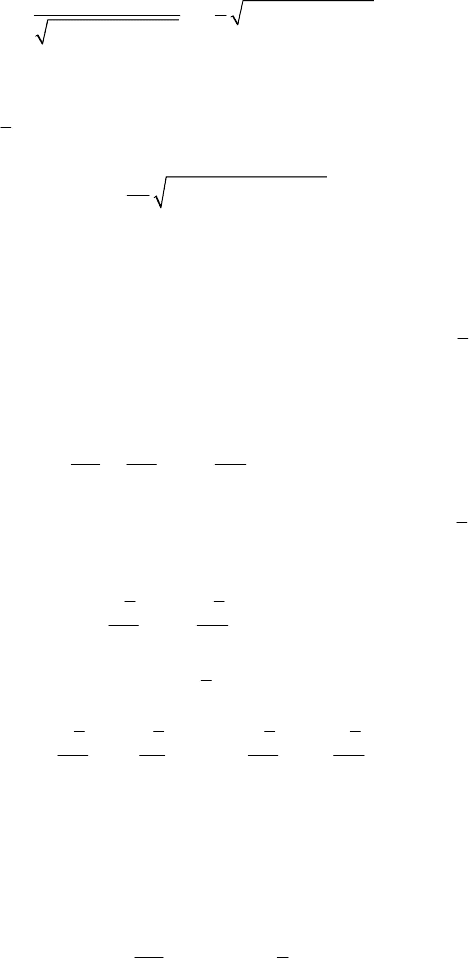
Hamiltonian Mechanics
199
being an are of parabola, tangent at the vertex to the straight line
=−
2
21
(2)/2xahg,
and the motion on this trajectory is specified by
=−+=+
−+
∫
2
2
12 2
2
12
d
1
22
22
x
ha gx tb
g
ha gx
.
(19.2.86')
From (19.2.86), (19.2.86') one obtains
=++
11 2 1
()xatb b, the motion of the
projection of the particle on the horizontal being uniform (see Sect. 7.1.2.1 too). The
curves
= constS are the semi-cubical parabolas
()
+−+=
3
2
11 1 2
1
22const
3
ax h a gx
g
,
(19.2.86'')
which can be obtained one from the other by a translation along the
1
Ox -axis; these
curves are normal to the straight line
=−
2
21
(2)/2xahg on which they have a
cuspidal point. Varying the constant
1
b , one obtains a family of parabolic trajectories
(by a translation along the
1
Ox -axis too), normal to the curves = constS , the general
theoretical result being thus verified.
In case of a plane motion of a particle, the Hamilton–Jacobi equation will of the form
⎡⎤
∂∂
⎛⎞⎛⎞
++−=
⎜⎟⎜⎟
⎢⎥
∂∂
⎝⎠⎝⎠
⎣⎦
22
12
12
1
(, ;) 0
2
SS
SUxxt
mx x
,
(19.2.87)
in Cartesian co-ordinates; if
= 0U
, then we take =− +
12
(, )ShtSxx, being led to
the reduced Hamilton–Jacobi equation
∂∂
⎛⎞⎛⎞
+=+
⎜⎟⎜⎟
∂∂
⎝⎠⎝⎠
22
12
2( )
SS
mU h
xx
.
(19.2.87')
A complete integral
=− +
121
(, ;,)ShtSqqah
leads to the sequences of relations
∂∂ ∂ ∂
==+ = =
∂∂ ∂∂
1212
112
,,,
SS S S
btb p p
ah x x
.
(19.2.87'')
The first equation specifies the trajectory of the particle in the plane
2
Λ and the second
equation corresponds to the motion on this trajectory; the last two equations complete
the solution of the problem in the space
4
Γ .
Let, e.g., be an elliptic oscillator, to which corresponds Hamilton’s function
()()
=+++
22 22
12 12
1
22
k
Hppxx
m
,
(19.2.88)

MECHANICAL SYSTEMS, CLASSICAL MODELS
200
where
k is an elastic constant. We notice that this function is of the form (19.2.44),
where
=+ =
22
/2 /2, 1,2
jj j
gpmkx j ; denoting ==,const
jjj
gaa it results
⎛⎞
=−=
⎜⎟
⎝⎠
2
2,1,2
2
j
jj
kx
pma j
.
(19.2.88')
We obtain the complete integral
()
=
⎛⎞
=− + + −
⎜⎟
⎝⎠
∑
∫
2
2
12
1
2d
2
j
jj
j
kx
Saat ma x
.
The Hamilton–Jacobi theorem allows to write the relations
=+ = = =
−
∫
22
d2
1
,, ,1,2
jj
jj
jj
xa
k
tb A j
mk
Ax
ω
ω
.
Effecting the quadrature, we get
()
=+=sin , 1,2
jj j
xA tbjω ,
(19.2.88'')
remaining to put the initial conditions.
We obtain the Hamilton–Jacobi equation
() ()
()
∂∂
⎡⎤
++−=
⎢⎥
∂∂
⎣⎦
22
11
,; 0
2
SS
SUrt
mr r
θ
θ
,
(19.2.89)
in polar co-ordinates (
==
12
,qrqθ
). If = 0U
, then we have =− + (,)ShtSrθ
and the reduced Hamilton–Jacobi equation is given by
()
∂∂
⎛⎞ ⎛⎞
==+
⎜⎟ ⎜⎟
∂∂
⎝⎠ ⎝⎠
22
2
1
2
SS
mU h
r
r
θ
.
(19.2.89')
Starting from the complete integral
=− +
1
(,; , )ShtSrahθ , the trajectory and the
motion on it will be given by
∂∂
==+
∂∂
12
1
,
SS
btb
ah
,
(19.2.89'')
and the generalized momenta by
∂∂
==
∂∂
,
r
SS
pp
r
θ
θ
.
(19.2.89''')
