Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

Hamiltonian Mechanics

171

for a finite variation, integrating along the trajectory of the representative point in the

space

E .

19.2.1.6 Hamilton’s Principal Function

Taking the final moment

t as an arbitrary moment t , we can define the function S

in the form

∫

12 12

( , ,..., , , ,..., ; )d

Sqqqqqqττ L .

(19.2.26)

As a matter of fact, this quantity can be called Lagrangian action (shortly, action),

corresponding – in a non-conservative case – to the quantity (19.2.17).

If we take into account the equations of motion at the moment

t , written in the form

00 000 0

12 1 2

00 000 0

12 1 2

( ; , ,..., , , ,..., ),

( ; , ,..., , , ,..., ), 1,2,..., ,

qqtqq qpp p

pptqq qpp pj s

then we get

00 000 0

12 1 2

( ; , ,..., , , ,..., )

SStqq qpp p. Hamilton proposed to eliminate the

generalized momenta at the initial moment; there results the function

12 1 2

( ; , ,..., , , ,..., )

SStqq qpp p,

(19.2.27)

called the Hamilton principal function.

We can calculate

∂

=+=

∂



But

∂∂∂∂

−=

∂∂∂∂

( , ,..., , , ,..., ; )

SSSS

qHqqq t

qqqq

 L ,

with the notation

, 1,2,...,

pSqj s=∂ ∂ =

. Hence, Hamilton’s principal function

must verify the equation in

. On the other hand,

∂

=+=−

∂

ddddd

jjj

SqStpqHt



(19.2.28)

If we take into account all the arguments in (19.2.27), then we can write

=−−

dddd

jjj

Spq Htpq.

(19.2.28')

Putting the condition that this is a total differential, we find again the Hamilton-Jacobi

equation, as well as the sequence

∂∂ = =, 1,2,...,

Sq p j s; the essential constants

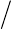
MECHANICAL SYSTEMS, CLASSICAL MODELS

172

being

00 0

, ,...,

qq q, we can write ∂∂ = =

, 1,2,...,

Sq p j s. The first subsystem of

relations determines the motion of the representative point in the space

; associating

the second subsystem of relations, we obtain the motion of the representative point in

the space

Γ .

Thus, Hamilton showed, in 1834, the possibility to obtain the final equation of

motion at the moment

t (the canonical co-ordinates as functions of time), by means of

a complete integral of the equation in

S . But the complete integral used by Hamilton is

not arbitrary; indeed, the essential constants which have been used are the initial values

of the canonical co-ordinates. Thus, one obtains a vicious circle: to obtain the final

equations of motion, Hamilton’s principal function is necessary, while to set up this

function, one must know the final equations of motion. The essential merit of Jacobi

consists in showing how one can avoid this vicious circle; indeed, Jacobi showed, in

1837, that the final equations of motion can be obtained by means of an arbitrary

complete integral of the Hamilton–Jacobi equation (19.2.9).

19.2.2 Systems of Equations with Separate Variables

The setting up of a complete integral of the Hamilton–Jacobi partial differential

equation can be realized, in many cases, in the form of a sum of

s functions of only

one generalized co-ordinate; in this case, we say that we have to do with a system of

equations with separate variables, which has interesting properties. We mention that the

separability is a property connected both to the system and to the chosen independent

co-ordinates. One puts thus the problem to determine the conditions of separability, as

well as the form of the system which verifies such conditions; we consider thus natural

systems with

s degrees of freedom, the motion of which is described by means of s

Lagrangian co-ordinates. There are a few cases (e. g., the problem of small oscillations)

in which the separation leads to

s independent equations, each one containing only one

generalized co-ordinate. In general, one cannot isolate a particular generalized

co-ordinate, studying its variation as in the case of a system with only one degree of

freedom; but, in a certain sense, we can consider the variation of a single co-ordinate,

neglecting the behaviour of the other co-ordinates.

One cannot give the general form of the systems of equations with separate (or with

separable) variables. Therefore, we will limit ourselves to the catastatic (hence

holonomic and scleronomic) systems for which the kinetic energy is a positive definite

quadratic form in the generalized velocities. In what follows, we will present firstly the

case of mechanical systems with two degrees of freedom. After some particular cases of

separability, we will study – further – the general case of mechanical systems with

s degrees of freedom, in the frame of Stäckel’s theory.

19.2.2.1 Mechanical Systems with Two Degrees of Freedom

We notice first of all that any scleronomic mechanical system with a single degree of

freedom is separable, the complete integral of the corresponding Hamilton–Jacobi

equation being of the form

Hamiltonian Mechanics

173

=− +(;; ) (; )Sqth ht Sqh.

(19.2.29)

Passing to the scleronomic mechanical systems with two degrees of freedom, we will

limit ourselves to the case of orthogonal systems, so that in the expression of the kinetic

energy does not intervene the product of two generalized velocities; hence,

()

11 1 22 2

Tgqgq

.

(19.2.30)

In this case, Hamilton’s function reads

()

=+−

11 2 22 2

HgpgpU

(19.2.31)

where

=>=>

11 22

1/ 0, 1/ 0gggg and U are functions of class

C in the

generalized co-ordinates

q and

q ; we have supposed that the generalized forces

derive from a simple potential. There results the Hamilton–Jacobi equation

⎡⎤

∂∂

⎛⎞ ⎛⎞

+−=

⎢⎥

⎜⎟ ⎜⎟

∂∂

⎝⎠ ⎝⎠

⎣⎦

11 22

gg Uh

(19.2.32)

where the complete integral is of the form

=− +

121

(, ;,)ShtSqqah; to realize a

separation of the form

12 1 111 2 21

(,,;,) (;,) (;,)Sq q a h S q a h S q a h

(19.2.33)

it is necessary to have

+=+

∂

⎛⎞

====

⎜⎟

∂

⎝⎠

11 22

12 2

(;,) , 1,2, .

kkk

ggUh

qaa k a h

ϕϕ

(19.2.34)

Differentiating with respect to

a and

a , respectively, we obtain

+= +=

11 22 11 22

1,1 2,1 1,2 2,2

0, 1gg ggϕϕ ϕϕ.

The coefficients

g and

g being positive, it results that the derivatives

1,1 2,1

,ϕϕ and

1,2 2,2

,ϕϕ, respectively, cannot be identically zero (for any generalized co-ordinates); as

well

∂

∂∂

∂

⎡⎤

−= = ≠

⎢⎥

∂∂∂∂∂

⎣⎦

1,1 2,2 1,2 2,1

12 1 2

(, )

det det 0

(, )

aa q q q a

ϕϕ

ϕϕ ϕϕ

MECHANICAL SYSTEMS, CLASSICAL MODELS

174

We can write

11 22

12 12

QQ QQ

the functions

===(), (), 1,2

kkkkkk

PPqQQqk , being given by

==−= =−

1,2 2,2

12 1 2

1,1 2,1 1,1 2,1

,,,PP Q Q

ϕϕ

ϕϕϕ ϕ

(19.2.34')

The potential

U must be given by

(19.2.35)

where the functions

(), 1,2

kkk

UUqk== are

−−

==−

11,2 22,2

1,1 2,1

ϕϕ ϕϕ

ϕϕ

(19.2.34'')

Resulting the kinetic energy

()

⎛⎞

=+ +

⎜⎟

⎝⎠

12 1 2

111

TQQ q q

,

(19.2.35')

it is necessary that Hamilton’s function be of the form

=−

11 22 1 2

12 12

Pp Pp U U

QQ QQ

(19.2.36)

The corresponding reduced Hamilton–Jacobi equation (19.2.15) is given by

()

⎡⎤

∂∂

⎛⎞ ⎛⎞

+−+=

⎢⎥

⎜⎟ ⎜⎟

+∂ ∂

⎝⎠ ⎝⎠

⎢⎥

⎣⎦

1212

12 1 2

11 1

PPUUh

QQ q q

Choosing the function

in the form (19.2.33), this equation is decomposed in two

equations of only one variable

∂∂

⎛⎞ ⎛⎞

=+− =++

⎜⎟ ⎜⎟

∂∂

⎝⎠ ⎝⎠

11112 221

PhQUaPhQUa

where

a is an arbitrary constant. Hence, the complete integral is given by

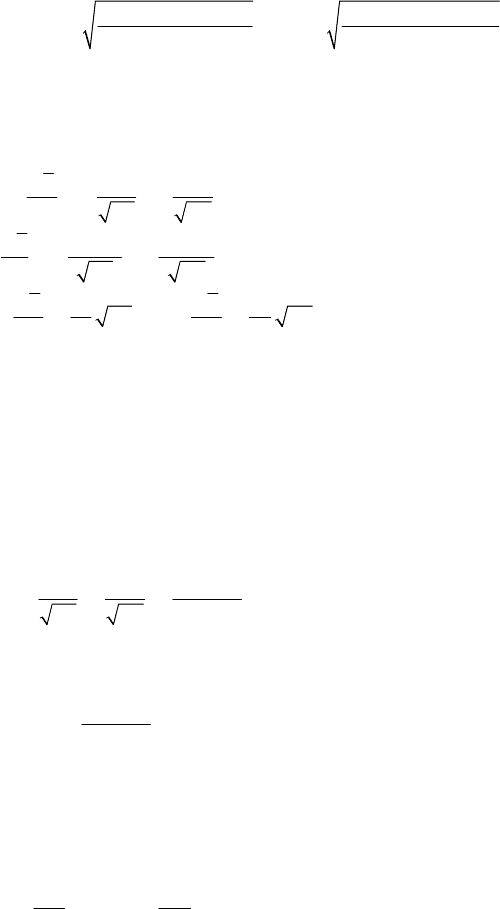
Hamiltonian Mechanics

175

()()

111 221

12 1 1 2

(, ;;,) d d,

hQ U a hQ U a

Sq q ta h ht q q

+− ++

=− + +

∫∫

(19.2.37)

the condition of separability imposed above being sufficient too.

Applying the Hamilton–Jacobi theorem, we obtain

∂

−= − =−

∂

=+=−

∫∫

11 22

Qd Qd

(19.2.38)

∂∂

== ==

∂∂

112 2

11 22

pRp R

qP qP

(19.2.38')

where

() ()

=+− =++

11 1 1 1 1 22 2 2 2 1

() 2 , () 2Rq P hQ U a Rq P hQ U a .

(19.2.38'')

The equations (19.2.38) specify the motion of the representative point in the

space

Λ , being sufficient to solve the Lagrangian problem; by differentiation, these

equations read

(19.2.39)

We denote

τ ,

(19.2.39')

where

τ can be considered as a conventional time in the motion of the representative

point on the corresponding trajectory in the space

Λ ; we notice that +>

0QQ , so

that

τ increases together with t . We obtain the equations

⎛⎞ ⎛⎞

⎜⎟ ⎜⎟

⎝⎠ ⎝⎠

ττ

(19.2.39'')

which can be considered each one as in the case of a mechanical system with only one

degree of freedom (see Sect. 7.1.1.1); but the relation between

t and τ depends on

both generalized co-ordinates. However, the motion can be studied independently, in a

certain measure. Obviously, the two motions would be independent if the sum

would be constant (certainly, we should, simultaneously, have

constQ and

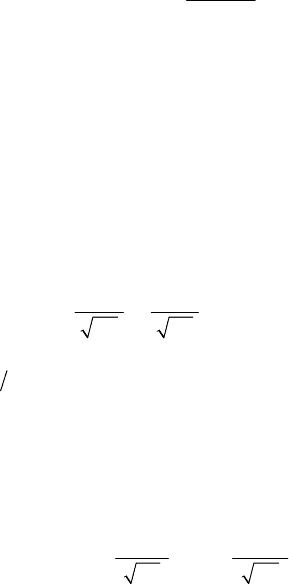
MECHANICAL SYSTEMS, CLASSICAL MODELS

176

constQ ); the motion would be only approximately independent if the sum

QQ would vary not very much.

Let us assume that the sum

is bounded for all the values of the generalized

co-ordinates (at least for all the values which are taken by these co-ordinates during the

considered motion), so that

<+<

0 QQ N, N finite for any t . In this case

→∞

τ together with →∞t and we can make an appreciation of the general nature

of the motion with respect to each generalized co-ordinate. If the generalized

co-ordinate

q , e.g., is – at the beginning – between two consecutive simple real zeros

≤≤

11 1 1 1

()( )Rq qαβ, then takes place an oscillatory motion in time, between

these values, for any moment

; the motion is periodical in τ , but is not periodical in

t , yet it will be called motion of libration. Th sign of the radical will be taken + or – as

q is increasing or decreasing, respectively. If →

q γ , where

γ is a double root of

R , for t (and τ ) tending to infinite, then one can speak about an asymptotic (limit)

motion. If the sum

QQ is not bounded, e.g. if +→∞

QQ together with t

(which can take place if

q and

q tend to infinite with

), then it can happen that the

integral

∞

∫

be convergent; in this case

lim ττ for →∞t . If, in this case, we have

≤≤

11 1

qαβ at the initial moment, then we have no more a motion of libration and

=≤≤

111 1

lim ,ql lαβ, for →∞t . As well, if →

q γ ,

γ double root, then the

motion is pseudoasymptotic. Obviously, one can make analogous considerations for the

generalized co-ordinate

q .

In the case in which librations can take place for each of the two generalized

co-ordinates, the motion of the mechanical system is periodical if

=∈

∫∫

νν_

(19.2.40)

Thus, if

nnν , where ∈

,nn ` , have no one common factor, then, after

librations corresponding to the generalized co-ordinate

q and after

n librations

corresponding to the generalized co-ordinate

q , the mechanical system returns to the

previous situation (the representative point

∈

P Λ returns to the same position), as

well as in what concerns the position and the velocities. Obviously, the period will be

∫∫

11 22

Qd Qdqq

Tn n

(19.2.40')

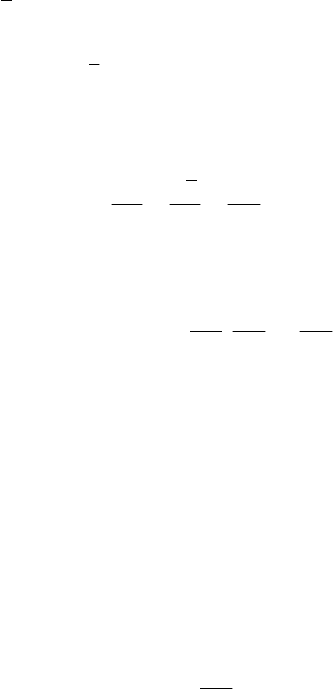
Hamiltonian Mechanics

177

ν is an irrational number, then the motion is not periodical, while the trajectory of

the representative point

∈

P Λ is contained in a rectangular interval ( ≤≤

kk k

qαβ,

= 1, 2k ), being an open curve; in this case the motion is quasi-periodical.

We mention that we can choose the generalized co-ordinates corresponding to the

mechanical system with two degrees of freedom in various modes; e.g., in case of the

motion of a particle subjected to the action of a central force of Newtonian attraction

one can use, in the plane of the motion, polar or parabolic or confocal co-ordinates etc.

Correspondingly, one can obtain a separation of the variables in several modes for the

same problem.

19.2.2.2 Mechanical Systems with

s Degrees of Freedom. Particular Cases of

Hamiltonians

In case of a generalized conservative mechanical system with

s degrees of freedom

we search a complete integral (19.2.15'), trying to obtain a decomposition of the

function

−12 12 1

( , ,..., ; , ,..., , )

Sq q q a a a h in the form

()

−

∑ 12 1

; , ,..., ,

SSqaaah.

(19.2.41)

In this case

∂

∂∂

=== =

∂∂∂

, 1,2,...,

jjj

pjs

qqq

(19.2.41')

The reduced Hamilton–Jacobi equation becomes

∂∂

∂

⎛⎞

⎜⎟

∂∂ ∂

⎝⎠

, ,..., , , ,...,

Hqq q h

qq q

(19.2.41'')

Observing that

()

−

12 1

; , ,..., , , 1,2,...,

jjj

pfqaa ahj s,

(19.2.42)

we get

()

−

=− +

∑

∫

12 1

; , ,..., , d

Sht fqaaahq

(19.2.43)

and the condition (19.2.6) reads

∂

⎡⎤

≠

⎢⎥

∂

⎣⎦

det 0

(19.2.43')

MECHANICAL SYSTEMS, CLASSICAL MODELS

178

The generalized co-ordinates will be given by the system of algebraic equations

∂

== −

∂

∑

∫

∑

∫

d , 1,2,..., 1,

qbk s

qtb

(19.2.42')

so that the generalized momenta will result in the form (19.2.42). The above integrals

can be considered between the limits

c and

q , where

c are fixed constants,

independent on the integration constants

a and

b .

The most simple case in frame of the above considerations is that in which the

variables are separated in the structure of Hamilton’s function, so that

()

∂

==≠=

∂

, ,..., , ( , ), 0, 1,2,...,

jjjj

HHgg g g gqp j s

(19.2.44)

Imposing the conditions

==( , ) , 1,2,...,

jjj j

gqp a j s, we can apply the theorem of

implicit functions; it results

==( ; ), 1,2,...,

jjjj

pfqaj s.

(19.2.45)

The reduced Hamilton–Jacobi equation leads to

( , ,..., )

hHaa a, so that the

complete integral will be of the form

()

=− +

∑12

, ,..., ( ; )d

jj j

SHaaat fqaq.

We notice that

∂∂

wherefrom

()

−

∂∂ =∂ ∂ ≠

jj jj

fa gp ; but ∂∂ = ≠0,

fa jk, so that

∂∂

⎡⎤

=≠

⎢⎥

∂∂

⎣⎦

∏

det 0

the condition (19.2.43') being fulfilled. Hence, the sequences of algebraic relations

which give the canonical co-ordinates will be (19.2.45) and

Hamiltonian Mechanics

179

−

∂∂

∂

⎛⎞

==+=

⎜⎟

∂∂ ∂

⎝⎠

∫∫

(;)

d d , 1,2,...,

jjjj

jjj

jj j

pfqa

qqbtjs

ap a

(19.2.45')

the problem being thus reduced to quadratures.

If we choose Hamilton’s function in the form

()

−

∂

== ≠= =

∂

, ; , , 0, 1,2,..., ; 0

jj jj

Hgg gg qp j sg

(19.2.46)

then we can impose the conditions

−

== ==

( ; , ) , 1,2,..., , 0,

jjjj

ga qp a j sa a h ;

the theorem of implicit functions allows to write

−

====

( , , ), 1,2,..., , 0,

jjj j

pfqaaj sa ah.

(19.2.47)

The reduced Hamilton–Jacobi equation is identically verified because we have taken

gah

; the complete integral will be of the form

−

=− +

∑

∫

(; ,)d

jjj

Sht fgaaq.

Taking into account considerations analogue to those in the preceding case, it results

()

−

∂∂ =∂ ∂ ≠

jj jj

fa gp ; we notice that ∂∂ = <0,

fa jk, too. As above, the

condition (19.2.43') is verified, the value of the determinant being reduced to the

product of its elements (all non-zero) of the principal diagonal. We notice that

+++

∂∂∂

111

jjj

gfg

paa

The trajectory of the representative point

∈

P Λ will be specified by the equations

−

+++ +

−

∂

∂∂

⎛⎞

⎜⎟

∂∂ ∂

⎝⎠

∂∂

⎛⎞

−==−

⎜⎟

∂∂

⎝⎠

∫∫ ∫

∫

111 1

(; ,)

(;,)

dd d

d , 1,2,..., 1 ,

jjj j

jj j

pfqa a

pfgaa

qq q

aa p

qbj s

(19.2.47')

and the motion on this trajectory by the equation

−

∂

⎛⎞

⎜⎟

∂

⎝⎠

∫

(; ,)

sss

pfqa h

qtb

(19.2.47'')

MECHANICAL SYSTEMS, CLASSICAL MODELS

180

The generalized momenta are given by the relations (19.2.47), the problem being thus

completely solved.

Another interesting case is that in which the Hamiltonian is of the form

()

+++

∂∂

=−≠=

∂∂

...

,,,

...

, , 0, 1,2,..., .

jjjj

gg g

Hggqp

gg g

ggqp h j s

(19.2.48)

The reduced Hamilton–Jacobi equation (19.2.15) reads

∂∂

⎡⎛ ⎞ ⎛ ⎞⎤

−=

⎜⎟⎜⎟

⎢⎥

∂∂

⎣⎝ ⎠ ⎝ ⎠⎦

∑

,,0

jj jj

gq hgq

We can denote

()()

−== =

∑

, , , 1,2,..., , 0

jjj jjj j j

gqp hgqp aj s a ,

wherefrom, applying the theorem of implicit functions, we get

()

==; , , 1,2,...,

jjjj

pfqahj s.

(19.2.49)

The complete integral of the Hamilton–Jacobi equation will be

()

=− +

∑

∫

;, d

jjj j

Sht fqahq.

We notice that (we take into account the relation

−

=− + + +

12 1

( ... )

aaa a, the s th

essential constant being

h )

∂∂ ∂ ∂

∂

∂∂

⎛⎞

−=−=−=≠

⎜⎟

∂∂ ∂ ∂∂ ∂ ∂

⎝⎠

∂∂ ∂

⎛⎞

−−===−

⎜⎟

∂∂ ∂

⎝⎠

1, 1, 0, ,

0, 1,2,..., , , 1,2,..., 1 ;

kk k k

kk k k l

jj j

gg f f

hh kl

pp a pp a a

gg f

hgjskls

pp h

it results

−

∂∂∂

⎛⎞

⎡⎤

=− −

⎜⎟

⎢⎥

∂∂∂

⎣⎦

⎝⎠

∏

det

jjj

fgg

app

Δ ,

where