Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

Hamiltonian Mechanics

201

(,) () ()

Ur U r U

θθ,

(19.2.90)

then Hamilton’s function is of the form (19.2.46), with

==−=

== =− + ==

(, ) () ,

(;, ) () .

rr r r

ggp U a

Hg ggrp Ur a h

θθ θ θ

θθ

One obtains the generalized momenta

[]

⎡

⎤

=++

⎢

⎥

⎣

⎦

2(),

2() .

pmUa

pmUr h

θθ

(19.2.90')

Taking into account the partial derivatives

()

(

)

∂+

∂

−+

∂

== =

∂∂

gp Ua

pm m

pm m a

θθ θ

the formulae (19.2.47') give the trajectory of the particle

P in the form

−=

−+

∫∫

dd2

()

rUr h

(19.2.90'')

and the formula (19.2.47'') specifies the motion on this trajectory by the equation

()

−+

∫

()

Ur h

(19.2.90''')

The problem is thus reduced to quadratures.

=>/, 0Ukrk (case of forces of Newtonian attraction), then the

Hamilton-Jacobi equation is written in the form

()

∂∂

⎡⎤

++ −=

⎢⎥

∂∂

⎣⎦

SSk

mr r rθ



(19.2.91)

MECHANICAL SYSTEMS, CLASSICAL MODELS

202

As a matter of fact, this case is contained in the previously considered one. The

generalized momenta are (

== >0, / , 0

UUkrk

, and θ is a cyclic co-ordinate)

()

=+−

pma

pmh

(19.2.91')

The trajectory of the particle is given by

=−

+−

∫

d2r

rhr kr a

(19.2.91'')

the motion on the trajectory being specified by

()

+−

∫

d2rr

hr kr a

(19.2.91''')

Let us suppose that the particle

P lies on a surface S for which the element of arc

is given by a relation of the form

()

⎛⎞

=+ + = = =

⎜⎟

⎝⎠

d,(),(),1,2

jjjjjj

sQQ PPqQQqj

(19.2.92)

In this case, one obtains the kinetic energy

()

⎛⎞

=+ +=

⎜⎟

⎝⎠

22 2 2

12 1122

12 12

qq PpPp

TQQ

PP QQ



(19.2.92')

If the particle is subjected to no one given force (

= 0U ), then it results =HT and

we can apply Liouville’s theorem. By separation of variables, hence by quadratures,

one can obtain thus the possible trajectories (depending on the integration constants); in

fact, thus are specified the geodesic lines of the surface. The surfaces which have this

property are called Liouville’s surfaces.

19.2.3.3 Problem of Two Particles. Motion of Planets

The problem of two particles has been considered in Sects. 19.3.2.3 and 18.1.3.2,

assuming the action of forces of Hamiltonian attraction. The generalized system has

three degrees of freedom and we can choose the generalized co-ordinates

===

123

,,qrq qθϕ; assuming that we study the relative motion of a particle with

respect to the other one, we take the latter one as origin of the frame of reference. We

can thus use the results obtained in Sect. 19.2.3.1 for the motion of a free particle (in

spherical co-ordinates – the formulae (19.2.75'), (19.2.75''), and (19.2.75''')).

Hamiltonian Mechanics

203

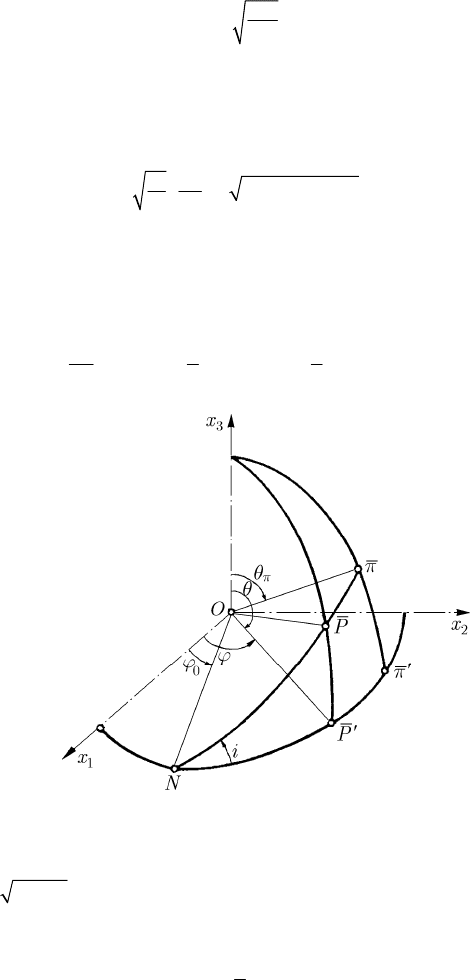
We assume that the initial position of the particle in on the line of nodes

ON , in the

plane

Ox x (Fig. 19.1); hence, for =

tt we have == =

/2,θθ π ϕϕ. Imposing

these conditions, it results

=− =

btb

ϕ .

(19.2.93)

As far as we know, the trajectory of the particle is an ellipse of semi-major axis

a and

eccentricity

e ; in this case, =−

min

(1 )rae and =+

max

(1 )rae. By differentiation of

the equation (19.2.75'''), we obtain

=+−

rhrkra

The extreme values of the vector radius

r must annul the quantity under the radical.

From Viète’s relations, it results

+==−

max

min

2/rr akh, =−

max

min

(1 )rr a e

=−

/ah , wherefrom

()

−

=< = −=>

0, 1 0

22 2

kk k

haaep

(19.2.93')

Fig. 19.1 Motion of the Sun and of a planet

We notice that for a given colatitude

θ one must have −≥

/sin 0aa θ , hence

≥

arcsin /aaθ ; but

min

θ is just the complement of the angle i made by the plane

of the orbit with the plane

Ox x . Hence,

cos cos

aa i p i.

(19.2.93'')

MECHANICAL SYSTEMS, CLASSICAL MODELS

204

The trajectory will be given by (for

θ we take the inferior limit /2π , corresponding to

a point on the line of nodes, while for

r we take the inferior limit =−

min

(1 )rae,

corresponding to the pericentre

π )

[][]

−

=−

−

−=

+− − −

∫

(1 )

cos d

sin sin cos

sin d

sin sin cos

(1 ) (1 )

ae ae

ϕϕ

ϑϑ

ρρρ

(19.2.94)

while the motion on the trajectory will be specified by

[][]

()

−

=−

+− − −

∫

(1 )

(1 ) (1 )

att

ae ae

ρρ

(19.2.94')

At the moment in which the particle attains the pericentre

π , the second equation

(19.2.94) becomes

==−

−−

∫∫

22 22

/2 /2

sin d sin d

sin cos sin cosii

ππ

θθ

ππ

ϑϑ ϑϑ

ϑϑ

with

=−

/pkmb

. By integrating, we get

cos

arcsin

sini

(19.2.93''')

wherefrom

=cos sin sini

(19.2.93

)

Considering the relations between the elements of the spherical triangle

′

Nππ

on a

sphere with the centre

O and of unit radius (the point π is the piercing point of the

radius with this sphere), we see that

= N

. These results correspond to those

obtained in Sect. 9.2.2.4 in the study of the orbit of a satellite. As a matter of fact, we

can imagine that at the pole

O is situated the Sun, the particle P being a planet; in this

case, the plane

Ox x is the plane of the ecliptic, while the point π is the perihelion.

Thus, all six parameters (

,,, ,aei tϕ and

) which define the orbit of the planet are

determined.

We notice that

Hamiltonian Mechanics

205

[][]

(

)

−−

−

+− − −

−+ −

−+

−−

===−−

−

=− −

∫∫

(1 ) (1 )

(1 )

(1 ) (1 )

arcsin arcsin arcsin

4( )

arcsin ,

ae ae

ap ap

ae ae

aap

ap a

rp rp

er er

aa p

ρρ

ρρρ

ρρ ρ

as well as

==−

−

∫

sin d

cos

arcsin

sin

sin cos

ϑϑ

where the arc

= NPχ corresponds to an arbitrary position on the orbit (the point P is

the intersection of the radius

OP with the sphere of unit radius); hence,

(

)

−

−=−−arcsin

so that

()

(

)

−−

−= − =cos cos arcsin

pr pr

er er

Finally, we find the known equation of the trajectory in its plane

()

+−1cos

(19.2.95)

corresponding to the equation (9.2.6). Starting from the equation (19.2.94') and using

the constant

h given by (19.2.93'), we find again the integral given in Sect. 9.2.1.3,

which leads to Kepler’s equation (9.2.13). The first equation (19.2.94) specifies the

motion in the plane of the ecliptic.

Knowing that the trajectory is a plane curve, the problem can be treated in another

way too, choosing the plane of the trajectory as plane

Ox x . Considering, further, the

relative motion of a planet with respect to the Sun, we can use polar co-ordinates as in

Sect. 19.2.3.2 (the mechanical system formed by the two particles has two degrees of

freedom in the plane of the motion); the Hamilton-Jacobi equation (19.2.91) leads thus

to the classical equation of the trajectory.

But we can make also a study in orthogonal Cartesian co-ordinates, after Jacobi. The

reduced Hamilton–Jacobi equation will be

()

∂∂

⎛⎞⎛⎞

+=+

⎜⎟⎜⎟

∂∂

⎝⎠⎝⎠

SS k

xx r

(19.2.96)

MECHANICAL SYSTEMS, CLASSICAL MODELS

206

Taking an arbitrary point

P on the

Ox -axis, so that =

OP r , and denoting

PP ρ , we have

()

=+ = −+

22 2

12 1 2

,rxx xr xρ .

(19.2.97)

We will show that the function

′

∫

(19.2.96')

where

′

=− =+,rrσρσρ

(19.2.97')

is a complete integral of the equation (19.2.96),

r being an essential constant. Indeed,

observing that

σ and

′

depend on

x and

x by means of r and ρ , it results

−−

∂

⎛⎞ ⎛ ⎞

⎛⎞ ⎛⎞

=+ +−− +

⎜⎟ ⎜⎟

⎜⎟ ⎜ ⎟

′

∂+ +

⎝⎠ ⎝⎠

⎝⎠ ⎝ ⎠

∂

⎛⎞ ⎛ ⎞

⎛⎞ ⎛⎞

=+ +−− +

⎜⎟ ⎜⎟

⎜⎟ ⎜ ⎟

′

∂+ +

⎝⎠ ⎝⎠

⎝⎠ ⎝ ⎠

11 11

22 22

xxr xxr

Skh kh

xr r r r

xx xx

Skh kh

xr r r r

ρσ ρσ

wherefrom, using the notation (19.2.97), we find (the terms which contain the product

of the two radicals disappear)

−+

∂∂

⎡⎤

⎛⎞⎛⎞

⎛⎞

+=+ +

⎜⎟

⎜⎟⎜⎟

⎢⎥

∂∂ +

⎝⎠

⎝⎠⎝⎠

⎣⎦

−+

⎡⎤

⎛⎞

+− +

⎜⎟

⎢⎥

′

⎝⎠

⎣⎦

11 2

2( )2

xx r x

SS kh

xx r r

xx r x

ρσ

Taking into account the identities

−+

++− −

+==

′

−+

−−+ −

−= =

222 22

11 2

222 22

11 2

2( )2

xx r x

rr r r

rrr

xx r x

rr r r

rrr

ρρ σ

ρρρ

ρρ σ

ρρρ

one sees that the equation (19.2.96) is verified.

The equation of the trajectory and the motion on it will be given by

∂∂= = ∂∂=−

/,const,/Sr KK Shtt. We notice that

′

−−

∂∂

==− =−=−

∂∂ ∂ ∂

00 0 0

xr xr

rr r r

ρρ

σσ

ρρ

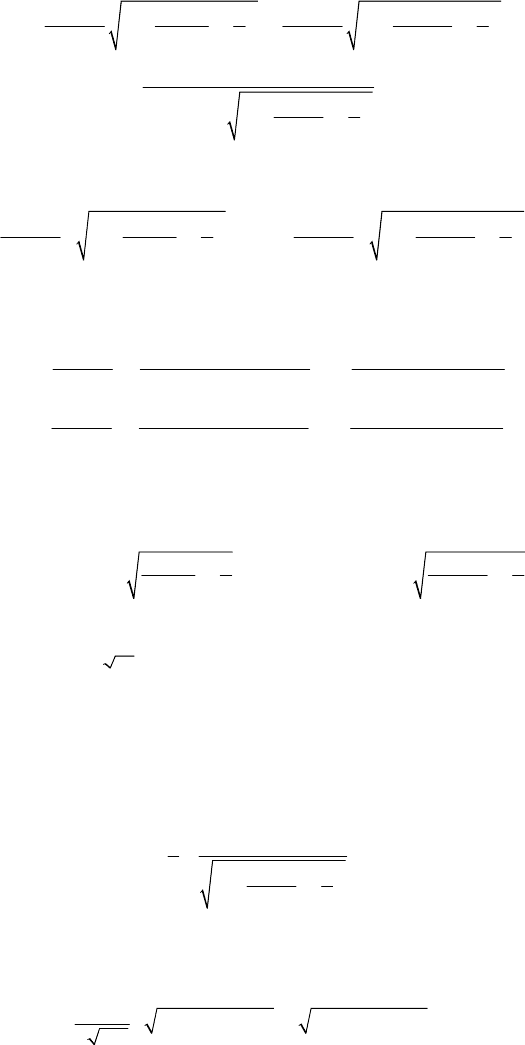
Hamiltonian Mechanics

207

so that the first equation leads to

()

′

−−

⎛⎞ ⎛ ⎞

−+− +

⎜⎟ ⎜ ⎟

′

⎝⎠ ⎝ ⎠

−=

⎛⎞

⎜⎟

⎝⎠

∫

xr xr

kh k h

mk s

sr m

ρσ ρσ

Effecting the quadrature, we can also write

−−

⎛⎞ ⎛ ⎞⎛⎞ ⎛⎞

−+−+ +=

⎜⎟ ⎜⎟

⎜⎟ ⎜ ⎟

′

⎝⎠ ⎝⎠

⎝⎠ ⎝ ⎠

xr xr

kh kh

mmK

ρσ ρσ

Because

−=−−

222

00 0

2( )rx r r r ρ , it results

()

′

−

−++ + −

−= =−

′

−

+−− − +

+= =−

222

100 00

222

100 00

rrr r r

ρρσσ

ρρ ρ

ρρσσ

ρρ ρ

obtaining thus the equation of the trajectory in bipolar co-ordinates (of poles

O and

P ) in the form

()

00 00

kh k h

rr rr K

σσ σσ

σσ

′′′

+− ++−+ +=

′

(19.2.98)

where

′

2/KrKmρ is a new integration constant. We have

= 0ρ

, =

rr for

the point

, hence

′

rσσ ; taking into account the form of the constant

′

, we

see that the trajectory, which is a conic, passes through the point

. The genus of the

conic depends on the sign of the constant

; in case of the Solar system we have

< 0h

, the conic being an ellipse.

The motion on the orbit will be specified by

′

−=

⎛⎞

⎜⎟

⎝⎠

∫

(19.2.98')

beginning from the point

P for which =

tt. If the orbit is parabolic ( = 0h ), then

the integration is immediate, obtaining Euler’s formula

()()

⎡⎤

−= ++ − −+

⎣⎦

000

tt r r r r

ρρ.

(19.2.98'')

MECHANICAL SYSTEMS, CLASSICAL MODELS

208

In the case in which

≠ 0h (elliptic or hyperbolic orbits), analogous formulae have

been given by Gauss.

19.2.3.4 Problem of the Two Centres

We take again the problem of two centres, considered in Sect. 18.3.2.4. The kinetic

energy is given by (18.3.55) and the simple potential reads (18.3.55'), obtaining

Hamilton’s function

()

()()

[]

⎛⎞

=− +

⎜⎟

−−

⎝⎠

−+−−

−

22 2 2

12 12

kk kk

λμ

(19.2.99)

where

λ and μ are elliptic co-ordinates in the plane; m is the mass of the particle,

and

characterize the centres of attraction (in inverse proportion to the squares of the

distances), the distance between these centres being

. We find the generalized

momenta

() ()

−−

22 22

22 2 2

,pm pm

λμλ λμμ

λμ

(19.2.100)

so that Hamilton’s function becomes

()()()

()()

[]

=− −+−

⎡

⎤

⎣

⎦

−+−−

−

22 222 222

12 12

Hm cpc p

kk kk

λμ λ μ

λμ

(19.2.99')

This Hamiltonian is of the form (19.2.51), hence of Liouville’s type, and one can make

the separation of the variables. Thus, we obtain – obviously – the same relations

(18.3.56), (18.3.56'), the trajectory and the motion on the trajectory being obtained by

quadratures (elliptic integrals). The relations (19.2.100) complete then the solution in

the phase space.

This problem has been considered for the first time by Euler (in the plane case); it

has been taken again in a three-dimensional treatment by Lagrange and then by Jacobi,

who integrated it by his general method of calculation. This research has been an

important impetus to enlarge the theory of elliptic integrals. We mention also the results

obtained by Serret, Desboves and Andrade in this direction.

G. Dincă studied, in 1965, the general motion of a particle subjected to the action of

n central forces (which pass through n fixed centres), in a resistant medium; the

problem is reduced to the above considerations, in some interesting particular cases.

These results can be seen also as a first step in the study of the problem of three

particles, which can be solved – in general – only by approximate methods of

calculation; besides, the results can be used in the general problem of

n particles too.

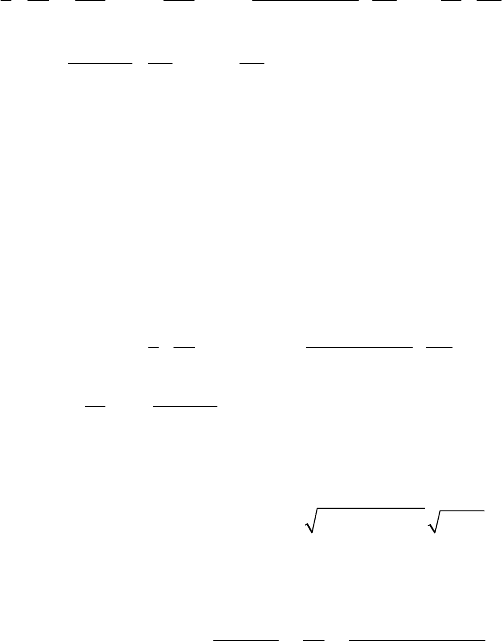
Hamiltonian Mechanics

209

19.2.3.5 Motion of the Rigid Solid

The Hamilton–Jacobi method can be applied, as well, in the case of the free or the

constrained rigid solid

S . As in Sect. 19.1.3.5, we will consider a heavy,

homogeneous rigid solid of rotation, of mass

M , which slides frictionless on a fixed

horizontal plane, having five degrees of freedom. Starting from Hamilton’s function

(19.1.96), one obtains the canonical equations (19.1.96'). The generalized co-ordinates

are

′′

,ρρ (which specify the position of the mass centre) and Euler’s angles ,ψθ and

ϕ ; the generalized momenta

,, ,ppp p

ψθ

and p

are corresponding to them,

I and

J are the moments of inertia with respect to the axis of rotation and to an axis normal

to this one (with respect to the movable frame of reference

R ), respectively, while the

function

()f θ specifies the applicate of the mass centre with respect to the fixed plane.

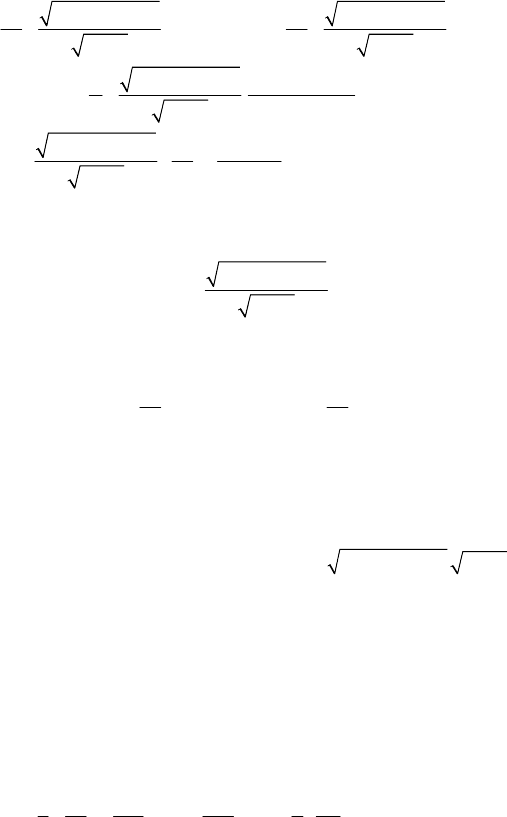
The Hamilton–Jacobi equation reads

()

⎧⎡ ⎤

∂∂ ∂ ∂

⎛⎞⎛⎞

⎛⎞

+++ +

⎨

⎜⎟

⎜⎟⎜⎟

⎢⎥

′′

∂∂ ∂ ∂

′

⎝⎠

⎝⎠⎝⎠

⎩⎣ ⎦

⎫

∂∂

⎛⎞

+−+=

⎬

⎜⎟

∂∂

⎝⎠

⎭

12 3

11 1 1

()

cos ( ) 0 .

sin

SS S S

Mf J

Mgf

ρρ θ ϕ

θθ

ψϕ



(19.2.101)

Because the constraints are scleronomic and the generalized co-ordinates

′′

,,ρρψ and

ϕ are cyclic, we can choose a complete integral of the form

′′

=− + + + + +

11 22 3 4

()Shta a a a Fρρψϕθ,

where

123

,,,ha a a and

a are integration constants. Replacing in the equation

(19.2.101), we get the equation

()

∂

⎡

−+ + +

⎢

∂

′

⎣

⎤

++ − + =

⎥

⎦

434

11 1

()

cos ( ) 0 ,

sin

haa

Mf J

aaaMgf

θθ

which determines the function

()F θ ; we obtain thus the complete integral

′′ ′

=− + + + + + +

∫

11 22 3 4

() ()dShta a a a Mf Jρρψϕ θ Θθθ,

(19.2.102)

where we have denoted

[]

()

+−

=− − −−

222

124 34

cos

() 2 ()

sin

aaa aa

hMhf

Θθ θ

(19.2.102')

the five constants being essential constants.

MECHANICAL SYSTEMS, CLASSICAL MODELS

210

Differentiating the function

S with respect to the initial constants, we find the

equations of the trajectory of the representative point

∈

P Λ in the form

()

′′

−=−=

′

−

−=

′

⎡⎤

−−−=

⎢⎥

⎣⎦

∫∫

∫

1122

34 4

() ()

d, d,

() ()

()

cos

sin

()

cos

cos d ,

sin

()

Mf J Mf J

Mf J

aa b

θθ

ρθρθ

Θθ Θθ

ψθ

Θθ

ϕθθ

Θθ

(19.2.103)

the motion along this trajectory being specified by the equation

′

−=

∫

()

Mf J

Θθ

(19.2.103')

Replacing the integral (19.2.103') in the first two equations (19.2.103), we obtain

() ()

′′

−= − −= −

btt btt

ρρ

;

(19.2.103'')

we find thus again a known result, in accordance to which the projection of the mass

centre on the fixed plane has a rectilinear and uniform motion. The components of the

generalized momentum will be

′

== = == +

1122 3 4

, , , , () ()papap ap ap Mf J

ψθ

θΘθ.

(19.2.103''')

Let be also the problem of the plane motion of a rigid straight bar, of mass

M ,

attracted by elastic forces (of elastic constant

k ) by the

Ox -axis, considered in Sects.

18.3.2.7 and in 19.1.3.5. Hamilton’s function is given by (19.1.97), where

′

ρ and

′

(the co-ordinates of the mass centre) and the angle of rotation

θ are the generalized

co-ordinates, while

I is the central moment of inertia with respect to an axis normal to

the plane of motion (see Fig. 18.12 too). The Hamilton-Jacobi equation will be

()

11 1

sin 0.

SS S

SkMI

ρθ

ρρ θ

⎧

⎡⎤

∂∂ ∂

⎫

⎛⎞⎛⎞

′

+++++=

⎨⎬

⎜⎟⎜⎟

⎢⎥

′′

∂∂ ∂

⎝⎠⎝⎠

⎭

⎩

⎣⎦



(19.2.104)

The constraints are scleronomic and

′

ρ is a cyclic co-ordinate, so that the complete

integral is of the form

′′

=− + + +

11 1 2 2

() ()Shta S Sρρ θ.