Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

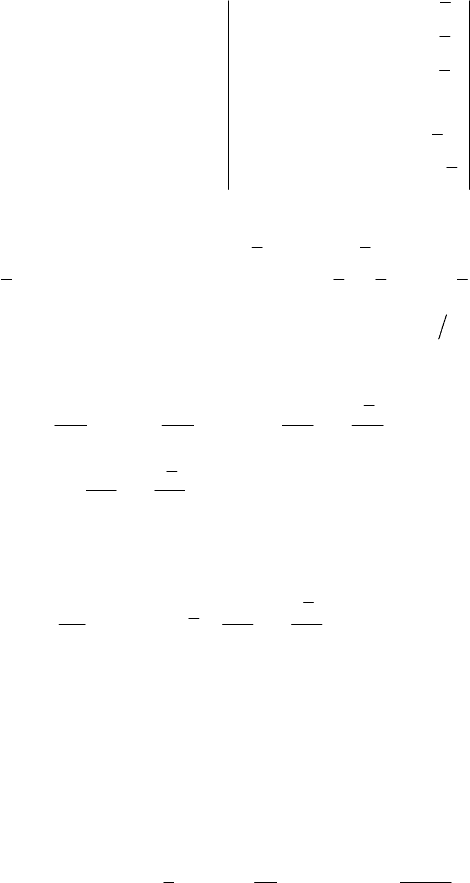
Hamiltonian Mechanics

181

−

1 0 0 ... 0 0

0 1 0 ... 0 0

001...00

... ... ... ... ... ... ...

000...01

111...11

Δ .

Expanding after the first column (the second minor after the first line) we obtain

−−

=⋅ +− − = −

1111

1(1)(1)

ggΔΔ Δ ; analogously, we get

−−

12ss

ΔΔ

−

g a.s.o. Finally, we can write =− + + + ≠

( ... ) 0

gg gΔ , the denominator of

the Hamiltonian cannot vanish, so that

⎡⎤

∂∂ ≠

⎣⎦

det 0

fa . The generalized

co-ordinates will be given by the relations

−

∂∂∂

∂

⎛⎞

+=−

⎜⎟

∂∂ ∂∂

⎝⎠

∂∂

⎛⎞

−− == −

⎜⎟

∂∂

⎝⎠

∫∫∫

∫

(;,)

dd d

d , 1,2,..., 1,

kkkk

ssss

kkk

kk kk

pfqah

fgg

qq h q

aa pp

hqbks

(19.2.49')

the motion on the trajectory of the representative point

∈

P Λ being specified by

−

∂∂∂

⎛⎞

=− =+

⎜⎟

∂∂∂

⎝⎠

∑∑

∫∫

(;,)

jjjj

jjj

jj j

pfqah

fgg

qg h qtb

hpp

(19.2.49'')

where

−

=− + + +

12 1

( ... )

aaa a; the relations (19.2.47) allow then the calculation

of the generalized momenta.

As a particular case, we can state

Theorem 19.2.2 (Liouville). If the kinetic energy and the potential energy of the

mechanical system are of the form

==−=−

∑

∑∑

∑

TQ VU

(19.2.50)

respectively, where

= ()

QOq, = ()

kkk

PPq, ==( ), , 1,2,...,

kkk

UUqjk s are

functions of only one variable, then the equations of motion can be obtained by

quadratures.

Indeed, in this case Hamilton’s function is of the form

MECHANICAL SYSTEMS, CLASSICAL MODELS

182

===

== =

⎡

⎤

−

⎢

⎥

⎣

⎦

=−=

∑∑∑

∑∑ ∑

111

11 1

() ()

()

sss

kk k k k k k k

kkk

ss s

jj jj

jj j

Pp U P q p U q

QQ Qq

(19.2.51)

hence a particular case of the function (19.2.48). We obtain thus the reduced Hamilton–

Jacobi equation

⎡⎤

∂

⎛⎞

−= =

⎢⎥

⎜⎟

∂

⎝⎠

⎣⎦

∑∑

() (),

kkk

PUqhQqha

where we took into account (19.2.15'). If

=+++

11 22

() ()... ()

SSq Sq Sq, then, by

separation of variables, we can decompose this system in the form

∂

⎛⎞

=+−= +++=

⎜⎟

∂

⎝⎠

( ) , 1,2,..., , ... 0

kkkkk

PhQqUaksaaa

We get, in this case, the complete integral (ensured by the above proof)

()

−

+−

=− +

+++++

∑

∫

12 1

2 ...

kkk

hQ U a

Sht q

hQ U a a a

The trajectory of the representative point

P in the configuration space

Λ will be

given by the equation

∂

−= − =− = −

∂

∫∫

, 1,2,..., 1

bk s

(19.2.52)

while the motion on the trajectory will be specifies by

∂

==−

∂

∑

∫

(19.2.52')

where we have denoted

−

=+−=−

=+++++

12 1

( ) 2 ( ), 1,2,..., 1,

( ) 2 ( ... ).

kk k k k k

ss s s s

Rq PhQ U a k s

Rq PhQ U a a a

(19.2.52'')

There result then the generalized momenta

Hamiltonian Mechanics

183

∂

== =

∂

, 1,2,...,

pjs

(19.2.52''')

As in the case

= 2s , the differential equations of motion may be written in a compact

form

11 22

... d ,

( ) ( ) ... ( )

() () ()

Qq Qq Qq

Rq Rq Rq

τ==== =

+++

(19.2.52

)

where

τ is a conventional measure of the time. In connection to these results one can

make a discussion analogue to that in the case

= 2s .

The mechanical systems characterized by the kinetic energy and the potential energy

(19.2.50) are called Liouville’s systems. In the case

= 2s , as we have seen in the

preceding subsection, the mechanical systems, which lead to systems of equations with

separate variables, are just of such a form; but if

> 2s , then not any mechanical

system, separable from the point of view of the canonical co-ordinates, is characterized

by the formulae (19.2.50).

19.2.2.3 Stäckel’s Theorem

As in the case = 2s , we consider the orthogonal, scleronomic mechanical systems,

studied by P. Stäckel in 1893–1895; in this case (Stäckel, P., 1908),

== = ≥

∑∑

, ( , ,..., ) 0,

, ( , ,..., ) ,

jj j j jj jj

Tgq gpggqqq

gUUqqq



(19.2.53)

where

, 1,2,...,

gj s= , and U are functions of class

. We can state

Theorem 19.2.3 (Stäckel). The Hamilton–Jacobi equation built up by means of the

kinetic energy and of the potential energy

=−VU (19.2.53) is with separate variables

if and only if there exists a non-singular square matrix

, ( )

jk jk jk

qλλλ≡=

⎡⎤

⎣⎦

λ ,

and a column matrix

[]

, ( ), , 1,2,...

jjjj

qjk sμμμ≡= =μ , so that to have

=δ =

∑

, 1,2,...,

jk ks

gksλ ,

(19.2.54)

∑

gUμ .

(19.2.54')

Indeed, if the reduced Hamilton–Jacobi equation

∂

⎛⎞

−= =

⎜⎟

∂

⎝⎠

∑

gUhha

(19.2.55)

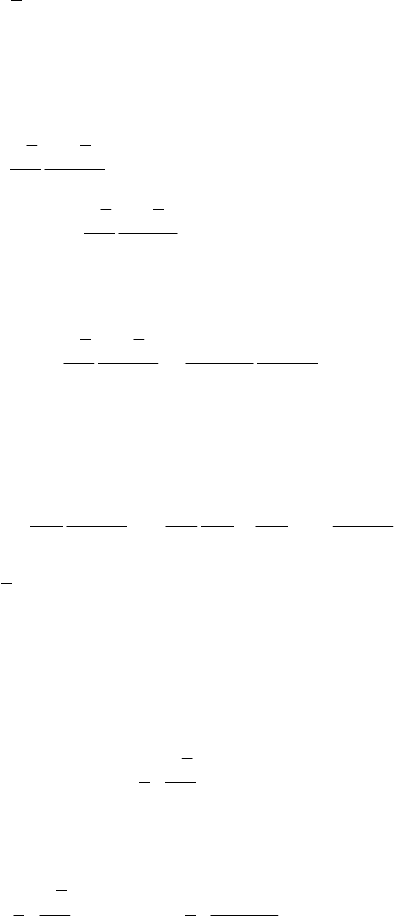
MECHANICAL SYSTEMS, CLASSICAL MODELS

184

is separable, then we can write a complete integral for which

∑ 12

( ; , ,..., )

SSqaaa.

(19.2.55')

Introducing in (19.2.55), this equation must be identically satisfied with respect to the

essential constants

a ; differentiating with respect to these constants, we can write

∂∂

== −

∂∂∂

∑

0, 1,2,..., 1

gks

qaq

(19.2.56)

∂∂

∂∂∂

∑

qaq

(19.2.56')

Denoting

∂∂

∂∂∂ ∂ ∂∂

()

jj j

Sq S

qaq q aq

we notice that the relations (19.2.56), (19.2.56') correspond to the relations (19.2.54);

on the other hand,

==( ), , 1,2,...,

jk jk

qjk sλλ , and

∂∂ ∂

⎡⎤ ⎡⎤

∂∂

∂

== ≠

⎡⎤

⎢⎥ ⎢⎥

⎣⎦

∂∂∂ ∂∂ ∂ ∂∂

⎣⎦ ⎣⎦

det det ... det 0

jj j

SS S

qaq qq q aq

λ ,

because the function

leads to a complete integral. Observing that

∑

g λ ,

the equation (19.2.55) allows to write

⎡

⎤

∂

⎛⎞

=−

⎢

⎥

⎜⎟

∂

⎝⎠

⎢

⎥

⎣

⎦

∑

Ug a

λ .

Denoting

∂

⎛⎞ ⎡ ⎤

=−= −

⎜⎟

⎢⎥

∂∂

⎝⎠ ⎣ ⎦

()

js js

μλ λ,

we see that the relation (19.2.57) corresponds to the relation (19.2.54'), while

( ), 1,2,...,

jjj

qj sμμ==. Hence, the conditions (19.2.54), (9.2.54') are necessary

conditions of separability.

Hamiltonian Mechanics

185

Taking into account the relations of conditions (19.2.54), (19.2.54'), we can write the

Hamilton–Jacobi reduced equation in the form

====

∂

⎛⎞

−=

⎜⎟

∂

⎝⎠

∑∑∑∑

1111

ssss

jj jj

kjk

jjkj

gPag

μλ

or in the form

⎡⎤

∂

⎛⎞

−−=

⎢⎥

⎜⎟

∂

⎝⎠

⎢⎥

⎣⎦

∑∑

kjk

λμ ,

where

−12 1

, ,...,

aa a are arbitrary constants. To calculate a complete integral we use

the sum (19.2.55'), where the functions of only one variable are given by the equations

∂

⎛⎞

== +=

⎜⎟

∂

⎝⎠

∑

( ) 2 , 1,2,...,

jj j

kjk

qajs

ϕλμ.

(19.2.58)

It results

∫

() ()d, 1,2,...,

jj j j

Sq q q j sϕ .

(19.2.58')

We obtain easily

∂

⎡⎤

∂

⎡⎤

== ≠

⎡⎤

⎢⎥

⎣⎦

⎢⎥

∂∂ ∂∂

⎣⎦

∏

det det det 0

jjj

aq aq

so that the integral obtained on this way for the equation in

S is a complete one.

Hence, the conditions (19.2.54), (19.2.54') are sufficient conditions of separability too,

Stäckel’s theorem being completely proved.

The solution of Lagrange’s problem (the trajectory of the representative point

P in

the space of configurations

Λ and the motion on this trajectory) is given by the

Hamilton-Jacobi theorem in the form

∂

== == −

∂∂

∂

==+

∂

∑∑

∫

∑

∫

,1,2,...,1,

()

jk k

bk s

(19.2.59)

The solution of Hamilton’s problem in the phase space

Γ is then specified by the

generalized momenta

==( ), 1,2,...,

jjj

pqj sϕ .

(19.2.59')

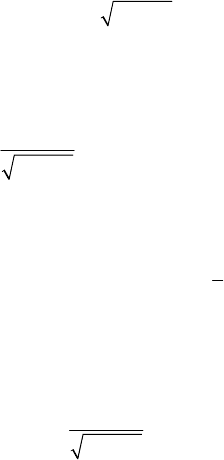
MECHANICAL SYSTEMS, CLASSICAL MODELS

186

Thus, the considered problem is solved by quadratures.

The obtained solution depends on the integration constants

a and ,

1,2,...,js= ; as one can notice, the constant

plays a special rôle, being the energy

constant

h . The formula (19.2.59') shows that the generalized momentum

p depends

only on the generalized co-ordinate

; in exchange, the generalized velocities

==( ), 1,2,...,

jjj

qg qj sϕ ,

(19.2.60)

depend on all the generalized co-ordinates.

The relation (19.2.60) allows to write

== =

d d , 1,2,...,

()

gt j s

(19.2.60')

too, where

=, 1,2,...,

sτ , is a local measure of time, different for each co-ordinate;

the sign of the radical is positive or negative as

q increases or decreases, respectively,

during time, because

≥ 0

g . If ≥>0

jjj

gg and if ()

qϕ is a continuous

function, then the general character of the motion, corresponding to the co-ordinate

q ,

is specified by (19.2.60')

It is interesting to see that, by differentiating the relation (19.2.59), we obtain

=δ =

∑

,1,2,...,

()

jk ks



(19.2.61)

Comparing with the relation (19.2.54), we find again the equations (19.2.60').

The conventional time

τ tends to infinite together with t , the nature of the

variation of the generalized co-ordinate

q depending on the zeros of

()

qϕ

. Thus, if

q is between two consecutive simple zeros ()

qϕ (with >() 0

qϕ for

qαβ), then we have a motion of libration in

q , while if →

q γ for

→∞t , where

is a double zero for ()

qϕ , then we have an asymptotic (limit)

motion. We must notice that if a motion of libration takes place indefinitely between

and

β , then this one is not, in general, periodical with respect to time. As a matter of

fact, as in the case

= 2s , the discussion of the motion with respect to the generalized

co-ordinates is of a particular interest.

→ 0

P for →∞t , then it is possible that

τ does tend to a finite limit (not to

an infinite one); in this case, the motion with respect to

q is pseudoasymptotic. If

≤≤

qαβ at the initial moment, then we do not obtain a motion of libration, while

(eventually after a finite number of oscillations)

=lim

ql, ≤≤

lαβ for

→∞t .

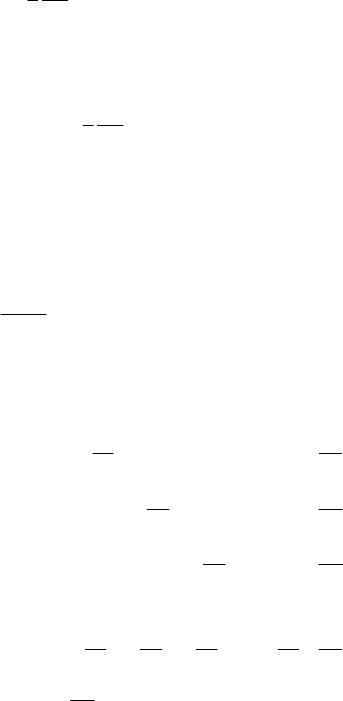
Hamiltonian Mechanics

187

We mention that Stäckel’s theorem leads. at the same time, to

s first integrals of

Lagrange’s equations; thus, the relations (19.2.60) lead to

−= =

∑

, 1,2,...,

kjk

aj s

βλ



(19.2.62)

so that

⎛⎞

−= =

⎜⎟

⎝⎠

∑

,1,2,...,

aj s

λβ



(19.2.62')

where

λ is the normalized algebraic complement corresponding to the element

λ in

the matrix

λ , with =δ

kkl

λλ .

One see easily that for

== = =

∑

, ( ), ( ), , 1,2,...,

jjj

lll

gPPqQQqjls

(19.2.63)

and

⎡⎤

−

⎢⎥

−

⎢⎥

⎡⎤

⎣⎦

⎢⎥

−

⎢⎥

⎣⎦

0 0 ... 0

00...0

00 ...0

... ... ... ... ... ...

111 1

...

sss ss

PPP PP

(19.2.63')

== =, ( ), 1,2,...,

jjjj

UUqj s

(19.2.63'')

we find again Liouville’s system; taking into account the expansion of

Δ , from the

previous subsection, one can show that

−−

=− ≠

⎡⎤

⎣⎦

∑

∏

det ( 1) 0

jk l

PQλ

(19.2.63''')

The conditions in Stäckel’s theorem can be satisfied if we take

−−

== ==

11 22 1, 1

23 34

... , ... ,..., , 1

ss ss

sss

gg ggψψ ψ ψψ ψ ψ ,

(19.2.64)

MECHANICAL SYSTEMS, CLASSICAL MODELS

188

with

= ()

lll

qψψ ,

= 1,2,...,ls

; in this case

−

⎡⎤

⎢⎥

−

⎢⎥

−

⎢⎥

⎡⎤

⎣⎦

⎢⎥

−

⎢⎥

⎣⎦

10 0...00

10...00

01...00

... ... ... ... ... ...

000...10

000... 1

(19.2.64')

with

−

=− ≠

⎡⎤

⎣⎦

det ( 1) 0

λ . The system is separable if the potential

is of the

form

−

=+++

123 234 1

... ...

ssss

U μψψ ψ μψψ ψ μ ψ μ .

(19.2.64'')

Formally, taking into account the relations (19.2.54), (19.2.54'), we can express the

kinetic energy and the simple potential in the form

∑

∑∑

∑

kk k

Tggq



(19.2.65)

which has an affinity with Liouville’s formulation.

But we must notice that Stäckel’s theorem does not cover the conditions of

separability for an arbitrary Hamilton–Jacobi equation; such conditions could not yet be

found.

Let

λ be the algebraic complement of the element

λ in the determinant

Δ=

⎡⎤

⎣⎦

det

; in this case, by an expansion after the last column, we can write

Δ=

λλ , so that =∂Δ∂

λλ. The normalized algebraic complement being

, , 1,2,...,

kjk

jk sλλ=Δ = , it results =δ

kks

λλ , so that we can take

, 1,2,...,

jjs

gjsλ== in Stäckel’s theorem.

19.2.2.4 Levi-Civita’s Conditions

Another attempt to the problem of the separation of variables in the Hamilton-Jacobi

equation has been made by T. Levi-Civita in 1904. To do this, we will calculate the

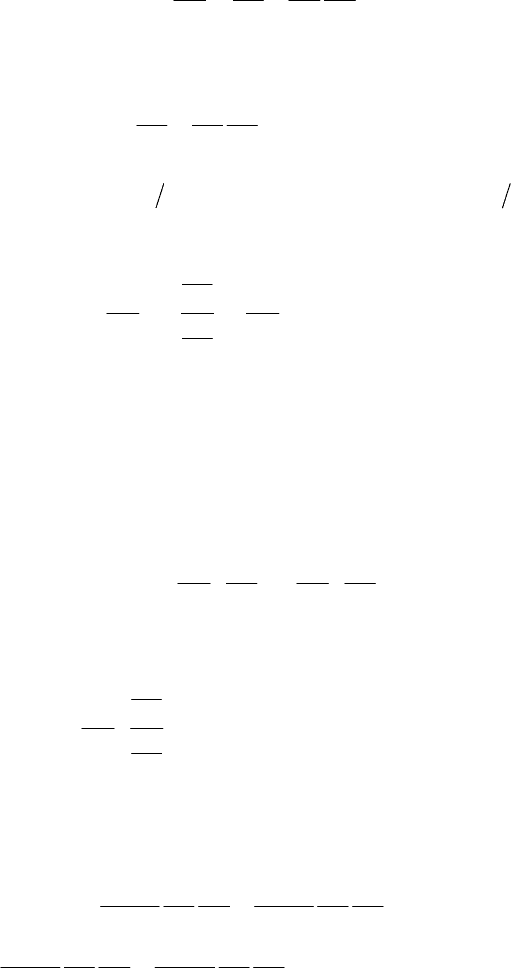
Hamiltonian Mechanics

189

total derivative of the Hamilton–Jacobi equation (19.2.41'') with respect to

q in the

form

∂

∂∂

=+ =

∂∂∂

jj j

HHH

qqpq

But the generalized momenta are given by (19.2.41'), so that

= ()

kkk

ppq, obtaining

∂

∂∂

+==

∂∂∂

0(!), 1,2,...,

jjj

qpq

We must assume that

∂∂≠0

Hp ; otherwise, we should have ∂∂=0

Hq too, but

we suppose that no one co-ordinate is cyclic. It results

∂

=− = ≠

∂

(!), 0,

(19.2.66)

We obtain thus the necessary and sufficient conditions which must be fulfilled by

Hamilton’s function, so that the function (19.2.41) does correspond to a complete

integral of the equation (19.2.41''). Other developments in this directions have been

made by V. G. Imshenetskiĭ in 1869, by Burgatti in 1911, by M. S. Yarov-Yarovoi in

1963 and by others.

Imposing also the conditions of integrability

∂∂

⎛⎞

⎜⎟

∂∂

⎝⎠

qq qq

we are led to Levi-Civita’s conditions

∂

⎛⎞

⎜⎟

∂

=≠ =

⎜⎟

∂

⎜⎟

∂

⎝⎠

0, , , 1,2,...,

jkjk s

(19.2.67)

Taking into account (19.2.66), we find

−(1)/2ss relations (we notice that the

relations are symmetric with respect to the indices

j and k ) of the form

∂∂∂ ∂∂∂

−

∂∂∂∂ ∂∂∂∂

∂∂∂ ∂∂∂

−+ =≠=

∂∂ ∂ ∂ ∂∂ ∂ ∂

0, , 1,2,..., .

jj j j

kkkk

jj j j

kkkk

HHH HHH

qqpp qqpq

HHH HHH

jkj s

qp q p pp q q

(19.2.67')

MECHANICAL SYSTEMS, CLASSICAL MODELS

190

We mention that these conditions, which must be fulfilled by Hamilton’s function so

that the Hamilton-Jacobi equation be with separate variables, have a general character;

but, unlike the conditions which appear in the less general case considered by Stäckel,

these conditions can hardly be manipulate. As a matter of fact, they could be used only

in the cases of two or three degrees of freedom; we mention that the case of two degrees

of freedom has been considered by G. Morera in 1887. In 1944, Forbat completes

Levi-Civita’s conditions with

s condition of the form

∂∂ ∂∂

−==

∂∂∂ ∂∂∂

0, 1,2,...,

jjj

HH HH

pqt ppt

;

(19.2.67'')

the results can be thus applied to the case of rheonomous mechanical systems too.

19.2.2.5 A New Formulation of Hamilton–Jacobi Type

One sees easily that, in the canonical system of equations (19.1.14), the generalized

co-ordinates

and the generalized momenta

play a symmetric rôle, being

sufficient to replace Hamilton’s function

H by −H . In this order of ideas, the

Hamilton–Jacobi partial differential equation (19.2.9) can be replaced by the partial

differential equation

∂∂ ∂

⎛⎞

−=

⎜⎟

∂∂ ∂

⎝⎠

, ,..., , , ,..., ; 0

WW W

WH pp pt

pp p



(19.2.68)

12 12

( , ,..., , , ,..., ; )

Wp p p a a a t is a complete integral of this equation, the condition

∂

⎡⎤

≠

⎢⎥

∂∂

⎣⎦

det 0

(19.2.68')

taking place, then the canonical co-ordinates

===( ), ( ), 1,2,...,

jj j j

qqtpptj s,

will be given by the sequences of relations

∂∂

=− = =

∂∂

, , 1,2,...,

bqj s

(19.2.68'')

where

a are essential constants, while

b are constants conjugate to these ones.

Making a transformation of Legendre type and taking into account Donkin’s theorem

(the formula (19.1.8)), we can write

SW pq;

(19.2.69)

thus, the new variable

p and the new function W will be given by

∂∂

==−

∂∂

pWqS

(19.2.69')