Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

Hamiltonian Mechanics

161

∂∂ =, 1,2,...,

Sqk s; eliminating these constants between the mentioned relations, we

obtain one or more relations of the form

∂∂ ∂

⎛⎞

⎜⎟

∂∂ ∂

⎝⎠

, ,..., ; ; , , , ,..., 0

SS S

fqq qtSS

qq q



(19.2.2)

If there results only one relation, this one is a partial differential equation of first order,

non-linear in general, with respect to the function

; this function, of the form (19.2.1),

represents the complete integral of the partial differential equation (19.2.2).

Let be, e.g., a partial differential equation of the form

∂∂ ∂

⎛⎞

⎜⎟

∂∂ ∂

⎝⎠

, ,..., 0

SS S

qq q

(19.2.3)

The corresponding complete integral will be

−− +

=+++ ++

11 22 1 1 1

...

ss s

Saq aq aq Cq a,

(19.2.3')

with

()

−

12 1

, ,..., , 0

faa a C .

(19.2.3'')

In case of Clairaut's equation

∂∂ ∂ ∂∂∂

⎛⎞

++++ −=

⎜⎟

∂∂ ∂ ∂∂∂

⎝⎠

12 12

... , ,..., 0

SS S SSS

qq q f S

qq q qqq

(19.2.4)

we get the complete integral

()

=++++

11 22 1 2

... , ,...,

ss s

Saq aq aq faa a.

(19.2.4')

In case of the equation (19.2.3) (which does not contain the function

S ), the arbitrary

constant

+1s

a appears in an additive form in the complete integral (19.2.3'), while, in

case of the equation (19.2.4) (which contains the function

S ), no one additive constant

intervenes in the complete integral (19.2.4').

Let be thus a partial differential equation

∂∂ ∂

⎛⎞

⎜⎟

∂∂ ∂

⎝⎠

, ,..., ; ; , ,..., 0

SS S

fqq qt

qq q

(19.2.5)

which does not contain the function

S ; the complete integral is thus of the form

()

12 12 1

, ,..., ; ; , ,...,

SSqq qtaa a a,

(19.2.5')

one of the arbitrary constants being additive. We notice that in the relations (19.2.1'),

(19.2.1'') intervene now only

s arbitrary constants, called essential constants, which

MECHANICAL SYSTEMS, CLASSICAL MODELS

162

can be determined univocally from the relations (19.2.1''), assuming that the Hessian

with respect to the generalized co-ordinates and to the arbitrary constants is non-zero

(

S is a function of class

C )

∂

⎡⎤

≠

⎢⎥

∂∂

⎣⎦

det 0

(19.2.6)

As a matter of fact, the integral (19.2.5') is complete if this necessary and sufficient

condition is fulfilled. Replacing in (19.2.1'), we see that the corresponding partial

differential equation can be written in the form

∂∂ ∂

⎛⎞

⎜⎟

∂∂ ∂

⎝⎠

, ,..., ; ; , ,..., 0

SS S

Sqqqt

qq q



;

(19.2.7)

the complete integral which contains

s essential constants and verifies the condition

(19.2.6) is given by

()

12 12

, ,..., ; ; , ,...,

SSqq qtaa a.

(19.2.7')

If we denote

qt and if we take into account the notations (19.2.1'), (19.2.1''),

then we can write the partial differential equation (19.2.5) in the form

()

12 1 2

, , ,..., ; , , ,..., 0

fqqq q p pp p ;

(19.2.8)

the ordinary differential equations of the characteristics of the partial differential

equation (19.2.8) read

() ()

∂∂

==−= ==

∂∂

ddp

, , , , 0,1,2,...,

kk k k

qq pp k s

ττ

(19.2.8')

We can say that the partial differential equation of first order (19.2.8) is associated to

the system of ordinary differential equations of first order (19.2.8') and inversely.

Let us take Hamilton’s function

12 1 2

( , ,..., , , ,..., ; )

HHqq qpp pt as function ϕ

in the equation (19.2.7); we obtain thus the partial differential equation

∂∂ ∂

⎛⎞

⎜⎟

∂∂ ∂

⎝⎠

, ,..., , , ,..., ; 0

SS S

SHqq q t

qq q



(19.2.9)

where the generalized momenta

p are replaced by the partial derivative

∂∂

Sq, = 1,2,...,js; the complete integral of this equation, called the Hamilton–

Jacobi equation (or the equation in

S ), is of the form (19.2.7'), with the condition

(19.2.6).

If we make

= tτ in the system of ordinary differential equations (19.2.8') and use

the notations which have been introduced, we get

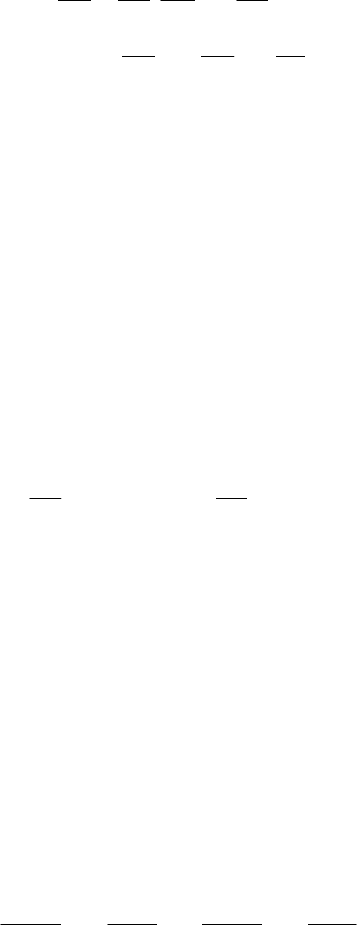
Hamiltonian Mechanics

163

∂∂

==−=

∂∂

∂

==−

∂

ddp

, , 1,2,..., ,

1, .

tpt q

ttt

(19.2.9')

The equations in the first row are just Hamilton’s canonical equations; the first equation

in the second row is an identity and the second one leads to the relation

d/dHtH=



which takes place along the trajectory of the representative point in the space

Γ .

Hence, the Hamilton–Jacobi equation is associated to Hamilton’s equations, the study

of this equation being thus equivalent to the study of the canonical equations; but

sometimes, the integration of the Hamilton–Jacobi equation can be realized on a simpler

way or can give interesting suggestions for the integration of the canonical equations,

being useful to solve the mechanical problem thus put.

19.2.1.2 The Hamilton-Jacobi theorem

In connection with the Hamilton–Jacobi equation we can state

Theorem 19.2.1 (Hamilton–Jacobi). If

∈

is the complete integral (19.2.7')

(which verifies the condition (19.2.6)) of the Hamilton–Jacobi equation (19.2.9), then

the sequences

∂∂

== ==

∂∂

, const, , 1,2,...,

jj j

bb p j s

(19.2.10)

determine the solutions

= ()

qqt

and

= ()

ppt

, = 1,2,...,js, of the system of

canonical equations (19.1.14).

Starting from the first sequence of relations (19.2.10) (which is, in fact, a sequence of

first integrals), taking into account the condition (19.2.6), we can determine the generalized

co-ordinates

()

12 12

; , ,..., , , ,..., , 1,2,...,

qqtaa abb bj s==, by means of the

theorem of implicit functions; replacing then in the second sequence of the relation

(19.2.10), we obtain the generalized momenta

()

12 12

; , ,..., , , ,...,

pptaa abb b. The

integration constants

and

b of same index

=, 1,2,...,

, are called conjugate

constants.

Because the relations (19.2.10) must take place along the trajectory of the

representative point

in the space

at any moment

, their total derivatives with

respect to time must vanish; we will have

∂∂∂∂

+= +−=

∂∂ ∂∂ ∂∂ ∂∂

2222

0, 0

jj jj

SSSS

qqp

qa ta qq tq



(19.2.11)

We notice that, by introducing the complete integral (19.2.7') in the equation (19.2.9),

the latter one must be identically verified in generalized co-ordinates and essential

constants; differentiating this equation, successively, with respect to

a and to

q , we

obtain

MECHANICAL SYSTEMS, CLASSICAL MODELS

164

∂∂∂ ∂∂∂

+=+=

∂∂ ∂ ∂∂ ∂∂ ∂ ∂∂

2222

0, 0

jjjj

kk kk

SHS SHS

at p aq qt p qq

Subtracting these relations one of the other and observing that

∈

SC, we can write

∂∂

⎛⎞

−=

⎜⎟

∂∂ ∂

⎝⎠

∂∂ ∂

⎛⎞

−−−==

⎜⎟

∂∂ ∂ ∂

⎝⎠

0, 1,2,..., .

qa p

SH H

qp js

qq p q





(19.2.11')

Hence, these relations are equivalent to the relations (19.2.11). If the canonical

equations take place, then – obviously – the relations (19.2.11') are also verified. Let us

suppose now that the first sequence of the relations (19.2.11') holds; these relations can

be considered as a homogeneous system of linear algebraic equations with a non-zero

determinant (the Hessian (19.2.6)), which admits only trivial solutions, obtaining thus

the first subsystem of the canonical equations. If we take into account this result, the

second sequence of relations leads to the second subsystem of the canonical equations.

The theorem enounced above is thus proved.

Thus, the solution of the system of canonical equations (19.1.14) is reduced to the

finding of a complete integral of the Hamilton–Jacobi equations (19.2.9). The two

problems are equivalent, the Hamilton–Jacobi theorem being useful if we succeed to

obtain such a complete integral. The respective method of calculation is known as the

Hamilton-Jacobi method. We mention that the Hamilton–Jacobi theorem can be put in

connection with the Theorem 19.1.19 of Liouville (see Sect. 19.1.2.4).

We notice that a complete integral of the Hamilton–Jacobi equation is not the

general integral of this equation; indeed a complete integral contains, in general, a

smaller number of solutions than the general integral. But starting from a complete

integral, we can find again the partial differential equation to which it corresponds, on

the way shown in Sect. 19.2.1.1 for the function (19.2.5') with

a .

We mention that the equation

()

12 12

, ,..., ; ; , ,..., 0

SSqq qtaa a

(19.2.12)

represents the equation of a movable or deformable hypersurface in the configuration

space

Λ ; this equation is, in fact, a wave surface and pays an important rôle in the

undulatory mechanics. The trajectory of the representative point in this space is

orthogonal, at each point, to the mentioned surface.

19.2.1.3 Properties of the Integration Constants

As it is known (see Theorem 19.1.4), Lagrange’s brackets formed by to integration

constants of the system of canonical equations are constants along the trajectory of the

representative point in the space

Γ (see Sect. 19.1.2.1). We try now to specify the

integration constants which are introduced by the Hamilton-Jacobi method.

Let thus be

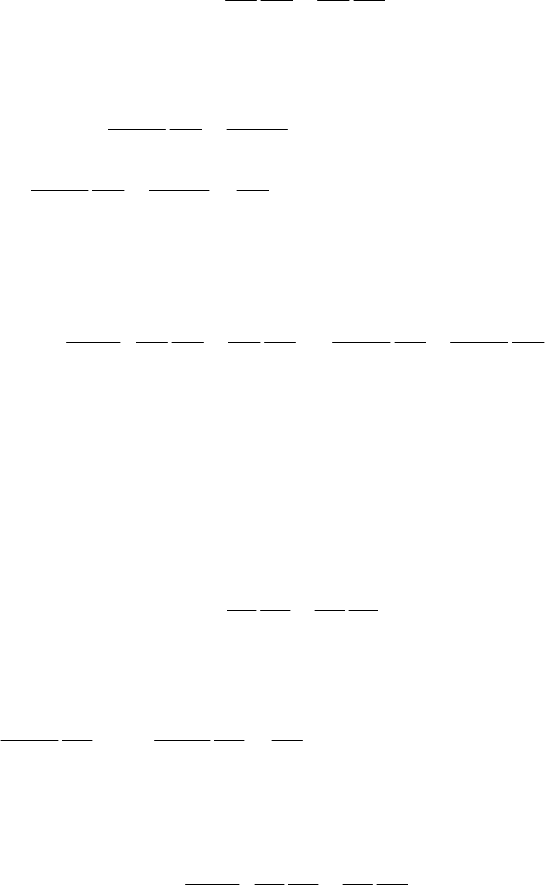
Hamiltonian Mechanics

165

[]

∂∂ ∂∂

=−

∂∂ ∂∂

ii ii

qp qp

aa aa

Differentiating the sequence (19.2.10) with respect to

a , we obtain

∂

∂∂

∂∂ ∂ ∂ ∂

∂

∂∂

+= =

∂∂ ∂ ∂ ∂ ∂

, , 1,2,..., .

ij j

lkk k

qa a aa

jk s

qa a a q a

(19.2.13)

Inverting

j by

we obtain other analogous relations. Replacing the partial derivative

of the generalized momenta in Lagrange’s bracket considered above it results

[]

∂∂ ∂

∂∂∂

⎛⎞

=−+−

⎜⎟

∂∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂

⎝⎠

222

il il i l

ij j ij ji

lkkk k

qq q

SSS

qq a a a a a q a aq a

The first sum contains products of symmetric and antisymmetric factors with respect to

the indices

i and l , being thus equal to zero; taking into account the first relations

(19.2.13) and observing that

∈

SC, one sees that the other sums vanish too, so that

[

]

==, 0, , 1,2,...,

aa jk s.

(19.2.14)

Analogically,

[]

∂∂ ∂∂

=−

∂∂ ∂∂

ii ii

qp qp

bb bb

Differentiating the sequences (19.2.10) with respect to

b , we get

∂

∂∂

=δ = =

∂∂ ∂ ∂∂ ∂ ∂

, , , 1,2,...,

ij j

klkk

jk s

qa b qq b b

(19.2.13')

Inverting

j by k , we obtain other relations, analogue to the above ones. Replacing the

partial derivatives of the generalized momenta in this Lagrange bracket, we get

[]

∂∂

∂

⎛⎞

=−

⎜⎟

∂∂ ∂ ∂ ∂ ∂

⎝⎠

il il

ij j

lkk

qq b b b a

This sum contains products of terms symmetric and antisymmetric with respect to the

indices

i and l , thus vanishing; it results

[

]

==, 0, , 1,2,...,

bb jk s.

(19.2.14')

As well,

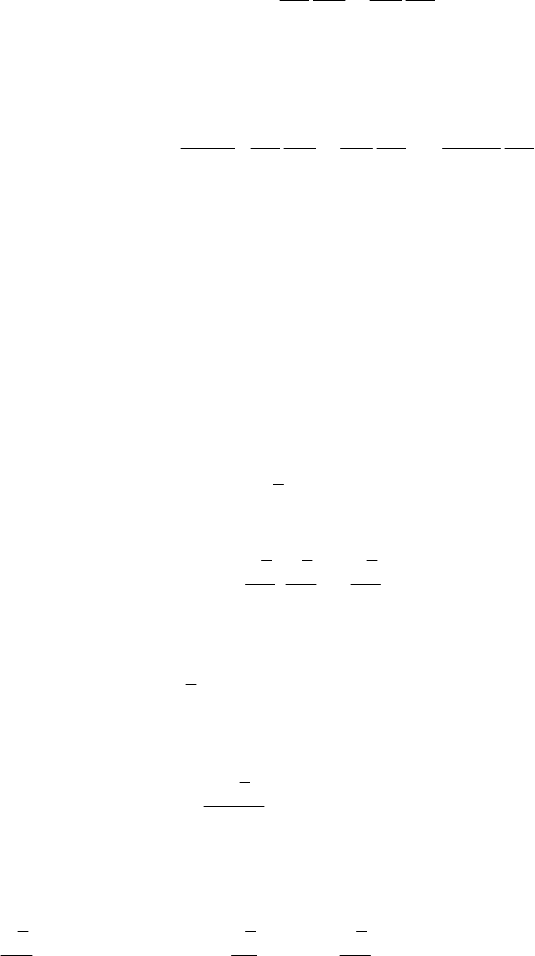
MECHANICAL SYSTEMS, CLASSICAL MODELS

166

[]

∂∂ ∂∂

=−

∂∂ ∂∂

ii ii

qp qp

ba ab

Replacing the partial derivative of the generalized momenta in the above Lagrange

bracket, one obtains

[]

∂∂

∂∂ ∂

∂∂

⎛⎞

=−+

⎜⎟

∂∂ ∂ ∂ ∂ ∂ ∂∂ ∂

⎝⎠

il il i

ij j i j

lkk k

qq q

qq b a a b qa b

Considerations analogue to those above show that the first sum vanishes; concerning

the second sum, we take into account the first relation (19.2.12'). We obtain

[

]

=δ =, , , 1,2,...,

kjk

bk jk s.

(19.2.14'')

Thus, all the Lagrange brackets which can be set up have been put in evidence.

19.2.1.4 Generalized Conservative Mechanical Systems. Cyclic Co-ordinates

In case of a generalized conservative mechanical system, hence for which

= 0H



one obtains a remarkable form of the Hamilton–Jacobi equation; indeed, in this case we

can write the first integral

=Hh, so that the equation in S reads +=0Sh



wherefrom the integral

()

=− +

, ,...,

ShtSqqq, one of the integration constants

being the energy constant

h . One obtains thus the reduced Hamilton–Jacobi equation

∂∂ ∂

⎛⎞

⎜⎟

∂∂ ∂

⎝⎠

, ,..., , , ,...,

SS S

Hqq q h

qq q

(19.2.15)

while the complete integral is given by

()

−

=− +

12 12 1

, ,..., ; , ,..., ,

ShtSqqqaaah.

(19.2.15')

The condition (19.2.6) becomes

∂

⎡⎤

≠=

⎢⎥

∂∂

⎣⎦

det 0,

(19.2.15'')

The solutions of the system of canonical equations will be given by the sequences of

relations

∂∂∂

== − =+ = =

∂∂∂

, 1,2,..., 1, , , 1,2,...,

SSS

bj s tb pk s

ahq

(19.2.15''')

The first

− 1s relations give the trajectory of the representative point in the

configuration space

Λ (hence, ==−( ), 1,2,..., 1

qqqj s), the subsequent

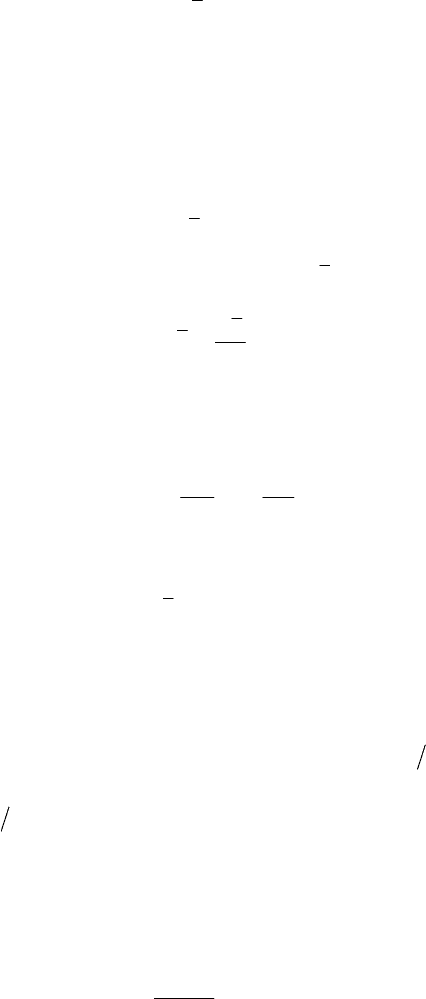
Hamiltonian Mechanics

167

relation specifying the motion on this trajectory (after replacing the previous results, we

get

= ()

qqt and, returning, we obtain ==−( ), 1,2,..., 1

qqtj s) . The last

relations show that the function

S is a simple potential for the generalized momenta,

which are – in this case – conservative.

As well, we see that the function

S plays the rôle of a simple quasi-potential for the

generalized momenta, which are thus quasi-conservative. Taking into account that the

complete integral is not unique, it results that this quasi-potential is not uniquely

determinate too (excepting an arbitrary constant, which appears in the usual case).

In case of a generalized conservative mechanical system, the wave surface (19.2.12)

is given by

=Sht.

(19.2.16)

At a given moment

consttt

, one obtains = constS ; we have

∂

ddd

Sqpq

If the constraints are scleronomic, the mechanical system being conservative (we have

= 0U



too), then we can write

∂

===−

∂∂

jjj

Tq qpq





so that

∫

STt

(19.2.17)

the representative point

P corresponding to the initial moment and the representative

point

being an arbitrary point in the configuration space

Λ . In this case, the

function

S is called action; it verifies the reduced Hamilton–Jacobi equation (19.2.15).

In case of

r cyclic co-ordinates

, hence for which

0, 1,2,...,Hq r

α∂∂ = =

the corresponding generalized momenta are constant (

, 1,2,...,pa r

αα

α== ); it

results

∂∂ =Sq a

αα

, so that the complete integral will be

()

∑

12 12

, ,..., ; ; , ,...,

SaqSqqqtaaa

αα

(19.2.18)

the conditions (19.2.6) being reduced to

∂

⎡⎤

≠

⎢⎥

∂∂

⎣⎦

det 0

jk r

(19.2.18')

MECHANICAL SYSTEMS, CLASSICAL MODELS

168

The Hamilton–Jacobi equation reads

∂∂ ∂

⎛⎞

⎜⎟

∂∂ ∂

⎝⎠

00 0

12 12

, ,..., , , ,..., , , ,..., ; 0

SS S

SHqq qaa a t

qq q



(19.2.18'')

corresponding to a canonical system in

−2( )sr variables (as it is known – as a matter

of fact – from the study of Hamilton’s system of equations). The sequences of relations

(19.2.10) become

∂∂

=− + = = = + +

∂∂

∂

== ==++

∂

, 1,2,..., , , 1, 2,..., ,

, 1,2,..., , , 1, 2,..., .

qb r bjr r s

pa r pjr r s

αα

(19.2.18''')

In case of a generalized conservative mechanical system, which has

r cyclic

co-ordinates, the function

will be of the form

()

++ −

=− + +

∑

12 12 1

, ,..., , , ,..., ,

rr s

Sht aqSqq qaaah

αα

(19.2.19)

and the reduced Hamilton–Jacobi equation becomes

∂∂ ∂

⎛⎞

⎜⎟

∂∂ ∂

⎝⎠

00 0

12 12

, ,..., , , ,..., , , ,...,

SS S

Hq q qaa a h

qq q

(19.2.19')

There result

∂

=− + =

∂

==++ −

∂

=+ = =

∂

==++

∂

,1,2,....,

, 1, 2,..., 1,

, , 1,2,.... ,

, 1, 2,..., .

qb r

bj r r s

tbp a r

pj r r s

αα

(19.2.19'')

19.2.1.5 Case of a Discrete System of Particles

Let be a discrete system

S of n particles, of masses

m , of velocities v

and of

momenta

==Hv, 1,2,...,

mi n. Assuming that this system is not subjected to

constrains, it results that

= 3sn and that we can choose as space of configurations the re-

presentative space

E . Using the corresponding notations (see Sect. 18.1.1.2), we can

introduce the generalized momenta

== =, 1,2...,3

kkkkk

PMVMXk n



(19.2.20)

Hamiltonian Mechanics

169

Assuming that the generalized forces

Q derives from a simple quasi-potential

()

12 3

, ,..., ;

UUXX Xt, the equation of motion (18.1.38) reads

∂

+===

∂∂

∑

, 1,2,...,3

PQkn

Xt X



;

we observe that this equation can be written also in the form

∂

⎡⎤

∂

⎛⎞

+−+−=

⎢⎥

⎜⎟

∂∂∂

⎝⎠

⎣⎦

∑∑

jjj

PPUP

XM MXX



If the generalized momenta derive from a quasi-potential

()

12 3

, ,..., ;

SSXX Xt,

then we find

⎡⎤

∂∂

⎛⎞

+−==

⎢⎥

⎜⎟

∂∂

⎝⎠

⎢⎥

⎣⎦

∑

0, 1,2,..., 3

SUkn

XMX



It results that the function between the square brackets depends only on the time

t ,

being of the form

()ft. If, instead of the quasi-potential S , we use the quasi-potential

−

∫

()dSftt, then we notice that the 3n generalized momenta are not influenced;

hence, we can write the equation of motion

∂

⎛⎞

+−=

⎜⎟

∂

⎝⎠

∑



(19.2.21)

As a matter of fact, observing that Hamilton’s function =−HTU is given by a

relation of the form (19.1.87'), we can also write

∂∂ ∂

⎛⎞

⎜⎟

∂∂ ∂

⎝⎠

12 3

, ,..., ; ; , ,..., 0

SS S

S HXX X t

XX X



(19.2.21')

obtaining thus the corresponding Hamilton–Jacobi equation.

Let us build up the Pfaff form of Hamilton

=−

∑

PX Htω .

(19.2.22)

This form is a total differential if and only if the relations

∂

=−= =

∂∂∂

, , . 1,2,...,3

Pjk n

XX X



hold. Taking into account the expression of Hamilton’s function, we can write

MECHANICAL SYSTEMS, CLASSICAL MODELS

170

∂

+=+=

∂∂∂

∑∑

kkk

PPPP

MX MXX



But

= dd

kk k

PM X t

, so that

∂

ttX

(19.2.23)

Hence, the existence of the quasi-potential

is connected to the existence of the

quasi-potential

U ; but this one is only a necessary condition for the existence of the

function

S , because some conditions concerning the initial state must be satisfied too.

Thus, at the initial moment

tt we must have

() , ()

jj j

Xt X Vt V==,

wherefrom

000

() , ()

Pt P Ut U== and =

()Ht H; because, in a problem of

Cauchy type, the equation of motion (19.2.23) must hold also at the initial moment, it

results that the Pfaff form of Hamilton

=−

∑

000

PX Htω

(19.2.22')

must be a total differential at the initial moment too. If this condition is also fulfilled,

then one can use the field description by means of the Hamilton–Jacobi equation.

Observing that

∂

∑

ddd

SXSt



we can write

=−

∑

ddd

SPXHt

(19.2.24)

too, where we take into account the Hamilton–Jacobi equation. Then

()

⎛⎞⎛⎞

=+=+=+

⎜⎟⎜⎟

⎝⎠⎝⎠

∑∑

11 1

dddd

jjj

S P Ut MV Ut TUt

Introducing the kinetic potential (18.2.34), we obtain

=ddStL .

(19.2.25)

We can write

−=

∫

SS tL

(19.2.25')