Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

Hamiltonian Mechanics

141

[]

()

[]

()

{}

[]

()

[]

()

{}

[]

()

[]

()

{}

[]

()

[]

()

{}

+=δ

∑

,, ,, ,

ij i ij i

kkjk

ij i ij i

kkjk

ij i ij i

kkjk

ij i ij i

kkjk

ξξ ξξ ηξ ηξ

ξξ ξη ηξ ηη

ξη ξξ ηη ηξ

ξη ξη ηη ηη

(19.1.53')

for

=, 1,2,...,jk n.

In case of a Hamiltonian system, let be the functions

= (, ;)

qptϕϕ ,

= (, ;)

qptψψ of class

C ; the corresponding Poisson’s bracket is

[]

∂

∂∂

∂∂∂∂

==−

∂∂∂∂∂

∂

∂∂

jjj

qp pq

ϕϕψψ

ϕψ

(19.1.54)

We mention the obvious properties

== = =

=− − =−

(,) 0,(, ) 0,( , ) (, ), const,

(, ) (, ),( , ) (, ),

CC CCϕϕ ϕ ϕψ ϕψ

ϕψ ψϕ ϕψ ϕψ

(19.1.55)

as well as the properties

∂∂

=− =− =

∂∂

( , ) , ( , ) , 1,2,...,

fq fp j s

(19.1.55')

===−=δ=( , ) 0, ( , ) 0, ( , ) ( , ) , , 1,2,...,

jjjj

kkkkjk

qq pp qp pq jk s.

(19.1.55'')

Starting from the relation of definition (19.1.54), it results, as well,

+= +

12 1 2

12 1 2 2 1

(,)(,)(,),

(,) (,) (,),

ϕϕψ ϕψ ϕψ

ϕϕ ψ ϕ ϕ ψ ϕ ϕ ψ

(19.1.55''')

where we have used the formulae of differentiation of the sum and of the product of

two functions. The formula of differentiation of a function of function leads to

∂

∑

(, ) ( , )

ϕψ ψ

(19.1.56)

∂∂∂∂

⎛⎞

=−

⎜⎟

∂∂ ∂∂

⎝⎠

∑∑

(, ) ( , )

QP PQ

ϕϕψψ

ϕψ

(19.1.56')

MECHANICAL SYSTEMS, CLASSICAL MODELS

142

where

= (,)

QPϕϕ , = (,)

QPψψ , with

12 1 2

( , ,..., , , ,..., ; ),

( , ,..., , , ,..., ; ), 1,2,..., .

QQqq qpp pt

PPqq qpp ptj m

We can calculate

()

∂∂ ∂∂

∂∂∂∂∂

=+−−

∂ ∂∂∂ ∂∂∂ ∂∂∂ ∂∂∂

∂∂∂∂∂∂∂∂

=−+−

∂∂ ∂∂ ∂∂ ∂∂

2222

jjj jjjj

jj jj jj jj

t tqp qtp tpq ptq

qp pq qp pq

ϕϕ ϕϕ

ψψ ψψ

ϕψ

ϕϕϕϕψψψψ



where we assume the continuity of the derivatives of second order and where the point

indicates the differentiation with respect to time; there results

∂

(, ) (, ) (, )

ϕψ ϕψ ϕψ



(19.1.57)

Introducing the differential operator

∂∂∂∂

=−

∂∂ ∂∂

jjj

qp pq

ϕϕ

(19.1.58)

where

∈

Cϕ

is a given function, we can express Poisson’s bracket in the form

()

=,D

ϕψ ψ.

(19.1.58')

Let be

= (, ;)

qptχχ ; we assume that the functions ,ϕψ and χ are of class

C .

Taking into account the expression of Poisson’s brackets in the form (19.2.58'), we can

write

()()()()

()

−=−=

∂∂∂∂∂∂∂ ∂∂ ∂ ∂∂

⎡

=+−−

⎢

∂∂∂∂ ∂∂∂∂ ∂∂∂∂ ∂∂∂∂

⎣

22 2

,, ,, DD DD D

jj j j jj j j

kk k k kk k k

qpqp qqpp qppq qppq

ϕϕ

ψψ

ϕψχ ψϕχ χ χ

ϕϕϕϕϕψψ ψ

∂∂∂∂∂∂ ∂∂ ∂∂ ∂∂

−−+ +

∂∂∂∂ ∂∂∂∂ ∂∂∂∂ ∂∂∂∂

∂∂ ∂

∂∂∂∂∂∂∂∂∂

⎛

−+−−

⎜

∂∂∂∂ ∂∂∂∂ ∂∂∂∂ ∂∂∂∂

⎝

∂∂ ∂∂∂∂∂∂

−−+

∂∂∂∂ ∂∂∂∂ ∂

2222

222

jj j j jj j j

kk k k kk k k

jj j j jj j j

kk k k kk k k

jj j j j

kk k k

pqqp pqqp pqpq ppqq

qpqp qqpp qppq qppq

pqqp pqqp p

ϕϕϕϕψψ ψψ

ϕϕ ϕ

ψψψψ

ϕϕψψψ

∂∂∂ ∂

⎞

⎤

⎟

⎥

∂∂ ∂ ∂ ∂ ∂∂

⎠

⎦

jjj

kk k k

qp q p p qq

ϕϕψ

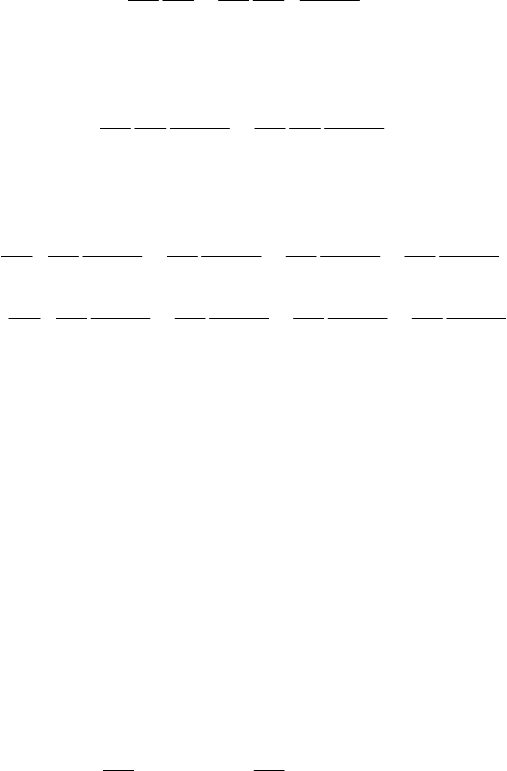
Hamiltonian Mechanics

143

Observing that the operators of second order are of the form

∂∂∂∂ ∂

⎛⎞

−=

⎜⎟

∂∂ ∂∂ ∂∂

⎝⎠

jjj

kkk

qq qq pp

ϕϕψψ

or of the form

∂∂∂∂ ∂ ∂

−+ =

∂∂∂∂ ∂∂∂∂

jj jj

kk kk

qppq pqqp

ϕϕψψ

the commutator D will be also an operator of first order; we remain with

()

∂∂ ∂ ∂ ∂

∂∂ ∂∂

⎛⎞

+−−

⎜⎟

∂∂∂∂ ∂∂∂ ∂∂∂ ∂∂∂

⎝⎠

∂∂ ∂ ∂ ∂

∂∂ ∂∂

⎛⎞

−+−−

⎜⎟

∂∂∂∂ ∂∂∂ ∂∂∂ ∂∂∂

⎝⎠

==−=−

2222

D(, ) D(, ) ,(, ).

jj jj jj jj

kkkkk

jj jj jj jj

kk k k k

qqqp qpp qpp pqp

ppqq qpq qpq pqq

χχ

χϕ ϕ ϕ ϕ

ψψ ψψ

χϕ ϕ ϕ ϕ

ψψ ψψ

ψϕ ϕψ χ ϕψ

Finally, we get the Poisson–Jacobi identity

()()()()()()

++=,, ,, ,, 0ϕψχ ψχϕ χϕψ .

(19.1.59)

As a matter of fact, in the left member of this identity one observes that each term will

have as factor a derivative of second order of one of the functions

,ϕψ

or χ . But all

the derivatives of second order of the function

χ vanish, as it has been shown; the

expression in the above identity is obtained by circular permutations of the first Poisson

bracket, so that the derivatives of second order of the functions

ϕ and ψ will be equal

to zero too, the identity being thus proved.

If we take

qϕ

pϕ

and = Hψ , we obtain (corresponding to the

formulae (19.1.55'))

() ()

∂∂

==−=

∂∂

, , , , 1,2,...,

qH pH j s

(19.1.60)

Hamilton’s equations (19.1.14) take the form

() ()

===, , , 1,2,...,

jj j j

qqHppHj s ,

(19.1.60')

used in the quantic modelling of mechanics.

MECHANICAL SYSTEMS, CLASSICAL MODELS

144

19.1.2.3 First Integrals of the Canonical System

Let be

= (, ;)

ffqpt a first integral of Hamilton’s canonical system, which is

constant along the trajectory of the representative point

∈

P Γ ; thus, we will have

∂∂

=++=

∂∂

ff f

qpf

tq p





Taking into account the equations (19.1.14), this necessary condition becomes

+=(, ) 0fH f



(19.1.61)

where we use Poisson’s bracket. As well, starting from the partial differential equation

of first order

∂∂ ∂∂

−+=

∂∂ ∂∂

jj jj

fH fH

qp pq



we can write the associate characteristic system (the Lagrange–Charpit sequence) in the

form (19.1.19), hence in the form of Hamilton’s equations. Hence, we can state

Theorem 19.1.5 (Poisson). The function

=∈

12 1 2

( , ,..., , , ,..., ; )

ffqq qpp ptC is a

first integral of the canonical system (19.1.14) only and only if the relation (19.1.61)

(which is thus a necessary and sufficient condition) holds.

= 0f



, hence if the function

does not depend explicitly on time ( = (, )

ffqp),

then the condition (19.1.61) becomes

=(, ) 0fH .

(19.1.61')

In the particular case

=fH we find again the first integral of the generalized

mechanical energy.

Performing the partial differentiation of the relation (19.1.61) with respect to time

and taking into account (19.1.57), we can write

++=(, ) (, ) 0fH fH f



; if = 0H



corresponding to a generalized conservative mechanical system; then we remain with

the relation

∂

(, ) 0



and we can state

Theorem 19.1.6 (Poisson). If

= (, ;)

ffqptis a first integral for Hamilton’s equations

of a generalized conservative mechanical system, then

, ,...ff



are, as well, first integrals

for this system.

If we make

= Hχ

in the Poisson–Jacobi identity, that one takes the form

++=( ,( , )) ( ,( , )) ( ,( , )) 0HHHϕψ ψ ϕ ϕψ ; assuming that

Hamiltonian Mechanics

145

+= +=(, ) 0,(, ) 0HHϕϕψψ



(19.1.62)

and taking into account the properties (19.1.55), (19.1.57), we can write

∂

(( , ), ) ( , ) 0H

ϕψ ϕψ

(19.1.62')

We state thus

Theorem 19.1.7 (Jacobi–Poisson). If we suppose that the functions

==∈

(, ;), (, ;)

jj jj

qpt qpt Cϕϕ ψψ are first integrals of the canonical system

(19.1.14), then Poisson’s bracket

(, )ϕψ is a first integral of the system.

Starting from the first integrals

,,H ϕψ, one can build up new first integrals of the

form

, ,..., , ,...,( , ),( , ),( ,( , )),( ,( , ))HH Hϕϕ ψψ ϕ ψ ϕ ϕψ ϕ ψ



etc., by means of the last

two theorems. Thus, one can obtain, at a given moment, a constant or a first integral

which is not independent on the previous first integrals; indeed, the canonical system

admits at the most

distinct first integrals.

If, by setting up a Poisson bracket of the first integrals

ϕ and ψ , we get

==(, ) , constCCϕψ

(19.1.63)

==(, ) (, ), constCCϕψ ϕψ ,

(19.1.63')

which is – practically – the same thing, then we say that the two first integrals are

canonically conjugate. Moreover, if, in particular,

=(, ) 0ϕψ ,

(19.1.64)

then we say that the first integrals

ϕ and ψ are in involution.

More general, let us consider the functions

12 1 2

( , ,..., , , ,..., ; )

ffqqqpppt

αα

= 1,2,...,rα ; after S. Lie, the set of these functions forms a functional group if

( , ) ( , ,..., ), , 1,2,...,

ff f ff f r

βαβ

αβ , hence if Poisson’s bracket of two

functions of this set is a function of the functions which belong to the set. These notions

have been used by S. Lie in the study of Hamilton’s system of equations.

19.1.2.4 Theorem of Lie. Theorem of Liouville

Let us suppose that

r first integrals =

12 1 2

( , ,..., , , ,..., ; )

ffqq qpp pt of the

canonical system are known, so that

+= =( , ) 0, 1,2,...,

fH f j r



(19.1.65)

Assuming that these first integrals are in involution, we can write

MECHANICAL SYSTEMS, CLASSICAL MODELS

146

≡=( , ) 0, , 1,2,...,

ff jk r.

(19.1.65')

Thus, the system of functions

={ , 1,2,..., }

fj r will be a system in involution.

Let us introduce the conjugate variables

p and =

qt, so that ∂∂=

/0Hp ,

∂∂= =

/ 0, 1,2,...,

fp j r. Let be, in general, the functions ϕ and ψ of variables

12 1 2

, , ,..., , , , ,...,

qqq qppp p. We can set up Poisson’s bracket

∂∂

=−+

∂∂ ∂ ∂

(, ) (, )

tp p t

ϕϕ

ψψ

ϕψ ϕψ ,

(19.1.66)

where we put the index zero so to specify the introduction of the variables

q and

p ; if

∂∂=∂∂=

//0ppϕψ , then we have =

(, ) (, )ϕψ ϕψ . Denoting

fHp

and

observing that

+= =

(, ) (, ) 0

jj j

ffH ff



, we can express the relations (19.1.65),

(19.1.65') in the unitary form

( , ) 0, , 1,2,...,

ff jk r.

(19.1.67)

We assume that the equations

== =, const, 1,2,...,

jjj

fcc j r, and +=

0Hp

lead to

==−=

12 1 2 12 2

( , ,..., , , ,..., , , ,..., ; ),

( , ,..., , , ,..., , , ,..., ; ) ,

rr s

pqqqpppccct

pH H qq qpp pcc ct

(19.1.68)

for = 1,2,...,kr. If u is one of the variables

12 1 2

, , ,..., , , , ,...,

qqq qpp p p,

then we can write

∂∂

∂

+==

∂∂∂

∑

0, 1,2,...,

upu

∂∂

∂−

∂∂∂

∑

()

,1,2,...,

upu

αα

We notice that these equations become identities if

u is one of the variable

, , ,...,

ppp p. We can thus write

∂−

∂∂

∂−

∂∂

∂∂ ∂ ∂ ∂ ∂

∑∑

()

, 0,1,2,...,

ii i i

qp p p q p

αα

ββ

αβ

Taking the double of the skew-symmetric part with respect to the indices

j and

, it

results

()

∂

=−−=

∂∂

∑∑

, ( , ) , , 0,1,2,...,

ff p p jk m

αα

ββ

αβ

ϕϕ .

(19.1.69)

Hamiltonian Mechanics

147

The conditions (19.1.67) read

()

∂

== −−

∂∂

∑∑

() ()

0, , ,

, , 0,1,2,..., .

zz pp

jk r

αα

ββ

αβ

ϕϕ

(19.1.67')

Fixing

k , one obtains a system of + 1r linear algebraic equations with

∂∂ ≠det[ / ] 0

, by the previous hypothesis; we get =

()

z , hence also a system

+ 1r linear algebraic equations with the same non-zero determinant of the

coefficients. Finally,

−−=(,)0pp

αα

ββ

ϕϕ

−−==

( , ) 0, , 0,1,2,...,

pp jk rϕϕ .

(19.1.70)

In an expanded form, we can write

()

∂∂

⎛⎞

=−

⎜⎟

∂∂ ∂∂

⎝⎠

∂

=− =

∂∂

∑

, , 0,1,2,..., .

qp pp

jk r

σσ σσ

ϕϕ

(19.1.70')

These conditions show that the functions

, ,...,

ff f are first integrals of the canonical

system, being two by two in involution.

Replacing

p by

ϕ , = 1,2,...,jr, −H by

ϕ and dt by

dq in the Pfaff form of

Hamilton (19.1.45), we obtain the form

==+

∑∑

qpq

σσ

ωϕ ,

(19.1.71)

the bilinear covariant of which is given by

== =+

=+ =+ = = =+

=+ =+ = =

∂∂

⎛⎞

′

=δ − = δ + δ

⎜⎟

∂∂

⎝⎠

∂∂

⎛⎞

∂

+δ− + δ

⎜⎟

∂∂∂

⎝⎠

∂

⎡⎛ ⎞

∂

−δ=−

⎜⎟

⎢

∂∂∂

⎣⎝ ⎠

∂

−

∂

∑∑ ∑

∑∑ ∑∑ ∑

∑∑ ∑ ∑

00 1

11 00 1

11 0 0

ddd

rs s

jk r

ss rs s

rr jk r

ss r r

rr k j

qqq

pq q p q

pqp

pq q

pqq

ρσ ρ

ρρ

σρ ρ

ρσ

σρ

ϕϕ

ωω ω

ϕϕ

=+ =+ =+ = =+

=+ = =+

∂

⎛

∂

⎤⎞

−δ+ −δ

⎜

⎟

⎥

∂∂∂

⎦⎠

⎝

∂

⎛

∂

⎞

++δ

⎜

⎟

∂∂

⎠

⎝

∑∑ ∑∑∑

∑∑ ∑

11 101

10 1

ddd

dd.

ss srs

rr rjr

sr s

qpq qpq

pqp

qqp

ρρ ρσ

ρσρ

ρρ σ ρ

σρ

ρρ

MECHANICAL SYSTEMS, CLASSICAL MODELS

148

The associate differential system, obtained by equating to zero the brackets which

multiply the differential variations

δq

and

δp

, is written in the form

∂∂

=− =− = + +

∂∂

∑∑

d d ,d d , 1, 2,...,

qqpqrrs

σσ

ϕϕ

(19.1.72)

The equations obtained by annulling the square brackets which multiply the differential

variations

q are identically verified if one takes into account the conditions (19.1.70')

and the equations (19.1.72). The functions

=, 0,1,2,...,

jrϕ , being thus determined,

the system (19.1.72) becomes a system of

−2( )sr equations with −2( )sr unknown

functions.

Corresponding to Morera’s method of integration, we introduce an arbitrary

parameter

λ , so that ==( ), 0,1,2,...,

qq j rλ . Denoting

++ ++

=−

∑

12 1 2 12 2

( , ,..., , , ,..., , , ,..., ; )

rr r r s

Kq q q p p p c c c

λϕ

(19.1.73)

the system of equation (19.1.71) reads

∂∂

′′

== ==− =++

∂∂

, , 1, 2,...,

qK p K

qp rrs

σσ

λλ

(19.1.72')

As a matter of fact, starting from the Pfaff form

=−

∑

pq K

σσ

ωλ

(19.1.71')

one obtains the same result. We can thus state

Theorem 19.1.8 (S. Lie). If the system of

2s canonical equations (19.1.14) admits

≤,rr s, first integrals in involution, resolvable with respect to r , of the generalized

momenta, then the integration of this system is reduced to the integration of a system of

−2( )sr canonical equations in −sr pairs of conjugate variables and to quadra-

tures.

The generalized co-ordinates

, ,...,

qq q are then determined, using the relation

∂

=− =

∂

, 1,2,...,

 .

(19.1.74)

In the particular case

=rs, we notice that ∂∂= =/ 0, , 0,1,2,...,

pjk sϕ , and

from (19.1.70') it results

∂

∂∂

, , 0,1,2,...,

jk s

(19.1.75)

Hamiltonian Mechanics

149

Thus, we can state that the existence (necessary and sufficient conditions) of a function

12 12

( , , ,..., ; , ,..., )

SSqqq qaa a is ensured, so that

∂∂

====− =

∂∂

, , 1,2,...,

SHjs

ϕϕ



(19.1.75')

Hence,

∂

∑∑

ddd

Sqq

(19.1.75'')

and we can state

Theorem 19.1.9 (Liouville). If the system of

2s canonical equations (19.1.14) admits

s first integrals in involution, resolvable with respect to the generalized momenta, then

the integration of this system is reduced to quadratures.

We notice that the function

S satisfies the partial differential equation of first order

∂∂ ∂

⎛⎞

⎜⎟

∂∂ ∂

⎝⎠

, ,..., , , ,..., 0

SS S

SHqq q

qq q



(19.1.76)

called the Hamilton–Jacobi equation, and the condition

∂

⎡⎤

=≠

⎢⎥

∂∂ ∂

⎣⎦

det det 0

qa a

(19.1.76')

assuming that the function

ϕ are resolvable with respect to the constant

=, , 1,2,...,

ajk s; in this case, S is the complete integral of the Hamilton–Jacobi

equation (see Sect. 19.2.1.1 too).

===0, 0, 1,2,...,

Hf j s



, hence if the Hamiltonian and the first integrals do

not contain explicitly the time, then the functions

ϕ have the same property, so that

12 12 12 12 12

( , ,..., , , ,..., ; ) ( , ,..., , , ,..., ) ( ; , ,..., )

ss ss s

SqqqaaatSqqqaaa taaaT .

From (19.1.75'), it results



T ; but (19.1.75) shows that

, consthhϕ =− = ,

obtaining

=− +ShtS.

Let be a generalized conservative mechanical system (

= 0H



), the canonical

system (19.1.14) of which admits

− 1s independent first integrals

=−, 1,2,..., 1

fj s , in involution, which do not contain explicitly the time

(

= 0



). The s th first integral is H and the other first integrals must verify the

conditions

( , ) 0, 1,2,..., 1

fH j s== −; hence, H is also in involution with these

first integrals and we can apply Liouville’s theorem.

MECHANICAL SYSTEMS, CLASSICAL MODELS

150

If, in case of the motion of a heavy rigid solid about a fixed point, beside the first

integral of the moment of momentum and the first integral of the kinetic energy we can

set up a third integral, in involution with the first two ones, then the integration of the

equations of motion is reduced to quadratures, according to Liouville’s theorem.

19.1.2.5 Other Formulations in the Spaces

Λ and

We have built up the Lagrangian formalism in the space

Λ to study the motion of

the representative point

P , while in the space

Γ we have used the Hamiltonian

formalism to determine the motion of the corresponding representative point; but these

formalisms are not the only ones which can be used.

For instance, starting from the relation (19.2.15'), we notice that one can write

()

⎡⎤

δ−=δ+δ

⎢⎥

⎣⎦

jjjjj

pq q p q p

L

too. Denoting

()

=−

ϕ L ,

(19.1.77)

we obtain

∂∂

===

∂∂

, , 1,2,...,

qqj s

ϕϕ



(19.1.77')

hence, relations of the form (19.1.13); one obtain thus, easily, a system of differential

equations of second order

∂∂

⎛⎞

−==

⎜⎟

∂∂

⎝⎠

0, 1,2,...,

tp p

ϕϕ



(19.1.77'')

analogue to Lagrange’s equations (the place of the generalized co-ordinates is taken by

the generalized momenta). But, to can set up the function

ϕ , we must solve the system

of equations (19.1.13) with respect to

q and

, function of

p and

p

, which is

difficult – in general – this system being non-linear in the generalized co-ordinates.

We can start also from the relation

()

δ−=δ−δ

jjjjj

qp q p p qL

We denote

=−

qpψ  L

(19.1.78)

and obtain the system of equations

∂∂

==−

∂∂

ψψ



(19.1.78')