Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

Hamiltonian Mechanics

121

We can calculate the first variation of the Lagrangian in the form

∂∂

δ= δ+ δ=δ+δ

∂∂

jjjjj

q q pq pq

 



(19.1.15)

which represents the sixth form of the basic equation; taking into account the operator

relation (18.1.77), this relation takes the remarkable form

()

δ= δ

(19.1.15')

in case of holonomic constraints. We can also write

()

δ−=δ−δ

jjjjj

pq q p p qL .

For Hamilton’s function, we obtain, analogically,

∂∂

δ= δ+ δ

∂∂

Using the relation of definition of Hamilton’s function and comparing these results, we

find again the canonical equations (19.1.14).

Hamilton’s equations form a system of

differential equations of first order in the

unknown functions

===( ), ( ), 1,2,...,

jj j j

qqtpptj s. Taking into account the

one-to-one link between the generalized velocities and the generalized momenta, we

can put the initial conditions in the form

() , ()

jj j

qt q pt p

(19.1.14')

Hence, we must know the position

P of the representative point P at the initial

moment. The number of the unknowns and of the equations became double, but their

order diminished by a unity, which represents a great advantage from the point of view

of computation; we remark also some properties of symmetry of the system of

equations (19.1.14).

We can write Hamilton’s equations in the matric form

=RZH



(19.1.14'')

too, where

[]

12 1 2

, ,..., , , ,..., ,

qq q pp p

12 12

, ,..., , , ,...,

HH HHH H

qq qpp p

∂∂ ∂∂∂ ∂

⎡⎤

⎢⎥

∂∂ ∂∂∂ ∂

⎣⎦

(19.1.14''')

are column matrices, respectively, and

Z is the matrix

MECHANICAL SYSTEMS, CLASSICAL MODELS

122

⎡

⎤

⎢

⎥

−

⎣

⎦

(19.1.14

)

The matrices

0 and I are the null and the unit matrices, respectively, with s rows and

s columns.

If, in Donkin’s theorem, we take

=XT, =

xq , , 1,2,...,

ypj s== , so that

the generalized momenta are given by

=∂ ∂ =/ , 1,2,...,

pTqj s , while the function

=Y Φ is specified by

=−

pq TΦ  ,

(19.1.16)

then we obtain Hamilton’s equations in the form

∂∂

==−++=

∂∂

, , 1,2,...,

jj jj

qp QRjs

ΦΦ





(19.1.16')

corresponding to a non-natural and non-holonomic mechanical system, hence to

Lagrange’s equations (18.2.32). If

, 1,2,...,

Qj s= , is the non-conservative part of

the generalized force, then Hamilton’s equations read

∂∂

==−++=

∂∂

, , 1,2,...,

jj jj

qp QRjs





(19.1.16'')

In case of holonomic constraints (

, 1,2,...,

Rj s= ) and of quasi-conservative forces

which derive from a simple potential (

0, 1,2,...,

Qj s==

) we find again the

canonical equations; in case of a generalized potential appears a supplementary term

due to the modality in which the generalized momenta have bean introduced. The

advantage to introduce these quantities by the relations (18.2.80) is thus put in

evidence; as a matter of fact, we can thus consider the case of an arbitrary Lagrangian

too.

19.1.1.4 General Theorems. First Integrals

For the initial value problem (19.1.14), (19.1.14') one can state

Theorem 19.1.2 (of existence and uniqueness; Cauchy–Lipschitz). If Hamilton’s function

H is of class

C with respect to the space variables and of class

C with respect to time

on the (

+21s )-dimensional interval D , specified by −≤≤+

00 00

jjjjj

qQ qqQ,

−≤≤+

00 00

jj jjj

pP ppP, −≤≤+

00 00

tTttT, ==

, , const, 1,2,...,

QPT j s,

and defined in the space Cartesian product of the phase space (of canonical co-ordinates

12 1 2

, ,..., , , ,...,

qq qpp p) by the time space (of co-ordinate t ), and if Lipschitz’s

conditions

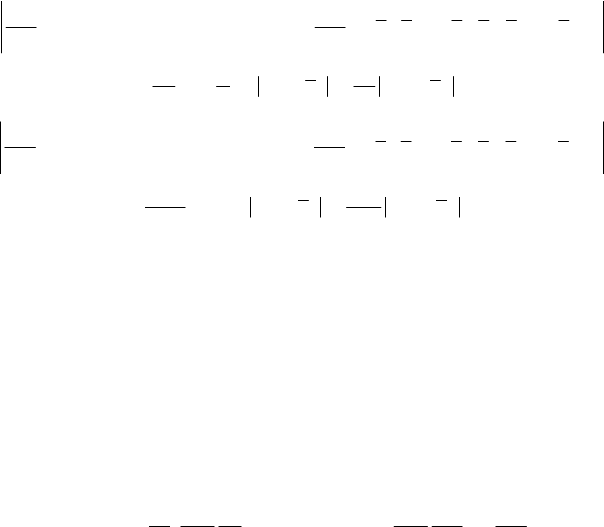
Hamiltonian Mechanics

123

∂∂

−

∂∂

⎡⎤

≤−+−

⎢⎥

⎣⎦

∑

12 1 2 12 1 2

( , ,..., , , ,..., ; ) ( , ,..., , , ,..., ; )

ss ss

kk k k k

Hqq qpp pt Hqq qpp pt

qq pp

τλ

∂∂

−

∂∂

⎡⎤

≤−+−

⎢⎥

⎣⎦

∑

12 1 2 12 1 2

( , ,..., , , ,..., ; ) ( , ,..., , , ,..., ; )

ss ss

kk k k k

Hq q q p p p t Hq q q p p p t

qq pp

νμλ

hold for

= 1,2,...,

, where > 0T is a time constant independent on

q ,

p and t ,

the time constant

τ and the constant μ of the nature of a mass are equal to unity,

while

λμν are constants equal to unity (dimensionless if the corresponding

generalized co-ordinate is a length and having the dimension of a length if the

corresponding generalized co-ordinate is non-dimensional), then there exists a unique

solution

==(), ()

jj j j

qqtppt of the system (19.1.14), which satisfies the initial

conditions (19.1.14') and is definite an the interval

−≤≤+

tTttT

, where

⎡⎤

∂∂

⎡

⎤

≤=

⎢⎥

⎢

⎥

∂∂

⎣

⎦

⎣⎦

min , , , , max ,

jjjj

TTj

ττ

λλ

μλ μλ

TV D

without summation with respect to the index

j .

The continuity of the derivatives of first order of the function

H with respect to the

canonical co-ordinates on the interval

D ensures the existence of the solution,

according to Peano’s theorem. Lipschitz’s conditions must be also fulfilled for the

uniqueness of the solution; but the latter conditions can be replaced (as in the case of

other theorems of uniqueness) by other ones less restrictive, according to which the

partial derivative of second order of the function

H with respect to the canonical co-

ordinates must exist and must be bounded in absolute value on the interval

D . As a

matter of fact, the conditions in the Theorem 19.1.2 are sufficient conditions of

existence and uniqueness, which are not necessary too.

As in the case of other analogous theorems (e.g., the Theorem 18.2.1) one can obtain

a prolongation of the solution for

∈

[, ]ttt, corresponding to a certain interval of

time in which the considered phenomena takes place, or even for

∈∞

[,)tt or

∈∞

(, ]tt or ∈−∞∞(,)t .

We can state also theorems on the continuous or analytical dependence of the

solution on a parameter, analogue to the Theorems 6.1.3 and 6.1.4; as well, we state

Theorem 19.1.3 (on the differentiability of the solution). If, in the neighbourhood of a

point

∈

12 1 2

( , ,..., , , ,..., ; )

qq qpp ptPD, the functions ∂∂/

Hq, ∂∂/

Hp,

= 1,2,...,js, =

12 1 2

( , ,..., , , ,..., ; )

HHqq qpp pt, are of class

C , then the solution

MECHANICAL SYSTEMS, CLASSICAL MODELS

124

()

qt and ()

pt of the system (19.1.14) which satisfy the initial conditions (19.1.14')

are of class

+1k

C in a neighbourhood of the point P .

We call first integral of the system of canonical equations (19.1.14) a function

12 1 2

( , ,..., , , ,..., ; )

ffqq qpp pt of class

, which is reduced to a constant along

the integral curves (trajectories in the phase space)

===

12 2 12 2

( ; , ,..., ), ( ; , ,..., ), 1,2,...,

jj j j

q q tc c c p p tc c c j s,

(19.1.17)

of this system (

=, 1,2,...,2

ck s, are, obviously, integration constant); hence

∂∂

=++=

∂∂

dd dd0

fq pft



(19.1.18)

∂∂

=++=

∂∂

ff f

qpf

tq p





(19.1.18')

along the integral curves.

The canonical equations (19.1.14) can be written in the form

==== = == =

∂∂ ∂ ∂ ∂ ∂

−− −

∂∂ ∂ ∂ ∂ ∂

12 1 2

dd d d

ddd

... ...

qq p p

qpt

HH HHH H

pp p q q q

(19.1.19)

too, for integration being necessary

2s independent first integrals. If we determine

≤ 2ls first integrals

== =

12 1 2

( , ,..., , , ,..., ; ) , const, 1,2,...,

kkk

fqq qpp pt cc k l,

(19.1.20)

the matrix

∂

⎡

⎤

⎢

⎥

∂

⎣

⎦

12 1 2

( , ,..., )

( , ,..., , , ,..., )

ff f

qq qpp p

being of rank

, then all these integrals are functionally independent (independent first

integrals) and we can express

l unknown functions of the system (19.1.19) with respect

to the other ones; replacing in this system of equations, the problem is reduced to the

integration of a system of equations with

−2sl unknowns (hence, with a smaller

number of unknowns). If

= 2ls, then all the first integrals are independent, so that the

system (19.1.20) determines all the unknown functions. We notice that, if

> 2ls

, then

the first integrals (19.1.20) are no more independent; hence, one can set up at the most

2s independent first integrals.

Hamiltonian Mechanics

125

Solving the system (19.1.20) for

= 2ls, we obtain (the matrix M is a square one of

order

2s , for which ≠Mdet 0 ) the solution (19.1.17), hence a general integral of the

system of equations (19.1.14). One puts thus in evidence

2s integration constants.

Imposing the initial conditions (19.1.14'), it results

12 2

( ; , ,..., )

qtcc c q= ,

12 2

( ; , ,..., )

ptcc c p= , = 1,2,...,js; the conditions (19.1.14') being independent,

we may write

∂

⎡⎤

≠

⎢⎥

∂

⎣⎦

00 000 0

12 1 2

12 2

( , ,..., , , ,..., )

det 0

( , ,..., )

qq qpp p

cc c

and we get

00 000 0

01 2 1 2

( ; , ,..., , , ,..., )

cctqq qpp p= , 1,2,...,2ks= , using the theorem

of implicit functions.

Thus, it results, finally (for = 1,2,...,js),

00 000 0

12 1 2

00 000 0

12 1 2

( ; , , ,..., , , ,..., ),

( ; , , ,..., , , ,..., ).

qqttqq qpp p

ppttqq qpp p

(19.1.21)

Hence, in the frame of the conditions of the theorem of existence and uniqueness, the

canonical equations and the corresponding initial conditions determine, univocally, the

motion of the discrete mechanical system S , subjected to holonomic ideal constraints,

in a finite interval of time; by prolongation, the statement can be valid for any

t . The

deterministic aspect of mechanics is thus put in evidence in the Hamiltonian

presentation too.

fc and =

fc are two distinct first integrals, then =

(, ) 0ff f is a first

integral too; any other first integral is expressed, in general, as a function of the

distinct first integrals of Hamilton’s equations.

19.1.1.5 Hamilton’s Function

Starting from the relation of definition (19.1.11), passing to canonical co-ordinates,

taking into account (18.2.80), (18.2.34') and using Euler’s theorem concerning

homogeneous functions, we can write Hamilton’s function in the form

∂

=−= −=+−=−

∂

21 2

jj j

Hpq q









LLLLLLL

If we take into account also the relations (18.2.34''), it results

==−+

,HTTV



(19.1.22)

where



is the generalized mechanical energy, given by (18.2.68) and expressed in

canonical co-ordinates (

=−VU in case of a simple quasi-potential or =−

VU in

case of a generalized quasi-potential). In case of a scleronomic mechanical system

MECHANICAL SYSTEMS, CLASSICAL MODELS

126

(

0, 0TT



) we have

=+=+=

TVTVE



, obtaining the mechanical

energy of the considered mechanical system.

Observing, on the basis of the formulae (18.2.15') and (19.1.1'), that

−−+ −+

=−+ −+

2[()][()]

[ ( )][ ( )],

jl km

mmm

jk l l l

jjj

kkk

Tggp gUgp g U

gp g U p g U



we can represent Hamilton’s functions in the form

=++

HH H H,

(19.1.23)

where

== =− +

=++−+

22 1

,(),

()() ,

jk jk

jjj

HT gppH ggUp

HggUgUgV

(19.1.23')

hence a sum of a quadratic form, of a linear form and of a constant with respect to the

generalized momenta. In case of scleronomic constraints we have

0g ,

==0, 1,2,...,

gj s, so that

=− = +

jk jk

HgUpHgUUV,

(19.1.23'')

and in case of generalized forces which derive from a simple potential it result

= 0

U ,

= 1,2,...,js, so that

=− = − +

jk jk

HggpH ggggV;

(19.1.23''')

if both conditions are fulfilled, then

0,HHV.

=δ

kjk

g , then we have =δ

g , where δ

is Kronecker’s tensor; we can

write

=δ = = =δ =

222

11 1 1

22 2 2

jj j j j

jk k jk k

TqqqqHTpppp 

(19.1.24)

hence in the form of a sum of squares. In this case, the generalized co-ordinates are

orthogonal (they are called normal co-ordinates), the generalized momenta having the

same property.

We can calculate

∂∂

=++

∂∂

HH H

qpH

tq p





Hamiltonian Mechanics

127

Taking into account the equations (19.1.14), we can state that the relation

∂



(19.1.25)

takes place along the integral curves of Hamilton’s system of equations. If Hamilton’s

function does not depend explicitly on time ( =



, hence





), then the

generalized mechanical energy

12 12 12 12

( , ,..., , , ,..., ) ( , ,..., , , ,..., ) ,

ss ss

Hqqqppp qqqppph==E const,h =

(19.1.26)

is a first integral of the canonical system (19.1.14). This first integral corresponds to

Jacobi’s first integral or to a first integral of Jacobi type of Lagrange’s system of

equations, which can be written if

= 0



(see Sect. 18.2.3.4); as a matter of fact,



leads to = 0



and reciprocally, on the basis of the last relation (19.1.12').

The mechanical system is, in this case, a generalized conservative system (as in the case

in which

= 0



). If the mechanical system is scleronomic, then we find again the first

integral of the mechanical energy expressed in canonical co-ordinates

( =+==

HTVEh



), as a particular case; we have to do with a simple or

generalized potential (

= 0U



) in this case, so that ∂− ∂+∂∂=

()/ /0TT t Vt



We notice that to have

= 0H



it is not necessary that the mechanical system be

scleronomic. Indeed, from (19.1.23') we see that it is necessary and sufficient to have

=+==

0, 0,

ggUgV



 

;

(19.1.27)

the first relations above lead also to

= 0

g for

, 1,2,...,

, Taking into account

(18.2.15'), (18.2.15''), we can state that these relations can take place only and only if

the derivative

∂∂ =r / , , 1,2,...,

qij s, do not depend explicitly on time, i.e. if

′′′

rrr

iii

′′

( , ,..., )

qq q ,

′′ ′′

rr( ), 1,2,...,

ti s. This statement remains

valid for Jacobi’s first integral or for the first integrals of Jacobi type too; in particular,

for

′′

r ,1,2,...,

is0 , when the mechanical system is scleronomic, then one obtains

the integral of mechanical energy.

19.1.1.6 Reduction of the Number of First Integrals

As we have seen above, the function

H is a first integral of the canonical system of

equations if

= 0H



; hence, it is necessary to determine other −21s first integrals. If

we write Hamilton’s equations in the form (19.1.19), then we notice that – in this case –

we can neglect the last ratio in this system; indeed, to integrate the remaining system of

equations, there are sufficient

−21s first integrals, which do not depend explicitly on

time. Thus we can determine

−21s canonical co-ordinates as functions of one of

them. To fix the ideas, we assume that

∂∂≠

/0Hp ; we find thus the generalized co-

MECHANICAL SYSTEMS, CLASSICAL MODELS

128

ordinates

−

112 21

( ; , ,..., ), 2,3,...,

qqqcc c j s, and the generalized momenta

−

112 21

( ; , ,..., ), 1,2,...,

ppqcc c i s. In this case, it results the function of

Hamilton

−

112 21

( ; , ,..., )

HHqcc c , where we have put in evidence the integration

constants. From the first and the last ratio (19.1.19) we get

−

∂

⎛⎞

=+=

⎜⎟

∂

⎝⎠

∫

12 112 2

d ( ; , ,..., )

tqcFqccc

(19.1.28)

the function

F containing he last integration constant

c too. Observing that the

derivative

−

∂∂=∂∂ ≠

/(/)0Fq Hp , the theorem of implicit functions allows to

calculate

1112 2

( ; , ,..., )

qqtcc c. Introducing then in the above results, we obtain the

general integrals (19.1.17).

The system of equations (19.1.19) is of the form (15.1.24), so that one can use the

theory of Jacobi’s multiplier (see Sect. 15.1.1.4), as well as the theory of the last

multiplier (see Sect. 15.1.1.5). In this case,

xq,

sj j

xp, =∂ ∂/

XHp,

=−∂ ∂ =/ , 1,2,...,

sj j

XHqj s, and

x , =+21ns. We notice that the

divergence of the vector which has as components the denominators in (19.1.19)

vanishes

()

∂∂ ∂∂ ∂∂

⎛⎞ ⎛⎞

⎛⎞

+++

⎜⎟

⎜⎟ ⎜⎟

∂∂ ∂∂ ∂∂

⎝⎠

⎝⎠ ⎝⎠

∂∂ ∂∂ ∂∂ ∂

⎛⎞ ⎛⎞

⎛⎞

+−+ − ++−+ =

⎜⎟

⎜⎟ ⎜⎟

∂∂ ∂∂ ∂∂ ∂

⎝⎠

⎝⎠ ⎝⎠

11 22

...

... 0,

HH H

qp qp qp

HH H

pq pq pq t

hence the condition (15.1.30) is fulfilled; a constant is thus a multiplier of the sequence

of equations (19.1.19), while – according to the Theorem 15.1.4'' – any non-constant

multiplier is a first integral of this system of differential equations. Hence, there are

sufficient

−21s first integrals to determine the general solution of the respective

system. If

= 0H



, then there remain sufficient −22s first integrals for a complete

study of the canonical equations. For instance, in case of the problem of two particles –

at a first view – there are necessary

⋅=26 12 first integrals; according to what has

been shown above, in case of scleronomic mechanical systems and of conservative

forces there are sufficient

⋅−=2(6 1) 10 first integrals. If the two particles are

subjected to no one constraint, being acted upon only by forces of Newtonian attraction,

we are just in the mentioned case; the conservation theorem of momentum leads to six

first integrals, the conservation theorem of the moment of momentum allows to write

three first integrals and the conservation theorem of mechanical energy given also a

first integral, so that the integration of the corresponding system of canonical equations

is reduced to quadratures.

Let be a scleronomic conservative Hamiltonian system with two degrees of freedom.

It is possible, in this case, to write the integral of the mechanical energy, i.e.

===

1212

(,, , ) , constHqqpp hh ; one obtains the differential system

Hamiltonian Mechanics

129

== = =

∂∂ ∂ ∂

−−

∂∂ ∂ ∂

12 1 2

dd d d

qq p p

HH H H

pp q q

Let us suppose that another first integral ==

12 1 2

(, ; , ) , constfq q p p cc , which does

not contain explicitly the time, is known. The two first integrals being independent, we

can calculate

(, ;,), 1,2

ppqqhcj

; replacing in Hamilton’s equations, this

system is reduced to

∂∂

with the unknown functions ==(), 1,2

qqtk , for which the last multiplier

=∂ ∂

det[ ( , )/ ( , )]Mpphc satisfies the equation (see Sect. 15.1.1.5 too)

∂∂

⎛⎞⎛⎞

∂∂

⎜⎟⎜⎟

∂∂

⎝⎠⎝⎠

∂∂

Hence,

∂∂

⎛⎞

−=

⎜⎟

∂∂

⎝⎠

∫

ddconst

Mq q

is a first integral of the last differential system. We notice that

H and f depend on h

and

c by means of the generalized momenta

p and

p . Because =d/d 1Hh and

=d/d 0Hc , it results

∂∂ ∂∂

+= +=

∂∂ ∂∂ ∂∂ ∂∂

12 12

1, 0

pp pp

HH HH

ph ph pc pc

One obtains analogous results from

=d/d 0fh , =d/d 1fc . The determinant M

being non-zero, we can write

∂∂

==−

∂∂∂ ∂

∂∂

==−

∂∂∂ ∂

pcp c

php h

The last first integral becomes

∂

==+

∂

∫

12 1 1 2 2

const, ( , ; , ) ( d d )qqhc pq p q

MECHANICAL SYSTEMS, CLASSICAL MODELS

130

Then, taking into account

∂∂ =

det[ ( , )/ ( , )] 1MHfpp, the reduced system of

differential equations allows to write

∂∂

⎛⎞

=−

⎜⎟

∂∂

⎝⎠

ddd

tM q q

wherefrom

∂

constt

The integration of the differential system is thus reduced to a quadrature, which

determines the function

χ .

19.1.1.7 Routh’s Equations

It is convenient, in some cases, to use as parameters which describe the motion of the

mechanical system

S a part of the Hamiltonian co-ordinates and a part of the

Lagrangian ones; one obtains thus a “mixed method” to approach the problem. We

assume that the motion is specified by Hamilton’s variables (denoted by Greek indices)

=, , 1,2,...,qp r

αα

α and Lagrange’s variables (denoted by Roman indices) ,

qq ,

=+ +1, 2,...,jr r s, the set of which form Routh’s variables. We effect a partial

Legendre transformation of the form

∂

, 1,2,...,pr



(19.1.29)

which allows to determine

12 1 2 1 2

(, ,,;)

( , ,..., , , ,..., , , ,..., ; ), 1,2,..., .

sr s

qqqpqqt

qqq qpp pq q qt r

αα

ββ

 



Applying a variation

δ to Lagrange’s function = (,,,;)

qqqqt

αα

LL , we obtain

==+

∂∂ ∂∂

⎛⎞

δ= δ+ δ + δ+ δ

⎜⎟

∂∂ ∂∂

⎝⎠

∑∑

qq qq

αα



LL LL

Taking into account (19.1.29), we notice that

== =

∂

δ=δ+δ

∂

∑∑ ∑

11 1

rr r

pq q q p

αα α α α

αα α





wherefrom

== =+

∂∂∂

⎛⎞

δ−=−δ−δ− δ+δ

⎜⎟

∂∂∂

⎝⎠

∑∑ ∑

11 1

rr s

pq q q p q q

qqq

αα α α α

αα

 



LLL