Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

Lagrangian Mechanics

101

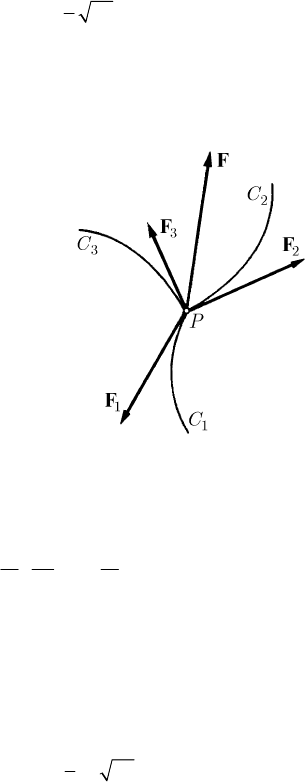
If the intersections of the surfaces

= const

q and = const

q taken two by two are

the curves

≠≠,

Ci j ≠≠ki, =,, 1,2,3ijk (Fig. 18.9), then the element of arc on

these curves is given by

()

dd!,1,2,3

iii

sAqi ,

(18.3.40)

so that

ddd

sss.

(18.3.39'')

Fig. 18.9 Elliptic co-ordinates in

The kinetic energy is calculated in the form

()

==++

222

11 22 33

2d 8

ms m

T AqAqAq

,

(18.3.41)

allowing thus to obtain Lagrange’s equations. We decompose the given force

F along

the tangents to the curves

123

,,CCC

, hence let be

=++FF F F

123

; the

corresponding virtual work will be

⋅δ = δ = δFr

ii ii

Qq Fs. Taking into account

(18.3.40), it results

()

!, 1,2,3

iii

QFAi .

(18.3.42)

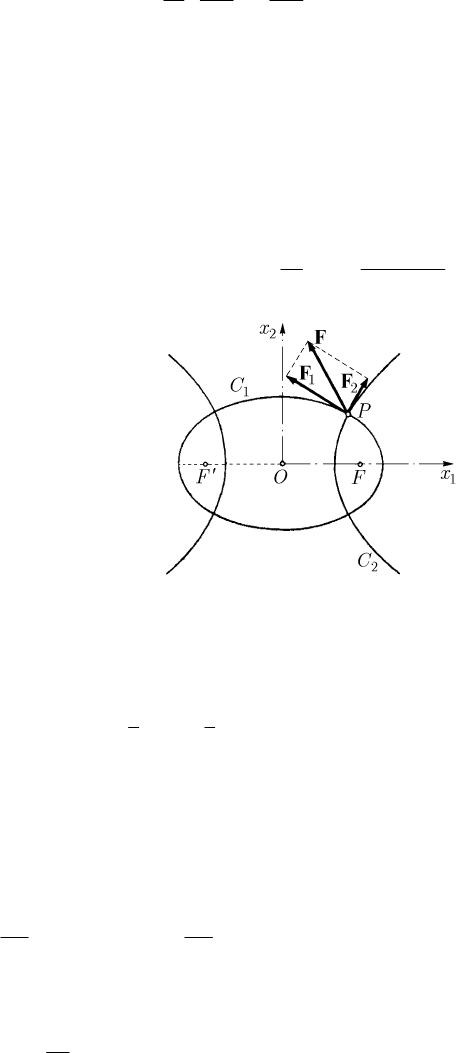
In case of a plane motion, we can use elliptic co-ordinates in the plane

Ox x

, the

corresponding formulae being obtained by particularization (we make

0, 0xq==)

from the above ones. The homofocal conics will be an ellipse and a hyperbola (Fig. 18.10).

If the given forces are conservative or quasi-conservative, then we can use the results

in Sect. 18.1.1.3 concerning natural systems.

Lagrange’s equations can be written also in the vector form

MECHANICAL SYSTEMS, CLASSICAL MODELS

102

′′

∂∂

⎛⎞

−=

⎜⎟

∂∂

⎝⎠

(18.3.43)

with respect to a non-inertial frame of reference

R (the generalized co-ordinates are taken

with respect to this frame); in this case, the kinetic energy is given by

′′

=+++

vv r

(/2)( )

Tm ω . We notice that

′

is a known function of time and

can be expressed as the total derivative with respect to time of another function; hence,

this term can be omitted from calculation (Lagrange’s function – inclusive the kinetic

energy – is determined excepting the total derivative with respect to time of an arbitrary

function). On the other hand, we notice that

()

′

⋅

⎡

⎤

′′ ′

⋅+×= ⋅= −⋅

⎢

⎥

⎣

⎦

vv r v ar

OO O

mmm

;

Fig. 18.10 Elliptic co-ordinates in

the total derivative with respect to time can be, as well, neglected. Thus, we can use the

conventional kinetic energy

()

′

=+⋅×−⋅

vvrar

Tm m m



ω .

(18.3.44)

We can calculate

() ()

[]

′

=+×⋅− +×+××⋅

vrva v rrdd d

Tm m



ωωωω,

wherefrom

() ()

[]

∂∂

′

=+× =− +×+××

∂∂

vr a v r



ωωωω.

(18.3.44')

The equation (18.3.43) leads thus to the equation of motion

()

[]

′

=− +×+× × − ×

Fa r r v

mm m



ωωω ω,

(18.3.45)

Lagrangian Mechanics

103

written with respect to the non-inertial frame of reference

R ; the transportation force

and the Coriolis force are thus put in evidence (see Sect. 10.2.1.1 too)

18.3.2.2 Case of a Particular Conservative Force

We consider the motion of a particle P acted upon by a conservative force which

derives from the simple potential

=++

222

() ()

(,, ) ()

sin

Ur fr

θϕ

(18.3.46)

expressed in spherical co-ordinates. Noting that

=∂ ∂/

QUr, =∂ ∂/QU

θ and

=∂ ∂/QU

ϕ , we obtain Lagrange’s equations in the form

()

⎡

⎤

′

−+ = − +

⎢

⎥

⎣

⎦

222

322

()

sin ( ) ( )

sin

rr fr g

mr r

θθϕ θ



 

()

⎡

⎤

′

−=−

⎢

⎥

⎣

⎦

22 2

224

d2sin2

2sin2 ()()

sin

rr g h

mr r

θθϕ θϕ



(18.3.47)

()

′

()

sin

θϕ

 ,

where we have denoted by “prime” the derivative of the functions

and , fg h with

respect to the corresponding variables.

The third equation (18.3.47) can be written also in the form

()

22 22 442

sin sin d sin ( ) d ( )d d ( ),

mr r r h t h hθϕ θϕ θϕ ϕ ϕ ϕ ϕ ϕ

′′

====

  

so that we obtain the first integral

[]

442

sin ( )rhC

θϕ ϕ ,

(18.3.48)

where

C is an integration constant; as well, the second equation (18.3.47) reads

()

2442

24 4

d1 sin2 2 sin2

2()sin(),

sin sin

rg r h

mr mr

θθ

θθ θϕϕ

θθ

⎡⎤

′

−= −=

⎢⎥

⎣⎦



where we took into account the first integral previously found. Multiplying by

r θ



, one

obtains

() ( )

()

⎡

⎤

′

== +

⎢

⎥

⎣

⎦

⎡⎤

=−

⎢⎥

⎣⎦

22 42

2sincos

2d d ()d2 d

sin

() d ,

sin

rr r g tC t

θθ

θθ θ θθ θ

  

MECHANICAL SYSTEMS, CLASSICAL MODELS

104

resulting the first integral

⎡

⎤

=++

⎢

⎥

⎣

⎦

()

sin

rg C

θθ



(18.3.48')

where

C is a new integration constant. Eliminating the terms

rθ



and

sinr θϕ

between the first equation (18.3.47) and the first integrals (18.3.48), (18.3.48'), we

obtain

′

−=

2()

rfr



Multiplying by

drt and integrating, we get the third first integral

[]

+= +

22()

rfrC

 ,

(18.3.48'')

where

is a new integration constant. As a matter of fact, one can obtain this result

starting from the first integral of the mechanical energy and taking into account the first

integrals previously obtained.

The first integral (18.3.48'') contains only one space variable, so that

⎡

⎤

=± = − +

⎢

⎥

⎣

⎦

11 3

(), () 2() 2

fr fr fr C

(18.3.49)

wherefrom, by a quadrature, one gets

t as a functions of r and then = ()rrt,

introducing the fourth integral constant

C . Analogously, the first integral (18.3.48')

leads to

⎡

⎤

=± = − +

⎢

⎥

⎣

⎦

dd 2

,() ()

sin

() ()

gg C

rfr g

θθ

(18.3.49')

By two quadratures, we obtain

= ()rθθ and then = ()tθθ, a new integration

constant

C being introduced. Finally, the first integral (18.3.48) allows to write

[]

=± = +

dd 2

,() ()

() sin ()

hhC

ϕθ

ϕϕ

ϕθθ

(18.3.49'')

where we have used the previous result; hence, one obtains

= ()ϕϕθ and then one

gets

= ()tϕϕ , appearing the integration constant

C .

The integration constants

=, 1,2,...,6

Ck , are then determined by means of the

initial conditions.

The case of loading of a particle

P , considered above, is useful in many particular

cases of great interest.

Lagrangian Mechanics

105

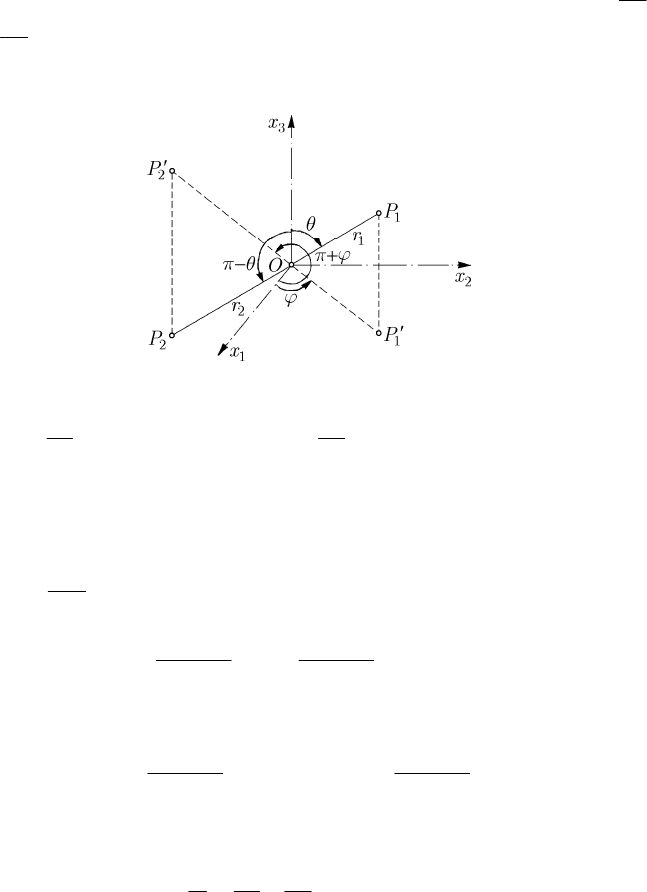
18.3.2.3 Problem of Two Particles

Let be two particles

P and

P of masses

m and

m , ≥

mm, respectively; the

mass centre

O is on the segment of a line

PP , so that ==

11 22 1

,mr mr r OP ,

=≤

212

,rOPrr (Fig. 18.11). In spherical co-ordinates, we have

(,,)Prθϕ ,

−+

(, , )Prπθπϕ, and the kinetic energy can be expressed in the form

Fig. 18.11 Problem of two particles

()()

=++ +++

222222 222222

11 1 22 2

sin sin

Trrr rrrθθϕ θθϕ





We introduce the notations

+= +=

222222

11 22 11 22

,mr mr mr mr mr mr, with

rr r

(18.3.50)

where

rPP; we get

12 12

rrrr

mm mm

so that

+= +=

12 12

22 222 2

11 22 11 22

12 12

mm mm

mr mr r mr mr r

mm mm

 .

Comparing with the notations which have been introduced, we must have

111

mm m

(18.3.50')

Thus, the motion of relation about the mass centre

O is specified by the generalized co-

ordinates

===

123

,,qrq qθϕ, corresponding to three degrees of freedom. The

kinetic energy will be thus given by

MECHANICAL SYSTEMS, CLASSICAL MODELS

106

()

=++

222222

sin

Tmrr r

θθϕ





(18.3.51)

Assuming that the two particles are acted upon only by forces of Newtonian

attraction, the potential function being

(18.3.51')

we obtain the case considered in the preceding section, with

() /fr fmm r and

==() ( ) 0ghθϕ; the problem is thus reduced to quadratures.

18.3.2.4 Problem of Two Centres

Let be a particle subjected to the attraction of two fixed centres

C and

C , in an

inverse proportion to the squares of the distances

==,1,2

rPCk , to these centres;

the potential of the corresponding forces is

(18.3.52)

where

,0kk are positive constants. We can study this problem in spherical co-

ordinates too, by means of the results obtained in Sect. 18.3.2.2.

But we can study the problem also with the aid of the elliptical co-ordinates

introduced in Sect. 18.3.2.1. If, in this order of ideas, we denote

() ()

== + == −

112212

qrrqrr

λμ,

(18.3.53)

then the curves

= constλ represent ellipses, the semi-major axes of which are equal to

λ , and the curves = constμ are hyperbolae the semi-major axes of which are equal to

μ ; these curves are homofocal (they have common foci

C and

C ) and orthogonal

one to the other. Observing that

+= −= =

12 12 12

min( ) 2 , max 2 , 2rr c rr ccCC, it

results the relation of condition

≥≥cλμ; in this case, the equations of the families

of ellipses and hyperbolae will be

+=+=

−−

22 22

12 12

222 222

1, 1

xx xx

λλ μ μ

(18.3.54)

By logarithmic differentiation, we can calculate the kinetic energy in the form

()()

⎛⎞

=+=− +

⎜⎟

−−

⎝⎠

22 22

22 2 2

Txx

λμ





(18.3.55)

Taking into account (18.3.53), we obtain the potential

Lagrangian Mechanics

107

()()

[]

=+−−

−

12 12

Ukkkk

λμ

(18.3.55')

observing thus that we have a system of Liouville type (see Sect. 18.3.1.2). Because

==−

=+ =−

11 22

11 1 2 22 1 2

() , () ,

() ( ), () ( ),

uq uq

Uq k k Uq k k

λμ

==−

−−

11 22

22 22

22 2 2

() , () ,

d,d,

Vq Vq

Wm Wm

λμ

=− = =−

,, ,u λμααα α

the system of equations (18.3.7) leads to

−=

−=+

∫∫

() ()

(),

() ()

ϕλ ψμ

λμ β

ϕλ ψμ

(18.3.56)

with the notations

=− ++ +

=− +− +

22 2

() ( )[ ( ) ],

ch k k

ϕλ λ λ λ α

ψμ μ μ μ α

(18.3.56')

where

h is the constant of mechanical energy, while and

,αβ β are three other

integration constants.

We denote by

and

12 12

,,λλ μμ pairs of two simple roots, differing from ±c , of the

equations

=() 0ϕλ and =() 0ψμ , respectively, and let be the integrals

∫∫

11 12

21 22

() ()

λμ

ωω

ϕλ ψμ

ωλ ω μ

ϕλ ψμ

(18.3.57)

We introduce also the quantities

and

νν by relation

+= +=+

11 1 12 2 1 21 1 22 2 2

,()tων ων πβ ων ων π β .

(18.3.58)

The relations (18.3.56) define thus

andλμ as double periodical (elliptic) functions of

and

t β or (with the relations (18.3.58)) of and

νν. If a relation of the form

MECHANICAL SYSTEMS, CLASSICAL MODELS

108

+= ∈

111 212 1 2

0, ,nn nnωω ` , takes place, hence if and

11 12

ωω are commensurable

quantities, then the motion is strictly periodic with the period

121 222

22( )Tn nωω. If

the roots

and

12 12

,,λλ μμ, respectively, are double, then we have so called motions of

libration (called periodical conditioned motions too), important in the classical quantum

theory.

18.3.2.5 Motion of an Electrized Particle in an Electromagnetic Field

Let be an electrized particle P of electric charge q (eventually, an electron), which

is in motion with the velocity

v in an electromagnetic field EB{, }, where E is the

intensity of the electric field and

B is the magnetic induction (see Sect. 18.1.1.4).

Lorentz’s generalized force (18.1.36) derives from the generalized quasi-potential

(18.2.37'). We obtain thus Lagrange’s kinetic potential

=+⋅−vAv

()

mq A

(18.3.59)

where

=AA

123

(,, ;)xxxt is the vector magnetic quasi-potential, while the scalar one

123

(,, ;)AAxxxt. If one observes that =+ =d/d , 1,2,3

iii

vmvqAiL ,

then Lagrange’s equations (18.3.38) read

()

+= − ==

,0,

0, 1,2, 3

ii jji i

mv qA q v A A i

We assume that the velocities do not depend on the point but only on the time.

Calculating the total derivative

=∂ ∂ +d/d ( / )

iijji

At AxvA, Lagrange’s

equations become

()

=−−−=

⎡⎤

⎣⎦

,, 0,

,1,2,3

ji ij j i i

mqAAvAAi



(18.3.60)

The relations (18.1.36') and (18.1.36'') can be scalarly written in the form

=∈ = − + =

,( ),1,2,3

iiii

ijk k j

BAEAAi



It is seen that the equations (18.3.60) represent, in fact, the projections on the three

axes of co-ordinates of Newton’s equation of motion

()

=+×

EvB

(18.3.60')

where we have Lorentz’s generalized force (18.1.36); for this, one takes into account

the above relations and the relation

()

×=∈ =∈ ∈

=− =−

ijk k ijk klm m li

mim j ji ijj

il jl m l

vB v A

vA A A v

δδ δ δ

Lagrangian Mechanics

109

To take into account the relativistic aspect of the problem, one must introduce the

mass

=−

1(/)mm vc, where

m is the mass at rest, while c is the velocity of

propagation of light in vacuum.

18.3.2.6 Motion of the Rigid Solid

A free rigid solid S has six degrees of freedom and we can use, e.g., the

generalized co-ordinates

′

==,1,2,3

qxi , =

q ψ , =

q θ , =

q ϕ , where

′

are the co-ordinates of a point

O of it with respect to an inertial frame of reference

′

R , while ψ , θ and ϕ are Euler’s angles, which specify the rotation about the point

O . If a certain point

P of the solid is compelled to slide (without friction) on a given

surface, then it will have only two degrees of freedom, appearing thus a holonomic

constraint relation; analogously, if the point

P is compelled to stay on a given curve,

then there result two holonomic constraint relations. Especially, if to the point

P is

imposed a given motion, then the rigid solid is subjected to three holonomic constraints;

in particular, the point

P (taken – in this case – as a pole O of a non-inertial frame

R ) can be fixed. In each of these cases, one searches convenient generalized co-

ordinates, by eliminating the respective constraints; thus, in case of a rigid solid with a

fixed point, we can choose as generalized co-ordinates Euler’s angles, the kinetic

energy being of the form (15.1.13), where

123

,,III are the principal moments of

inertia with respect to the fixed point. We notice that

ψ is a hidden co-ordinate, so that

′

∂

⎛⎞

⎜⎟

∂

⎝⎠



(18.3.61)

For instance, in case of the motion of a heavy homogenous rigid solid of revolution

of mass

M , which slides frictionless on a fixed horizontal plane (see Sect. 17.1.2.4),

the kinetic energy reads

[]

{

}

22 2 2 22

12 3

()() sin(cos),

TM Mf JJ I

ρρ θ θ ψ θ ϕψθ

′′′′

=++++ ++





 

(18.3.62)

where

′′

,ρρ and

′

()fρθ are the co-ordinates of the mass centre

with respect to the

inertial frame of reference

′

R and where

JI I

; the potential of its weight is

=− ()UMgfθ .

(18.3.62')

We can use thus the generalized co-ordinates

′′

=====

11223 4

,,,,qqqqqρρϕψθ.

The first four equations of Lagrange are written in the form (

and

′′

,,ρρψ ϕ are hidden

and ignorable co-ordinates)

′ ′′′

∂ ∂∂∂

⎛⎞

⎛⎞ ⎛⎞

⎛⎞

= ===

⎜⎟

⎜⎟ ⎜⎟

⎜⎟

′′

∂∂∂

⎝⎠ ∂

⎝⎠ ⎝⎠

⎝⎠

d ddd

0, 0, 0, 0

d ddd

T TTT

t ttt

ρρϕ





MECHANICAL SYSTEMS, CLASSICAL MODELS

110

being thus led to the first integrals

′′′′

==+=

′

++ =

00 0

12 3

,,cos,

sin ( cos )cos ,

JI K

ρνρνϕψθω

ψθ ϕψθθ



 





(18.3.63)

where we have used the notations in Sect. 17.1.2.4. Instead of the fifth equation of

Lagrange, we can use the first integral of mechanical energy, the problem being thus

entirely formulated.

An important case is that of the rigid solid for which three non-collinear points have

a given motion in a fixed (or mobile) plane; the problem is thus reduced to the motion

of a mechanical system in a plane (or of a plane solid rigid), which has only three

degrees of freedom, corresponding to the translation of a point (two degrees of

freedom) and to the rotation about this point (one degrees of freedom).

In the case of a system of rigid solids, one must keep in mind the connections

between them. E.g., a hinge between two rigid solids involves the introduction of three

holonomic constraints (we can imagine a free rigid solid, the second one having a point

with a given motion).

18.3.2.7 Plane Motion of a Rigid Straight Bar

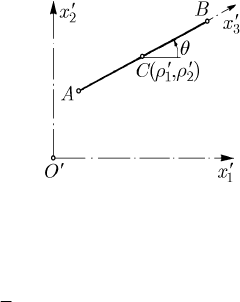
Let be a rigid straight bar AB which moves frictionless in the plane

′′′

Oxx , being

acted upon by forces in direct proportion to the mass and to the distance to the

′′

Ox -axis (we have chosen a system of particular forces, to fix the ideas). The position

of the bar is specified by the co-ordinates

′

ρ and

′

ρ of the mass centre C and by the

angle

made with the fixed axis

′′

Ox (Fig. 18.12); we can thus choose the

generalized co-ordinates

′′

===

11223

,,qqqρρθ.

Fig. 18.12 Plane motion of a straight rigid bar

Using Koenig’s theorem, we can write the kinetic energy in the form

()

′′′

=++

⎡

⎤

⎣

⎦

22 2

TM I

ρρ θ





(18.3.64)

where

M is the mass of the bar and I is its moment of inertia with respect to the

centre of mass

C .

Let us consider a bar element

dx along the Cx -axis, which is attracted by the

′′

Ox -axis by the force

(sin)d, constkxxkμρ θ

′

−+ =

, where μ is the linear