Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

Lagrangian Mechanics

so that

∂

∂∂

(2)

qq

(18.3.20')

as well as

∂

∂∂

(2)

qq

(18.3.14')

Taking into account these results, we obtain

(2)

11 1 1

223,

nn n n

ii i i

ii ii ii ii

jj j j

ii i i

mm m m

qqqqq

== = =

∂

∂∂∂

∂

⎛⎞

=⋅+⋅=⋅+⋅

⎜⎟

∂∂∂∂∂

⎝⎠

∑∑ ∑ ∑

  

arv

av a v

so that the relation (18.2.19') leads to

∂∂

⎧⎡ ⎤ ⎫

⎛⎞

−+δ=

⎨⎬

⎜⎟

⎢⎥

∂∂

⎝⎠

⎩⎣ ⎦ ⎭

∑



(18.3.22)

Because, in case of holonomic constraints, the variations

q of the generalized

accelerations are independent, we can write the equations of I. Tsenov in the form

∂∂

⎛⎞

−= =

⎜⎟

∂∂

⎝⎠

3 2 , 1,2,...,

Qj s



(18.3.23)

Taking into account the previous relations, we find easily that

()

∂∂∂∂

⎡⎤

⎛⎞

−= − =

⎜⎟

⎢⎥

∂∂∂∂

⎝⎠

⎣⎦

1d d

3 2 , 1,2,...,

jjjj

TT TT

qqqtq

 

(18.3.24)

Hence, the equations obtained in 1962 by Tsenov are equivalent to Nielsen’s equations

(hence, to Lagrange’s equations too), in the case of ideal holonomic constraints

(Dolapčev, Bl., 1966).

18.3.1.7 The Mangeron–Deleanu Equations

Starting from the expression of the derivative

d/dTt, we observe that

=⋅+⋅

=⋅+⋅+

∑∑

aa va

(2) (3)

(3) (4)

4 ...,

ii ii

MECHANICAL SYSTEMS, CLASSICAL MODELS

where, in the last expression, we have mentioned only terms which contain generalized

accelerations till



(and not generalized accelerations of higher order); by complete

induction, one can show that

−

=⋅+⋅+

∑∑

aa va

(1) ()

...

ii ii

mm m

(18.3.25)

where the terms which contain the generalized accelerations

()

q have been put in

evidence. On the other hand, starting from (18.3.21) and using the operator relation

(18.2.13), we obtain

∂∂

=+ +

∂∂

(3)

4 ...



 

and, in general, by complete induction,

∂∂

=+++=

∂∂

() ( 1) ()

( 1) ..., 1,2,...,

mm m

ij j

qmq i n

(18.3.26)

wherefrom

∂∂

==+==

∂∂

() ()

(1) ()

, ( 1) , 1,2,..., , 1,2,...,

iii i

minjs

(18.3.26')

We can thus calculate

−

∂∂

∂

⎛⎞

=⋅+⋅+

⎜⎟

⎝⎠

∂∂∂

∂∂

=⋅++⋅+=

∂∂

∑∑

(1) ()

() () ()

...

( 1) ..., 1,2,..., .

ii ii

mmm

jjj

ii ii

mm m

qqq

mm m m j s

(18.3.25')

The relation

()

⎡⎤

∂∂∂∂

⎛⎞

⎢⎥

−+ = −

⎜⎟

∂∂ ∂

⎝⎠

⎢⎥

∂

⎣⎦

()

1d d

(1) 2

TTTT

mt qqtq



(18.3.24')

which generalizes the relation (18.3.24) is thus easily stated. Thus, we find the

D. I. Mangeron–D. Deleanu equations (Lagrange’s generalized equations), obtained in

1962 in the form

∂∂

⎛⎞

−+ = = ∈

⎜⎟

∂

⎝⎠

∂

()

( 1) , 1,2,..., ,

mmQjsm

(18.3.27)

Lagrangian Mechanics

These equations are equivalent to Lagrange’s equations, to Nielsen’s equations and to

Tsenov’s equations, which result as particular cases for

= 1m and = 2m ,

respectively.

Let us consider a differential principle of the form

−−

⋅δ = ⋅δ ∈

∑∑

aa Fa

(1) (1)

ii i

mm` ,

(18.3.28)

where we have put in evidence accelerations of higher order; assuming that this

principle takes place for a given positions, a given velocity and given accelerations till

the

−(2)m -th order inclusive, at a fixed moment, varying only the accelerations of the

−(1)m -th order, we can write

−

∂

δ= δ=δ = ∈

∂

(1)

() () ()

()

, 1,2,..., ,

mmm

ijj

qqinm

` .

(18.3.26'')

The differential principle (18.3.28) can be written in the form

∂∂

⎛⎞

⋅− ⋅ δ= ∈

⎜⎟

∂∂

⎝⎠

∑

()

iii

mqm

` .

(18.3.28')

Starting from this principle we can obtain the Mangeron–Deleanu equations.

Obviously, in this case, the ideal constraints are defined by the relation

−

⋅δ = ∈

∑

(1)

qm`

(18.3.29)

All the equations thus established can be used for holonomic mechanical systems,

immaterial from the type of ideal constraints which are considered, which represents an

interesting generalization from the mechanical point of view. In case of non-holonomic

constraints, these equations are completed with constraint generalized forces, after

Lagrange’s method; one uses the equations which correspond to different types of ideal

constraints.

18.3.1.8 Case of a Non-inertial Frame of Reference

If we report the discrete mechanical system S to a non-inertial frame of reference

R (movable with respect to an inertial frame

′

R , considered fixed), then the

generalized co-ordinates

=, 1,2,...,

qj s

, will specify its position with respect to this

frame; as a matter of fact, the position of the system

S is thus specified even with

respect to the frame

′

R , because the motion of the frame R with respect to the

frame

′

R is known. One uses Lagrange’s equations (18.2.29) in the form

′′

∂∂

⎛⎞

−= =

⎜⎟

∂∂

⎝⎠

, 1,2,...,

Qj s

tq q

(18.3.30)

MECHANICAL SYSTEMS, CLASSICAL MODELS

where the kinetic energy with respect to the frame

′

R is given by

()

′′

=++×

∑

vv r

iii

Tm ω ,

(18.3.30')

being the velocities relative to the frame R , while = (,;)

QQqqt are the

generalized forces; because

=rr(;)

qt, one obtains

′′

(,;)

TTqqt , the problem

being then reduced to that corresponding to an inertial frame.

Another method of calculation is based on the theory of relative motion (see Sect.

10.2.1); one introduces thus the generalized forces

() ()

(,;)

QQqqt and

() ()

( , ; ), 1,2,...,

QQqqtj s , corresponding to the transportation generalized

forces and to the Coriolis generalized forces, respectively. Lagrange’s equations

become

∂∂

⎛⎞

′′

−= =++ =

⎜⎟

∂∂

⎝⎠

() ( )

, , 1,2,...,

jj j

QQ Q Q Q j s

tq q

(18.3.31)

where

= (,;)

TTqqt is the kinetic energy given by (calculated in the frame R )

∑

Tm.

(18.3.31')

Gilbert elaborated in 1883 a mixed method, which is based – partially – on the

theory of relative motion; one introduces thus a frame

R with the origin at the pole O

and with the axes parallel to the axes of the frame

′

R (which is not rotating about this

frame). Hence, Lagrange’s equations read

∂∂ ∂

⎛⎞

−=+ =

⎜⎟

∂∂ ∂

⎝⎠

, 1,2,...,

jj j

TT U

Qj s

tq q q



(18.3.32)

where

= (,;)

UUqqt

is a potential given by

′′

=⋅=−⋅

∑

ra a

Um Mρ ,

(18.3.32')

corresponding to the centrifugal force. The kinetic energy

= (,;)

TTqqt with respect

to the frame

R is given by (see Sect. 11.2.2.2)

()

=+×=++⋅

∑

vr K

ii i

Tm TI

ωωω,

(18.3.32'')

Lagrangian Mechanics

where

and T are the moment of momentum with respect to the pole O and the

kinetic energy, respectively, in the frame

R , while I

is the moment of inertia of the

mechanical system

S with respect to the instantaneous axis of rotation Δ ; thus, the

kinetic energy

T with respect to the generalized co-ordinates and the generalized

velocities is easily obtained. Using this method, Gilbert studies the influence of the

rotation of the Earth on the motion of a heavy rigid solid of revolution, fixed at a fixed

point

O (different from C ), the principal axis of inertia

Ox being in rotation in a

vertical plane linked to the Earth; the apparatus by which Gilbert verified

experimentally the results theoretically obtained is called barogyroscope.

18.3.1.9 The Phenomenon of Collision

In case of a phenomenon of collision, we start from the theorem of momentum,

written in the form (13.1.8) for a particle

of the discrete mechanical system S

subjected to constraints; a scalar product by

∂∂r /

q leads to

∂∂∂∂

′′ ′

⋅− ⋅=⋅+⋅

∂∂∂∂

rrrr

vvPP

iiii

ii ii i

jj j

qqqq

the position of the system

S remaining the same before and after collision (we

denoted by “second” the corresponding quantities after collision). Taking into account

the relations (18.2.28) and summing for all the particles of the system

S , we get the

jump relations

′′ ′

∂∂∂

⎛⎞⎛⎞⎛⎞

Δ≡−=+=

⎜⎟⎜⎟⎜⎟

∂∂∂

⎝⎠⎝⎠⎝⎠

, 1,2,...,

jjj

TTT

qqq

PP ,

(18.3.33)

where we have introduced the given generalized percussions and the constraint

generalized percussions, respectively, in the form

∂∂

=⋅ = ⋅ =

∂∂

∑∑

, , 1,2,..,

Rj Ri

(18.3.33')

the index zero corresponding to an arbitrary moment of discontinuity

′′′

∈

[, ]ttt,

′′ ′

−< >||,0tt

εε arbitrary.

Starting from the equations (18.2.32), integrating on the interval

′′′

[, ]tt

and passing

to the limit in the sense of the theory of distributions, we can write

′′ ′′ ′′

′′′

′′ ′ ′′ ′ ′′ ′

−→+ −→+ −→+

∂∂

⎛⎞

−=+

⎜⎟

∂∂

⎝⎠

∫∫∫

00 00 00

lim d lim d lim ( )d

ttt

tt tt tt

tQRt

qq

;

noting that

∂∂/

Tq is a finite quantity and neglecting the given and constraint non-

percussive forces with respect to the corresponding percussive ones, we find again the

jump relations (18.3.33), with

MECHANICAL SYSTEMS, CLASSICAL MODELS

′′ ′′

′′

′′ ′ ′′ ′

−→+ −→+

′′

′

′′ ′

−→+

∂

=⋅

∂

∂∂

=⋅ =⋅=

∂∂

∫∫

∑∑

∫

00 00

lim d lim d

lim d ,

tt tt

ii j

Qt t

and similar relations for the constraint generalized percussions.

Introducing the generalized momenta (18.2.80), considering Lagrange’s equations in

the form (18.2.36) and observing that

∂∂/

Uq is a finite quantity, one can write the

jump relations (18.3.33) in the form

()

′′ ′

Δ =−=+ =

, 1,2,...,

jjjj

ppp j sPP

(18.3.33'')

We state thus

Theorem 18.3.1 (theorem of generalized momentum). The jump of the generalized

momentum of a discrete mechanical system subjected to constraints, corresponding to a

generalized co-ordinate at a moment of discontinuity, is equal to the sum of the given

and constraint generalized percussions, which correspond to the same generalized

co-ordinate and which act upon the same system at that moment.

This theorem corresponds to the Theorem 13.1.2 stated in the space

Let us consider, in general, the case of a mechanical system

S subjected to

holonomic constraints, the position of which at the moment

′

is definite by the

generalized co-ordinates

′′ ′

, ,...,

qq q (after eliminating the holonomic constraints); at

the moment

′′′

∈

[, ]ttt,

new holonomic constraints are suddenly introduced, so that

the motion of the system

S is suddenly perturbed. while at the moment

′′

the

generalized velocities have finite variations, passing from

′′′

=,1,2,...,

qqj s , the

position of the considered system remaining practically the same. The preceding

constraints of the system

S are permanent, while the new introduced constraints can

become permanent or can disappear after the interval of percussion. The new

introduced constraints are expressed by relations of the form

( , ,..., ) 0, 1,2,...,

qq q l hϕ . Making a change of variable by which one replaces

the co-ordinates

q by the co-ordinates =

r ϕ , the new constraints imposed to the

system

S will be expressed in the form

==−+−+0, 1, 2,...,

rlshsh s

; we

assume to choose the generalized co-ordinates just in this form, having

−+ −+

===

0, 0,..., 0

sh sh

qq q. If the new constraints introduced are temporary,

then these co-ordinates will no more be equal to zero after the moment

′′

t ; otherwise,

they remain equal to zero. The arbitrary virtual generalized displacements

−

δδ δ

, ,...,

qq q

take place, while the virtual generalized displacements

−+ −+

δδ δ

, ,...,

sh sh

qq q

must vanish. We remain with Lagrange’s equations

∂∂

⎛⎞

−= = −

⎜⎟

∂∂

⎝⎠

, 1,2,...,

Qj sh

tq q

(18.3.34)

Lagrangian Mechanics

for the interval of percussion, the constraints generalized forces new introduced

disappearing from the calculation, because the corresponding virtual work vanishes

−+ −+ −+ −+

δ+δ++δ=

11 22

... 0

sh sh sh sh

Rq Rq Rq.

(18.3.34')

Noting that the variations of the generalized velocities are due only to the constraint

generalized forces, the intensity of which has increased very much but which have

disappeared from the calculation in the considered system of generalized co-ordinates,

it results that

∂∂/

Tq and

Q are finite quantities; by integration on the interval of

percussion and by passing to the limit, we find the jump relations

′′ ′

∂∂∂

⎛⎞⎛⎞⎛⎞

Δ≡−==−

⎜⎟⎜⎟⎜⎟

∂∂∂

⎝⎠⎝⎠⎝⎠

0, 1,2,...,

jjj

TTT

jsh

qqq

(18.3.34'')

which are linear and homogenous with respect to the differences

′′ ′

−=, 1,2,...,

qqj s . One can thus state that the generalized momenta corresponding

to the generalized co-ordinates, which do not vanish at the moment of collision, have

the same values before and after this phenomenon (have not a jump). The generalized

co-ordinates

, ,...,

qq q have such values, in the equations (18.3.34''), that

−+ −+12

, ,...,

sh sh

qq q do vanish at the moment of collision. In exchange, the generalized

velocities

−+ −+12

, ,...,

sh sh

qq q  must not necessarily vanish, neither before, nor after

collision; they equate to zero after collision if the new introduced constraints are permanent.

In this last case, the relations (18.2.34'') determine entirely the generalized velocities

−

′′ ′′ ′′

, ,...,

qq q  , hence the state of generalized velocities after collision. Beside this

particular case, we have at our disposal only

−sh

equations for s unknown generalized

velocities, so that we must make supplementary hypotheses for the mathematical modelling

of the mechanical phenomenon.

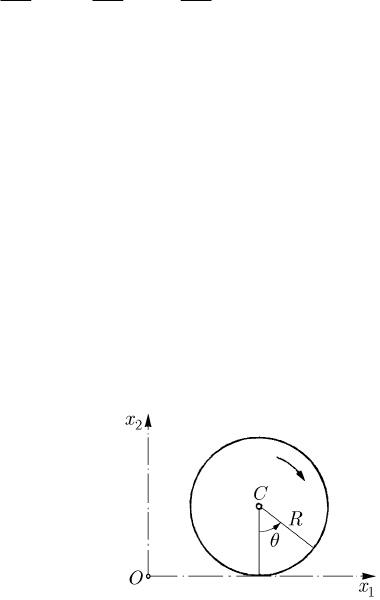
Fig. 18.8 A circular disc rolling without sliding on an axis in a vertical plane

As Beghin and Rousseau have shown in 1903, in case of a non-holonomic

mechanical system, the constraint generalized forces are finite, so that they disappear

from calculation, as well as the given generalized forces; hence, in this case, the jump

relations (18.3.34'') can be applied too.

Let be, e.g., a homogenous circular disc, of mass

M and radius R , which moves in the

vertical plane

Ox x ; the disc strikes the

Ox -axis at the moment

t and continues to roll

MECHANICAL SYSTEMS, CLASSICAL MODELS

without sliding on this axis. Before the collision, the position of the disc depends on three

parameters: the co-ordinates

and

ρρ of the centre C of the disc and the angle of

rotation

, taken counterclockwise (Fig. 18.8). As an effect of the collision, two new

constraints are introduced: the contact with the

Ox -axis (hence =

Rρ ) and the rolling of

the disc on this axis (

Rρθ). Choosing conveniently the origin O , one introduces the

generalized co-ordinates

==−=−

1122 31

,,qq Rq Rρρ ρθ, so that the constraint

relations are expressed in the form

0, 0qq. Denoting by =

IMi the moment

of inertia of the disc with respect to the pole

O , where

i is the corresponding radius of

gyration, we can write the kinetic energy in the form

()

⎡

⎤

=++= −++

⎢

⎥

⎣

⎦

2222 22

12 13 12

TMi M qq qq

θρρ



  

We have at our disposal only a relation of the form (18.3.34''), corresponding to the

generalized co-ordinate

q , which does not vanish at the collision moment, that is

()

[]

′′ ′ ′′ ′ ′′ ′

−− − +−=

11 3 3 1

qq qq qq

   .

But

0q after collision, hence we have

′′

0q too. Returning to the old variables,

we can write

()

′′ ′ ′′ ′

−+−=

111

ρθρρ





the velocity of the centre of the disc in a rolling motion on the

Ox -axis being given by

()

′′

RR i

ρθ



(18.3.35)

′′

Riρθ



, then the disc stops.

18.3.2 Applications

In what follows we present several applications, interesting by themselves, to

illustrate the results previously obtained: the motion of a particle in various cases of

loading, the problem of two particles and the problem of two centres; as well, we

consider some cases of motion of the rigid solid: the plane motion of a bar, the double

pendulum, the sympathetic pendulums etc.

Lagrangian Mechanics

18.3.2.1 Motion of a Particle

Using the expression =++

222

123

(/2)( )Tm xxx of the kinetic energy, in case of a

single particle

P , Lagrange’s equations (18.2.29) take the form ( ==,1,2,3

qxj )

()

∂

=⋅ +⋅ =⋅δ=⋅ = = =

∂∂

F F Fi Fi

,1,2,3

jjjj

kkj

mx F Q k

txx



so that we find again the equations of motion (6.1.22').

In the case of cylindrical co-ordinates

===

123

,,qrq qzθ , the kinetic energy

(see the formula (5.1.13'')) has the form

=++

2222

(/2)( )Tm rr zθ





, resulting

Lagrange’s equations (

=++ri ii

123

cos cosrrzθθ)

()

∂

−=⋅=⋅ + =⋅==

∂

FFi iFi

(cos sin )

rrr

mr mr F Q

θθθ



 ,

()

[]

()

∂

=⋅ =⋅ − + =⋅ = =

∂

FF i iFi

(sin cos )

mr r r rF Q

θθθ



()

∂

=⋅ =⋅ = =

∂

FFi

mz F Q



being thus led to the equations of motion (6.1.26), (6.1.26'). In particular, we obtain the

plane motion in polar co-ordinates.

As well, in the case of spherical co-ordinates

===

123

,,qrq qθϕ (see the formula

(5.1.12'')), we can write

=++

222222

(/2)( sin )Tm rr rθθϕ





, while Lagrange’s

equations read (

=++ri ii

123

sincos sinsin cosrrrθϕ θϕ θ)

()

∂

−+ =⋅

∂

=⋅ + + =⋅ = =

Fi iiFi

222

123

sin

(sin cos sin sin cos ) ,

rrr

mr mr

θθϕ

θϕ θϕ θ





()

[]

()

∂

−=⋅

∂

=⋅ + − =⋅ = =

FiiiFi

22 2

123

sin cos

cos cos cos sin sin ,

mr mr

rrrFQ

θθθ

θθθϕ

θϕ θϕ θ



()

[]

()

∂

=⋅

∂

=⋅ + =⋅ = =

FiiFi

sin

sin sin sin cos ,

rrrFQ

ϕϕϕ

θϕ

θϕ θϕ



wherefrom we get the equations of motion (6.1.25), (6.1.25'). If the support of the force

pierces the

-axis, then

= 0Q

, so that we can write the first integral

sin constmr θϕ

(18.3.36)

according to which the projection of the particle

P on the plane

Ox x moves after the

law of areas.

MECHANICAL SYSTEMS, CLASSICAL MODELS

100

Analogously, we find again the equations (6.1.24''') in arbitrary curvilinear co-

ordinates.

Let be, e.g., the quadric

++−=

222

123

xxx

ααα

(18.3.37)

and the quadrics homofocal to this one

++−=

−−−

222

123

xxx

αλαλαλ

(18.3.37')

If, to fix the ideas,

123

ααα, then the equation (18.3.37') represents an ellipsoid

for

λα, an one-sheet hyperboloid if <<

αλα or a two-sheet hyperboloid if

αλα. Through each point

123

(,, )Px x x pass three homofocal quadrics

=,1,2,3

iΓ . Supposing that the co-ordinates

123

,,xxx are given, the equation

(18.3.37') of third degree in

λ has three real roots <<<<<

332211

qqqααα, as

one can easily verify; the root

q leads to a two-sheet hyperboloid, the root

q leads to

an one-sheet hyperboloid, while the root

q correspond to an ellipsoid. These three

quadrics are orthogonal two by two. We obtain thus the elliptical co-ordinates

(introduced by Jacobi)

123

,,qqq of the point

. Obviously, we have

()()()

−−−

++−=

−−−

=− − −

222

123 123

123

122

()

() ;

xxx qqq

λλλ

αλαλαλ λ

λαλαλαλ

multiplying by

αλ and making then ==,1,2,3

iλα , we can express the

Cartesian co-ordinates as functions of the elliptic co-ordinates in the form

()()()

()

−−−

=≠≠≠=

−−

123

,,,,1,2,3

iii

ji i

qqq

xijkiijk

ααα

αααα

(18.3.38)

Calculating the logarithmic derivatives, we obtain the element of arc

()

=++

2222

11 22 33

dddd

s AqAqAq

(18.3.39)

where

()()()

()

=++

−− −

−−

=≠≠≠=

222

123

222

1231

!, , ,, 1,2,3.

()

iji

xxx

qa qa qa

qqqq

ijkiijk

(18.3.39')